考虑水压作用过程的盾构隧道接缝防水机制研究

张亚洲， 冯升明， 由广明， 温竹茵

(上海市政工程设计研究总院(集团)有限公司， 上海 200092)

0 引言

随着我国城市建设的快速推进和交通需求的增加，盾构法隧道不断朝大直径、高水压方向发展[1-5]。盾构隧道由预制管片逐块、逐环拼装而成，因而管片块间及环间存在大量接缝。如上海周家嘴路隧道工程，盾构段全长2.57 km，隧道外径14.5 m，含纵缝12 860个、环缝1 286个，合计缝长8.43万m； 上海北横通道工程Ⅱ标，盾构段全长6.4 km，盾构外径15.0 m，接缝总长达21.5万m。接缝防水问题已成为制约盾构隧道技术发展的重要因素。

目前在管片接缝防水构造中，三元乙丙橡胶(EPDM)弹性密封垫是最重要的防水线。国内外对管片接缝弹性密封垫防水能力的研究主要有试验研究和数值模拟等方法。文献[6-12]结合实际工程对管片接缝弹性密封垫的防水能力开展了一字缝、T字缝防水试验和闭合压缩力试验。文献[13-15]基于不可压缩橡胶材料Mooney-Rivlin本构模型，利用数值分析软件对弹性密封垫在不同形状及不同压缩量下的变形特性、接触面应力分布及压缩力进行数值模拟分析。孙廉威[16]建立了弹性密封垫受水压作用下的数值模型，对弹性密封垫在不同张开量下的防水性能、接触应力分布以及防水失效模式进行研究，提出基于施加水压的防水性能评价方法。

目前在密封垫的试验及数值模拟研究中，认为三元乙丙橡胶弹性密封垫主要依靠橡胶密封垫的弹性压密，以接触面的表面接触应力来止水。然而，弹性密封垫粘贴于管片槽口，在盾尾拼装、脱出盾尾直至其发挥防水作用期间，水压作用过程较为复杂，这一过程对密封垫的防水能力有何影响，当前的研究并不多，部分考虑水压作用的研究仅以面力施加于密封垫表面[16]，与水体渗透的实际工况存在较大差距，且不能正确直观地表现水体渗透过程，进而得到密封垫表面应力状态。因此，本文以上述学者的研究为基础，结合密封垫拼装至发挥防水作用的动态过程，采用有限元分析软件构建流固耦合计算模型，对接缝渗流进行动态精细化模拟，并探讨密封垫的防水机制。

1 弹性密封垫水压作用过程分析

管片拼装前，弹性密封垫粘贴于管片槽口，并随管片调运下井，随着盾构的掘进，管片依次在盾尾拼装成环。由于弹性密封垫顶部表面高于管片接缝面，弹性密封垫受到千斤顶顶力(环缝)、管片自重压力产生的分力(纵缝)及螺栓紧固力的作用而发生压缩变形，如图1(a)所示，此时，在盾壳及盾尾刷的保护下，弹性密封垫未承受水压作用。

随着盾构继续掘进，开始下一环管片拼装，该环管片部分弹性密封垫暴露于盾壳及盾尾密封刷的保护之外，如图1(b)所示。此时，部分弹性密封垫将承受来自地层中的水压作用，并且水压的作用方向主要垂直于弹性密封垫的压缩方向。

随着盾构的继续掘进，该环管片完全暴露于地层中，如图1(c)所示。此时，若水压较大，密封垫防水能力不足，地下水将沿弹性密封垫之间或密封垫与管片密封垫槽之间渗入隧道。

(a)

(b)

(c)

2 CEL流固耦合计算模拟

2.1 工程概况及防水设计

上海周家嘴路越江隧道全长4.45 km，其中盾构段长2.57 km，隧道直径为14.5 m，单管双层双向4车道布置。盾构隧道最大覆土深度近45 m，隧道底部最大水压力约为0.6 MPa，是目前上海已建和在建隧道项目中覆土最深、承受水压力最大的盾构隧道[17]。隧道采用单道接缝防水体系及EPDM作为主防水材料，弹性密封垫断面如图2所示。防水设计要求为： 张开6 mm、错缝8 mm时，能长期抗1.2 MPa水压； 为了避免弹性密封垫压缩时挤坏密封垫槽外侧的混凝土，要求控制密封垫的闭合压缩力不大于60 kN/m。

图2 弹性密封垫断面 (单位： mm)

2.2 有限元计算模型

为探索在水压作用过程中防水密封受力变形状态及密封机制，在有限元软件中建立了采用欧拉-拉格朗日计算方法的流固耦合计算模型。模型中混凝土密封垫槽采用刚体进行模拟，弹性密封垫采用实体单元，水体采用欧拉单元。水体上部设置一刚体压板来压迫水体运动。弹性密封垫与混凝土密封垫槽之间采用表面对接触，密封垫自身外表面及内孔间采用自接触。接触对法向设置采用硬接触，切向设置为罚模式，参考相关数值计算[18-20]，密封垫与管片摩擦因数设定为0.5，自接触摩擦因数为0.3。水体与混凝土密封垫槽、弹性密封垫及上部压板之间设置通用接触。有限元模型及网格划分如图3所示。

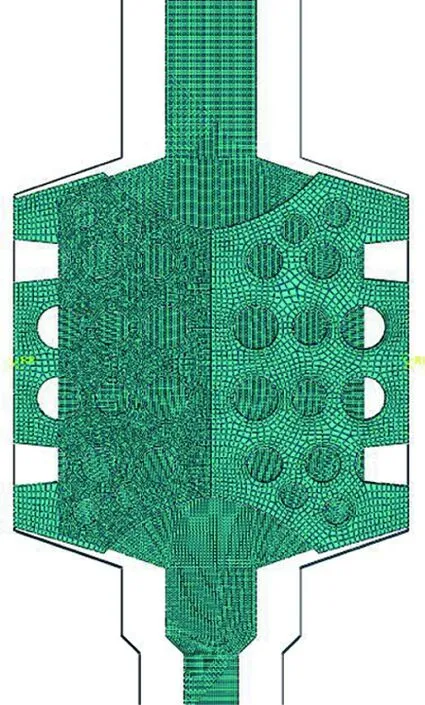
图3 有限元模型及网格划分

橡胶材料应力与应变之间的非线性关系主要通过应变能函数来定义。盾构隧道防水用三元乙丙橡胶密封垫，工程上通常采用Mooney-Rivlin模型来模拟，水体状态方程采用Us-Up，具体计算参数如表1所示。

表1 计算参数

模型初始边界条件设置为固定刚体只释放水平方向位移，固定密封垫只释放竖向及水平向位移，限制垂直欧拉区域边界面的速度为0。

本次模拟根据周家嘴路隧道工程弹性密封垫压缩力试验，两侧密封垫相对压缩量为10 mm，使双侧垫槽张开6 mm。为使模型计算稳定，10 mm分3次加载，单侧分别相对压缩1、2、2 mm。竖向水体位移采用压板控制，压板每级加载位移2 mm，直至水流突破密封垫。

2.3 计算结果分析

水体渗入过程见图4。由图4可以看出： 随着管片相对挤压，密封垫逐渐变形充满整个槽腔，随后水体进入腔内逐渐充满剩余空间，压力作用于密封垫表面，此时水体还未能突破密封垫之间的间隙，对密封垫整体进行再压缩，密封垫间的接触压力进一步增强； 当水压增大到一定程度后，水体开始楔入密封垫之间，使得密封垫上部向两侧挤压，进而使得密封垫下部的相对压缩更加紧密； 随着水压进一步增大，水体继续冲挤密封垫，最终完整突破进入内部空腔。

(a) (b) (c) (d)

提取各阶段密封垫间的平均接触应力，如图5所示。可以看出，在张开量为6 mm时，管片挤压完成后，水体的楔入使得密封垫的接触应力不断增大。在水体楔入后，平均接触应力提升了约42.5%；当水体恰好突破密封垫时，平均接触应力较水体未楔入时增大了61.25%。

图5 密封垫顶面平均接触应力变化曲线

2.4 弹性密封垫防水试验分析

周家嘴路隧道工程三元乙丙橡胶弹性密封垫经过压缩力试验、不同错台量及张开量下的一字缝及T字缝试验验证[17]，满足设计要求。为与数值分析工况对应，仅取闭合压缩力试验及0错缝情况下的一字缝试验结果进行分析。试验设备和试验过程如图6和图7所示，试验结果如图8和图9所示。

(a) 压缩试验设备

(b) 压缩试验过程

(a) 水压试验设备

(b) 一字缝试验过程

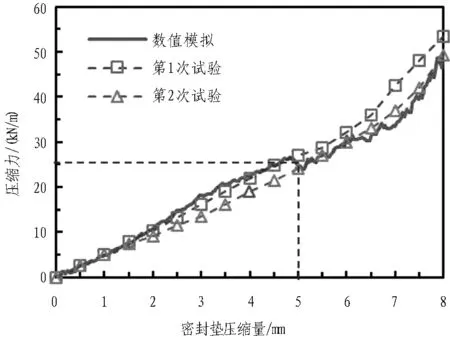
图8 弹性密封垫压缩力试验曲线

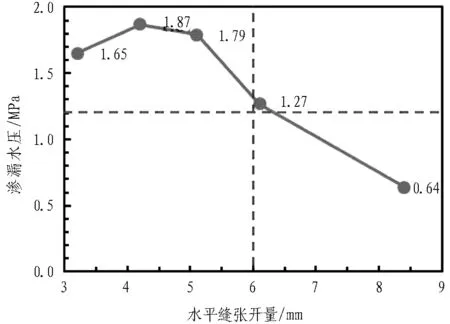
图9 弹性密封垫防水能力试验曲线

由图8可知，2次弹性密封垫压缩力试验得到的闭合压缩力分别为53.3 kN/m和49.3 kN/m，主要是由于伺服作动器读数波动导致的试验系统误差。同时，数值计算得到的闭合压缩力曲线形态与试验结果较为吻合，计算得到的最大闭合压缩力为49.8 kN/m。

此外，由于弹性密封垫最大压缩量为8 mm，张开3 mm(即与设计要求的双侧张开6 mm情况一致)相应的压缩量为5 mm，此时的压缩力为25 kN/m。密封垫顶面宽度为30 mm，可换算在无外水压作用下弹性密封垫顶面的平均接触应力约为0.83 MPa。考虑由于密封垫变形、腰部拱起引起的接触面积增大，平均接触应力应略小于0.83 MPa。这一结果与数值计算得到的管片挤压阶段密封垫顶面平均接触应力相符。

由图9可知，随着水平缝张开量的增大，渗漏水压基本呈下降趋势。在张开6 mm的情况下，密封垫的防水能力为1.27 MPa，大大高于相应张开量下的初始平均接触应力(略小于0.83 MPa)。同时，这一结果也与数值计算得到的水体突破阶段密封垫顶面平均接触应力相差不大。

2.5 考虑水压作用过程的防水机制分析

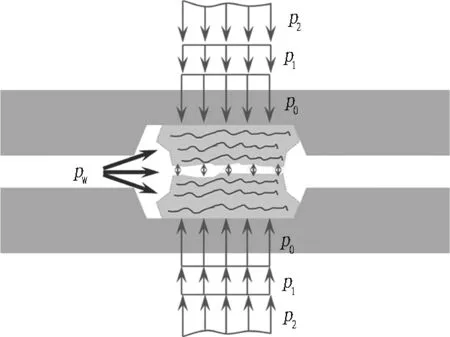
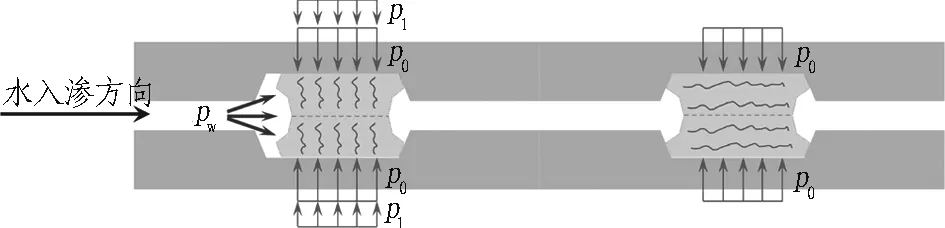
结合上述弹性密封垫水压作用过程、CEL流固耦合计算及防水试验结果，可以得到考虑水压作用过程的弹性密封垫防水机制，即管片挤压-外水推挤-水体楔入-水体突破4个阶段，如图10所示。

1)管片挤压阶段。当管片在盾尾拼装完成后，弹性橡胶密封垫被管片挤压，并且不承受外水压作用(见图1(a))，产生起始接触应力p0，这是密封垫产生防水能力的基础，如图10(a)所示。

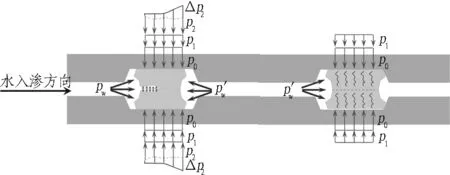
2)外水挤压阶段。当管片脱出盾尾后(见图1(b))，水体瞬时作用于密封垫迎水面一侧，使密封垫发生推挤，由于管片密封槽的限制，引起密封垫产生垂直于水压方向的应力增量p1，如图10(b)所示。需要明确的是，由于密封垫构造、底部与密封槽之间的摩擦和粘贴作用，不同情况下密封垫推挤变形形态差异较大。这时，密封垫的防水能力可以表达为p=α(p0+p1)(α为与密封垫的材质和变形特征、耦合面的表面状况等因素有关的参数)。当水压pw

3)水体楔入阶段。当外水压足够大，管片挤压、外水推挤产生的密封性能不足以抵抗水的楔入作用时，水体将会从迎水面楔入，迫使密封垫产生垂直于水楔入方向的挤压，从而进一步产生应力增量p2，且在水体楔入过程中p2处于不断增长状态，如图10(c)所示。这时，密封垫的防水能力可表达为p=α(p0+p1+p2)。当水压α(p0+p1)

4)水体突破阶段。当水压过大时，水体沿着密封垫间的接触面不断楔入，直至突破密封垫，此时由于水体楔入产生的密封垫顶面接触应力增量达到p2max，即pw>α(p0+p1+p2max)时，水体突破密封垫，发生渗漏，如图10(d)所示。

(a) 管片挤压阶段

(b) 外水推挤阶段

(c) 水体楔入阶段

(d) 水体突破阶段

3 双道弹性密封垫的防水机制探讨

接缝处的弹性密封垫可以设置单道或双道(如图11所示)。单道防水以其防水体系简单、容易找到渗漏点以及施工方便等优势，在盾构隧道中被广泛应用，如上海北横通道、诸光路通道、迎宾三路隧道、外滩通道工程等。双道防水主要是在内侧加设1道三元乙丙橡胶密封垫，近年来使用双道防水的案例逐渐增多，如上海青草沙水源地原水工程、上海苏州河深层排蓄水隧道工程、南京纬三路隧道、苏通GIL管廊等。

(a) 单道防水密封 (b) 双道防水密封

对于双道弹性密封垫，认为主要存在以下优势： 1)有助于管片拼装时受力均匀，平稳闭合。2)当发生渗漏时，可在2道密封垫之间注入止水材料，堵漏效果较好。3)适用于有内水压的隧道。4)增加防水可靠性。

然而，目前尚未明确双道弹性密封垫可靠性能提升的机制，本文基于上文考虑水压作用过程的盾构隧道接缝防水机制，分析双道弹性密封垫可靠性能提升的原因。

双道弹性密封垫防水机制示意图如图12所示。图12(a)-(d)的4个阶段是水压突破第1道密封垫的过程，这一过程与单道密封垫相同。当水突破第1道密封垫后，进入第1道与第2道密封垫之间的空腔，并逐渐充满，产生水压pw′，对第1道密封垫产生向迎水侧的挤压作用，从而使第1道密封垫接触应力产生增量Δp2，此时产生的应力增量使防水能力提升为p=α(p0+p1+p2max+Δp2)。由此可知，当外水压pw稍大于α(p0+p1+p2max)时，水体即使突破第1道弹性密封垫，也会由于Δp2的作用使其发生"自愈"，如图12(e)所示。需要明确的是，这种"自愈"作用相对有限，相较于单道弹性密封垫，双道弹性密封垫的外道弹性密封垫防水性能仅能提升10%左右。当水压较大时，Δp2不能使第1道密封垫发生"自愈"，从而导致第2道密封垫经历水体楔入、水体突破，导致密封失效。

(a) 管片挤压阶段

(b) 外水推挤阶段

(c) 水体楔入阶段

(d) 水体突破阶段

(e) "自愈"阶段

4 结论与建议

1)利用CEL流固耦合模拟能够较为直观、精细地模拟水体突破弹性密封垫的过程。

2)从管片拼装到隧道渗漏的过程中，弹性密封垫经历了管片挤压-外水推挤-水体楔入-水体突破4个阶段。

3)当水压pwα(p0+p1+p2max)时，水体突破密封垫，发生渗漏。

4)由于双道弹性密封垫之间存在储水空腔，空腔中的水压作用于第1道弹性密封垫的背水侧，能够引起第1道弹性密封垫的"自愈"，因而能够在一定程度上增加防水的可靠性。

本文仅结合无错动情况下单道防水密封垫的动态数值模拟对双道防水密封垫的工作机制进行相关探讨，而对于其产生"自愈"时的形态及各阶段压力的具体分界数值还不清晰，后续将结合错缝状态下双道防水密封垫的相关试验及数值模拟进一步探索。