弹性介质包围的球形液体腔中气泡和粒子的相互作用*

张陶然 莫润阳 胡静 陈时 王成会 郭建中

(陕西师范大学超声学重点实验室, 西安 710062)

为探究外层弹性介质对液体腔内气泡和粒子相互作用的影响, 从速度势分布理论出发, 结合拉格朗日方程得到了腔内气泡和粒子的运动方程, 分析了气泡的共振频率及声波作用下粒子和气泡间的相互作用对其平动行为的影响. 结果表明, 介质弹性和密度等特性均可改变腔内气泡的共振频率, 表现为气泡的共振频率随着球腔的半径增大有先减小后增大的变化趋势, 且逐渐趋于无界液体中单泡的共振频率. 气泡和粒子在球形液体腔中的平动受到声场参数、外层弹性介质特性、气泡和粒子本身特征等因素的影响, 总体特征表现为粒子有向腔壁运动的趋势, 气泡的平动与气泡和粒子间相互作用特征密切相关.

1 引 言

弹性介质包围的液体腔内部气泡动力学研究在地质[1]、生物学[2,3]等领域有比较广的应用. 气泡在液体中的非线性振动可引起空化效应, 形成局部高温高压和冲击波等极端现象, 在一定程度上可促进化学反应和物质交换等. 近年来, 许多学者对超声波作用下气泡的空化现象进行了广泛而深入的研究, 发展了气泡处于无界液体中[4,5]或液体内的界面附近[6]等情形下的气泡动力学. 为简化分析,在研究螺旋桨面[7,8]、血管壁[9,10]附近的气泡振动时近似将界面简化为无限大硬壁面后, 借助于镜像理论等研究气泡与界面间的相互作用. 在生物学中, 液体中微泡运动通常受到血管或软介质的约束, 因此, 血管内气泡的动力学行为的研究对分析空化气泡的生物学影响尤为重要. 在特定的环境中, 液体可能存在于封闭腔体内, 当液体空化时,空化气泡的振动行为将呈现出不一样的特征.Wang[11]和Doinikov[12]等的理论研究表明弹性介质中一定大小的球形液体腔内气泡的共振频率随着气泡半径的增大而增大, 与在无界液体中气泡振动的自然频率的变化趋势完全相反, Vincent 等[13]通过实验得出弹性介质中气泡由于约束作用呈现快速振荡的运动趋势. 这预示着球形液体腔周围介质的特性将对气泡的动力学行为形成显著影响.

Rayleigh 为解释螺旋桨的空化腐蚀现象, 最早建立了不可压缩液体内气泡动力学的理论模型, 定性地分析了空化产生的机理, 为以后的空化研究奠定了基础. 在此基础上考虑液体压缩性、黏性及表面张力后对其修正得到R-P 方程, Keller 等[14]考虑声辐射、黏性、表明张力和声波的影响对气泡动力学进行了研究. 由于液体中的气泡大多以多气泡的形式存在, 人们利用牛顿力学和分析力学处理动力学问题的手段提出了两个和多个气泡间相互作用的理论模型, 如Doinikov[15]构建了两气泡体系的拉格朗日函数并结合拉格朗日方程得到了气泡径向和平动的动力学方程, Ilinskii 等[16]研究了考虑气泡间相互作用后的耦合声辐射, 以及通过构建系统哈密顿函数结合正则方程得到气泡径向振动和平动的动力学方程. 王成会等[17]考虑了气泡间次级声辐射的影响, 探讨了气泡的径向振动和平动规律. 为了解释冲击波碎石术中肾结石碎片和空化团簇的作用, 发展了无界液体中气泡和粒子相互作用的模型. Hay 等[18]在模型中假设气泡和粒子都可以自由移动并精确到五阶来描述气泡-粒子的相互作用. Li 等[19]利用边界积分法和实验研究了气泡和悬浮球之间的相互作用. 超声波作用下液体中的气泡和悬浮颗粒物等均可能与附近的空泡产生相互作用并形成空化影响, 因此, 人们发展了无界液体中粒子与气泡的运动模型. 然而, 在超声萃取或者干燥等过程中, 可能存在生物组织(弹性体)包围的液体腔内的空化行为以及空化泡与粒子间的相互作用. 因此, 有必要发展受限条件下空化气泡和粒子间的相互作用的动力学模型, 为解释超声促进物质交换等奠定理论基础. 现有的理论和实验研究表明[11,13], 负压或者声波作用下, 弹性介质包围的封闭液体腔内的气泡可生长并振荡, 其动力学行为将影响周围介质的力学性能等. 事实上, 包裹液体腔的介质也会影响腔内气泡的平动, 而密闭液体腔内的多泡体系或者粒子的存在也会影响气泡径向振动和平动行为, 为探索密闭腔内液体中气泡和粒子间的相互作用, 本文将发展气泡-粒子系统的动力学方程, 并分析气泡和粒子的平动特征.

2 理论推导

为探究弹性介质包围的液体腔内气泡和粒子的动力学行为, 从气泡、粒子及液体腔三者的速度势分布函数出发, 借助坐标变换得到速度分布及系统的动能和势能表达式, 进一步基于拉格朗日方程导出气泡和粒子的动力学方程.

2.1 速度势函数

如图1 所示, 气泡和粒子位于由弹性介质包裹的球形液腔内. 为简化分析, 假定二者在运动过程中始终保持球形, 且二者球心均位于直径z轴上,相对位置坐标为zj(j= 1, 2); 以球腔中心为坐标原点, 建立球坐标系(r,θ,φ) ; 分别以气泡和粒子中心为坐标原点建立局部球坐标系(rj,θj,φj) . 若腔内充满理想液体, 则其运动将满足拉普拉斯方程Δφ=0 , 其中φ为标量速度势.

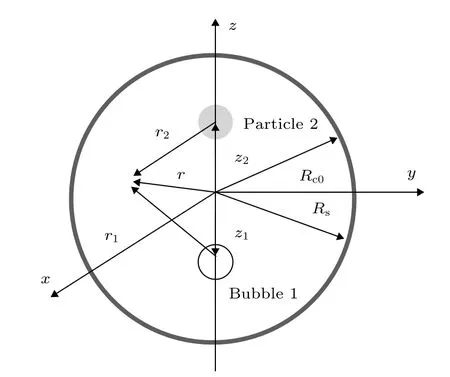
图1 充满液体的空腔中的气泡和粒子Fig. 1. The bubble and particle in a liquid-filled cavity.

液体速度势可表示为

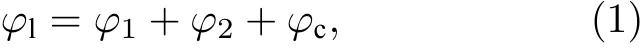
式中,φ1和φ2分别为与气泡和粒子运动相关的液体速度势,φc为腔内壁面运动相关的液体速度势;求解拉普拉斯方程, 有

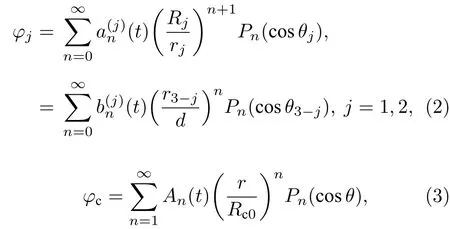
式中,Rj是为瞬时气泡(粒子)半径,Rc0是静止时空腔的半径,Pn是n阶勒让德多项式,b(nj)(t) 是与时间相关的函数,b(nj)可表示为[20]

式中ξj=Rj/d,d(t)=z2(t)-z1(t) 是气泡 与粒子中心的距离 .

为在气泡、粒子及球腔表面应用边界条件, 需将速度势φj及φc的表达式进行坐标变换. 在球腔中心为坐标原点的球坐标系中, 速度势φj为[20]

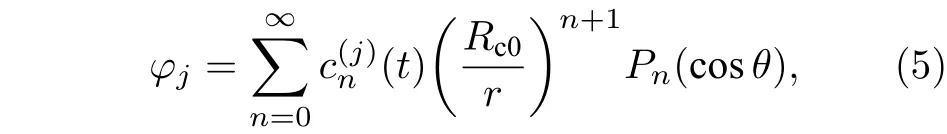
式中

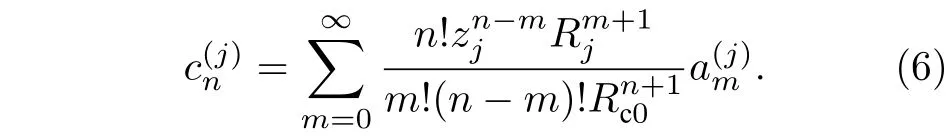
在以气泡和粒子中心为坐标原点的局部坐标系中, 速度势φc表示为[20]

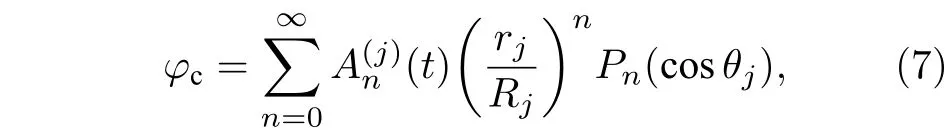
式中

气泡和粒子表面法向速度对应的边界条件为

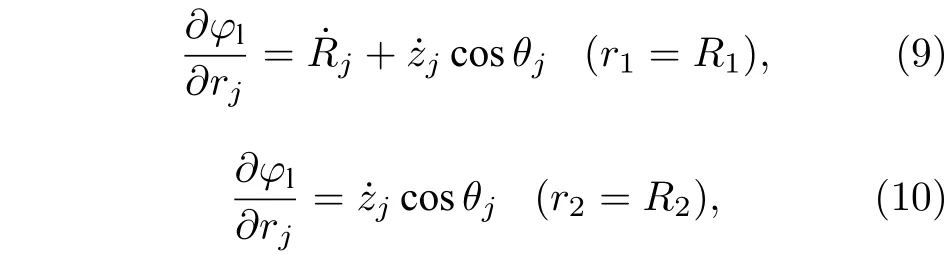
得

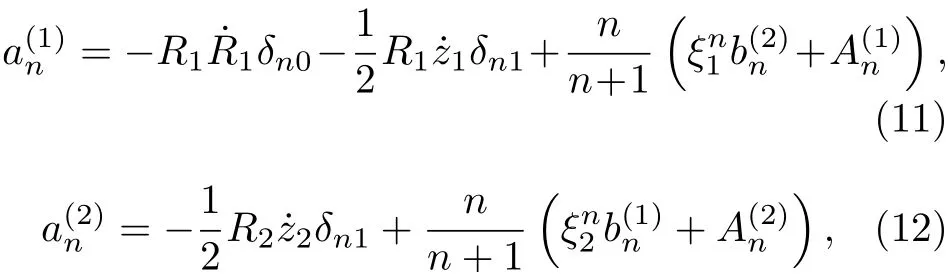
由于腔体外侧弹性介质层仅发生微小形变, 故腔内表面法向速度关系近似为

式中Rc(t) 是空腔的瞬时半径. 将(3)式和(7)式代入(13)式, 得

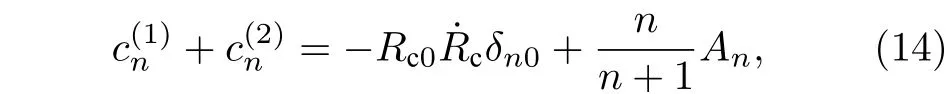
将(8)式代入(14)式中, 得

由于液体具有不可压缩性, 故液体体积守恒, 有

基于速度势分布以及边界条件可得到气泡周围介质中速度分布, 进而可以求气泡径向振动和平动过程中引起的系统动能变化, 其推导过程参见附录.

2.2 气泡和粒子的运动方程

基于拉格朗日方程可以求得径向振动气泡和粒子平动动力学方程. 系统拉格朗日函数L=T -U,其中T和U是系统的动能和势能. 系统动能包括:腔内液体动能Tl、刚性粒子平动动能Tp和弹性介质层动能Ts, 即T=Tl+Tp+Ts. 由附录知腔体内液体动能可近似表示为

粒子的动能为[21]

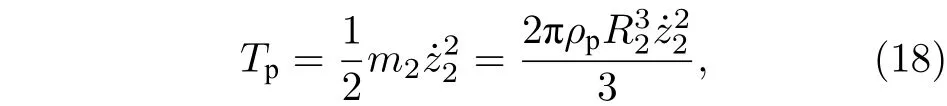
式中,ρl为液体的密度,Vl为液体所占体积,ρp为粒子的密度.

空腔外分布有球壳状弹性介质层, 其壳层内外半径分布为Rc0和Rs. 由于液体不可压缩, 空腔内气泡的径向体积脉动必然引起弹性壳层的运动, 其动能可以表示为[20]

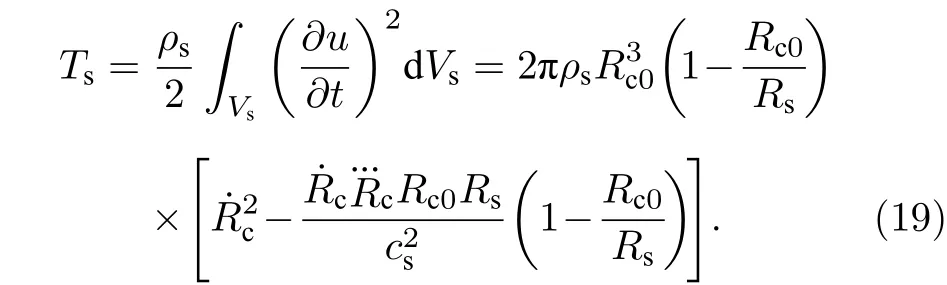
式中ρs为固体的密度. 系统势能包括气泡体积势能和腔壁外层介质弹性势能, 即U=U1+U2, 其中U1可表示为[21]

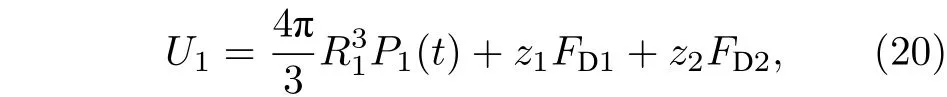
式中P1(t) 是气泡表面的压力,FDj是气泡和粒子所受的黏性阻力, 在液体势能表达式中加入气泡和粒子在平动时受到黏性阻力相关的项; 声压P1和黏滞力可以表示为[21]:

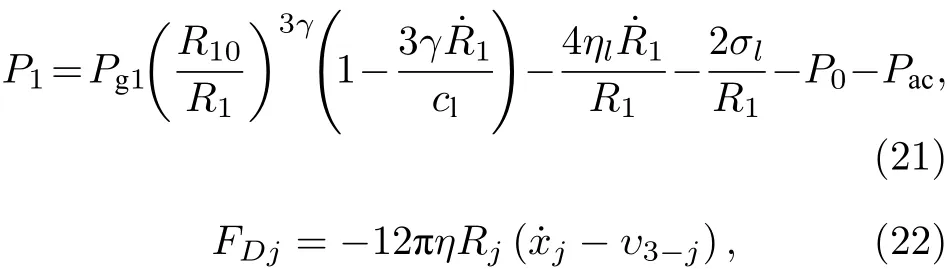
式中Pg1=P0+2σl/R10是气泡内部的平衡蒸气压;R10是气泡1 的平衡半径;cl是液体中的声速;γ是液体的比热;σl是表面张力;ηl是液体的黏度;P0是液体中的静态压力;Pac是驱动声压;f是声波频率;N是循环数, 其取值决定高斯波的作用时间;υj表示气泡(粒子)所在位置与彼此相互作用有关的液体体元振速, 其表达式为[15]

需要特别说明的是, 对粒子(j= 2), 在 (23)式中有=0 .

空腔外弹性介质层的势能Us可表示为[20]

式中µ为固体的剪切模量.

将动能表达式(17)式—(19)式和势能表达式(20)式和(24)式代入拉格朗日方程

可得密闭球形液体腔内气泡和粒子的动力学方程分别为:

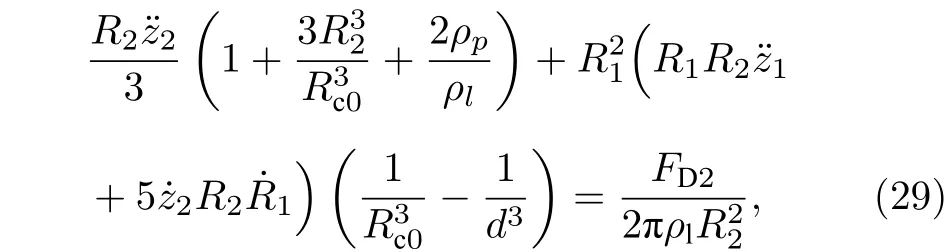
式中

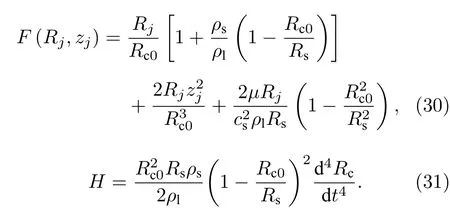
动力学方程(27)中出现了腔壁瞬时半径Rc对时间的高阶倒数, 根据液体体积不变, 结合(16)式和(27)式, 约去高阶小量, 近似有

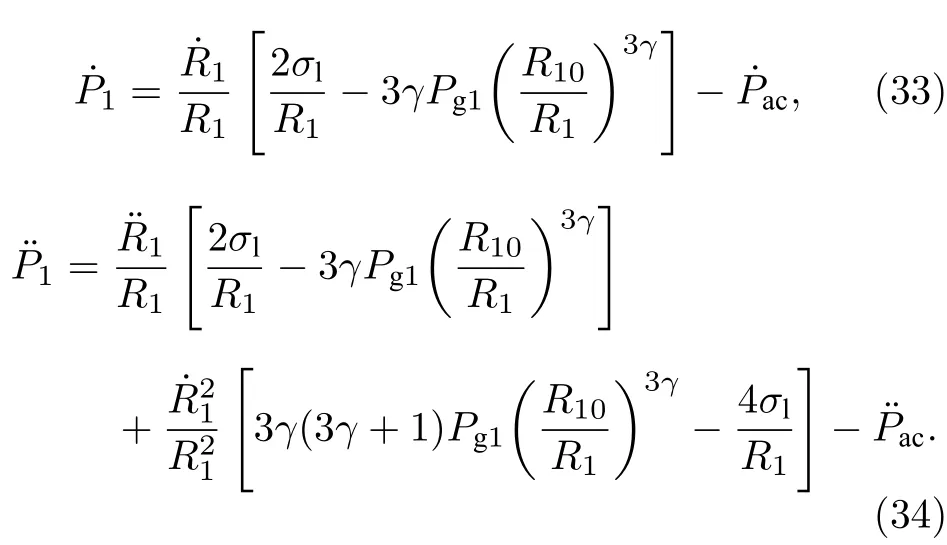
2.3 球腔内气泡的共振频率

为分析密闭腔内气泡相对位置对气泡共振频率的影响, 设

且有|x1|≤R10,|xc|≤Rc0, 若腔外侧介质厚度趋于无穷, 即Rs≫Rc0, 忽略(26)式展开式中的高阶小量, 可得到气泡线性振动方程, 即

其中

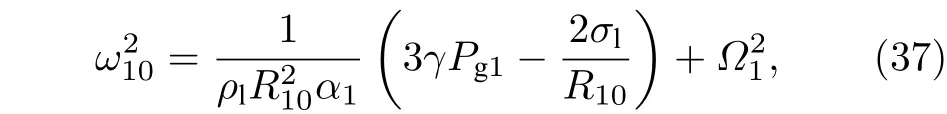
由此可以看出, 球腔内气泡的共振频率与腔外介质密度、弹性、液体表面张力系数、环境压力及气泡在球腔内的位置等因素有关.

3 数值分析

基于密闭腔体中液体内气泡和粒子间的相互作用相关的动力学方程(27)式—(29)式可分析气泡的径向振动和平动以及粒子的平动, 采用的参数有:ρl=1000 kg/m3,cl=1500 m/s ,ηl=0.001 Pa·s ,σl=0.072 N/m,ρs=1233 kg/m3,cs=2111 m/s ,γ=1.4 ,µ=6 MPa ,f=0.7 MHz ,P0=101.3 kPa ,Pa=2 atm (1 atm = 101325 Pa),R1=R2=5 μm ,ρp=1.5ρ,Rc0=500 μm,Rs=Rc0+500 μm,d=10 μm,N= 10. 空腔外弹性介质层设为水凝胶[20].

Wang[11]分析了介质体积弹性对弹性介质包围的液体腔中心的气泡的共振频率的影响, 发现随着液体腔半径与气泡半径比值增大共振频率逐渐减小并趋近于无界液体中单气泡共振频率. 为更清楚地认识液体腔周围介质对气泡共振频率的影响,基于(37)式我们分析R10= 2 µm 的气泡的相对共振频率ω10/ωm随半径比Rc0/R10的变化 (ωm是无界液体中单气泡固有频率), 如图2 所示, 其中气泡相对位置z1/Rc0分别为0, 0.3, 0.5, 对比发现相对位置对气泡的共振频率的影响较小, 几乎可以忽略不计. 随着半径比Rc0/R10的增加, 气泡的共振频率有先减小后增大的变化趋势, 在半径比7 附近存在极小值. 当半径比较小时(大约Rc0/R10< 4),气泡相对频率比大于1, 而后相对频率比小于1 且随着液体腔半径的增大逐渐趋近于1, 与Wang[11]预测结果存在一定的差异, 主要原因在于其未计入外层介质密度的影响. 从密闭腔内液体中气泡的共振频率表达式可以看出, 腔外介质的弹性的存在可使得共振频率增加, 然后随着半径比的增加, 介质弹性对共振频率的影响将逐渐减弱, 外层介质密度对共振频率的影响逐渐占主导地位, 进而导致共振频率比小于1. 随着腔体半径的进一步增大, 腔壁外侧介质特性对气泡的影响逐渐减弱, 气泡的共振频率趋近于液体中自由泡的共振频率. 因此, 液体腔外层介质对气泡的振动行为的影响会随着腔体尺寸的变化而不同.

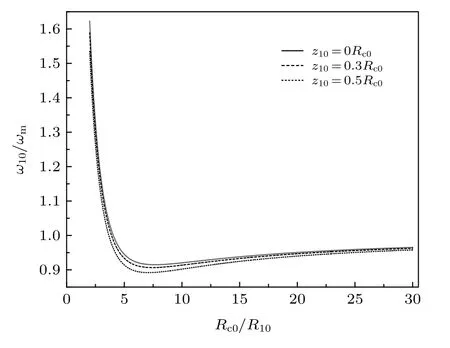
图2 相对频率随空腔半径与气泡半径比值的变化Fig. 2. The relative frequency changes with the ratio of cavity radius to bubble radius.

气泡的初始半径不同, 声场中气泡的振动行为也不同. 为分析气泡半径对粒子和气泡系统平动的影响, 选取初始半径分别为2, 3, 4, 5 µm 气泡做数值分析, 如图3 所示. 在气泡和粒子中心间距不变的条件下, 当气泡半径为2 µm 时, 气泡和粒子均向腔壁平动; 随着气泡半径的增大, 气泡向液体腔中心跳跃式平动而粒子向腔壁运动且其路径有起伏跳跃特征, 且在气泡半径为4 µm 时相互作用力最强. Wu 等[21]发现无界液体中气泡和粒子间相互作用强弱与气泡的初始半径相关并表现为互相吸引. 由于液体腔外层的弹性介质会对气泡与粒子间相互作用产生影响, 从而使得液体腔中的气泡和粒子与无界液体中的气泡和粒子的运动趋势不同,并在气泡半径不同时表现出相互吸引或排斥的特征.

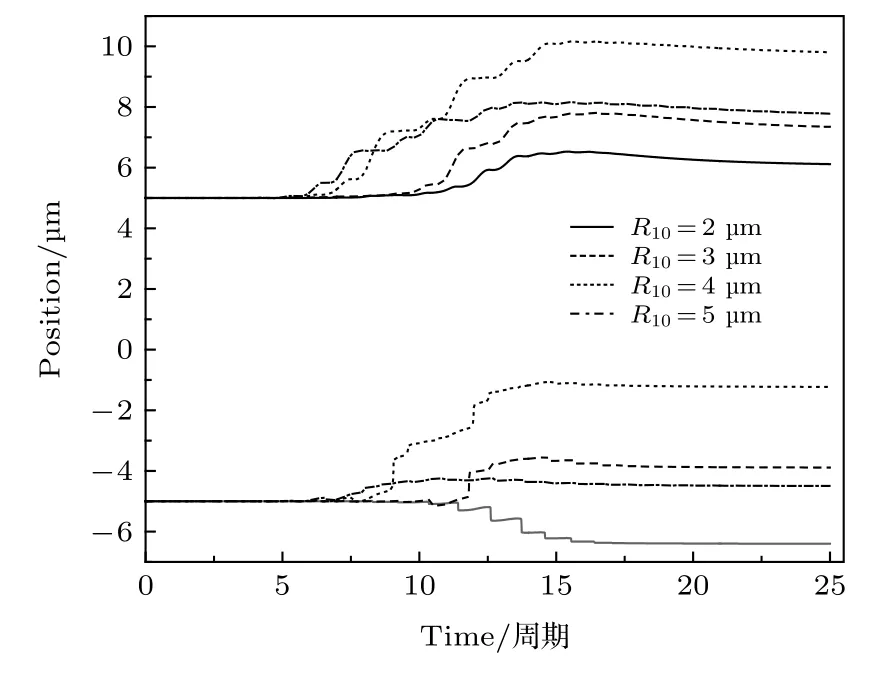
图3 气泡初始半径对气泡和粒子的平动的影响Fig. 3. The effect of initial radius of bubble on the translation of bubble and particle.

液体腔体内气泡和粒子动力学模型可用于分析超声植物提取、生物组织空化等, 应用领域不同, 选用的声波频率范围不同. 为探索频率的影响, 利用(37)式计算了5 µm 气泡的共振频率约为0.72 MHz并选取频率分别为0.7, 1.0, 1.5 MHz 的声波分析液体腔内气泡和粒子的平动, 如图4 所示. 当频率为0.7 MHz 接近气泡的共振频率时, 气泡和粒子间相互作用最强, 且表现为气泡向腔中心平动, 而粒子向腔壁运动. 随着频率的增加, 气泡的径向振动行为相对逐渐减弱, 二者之间的相互作用也减弱, 在驱动声波频率为1.5 MHz 时, 气泡和粒子间仅有轻微的相互远离运动特征.

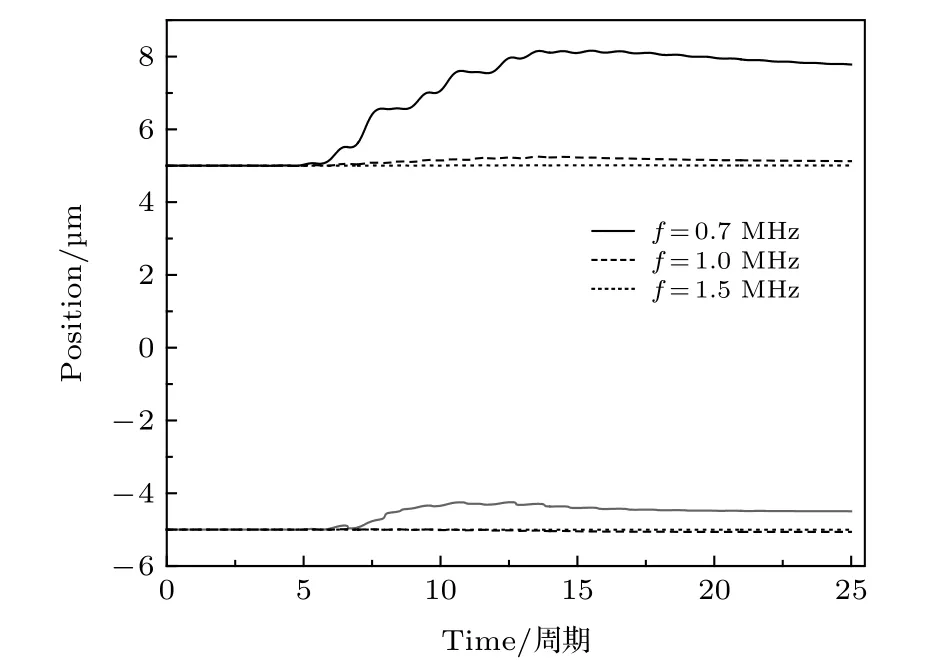
图4 驱动声波频率对气泡和粒子的平动的影响Fig. 4. The influence of driving sound frequency on the translation of bubble and particle.

声波频率一定时, 驱动声压大小决定气泡振动强弱, 进而影响气泡与粒子的平动特征, 图5 中曲线对应声压幅值分别为0.5, 1.0, 1.5, 3.0 atm. 在同样的声场条件下, 粒子相较气泡而言其平动更显著, 主要原因在于气泡的膨胀推动粒子向腔壁运动. 随着驱动声压幅值的增加, 气泡的径向振动越强, 推动粒子向腔壁运动的位移越大. 在声压幅值小于1.5 atm 时气泡进发生较小的平动位移, 而当声压幅值增大到3.0 atm 时, 气泡向液体腔中心运动. Vincent 等[13]在实验中观察到凝胶中的液体腔内气泡由于外层弹性介质的影响将向中心位置运动, 而在声波作用下, 气泡和粒子间的相互作用在一定程度上能够平衡外层弹性介质的影响, 但当驱动声压较高时, 二者相互作用增强, 将表现为更为复杂的相互吸引和排斥的特征.

液体腔的大小对密闭腔内气泡的运动状态有着显著影响, 为更进一步分析影响特征, 改变内腔半径分别为100, 300, 500 µm 分析粒子和气泡的平动, 如图6 所示. 在不同尺度的液体腔内的粒子和气泡在声波作用下的运动行为表现为: 粒子朝腔壁运动且随着内腔半径的增大粒子的运动位移变大; 对于气泡而言, 在内腔半径较小时, 外层弹性介质对气泡的振动行为的影响更为显著, 因此, 在一定程度影响可调节粒子和气泡相互吸引或排斥的状态, 表现为腔内径100 µm 时气泡向着腔壁远离粒子运动; 随着内腔半径的增大, 粒子向腔壁运动的位移变大, 声波作用下气泡则朝向球腔中心有小的位移变化.

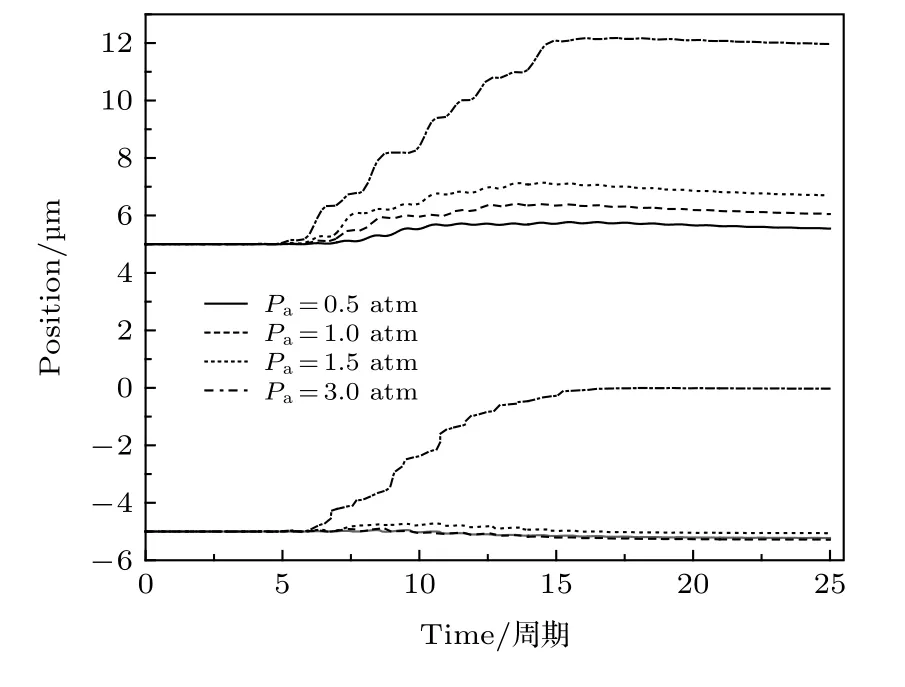
图5 驱动声压幅值对气泡和粒子的平动的影响Fig. 5. The influence of sound pressure amplitude on the translation of bubble and particle.

图6 腔体大小对气泡和粒子平动的影响Fig. 6. The influence of cavity size on the translation of bubble and particle.

液体腔内由于粒子的存在影响气泡的径向振动和平动. 为更进一步分析粒子密度对密闭腔内气泡的运动状态的影响, 比较粒子密度ρp分别为0.5ρ,ρ和1.5ρ时粒子和气泡的平动状态变化, 如图7 所示. 随着粒子密度的增大, 粒子向腔壁运动的位移逐渐减小,原因在于重粒子平动状态发生变化需要更大的推力作用.对气泡而言,粒子密度越大气泡向着球腔中心运动位移也越小,因此气泡和粒子间的相互作用同时影响二者的平动行为.

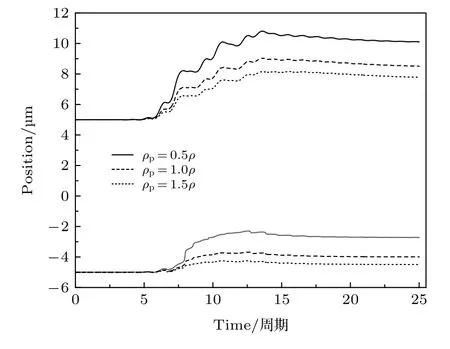
图7 粒子密度对气泡和粒子平动的影响Fig.7.The influence of particle density on the translation of bubble and particle.

4 结 论

本文构建了弹性介质包裹的液体球腔内粒子和气泡间的相互作用动力学模型,基于拉格朗日方程得到了表征气泡径向振动和平动、粒子平动动力学方程.基于此方程,可分析声场参数、球腔约束条件(如腔体大小)、气泡和粒子本身特征等因素对系统运动的影响.球形液体腔外层介质的弹性、密度、腔体结构等均可影响气泡的共振频率,由于介质弹性的影响,当气泡半径与球腔半径比较接近时,气泡共振频率大于无界液体中的共振频率;随着球腔半径的增加,气泡共振频率逐渐减小到低于无界液体中的共振频率的情形.由于气泡的径向振动形成次级声辐射引发粒子和气泡间的相互作用,进而影响二者在液体腔内的平动.气泡的径向振动可推动粒子向着腔壁运动,且气泡的振动越强,粒子在声波持续时间内的平动位移越大,同样,气泡的平动也会受到二者相互作用的调制,在不同的相互作用情形下存在向球腔中心运动和向腔壁运动两种情形.

气泡在球状液体腔内的运动可改变液体内的速度场分布,同时影响周围的物质运动状态.气泡和粒子间的相互作用在一定程度上可调控气泡的运动行为,进而增强液体腔内外物质交换,可为解释超声植物有效成分提取及生物组织内的空化行为提供理论基础.

附 录

为了得到空腔中液体的动能表达式,需要利用前文求得的液体运动的解进行推导.腔内液体动能可表示为

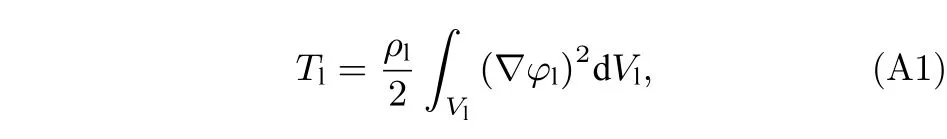
式中,ρl为与液体的密度,Vl为液体所占体积.根据变换关系,(A 1)式可进一步表示为

式中,Sc,S1,S2分别表示空腔、气泡和粒子的表面;nc,n1,n2分别表示垂直于空腔、气泡和粒子表面并指向液体的单位向量.结合(2)式—(15)式后液体速度势(1)式代入(A2)式,得

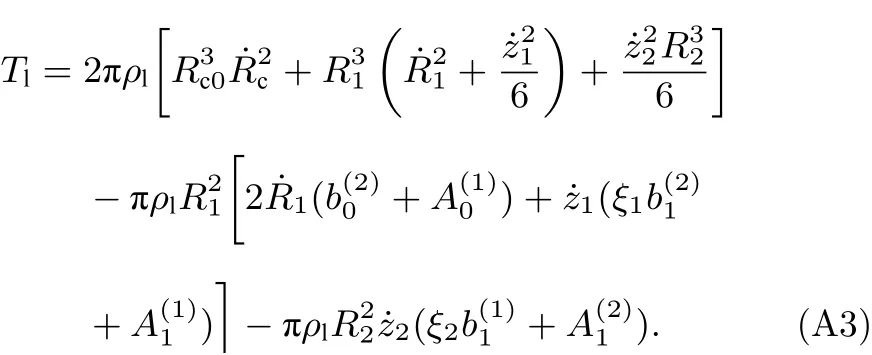
将(11)式、(12)式代入(A 3)式,液体动能的具体表达式为