中间测量对受驱单量子比特统计复杂度的影响*
巩龙延 杨慧 赵生妹
1) (南京邮电大学理学院, 江苏省新能源技术工程实验室, 南京 210003)
2) (南京邮电大学信号处理与传输研究院, 南京 210003)
最近, 基于量子信息理论的统计复杂度引起了人们的关注. 在噪声环境下, 一个受外界驱动的单量子比特系统具有丰富的动力学行为. 本文利用Lindblad 方程, 在Born-Markov 近似下, 研究 N 次中间量子测量后,在系统演化的最后时刻 τ , 末态的统计复杂度 C . 研究发现: 在 τ 由0 变大的过程中, C 从0 开始, 先增大到最大值, 然后减小, 直到再趋近于0; N 较小时, C 伴随着明显的不规则振荡现象, 振幅随 τ 逐渐减小; N 越大,C 随 τ 的变化趋势越接近无中间测量时的变化趋势. 研究结果给量子态的操控提供了一定的理论参考.
1 引 言
多年来, 系统的复杂性相关研究在物理学、化学、生物学、数学、计算机科学等领域引起了人们的广泛关注[1]. 算法复杂性、计算复杂性、生物复杂性、生态复杂性、演化复杂性、发育复杂性、语法复杂性、经济复杂性、社会复杂性等概念被提出[2].以爱因斯坦为代表的许多科学家认为自然界的基本规律是简单的, 然而物质世界呈现在人们面前是层次化、复杂化的[3]. 简单的定律多次重复应用, 在自然界中可以呈现出丰富的结构和复杂的现象[4].高维度的物理过程, 若从低维空间描述, 会使它们看起来复杂; 选取不合适的参考系也可能带来描述的复杂化[2,5].
对系统复杂性特征的刻画, 是一个脱离主观评价去定义某种可观测对象的问题[2]. 由于复杂性具有多样性, 这是一个语境依赖概念[1], 目前科学界对它没有统一的认识. 复杂性的测度, 即复杂度,有诸多定义[1]. 如基于信息学理论, 1965 年Kolmogorov[6]最早提出基于序列比特数的复杂性测度;在此基础上, 1976 年Lemple 和Ziv[7]给出具体算法, 并被称为Lemple-Ziv 复杂度; 1995 年, 基于Shannon 熵和失衡( d isequilibrium )度, López-Ruíz等[8]提出统计复杂度, 简称为LMC 复杂度; 1999 年,基于Boltzmann-Gibbs-Shannon 熵, Shiner 等[9]提出可以区分有序和无序程度的复杂度, 简称为SDL 复杂度. 2020 年, Cesário 等[10]基于LMC 统计复杂度及量子信息理论, 提出量子统计复杂度,用来研究量子相变.
另一方面, 随着实验技术的发展, 人们可以对单量子态进行操控, 探测其物理性质, 促进了量子信息处理技术的发展和应用[11]. 最近, 一个受外界驱动的单量子比特系统引起人们广泛研究[12−15].在噪声环境下, 可以通过调节外界驱动强度来操控系统的量子性特征[12−14]. 赵小新[15]详细讨论了存在多次中间量子测量时系统的量子性特征. 实际上, 通过量子测量可以从系统中提取信息、改变系统的状态[16]; 多次测量可以模拟环境对量子系统的影响[17]; 多次测量也可以用来操控、监控量子系统[18,19]. 众所周知, 简单的系统也可以表现出复杂的动力学行为. 在噪声环境下, 受外界驱动的单量子比特系统是一个典型的例子[12−14], 而多次中间测量使得该系统的动力学行为变得更加丰富[15].本文的目的, 是借助于复杂度概念对该系统的动力学行为进行定量刻画. 为此, 基于Cesário 等[10]提出的量子统计复杂度, 在不同的外界驱动强度和退相噪声强度作用下, 在多次中间测量影响下, 研究在系统演化的最后时刻τ, 末态的量子统计复杂度C.结果表明当τ由零变大, 复杂度从零开始, 先增加后减小, 直到再趋近于零; 测量次数较小或较大时,复杂度随τ的变化规律有较大差异. 这些结果有利于人们对这样的量子比特进行操控、监控等量子信息处理.
本文剩余部分安排如下: 第2 节给出统计复杂度的公式; 第3 节介绍模型; 第4 节详细讨论多次测量对量子统计复杂度的影响; 最后, 第5 节给出主要结论.
2 统计复杂度
为了不引起混淆, 经典系统和量子的统计复杂度分别被称为经典统计复杂度和量子统计复杂度.
2.1 经典统计复杂度
设某物理量有x1,x2,··· ,xK共K个可能的值,它 们的 概率 分别 为p1,p2,··· ,pK.记概率矢量p=(p1,p2,··· ,pK), 特别是记同分布概率矢量pI=(1/K,1/K,··· ,1/K). 经典统计复杂度正比于香农熵和失衡度[1,8,10]. 定义约化香农熵
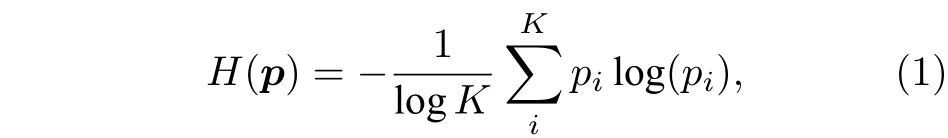
以及约化失衡度[10]
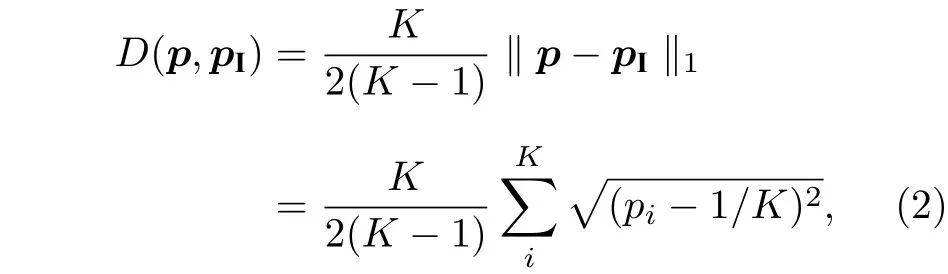
则经典统计复杂度可表示成
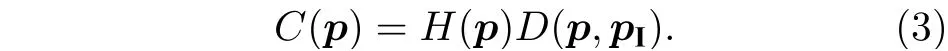
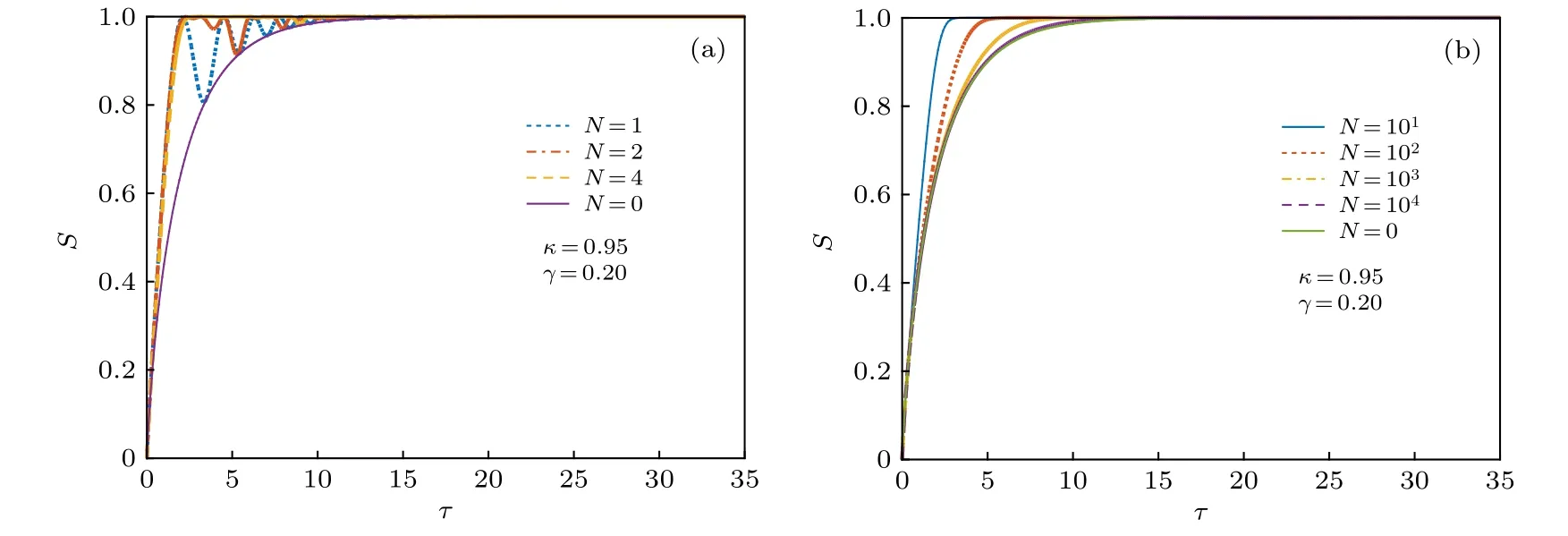
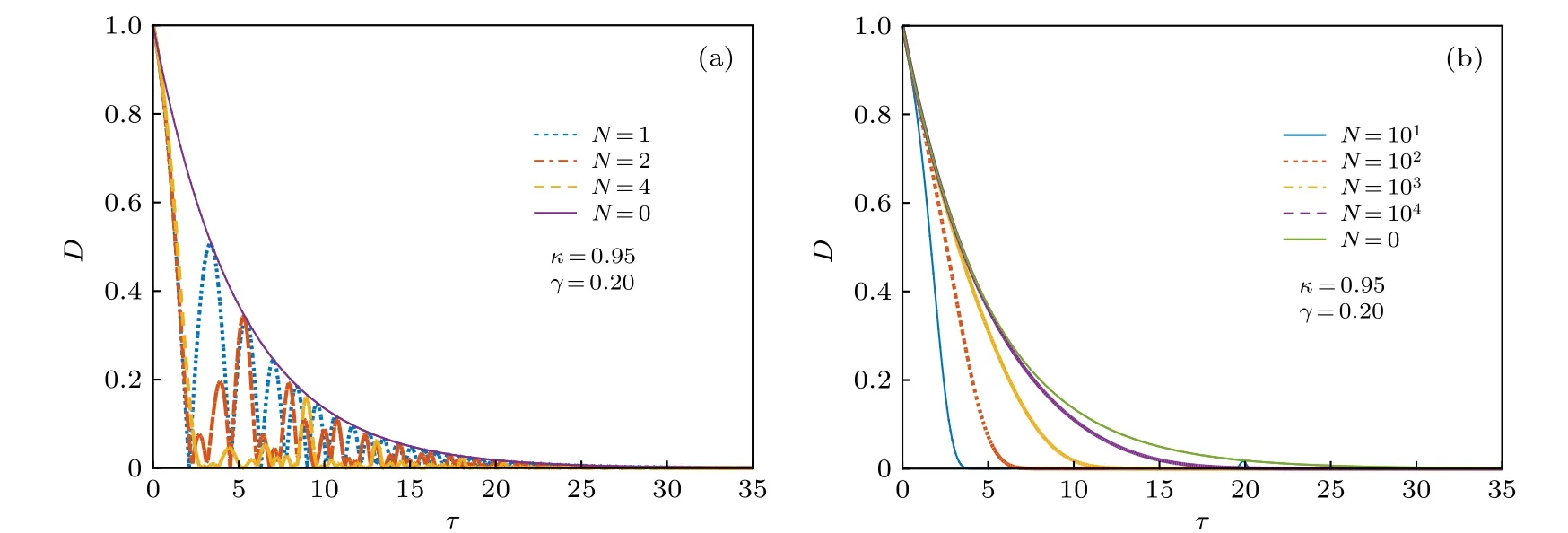
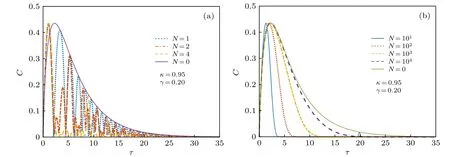
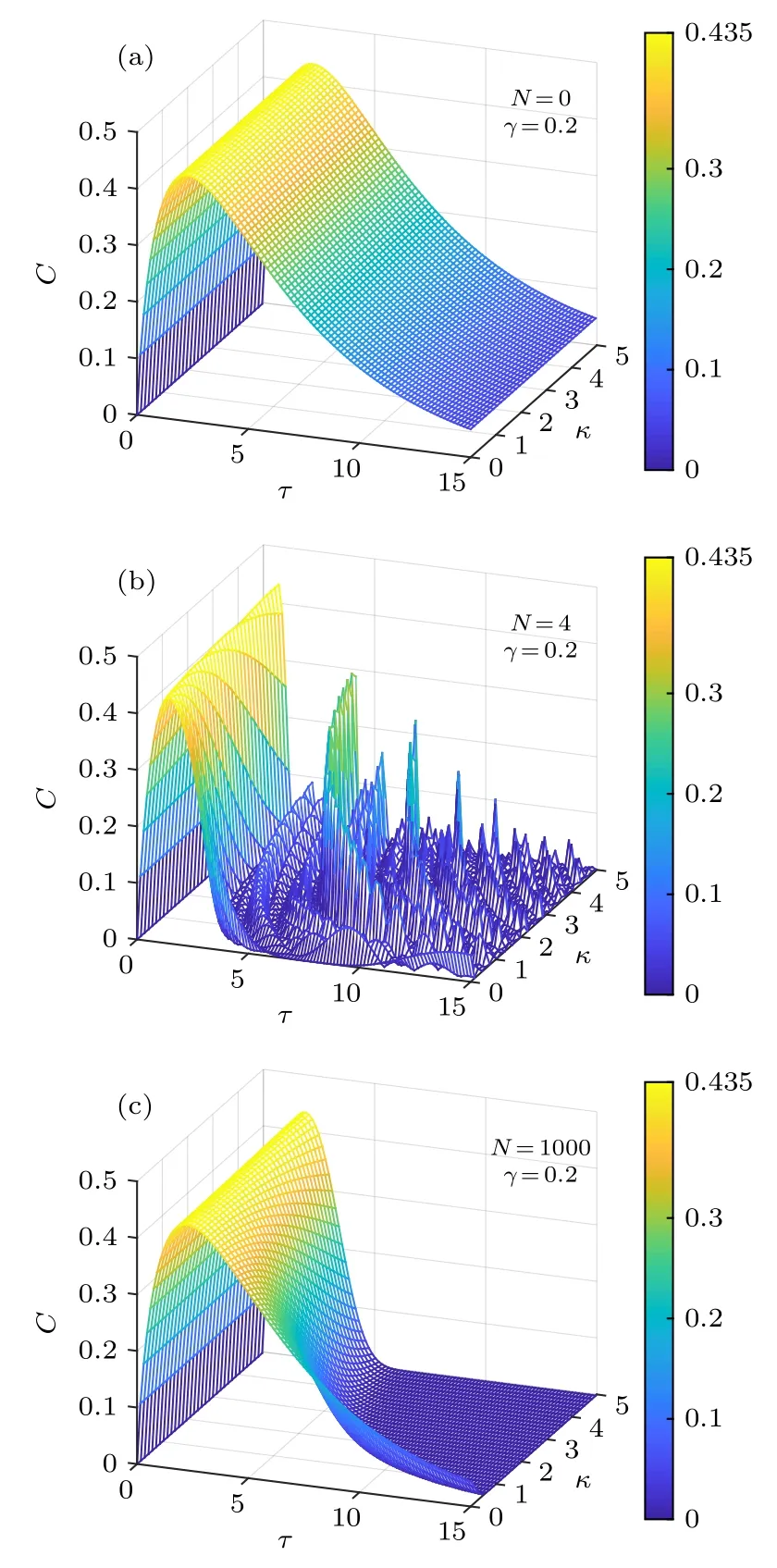
对最无序情形, 即同分布概率矢量pI, 约化香农熵H(p)=1,约化失衡度D(p,pI)=0 ; 对最有序情形, 即概率矢量p=(0,··· ,0,pi=1,0,··· ,0) ,约化香农熵H(p)=0,约化失衡度D(p,pI)=1 . 可见, 约化香农熵H(p) 可较好地表征无序程度, 而约化失衡度D(p,pI) 可较好地表征有序程度[8,10]. 在这两种极端情形下, 经典统计复杂度C(p)=0 , 而在其他情形, 0 将以上概念推广到量子系统[10], 量子态对应的密度算符ρ代替概率矢量p. 定义约化冯·诺依曼熵 以及约化失衡度 则量子统计复杂度可表示为[10] 其中约化冯·诺依曼熵S(ρ) 代替(3)式中的约化香农熵H(p),I=I/K为最大混合态密度算符,K是量子态的希尔伯特空间维度, I 是维度为K的单位算符. 最无序的量子系统对应最大混合态I, 约化冯·诺依曼熵S(I)=1 , 约化失衡度D(I,I)=0 ; 最有序的量子系统对应纯态, 其密度算符ρ=|ψ〉〈ψ|,约化冯·诺依曼熵S(I)=0 , 约化失衡度D(I,I)=1 .在这两种极端情形下, 量子复杂度C(ρ)=0 , 而在其他情形, 0 下面将分别介绍受驱单量子比特系统及多次中间量子测量. 考虑的量子比特为受外界驱动的两能级系统[12−15], 其含时哈密顿量为 其中σz为泡利算符z分量, 频率ω(t)=ω0+κt, 不失一般性, 取ω0=1,κ为外界驱动强度. 周围环境对量子系统的影响, 可用Markov 和non-Markov过程来近似. 前者用来模拟系统与环境处于弱耦合状态, 环境的记忆效应可以忽略, 系统主方程呈现Lindblad 形式; 后者用来模拟系统与环境处于强耦合状态, 环境的记忆效应不能忽略, 系统与环境间存在能量和信息的交流, 动力学演化过程更加复杂. 为了重点突出量子测量的作用, 同时弱化其他因素的影响, 本文只考虑Markov 过程近似情形. 在Born-Markov近似下,任意算符X(t) 的Lindblad 方程可表示成 其 中L为Liouvillian 超算符,γ是退相位噪声强度, 这里普朗克常数取为自然单位. Lindblad 方程用矩阵表示为 从(9)式可以看出,σz和单位算符 I 不随时间发生变化, 为简单起见, 算符X(t) 可用泡利算符σx和σy来表示, 若定义传播子 那么[13] 其中θ1=γ(t2-t1)和 如同文献[13], 在t=0 时刻, 量子比特处在σx的本征态|+〉上, 密度算符为 在随时间演化过程中, 以{σx,σy}为基, 若无中间测量, 根据(11)式 在时刻t=τ1,··· ,τn,··· ,τN, 分别进行σx(t) 测量[15],这些算符σx(τ1),··· ,σx(τn),··· ,σx(τN) 是非对易的. 以{σx,σy}为基, 算符σx可用矩阵表示[13]. 设初始时刻t=0 和系统演化的最后时刻t=τ, 那么[15] 本文研究均匀时间间隔测量对量子统计复杂度的影响, 即(7)式给出的单量子比特系统从t=0时刻开始随时间演化到t=τ时刻, 进行N次中间测量, 测量时刻. 若N=0 , 表示不进行中间测量. 首先研究约化冯·诺依曼熵S与最后演化时刻τ之间的关系. 如图1 所示, 当不对系统进行中间测量(N=0 ),τ=0 时,S=0,然后S随τ单调递增, 当τ较大时,S值趋近于1. 同时, 图1(a)给出了中间测量次数较小时(N=1,2,4) ,S随τ的变化曲线. 可以看出, 整体上S随τ是逐渐增加的, 同时S伴随着明显的不规则振荡现象, 振幅随τ逐渐减小. 图1(b) 给出的是中间测量次数较大时(N=10,102,103,104),S随τ的变化曲线. 可以看出,S随τ单调递增; 测量次数较大,S来不及完成振荡就被测量破坏掉了, 所以观测不到S随τ的振荡现象.当测量次数N=104时, 由于量子芝诺效应,S随τ的变化曲线几乎与不对系统进行中间测量的曲线重合[20,21]. 在相同τ, 有中间测量时S的值总是大于或等于无中间测量时S的值. 根据(4)式给出的约化冯·诺依曼熵的定义及其意义, 这些结果意味着随τ逐渐变大, 系统由纯态变成混合态, 最后趋近于最大混合态; 在有中间测量时, 系统变成最大混合态更快些. 其次研究约化失衡度D与最后演化时刻τ的关系. 图2 给出的D随τ的变化趋势与图1 中约化冯·诺依曼熵S随τ的变化趋势相反. 详细地, 当N=0 时,D随τ由 1 单调递减, 当τ较大时,D趋近于 0 . 图2(a)表明中间测量次数较小(N=1,2,4) 时, 整体上D随τ逐渐减少, 同时D伴随着明显的不规则振荡现象. 图2(b)表明中间测量次数较大(N=10,102,103,104) 时,D随τ单调递减;同时, 当N=104时,D随τ的变化曲线几乎与不对系统进行中间测量时的曲线重合. 根据(5)式给出的约化失衡度D的定义及其意义, 这些结果也意味着随τ逐渐变大, 系统由纯态变成混合态, 最后趋近于最大混合态; 在有中间测量时, 系统变成最大混合态更快些. 图1 中间测量次数不同时约化冯·诺依曼熵 S 随最后演化时刻 τ 的变化曲线 (a) N=0,1,2,4 ; (b)N =0,10,102,103,104 , 外 界驱动强度 κ=0.95,退相位噪声强度γ =0.2Fig. 1. The reduced von Neumann entropy S varying with last moment τ , where (a) N=0,1,2,4,(b) N=0,10, 1 02,103,104 ,the driving amplitude κ=0.95,the dephasing intensity γ=0.2 . 图2 中间测量次数不同时约化失衡度D 随最后演化时刻 τ的变化曲线 (a) N=0,1,2,4 ; (b) N=0,10,102,103,104 ,外界驱动强度 κ=0.95,退相位噪声强度γ =0.2Fig. 2. The reduced disequilibrium D varying with last moment τ , where (a) N=0,1,2,4,(b) N=0,10,102,103, 1 04 , the driving amplitude κ=0.95,the dephasing intensity γ=0.2 . 图3 中间测量次数不同时量子统计复杂度 C 随最后演化时刻 τ的变化曲线 (a) N=0,1,2,4 ; (b)N =0,10,102,103,104 , 外界驱 动强度 κ=0.95,退相位噪声强度γ =0.2Fig. 3. The quantum statistical complexity C varying with last moment τ , where (a) N=0,1,2,4, (b)N =0,10,102,103,104 , the driving amplitude κ=0.95,the dephasing intensity γ=0.2 . 由(6)式, 结合图1 和图2, 图3 给出了量子统计复杂度C随最后演化时刻τ的变化关系. 图3表明当N=0 时,C随τ由0 单调递增至最大, 然后单调递减至0, 换句话说, 系统复杂性先增加后减小, 在中间某个τ达到最大值. 图3(a)表明中间测量次数较小(N=1,2,4) 时 ,C随τ的变化趋势与N=0 时的变化趋势相似, 但C伴随着明显的不规则振荡现象. 图3(b) 表明中间测量次数较大(N=10,102,103,104) 时, 几乎观测不到C随τ的振荡现象;N越小, 在越小的τ,C又回到 0 值; 当测量次数N=104时,C随τ的变化曲线几乎与不对系统进行中间测量的曲线重合. 总之, 这些结果意味着, 可以通过控制中间测量次数以及系统的演化时间来调节末态的复杂度. 图4 中间测量次数不同时量子统计复杂度 C 随最后演化时刻 τ 及外界驱动强度 κ 的变化 (a) N=0 ; (b) N=4 ;(c) N=1000 , 退相位噪声强度γ =0.2Fig. 4. The quantum statistical complexity C varying with last moment τ and driving amplitude κ , where (a) N=0 ,(b) N=4, (b) N=1000 , and the dephasing intensity γ =0.2. 图3给出的是以外界驱动强度κ=0.95 为例.更一般情形, 图4 给出在不同外界驱动强度κ下,量子统计复杂度C随最后演化时刻τ的变化关系.可以看出, 在N=0 时,C随τ的变化几乎与κ无关;在N̸=0 时,C值与κ有 关; 在相同的N不同的κ时,C随τ的变化趋势大体相同. 因此, 影响系统复杂度的主要因素是中间测量次数N和最后演化时刻τ. 利用Lindblad 方程, 在Born-Markov 近似下, 重点讨论N次中间量子测量后, 在最后演化时刻τ, 受外界驱动的单量子比特末态的量子统计复杂度C. 研究发现: 整体上,τ由0 变大的过程中,C从0 先增加到最大值, 然后减小, 直到再趋近于0. 显然, 开始时量子态由(12)式给出, 其为纯态,对应的C为0; 在环境噪声下, 量子态将演变为混合态, 若时间足够长, 将演变为最大混合态, 对应的C也为0.N较小时,C伴随着明显的不规则振荡现象;N较大时,N越小, 在越小的τ,C又回到0 值;N大到一定程度时,C随τ的变化曲线几乎与不对系统进行中间测量的曲线重合. 由于测量导致的波包塌缩机制, 一般情形下,C随τ的变化存在振荡现象. 然而当N=0 时, 中间过程无测量, 不导致波包塌缩,C随τ无振荡现象; 当测量次数N较大时,C来不及完成振荡就被测量破坏掉了, 所以观测不到C随τ的振荡现象. 当测量次数足够大(N=104) 时, 由于量子芝诺效应,C随τ的变化曲线几乎与不对系统进行中间测量的曲线重合. 量子统计复杂度与系统的有序、无序特征有关, 已经用来研究量子相变[10]. 同时在量子计算中, 量子态的有用性和其复杂度紧密相关[22,23]. 量子测量往往会影响被测量的系统, 同时量子测量也是对量子态进行制备、操控以及进行其他量子信息处理的重要手段. 因此, 可以控制中间测量次数以及系统的演化时间来调节量子系统末态的复杂度. 人们借助于量子见证, 对(7)式给出的受外界驱动的单量子比特进行研究, 发现通过调节外界驱动强度可以较好地操控系统的量子性特征[12−15].与此不同,量子复杂度可以表征系统的复杂性特征,因此该研究从新的角度对该系统量子态的特性和量子过程进行认识.同时,单量子比特是最简单的量子系统,本文结果表明,在噪声影响和外界驱动下,简单的系统也具有复杂的统计特征,因此该模型可作为研究复杂系统的一个典型例子供人们进一步讨论.2.2 量子统计复杂度
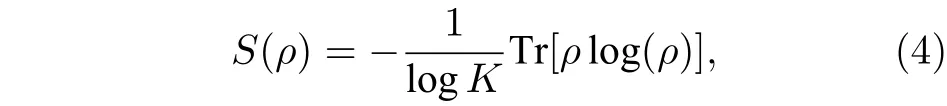
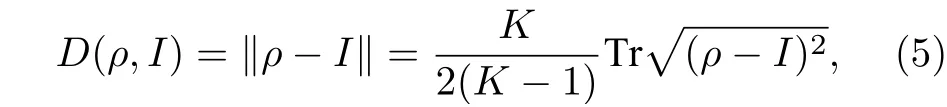
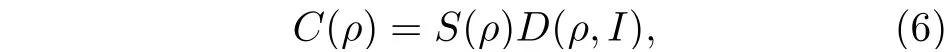
3 模 型
3.1 受驱单量子比特系统
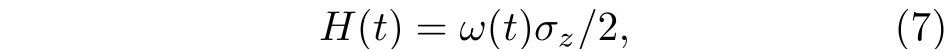
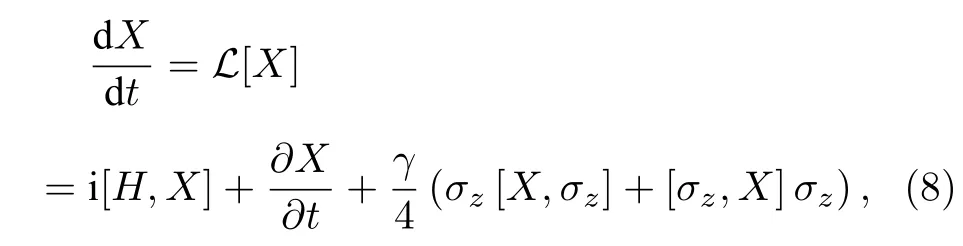
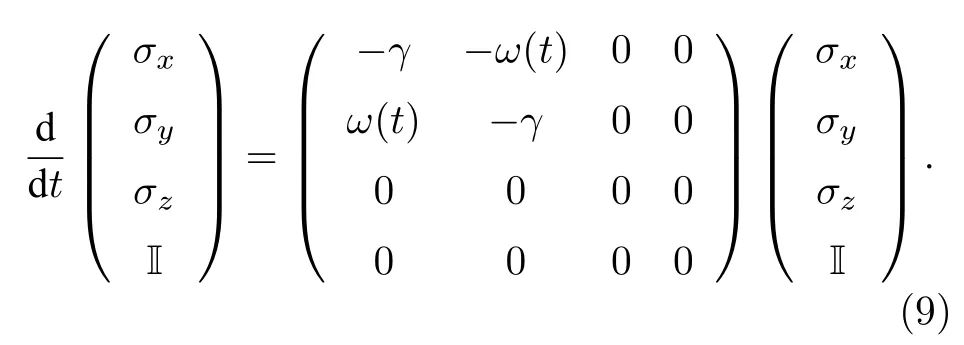
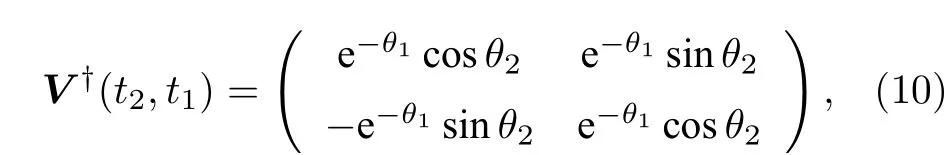
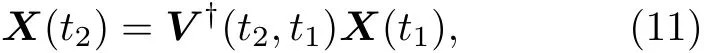
3.2 多次中间量子测量
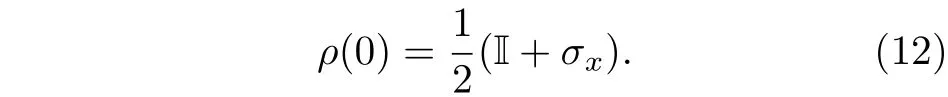
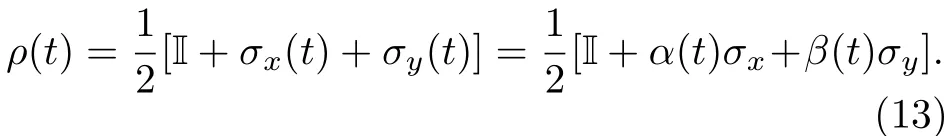
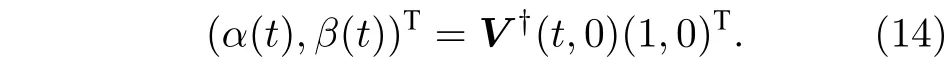
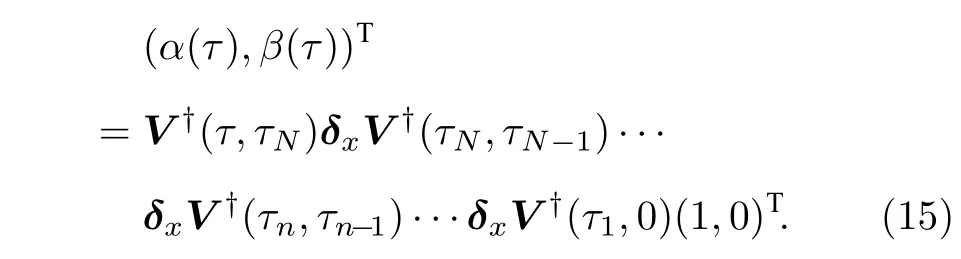
4 数值结果
5 结 论

