旋转二维激子极化激元凝聚涡旋叠加态的动力学特性*
吴昊 任元† 刘通 王元钦 刑朝洋
1) (航天工程大学宇航科学与技术系, 北京 101400)
2) (航天工程大学, 激光推进及其应用国家重点实验室, 北京 101400)
3) (北京航天控制仪器研究所, 北京 100094)
研究了二维激子极化激元凝聚正反涡旋叠加态在半导体微腔极化激元波色爱因斯坦凝聚(Bose–Einstein condensate, BEC)体系旋转情形下的稳定性和动力学特性. 在体系旋转情形下对单分量Gross-Pitaevskii 方程进行重构, 利用四阶龙格库塔方法和时域有限差分方法构建数值模型. 利用实时演化方法研究在体系旋转的情况下, 不同拓扑荷数的正反涡旋叠加态的实时演化过程及稳态局域粒子数和体系旋转角速率之间的关系. 研究了涡旋叠加态激发区域的旋转速率与体系旋转速率的关系, 并阐明了体系的旋转速率对涡旋叠加态相位稳定性的影响机理.研究表明, 半导体微腔极化激元BEC 体系的旋转速率对激子极化激元凝聚叠加态的演化过程及其动力学特性有重要影响.
1 引 言
对于激子极化激元, 尤其是对于微腔激子极化激元的研究, 近来发展十分迅速[1−7]. 微腔激子极化激元是一种光激发, 是部分腔光子和部分量子阱激子的量子态. 半导体平板微腔引入, 实现了实验上对激子极化激元的反交叉色散行为的观测[8,9].观测结果表明, 色散曲线在零波失附近区域有一个明显的下陷, 这表明微腔激子极化激元的有效质量非常轻, 很容易实现玻色-爱因斯坦凝聚(Bose–Einstein condensate, BEC). 而微腔激子极化激元发生凝聚的临界温度可以达到几开尔文, 而且有可能实现更高温度下的凝聚, 尤其是近年来人们发现半导体微腔中的激子极化激元凝聚体系(exciton-polariton condensates)有望在室温下实现BEC[10−13],更给BEC 的应用从实验室走向工程实践提供了可能. 而激子极化激元凝聚体系中自发及可操控的量子化涡旋可用于量子导航、量子计算、量子传输等诸多领域, 具有十分广阔的研究价值[14−21].
其中, 基于激子极化激元BEC 量子化涡旋构建波-粒涡旋陀螺仪在量子导航领域有极大的潜在应用价值. 基于此, 本文提出了实现以BEC 中量子化涡旋叠加态的Sagnac 干涉效应为基础的波-粒涡旋陀螺仪的科学设想[22]. 本质上波-粒涡旋陀螺是一种量子涡旋陀螺, 它利用光与物质相互作用形成的涡旋叠加态作为陀螺效应产生的载体. 而实现这一科学设想的首要前提是对BEC 中涡旋叠加态的陀螺效应加以验证, 因此本文对旋转状态下激子极化激元BEC 中涡旋叠加态的动力学特性进行了研究.
BEC 量子化涡旋的存在形式有单个涡旋, 涡旋阵列和正反涡旋叠加态. 涡旋叠加态是由具有相同拓扑荷数量子数的正反涡旋叠加形成涡旋叠加态. 2012 年Thanvanthri 等[23]研究了基于原子BEC的正反涡旋叠加态在超稳物质波陀螺中的应用, 并首次提出了涡旋干涉陀螺的概念. 2015 年, Padhi等[24]研究了激子极化激元凝聚体系中单涡旋在旋转参考系中形成涡旋阵列中涡旋个数随体系参数的变化规律. 2016 年, Dai 等[19]进一步研究了扁平势和无序势中涡旋叠加态的稳态结构及其Sagnac效应, 理论阐明了涡旋干涉陀螺中Sagnac 干涉相位, 拓扑荷数量子数和半导体微腔BEC 体系旋转角速率三者之间的关系. 在此基础上, 2018 年, 任元等[25]通过数值计算的方法初步验证了在量子涡旋陀螺应用场景下BEC 单支涡旋的动力学特性. 由于波-粒涡旋陀螺是一个崭新的前沿性概念, 因此对于其陀螺效应的实现载体—激子极化激元涡旋叠加态的旋转动力学特性的研究很少, 且人们并未给出涡旋叠加态的演化规律与体系旋转速率间的关系, 也未深入探讨体系旋转角速率、涡旋拓扑荷数与涡旋叠加态的瞬时角速率之间的关系, 而上述问题正是实现波粒涡旋陀螺所必须解决的基础性理论问题.
针对上述问题, 本文利用Runge-Kutta 有限差分方法求解耗散体系的单分量Gross-Pitaevskii(GP)方程, 研究了处于无序势中的二维激子极化激元凝聚正反涡旋叠加态在半导体微腔BEC 体系旋转情形下的稳定性和动力学特性. 通过引入具有时间分量的旋转坐标系, 对GP 方程进行重构, 得到具有科里奥利项的刻画旋转状态的GP 方程. 利用四阶龙格库塔方法(Runge-Kutta method)和时域有限差分方法(finite difference time domain method, FDTD)构建数值模型. 利用实时演化方法研究在半导体微腔BEC 体系旋转的情况下, 不同拓扑荷数的正反涡旋叠加态的实时演化过程及稳态局域激子极化激元粒子数和半导体微腔BEC 体系旋转角速率之间的关系. 研究了涡旋叠加态激发区域的旋转速率与半导体微腔BEC 体系旋转速率的关系, 并给出了半导体微腔BEC 体系的旋转速率对涡旋叠加态相位稳定性的影响. 研究表明, 半导体微腔BEC体系的旋转速率对体系的演化过程和动力学特性有重要影响. 这对于构建极化激元凝聚系统以及后续开发相关陀螺仪设备有重要的理论指导意义.
本文的结构安排如下: 第2 节给出了描述旋转情形下耗散体系的无量纲化形式的GP 方程, 局域激子极化激元粒子数, 涡旋叠加态场分布, 相位分的数值计算方法; 第3 节讨论了正反涡旋叠加态的演化过程与体系会旋转角速率的一系列关系; 第4 节讨论了体系转速在超过107rad/s 量级时体系涡旋叠加态无法保持稳定这一现象在机理层面的探究; 第5 节给出了半导体微腔BEC 体系的旋转速率对极化基元BEC 体系的演化过程和动力学特性的重要影响的相关结论.
2 理论与数值模型建立
单分量模型是直接以下支激子极化激元为研究对象的, 适合于非共振激发, 并探讨激子极化激元的Bose-Einstein 凝聚[26]. 考虑单分量模型:

其中,ψ(r) 是所研究的下支激子极化激元场,P(r)是恒定的外加激励项(泵浦项),g为激子极化激元间的非线性相互作用,V(r) 是物理场所感受到的结构势阱,γ是体系的耗散参数,η是衡量体系饱和的参数, 该方程也称为GP 方程, 是描述Bose物理场的主要手段. 这是由于Bose 体系一般是多粒子体系, 在含有相互作用的情况下, 严格的全量子方法难以求解. 上面所述GP 方程需要有非零的初始物理场条件. 其中, 位置r可以表示为r=本文研究了将整个体系放置在绕体系几何中心匀速旋转的空间中, 涡旋叠加态的演化特性. 为得到可以描述当整个体系处于非惯性空间、围绕激发区域几何中心匀速旋转的情况下, 体系演化的GP方程, 需要对(1)式进行变换. 此时, 将x,y用旋转坐标系表示[27], 即

这样, 将x′,y′代入(1)式, 通过计算, 可以得到体系以Ω为角速率旋转情形下的GP 方程:

对(3)式进行无量纲处理, 可以得到
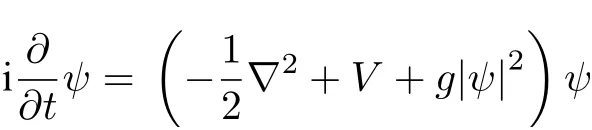

由于使用的数值模型是基于柱坐标系的, 因此使用了如下变换关系:
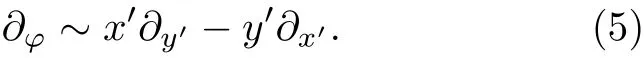
对于柱坐标系下的拉普拉斯算符∇2, 数值模型中将其用差分形式改写, 其中角向与径向分量分别用ρ,φ表示, 具体的差分形式是:


由此可以构建基于四阶龙格库塔方法的GP 方程的差分形式, 即可以对以转速为Ω旋转的体系的涡旋叠加态的场分布、相位分布和局域粒子总数的含时演化特性进行分析.
3 涡旋叠加态在旋转状态下的动力学演化特性
研究激子极化激元凝聚体系中涡旋叠加态的陀螺效应的前提在于分析非惯性系下体系的动力学特性. 简化模型起见, 考虑涡旋叠加态体系围绕其圆心做匀速旋转的情形, 如图1 所示. 此时, 以拓扑荷数为±l的双支涡旋的涡旋叠加态作为GP 方程中激子场分布ψX(r,t) 的初始解. 因此在含时演化的t = 0ћ/meV 时刻(下文中时刻t的单位均为ћ/meV)微腔中存在相干叠加图样(图样呈现花瓣状, 后文简称这种干涉图样为“干涉花瓣”,用以描述激子场的分布)为2l的“涡旋叠加态解”.通过参数的改变, 研究“涡旋叠加态解”随时间演化的动力学特性.
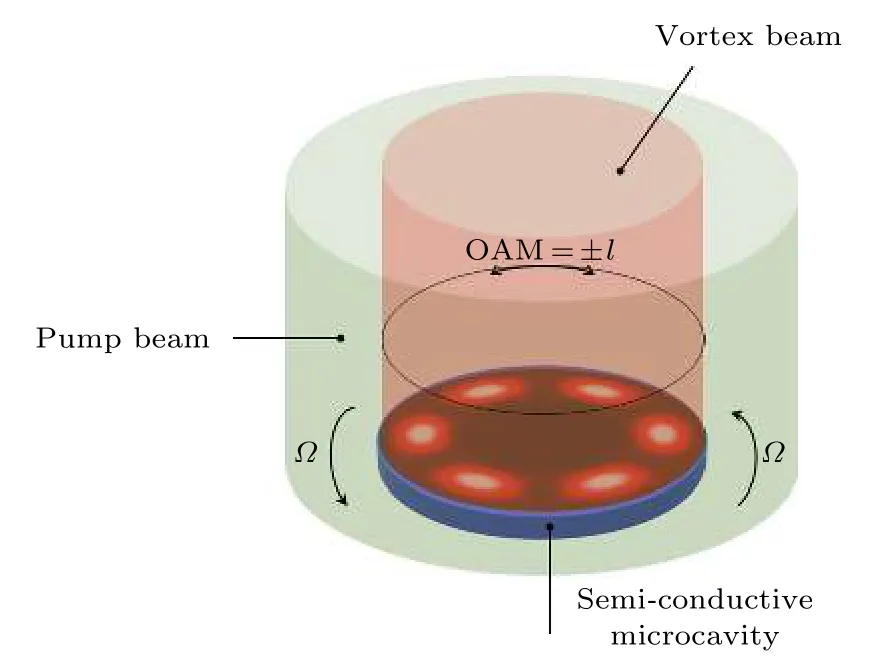
图1 旋转状态下的激子极化激元涡旋叠加态体系Fig. 1. System of exciton polariton condensates on the rotational state.
3.1 体系旋转对涡旋叠加态激子场密度分布的影响
首先考虑拓扑荷数分别为±2 的双支涡旋的叠加情形. 双支涡旋在半导体微腔中发生干涉, 形成关于圆心对称的4 个花瓣状自发辐射场分布极大值区域.现令Ω′=3.81×1010Ωrad/s,其中Ω′为体系的旋转角速率, 而Ω为其无量纲形式, 本文中体系的旋转角速率均由无量纲的Ω给出. 图2(a)为Ω= 0 即体系静止时, 当涡旋叠加态演化至稳态时的激子场分布, 可以发现, 在双涡旋的干涉效应下, 激子场分布在φ= ±45°和φ= ± 135°位置出现4 个极大区域. 如果使激子极化激元体系处于角 速 率Ω约为 4.0×10−7, 8.0×10−7和1.2×10−6的旋转状态下, 则体系的演化状态则会发生很大改变. 从图2(b)—图2(d)的激子场分布可以发现, 体系的旋转影响了涡旋叠加态的干涉效应, 随着旋转角速率的增大, 双涡旋的干涉作用变弱, 而整个势阱内被激发的粒子数却不断增大, 导致干涉相干与相消位置区域连通, 干涉花瓣逐渐模糊.

图2 l=±2 时不同旋转角速率对激发场分布的影响 (a) Ω=0 , t=80ℏ/meV ; (b) Ω=4.0×10−7 , t=80ℏ/meV ; (c) Ω =8.0×10−7 , t=80ℏ/meV ; (d) Ω=1.2×10−6 , t=80ℏ/meVFig. 2. Effects of different angular velocities of the rotation on the exciton field when l=±2 : (a) Ω=0 , t=80ℏ/meV ; (b) Ω =4.0×10−7 , t=80ℏ/meV ; (c) Ω=8.0×10−7 , t=80ℏ/meV ; (d) Ω=1.2×10−6 , t=80ℏ/meV .
旋转速率与激子极化激元涡旋叠加态的演化速率以及稳态时的局域激子极化激元粒子数有密切关联. 双涡旋的拓扑荷数取l=±2 , 旋转角速率分别为(Ω1,···Ωk,···Ω9)=(1.0×10−5,···k×10−5,···9.0×10−5), 可以得到一组激子极化激元体系的含时演化局域激子极化激元粒子数曲线. 首先, 图3(a),(b)反映了Ω1=1.0×10−5和Ω9=9.0×10−5时,局域激子极化激元粒子数处于t=80ℏ/meV 时刻的稳态时, 激子极化激元涡旋叠加态的相位分布. 相位突变处为涡旋产生处, 当转动角速率较小(Ω1=1.0×10−5)时, 相位突变发生于φ= 0°, 90°, 180°和270°处, 而当转动角速率较大(Ω9=9.0×10−5)时, 体系中的涡旋发生分裂, 稳定的涡旋叠加态无法存在, 即双涡旋干涉现象逐渐消失, 激子场联通成一个环状.
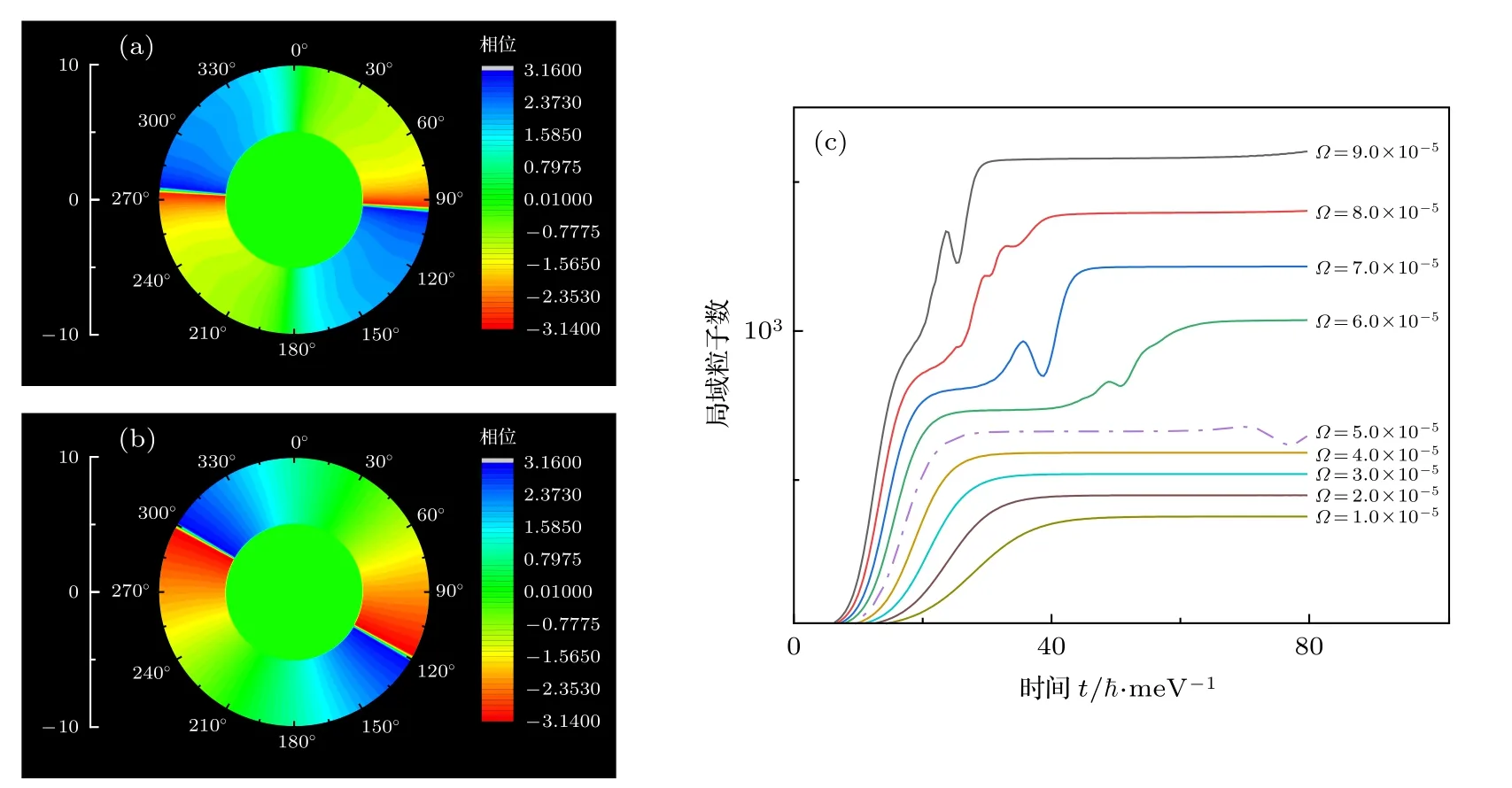
图3 转动角速率与涡旋叠加态演化的关系 (a) 当 Ω 1 =1.0×10−5 , t=80ℏ/meV 时, 激子极化激元涡旋叠加态的相位分布;(b) 当 Ω 9 =9.0×10−5 , t=80ℏ/meV 时, 激子极化激元涡旋叠加态的相位分布; (c) 当体系处于不同转速时激发区域内局域粒子数随时间的变化Fig. 3. The relationship between angular velocities of the rotation and the evolution of superposition state of vortexes: (a) The phase distribution of the superposition state of exciton polariton vortexes when Ω 1 =1.0×10−5 and t=80ℏ/meV ; (b) the phase distribution of superposition state of exciton polariton vortexes when Ω 9 =9.0×10−5 and t=80ℏ/meV ; (c) the description curve of the relationship between time and quasi-particle number on various speeds of rotation of the system.
又如图3(c)所示, 进一步通过对局域激子极化激元粒子数随时间变化的关系可以发现, 当旋转角速率增大, 激子极化基元体系的含时演化速率也会增大, 旋转速率与激子极化激元体系达到稳态所需时间负相关. 而在泵浦光形式、化学势和能量一定的情况下, 体系旋转速率越高, 激子场密度越大,这说明旋转会促进激子极化激元的激发, 使稳态时体系的局域极化激元粒子数大大增加. 转动角速率越大, 涡旋叠加态越容易在更短的时间内达到稳态. 这可能是因为转动破坏了原有的涡旋叠加态结构, 使大涡旋裂化为更小的涡旋, 这一过程促使光-激子场能量耦合增强. 而在其他参数一定的情况下, 体系旋转速率越高, 激子场密度越大, 这说明体系旋转会促进激子极化激元的激发, 使稳态时局域极化激元粒子数增加, 且当旋转角速率小于Ω5=5.0×10−5时, 激子极化激元体系能够在相对久的时间内维持弱平衡状态, 局域激子极化激元粒子数随时间的涨落是非常微幅的. 而当旋转速率超过Ω6=6.0×10−5时, 涡旋叠加态体系局域激子极化激元粒子数会迅速饱和, 此后粒子数会随时间变化发生明显的涨落, 这表明激子极化激元涡旋叠加态体系在较高的旋转速率情形下难以维持长久的平衡状态.
在较小的转动角速率情况下, 局域粒子数不随时间产生明显的涨落, 但涡旋叠加态的干涉位置依旧会随时间发生变化. 以旋转角速率Ω=9.0×10−7、拓扑荷数l=±2 和泵浦光为半径 6 00 µm 的高斯光束为计算条件, 研究处于ρ∈(5,10) µm 的环状无序势阱中涡旋叠加态干涉花瓣位置随时间变化的情况. 如图4, 依次是t为0, 15, 30, 45, 60,75ћ/meV 时刻涡旋叠加态的激子场分布情况. 可以发现如下规律:
1)干涉极大区域在ρ方向的分布不随时间推移而变化, 此处干涉极大区域(花瓣中心位置)在演化过程中始终位于ρ=7.5 µm 处;
2)随时间推移, 二维空间中的激子极化激元向环状无序势阱中心集中, 干涉区域随时间演化局域激子极化激元粒子数不断增加, 而势阱外区域的场密度分布不断下降, 至稳态时降为零;
3)干涉花瓣在一段时间内维持初始位置, 在一定时刻后开始旋转, 且旋转方向在每一时刻都保持一致.
3.2 体系旋转速率与涡旋叠加态旋转速率的关系
由3.1 节所述现象之三(干涉花瓣在一段时间内维持初始位置, 在一定时刻后开始旋转, 且旋转方向在每一时刻都保持一致)可以引申出一组研究:涡旋叠加态干涉花瓣的转动角速率是否与体系转速相关. 为降低计算误差, 使用高阶激发, 取拓扑荷 数l=±6 ,计 算 了Ω=2.0×10−7, 4.0×10−7,8.0×10−7. 记涡旋叠加态干涉花瓣的瞬时角速率为Ωvortex. 图5(a)所描述的为体系角速率Ω=2.0×10−7时,t=0ℏ/meV 时 刻 和t=100ℏ/meV 时 刻 涡旋叠加态干涉花瓣的位置对比, 而图5(b)所描述的为体系角速率Ω=8.0×10−7时,t=0ℏ/meV 时刻和t=100ℏ/meV 时刻涡旋叠加态干涉花瓣的位置对比. 在Ω=8.0×10−7时,t=100ℏ/meV 时刻的干涉花瓣相对于初态旋转了更多的角度, 这一点可以在“花瓣晕影”的空间分布上得到体现.
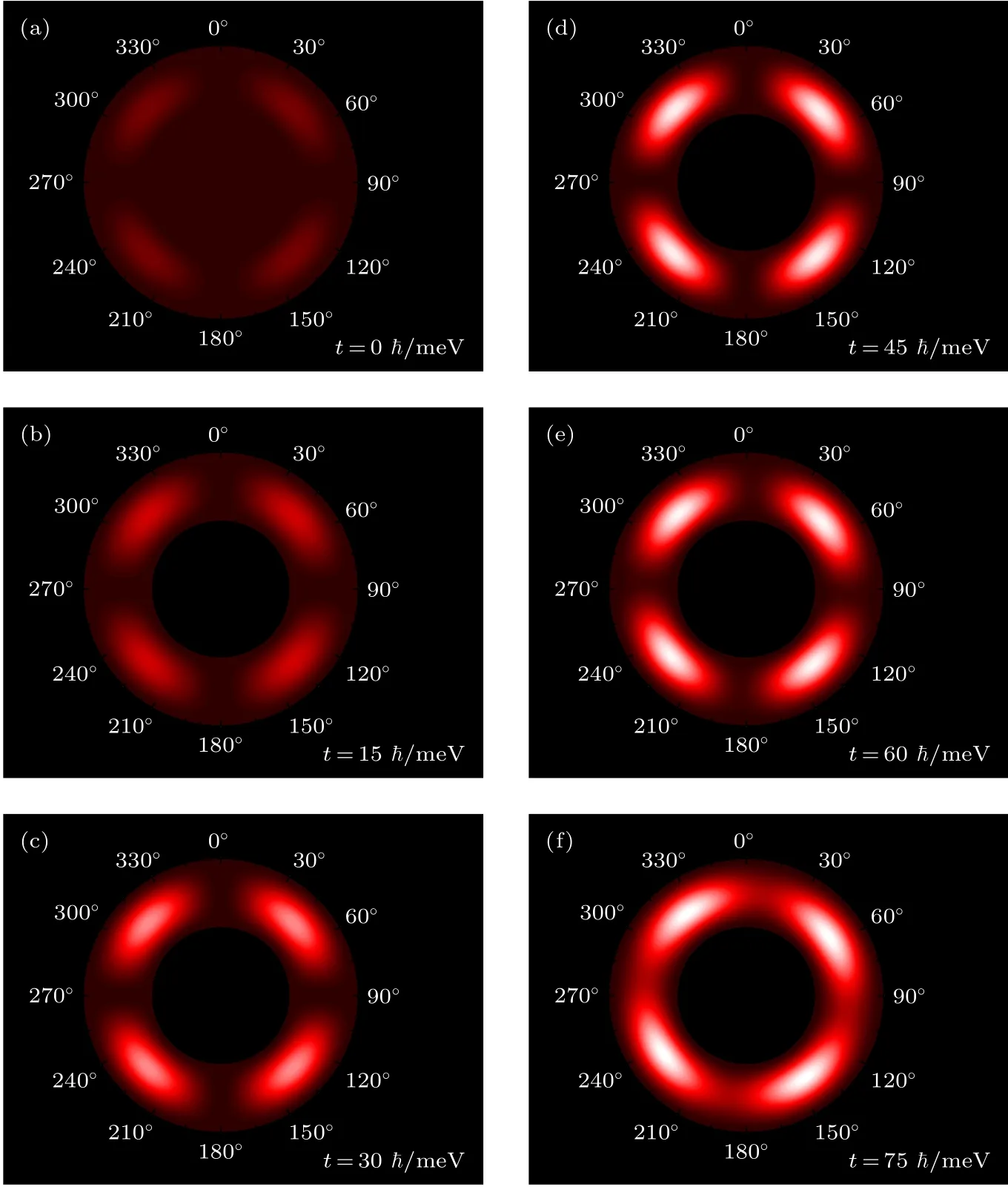
图4 旋转状态下不同时刻的激子场分布 (a) t=0ℏ/meV ; (b) t=15ℏ/meV ; (c) t=30ℏ/meV ; (d) t=45ℏ/meV ; (e) t=60ℏ/meV ; (f) t=75ℏ/meVFig. 4. The exciton field distribution at different moments in the rotational state: (a) t=0ℏ/meV ; (b) t=15ℏ/meV ; (c) t=30ℏ/meV ; (d) t=45ℏ/meV ; (e) t t= 6 0ℏ/meV ; (f) t=75ℏ/meV .
由于当t≥200ℏ/meV 时体系完全失稳而失去研究意义, 因此计算的演化时间限定在200ℏ/meV以内. 图5(c)反映了三种不同旋转角速率下, 涡旋叠加态在演化过程的各时刻的瞬时旋转角速率. 计算表明, 涡旋叠加态从初态到一个中间态的过程中, 干涉花瓣的转动角速率为零. 从该中间态开始,干涉花瓣开始随体系转动而转动, 且Ωvortex的总体趋势是逐渐增大的. 体系旋转角速率Ω越大, 则涡旋叠加态干涉花瓣越早开始旋转, 且Ωvortex的增速越快. 而这一过程也与图4 中的计算结果相吻合.
3.3 体系旋转对不同拓扑荷数涡旋叠加态的影响
最后, 本文研究了体系旋转角速率对不同拓扑荷数的涡旋叠加态的影响. 利用寻找干涉极大区域的中心位置的方法, 可以找出始末时刻“花瓣解”极大值的位置, 从而测算出体系在经历了一段时间的旋转后, 激子极化激元涡旋叠加态旋转的角度. 图6(a)反映了当体系旋转角速率Ω ∈(2.0×10−7,1.0×10−6) 时, 在t=80ℏ/meV 时刻, 拓扑荷数分别为l=±4 和l=±12 的涡旋叠加态相对于初态转过的角度. 如前文所得出的结论, 体系转速越高, 到达稳态时涡旋叠加态相较于初态转过的角度就 越大.当l=±4 时,涡旋叠加态最终转动了14.1°, 而l=±12 时涡旋叠加态最终转动了8.3°.显然, 拓扑荷数越大, 其涡旋叠加态的位置受体系转动影响越小. 图6(b)给出了不同拓扑荷数情况下, 体系旋转角速率对演化过程产生的影响, 其Y轴表示体系到达稳态所需的时间. 可见, 一定体系转速情况下, 涡旋叠加态拓扑荷数与其容易受激发的程度成反比, 因此可以推测, 当拓扑荷数较大时涡旋叠加态更易因体系的旋转而过度激发, 从而失稳. 相反地, 拓扑荷数越小, 涡旋叠加态在旋转状态下的稳定性越好. 这种稳定性来源于相位分布的稳定性, 也即是涡旋的稳定性. 当拓扑荷数足够大时, 涡旋相对更容易被破坏并分裂, 这就表现为体系容易被激发达到饱和状态.

图5 激子极化激元涡旋叠加态瞬时转动角速率与体系转速的关系Fig. 5. The relationship between the instantaneous angular rate of the superposition state of exciton polariton vortexes and the rotate speed of the system.
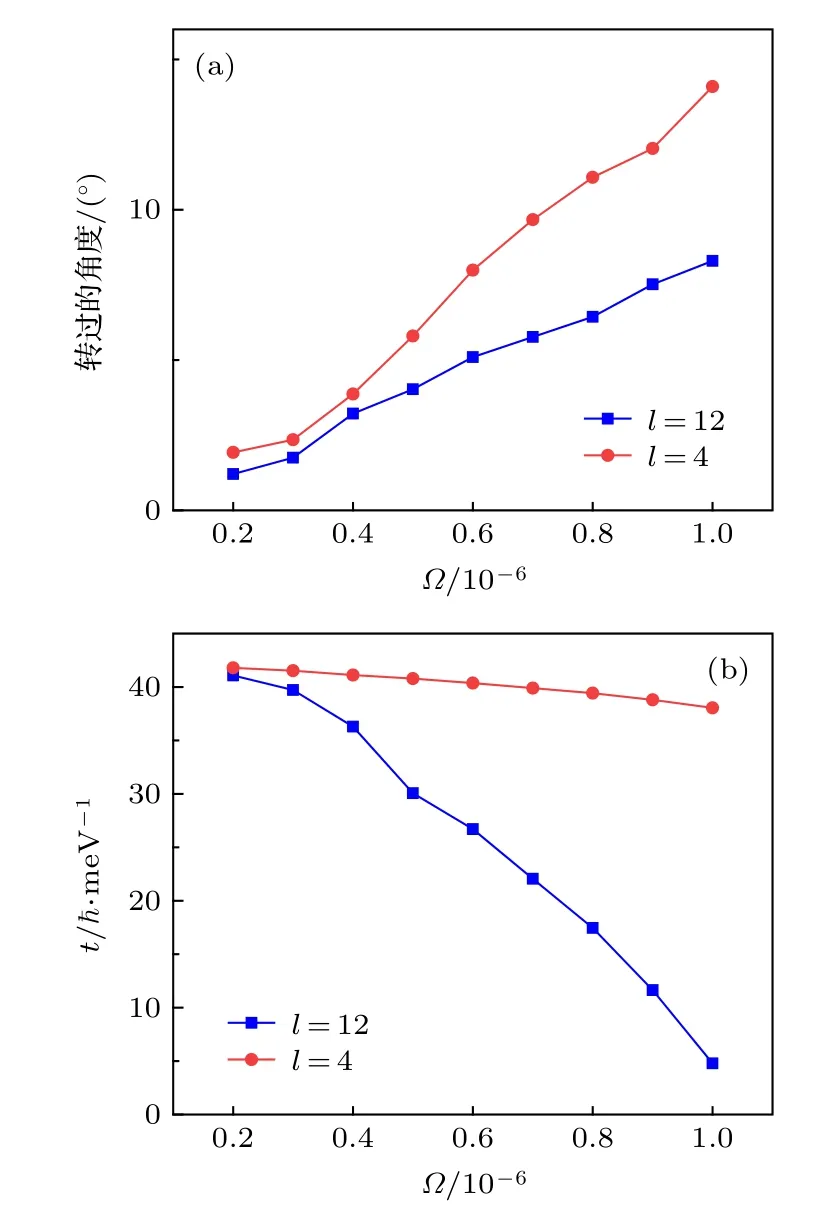
图6 转动角速率对不同拓扑荷数激子极化激元涡旋叠加态的影响 (a)体系旋转角速率Ω ∈(2.0×10−7,1.0×10−6) , t= 80ћ/meV 时 刻, 拓 扑 荷 数分别为l =±4和 l=±12 的涡旋叠加态相对于初态转过的角度; (b)不同拓扑荷数情况下, 体系旋转角速率对演化过程产生的影响Fig. 6. Effects of the angular velocities on the superposition state of exciton polariton vortexes with different topological charge number: (a) Angle of rotation of superposition state vortexes to the initial state at the moment of t= 80ћ/meV with different topological charge of l=±4 and l=±12 in the angular rate range of Ω ∈(2.0×10−7, 1 .0×10−6) ;(b) effect of the system angular rate on the evolution process with different topological charges.
4 讨 论
当Ω小于 1 0−7数量级时, 若泵浦强度、体系耗散γ、环形无序势阱Vext和衡量饱和参数µ选取得当, 则涡旋叠加态会保持长时间的稳态, 即粒子总数的涨落处于微幅区间中, 涡旋叠加态干涉位置不随时间改变.而激子极化激元凝聚的超流特性也从理论上支撑在惯性系中“干涉花瓣”不随体系转动而发生偏转的设想.然而种种计算表明当体系旋转角速率Ω大于10−7数量级时,涡旋叠加态的演化终究会导致激子极化激元干涉图样发生偏转.可能的解释是,弱平衡下的激子极化激元体系经过足够长时间的演化,其初始的涡旋结构会被破坏掉,而涡旋结构的分裂会导致干涉作用渐渐不明显,最后激子场均匀分布于环形无序势阱中,为化学势与泵浦光所束缚.而体系转动加速了涡旋结构裂化衰减的过程,半导体微腔的材料特性,如无序性和一些晶格特性,使得涡旋结构的裂化沿着旋转的切线方向进行,从而导致在有限的计算时间内就发现了干涉图样的旋转.
5 结 论
研究表明,半导体微腔的旋转速率对激子极化激元涡旋叠加态的演化过程及其动力学特性有重要影响.微腔的旋转会加快激子极化激元涡旋叠加态的演化速度,显著提升结构势阱中激子场密度分布.过快的旋转角速率会破坏激子极化激元凝聚体系的激发-耗散平衡,使体系中的局域激子极化激元粒子数发生大幅涨落,进而破坏原有的涡旋结构,导致涡旋叠加态失稳.研究表明,处于旋转状态下的激子极化激元凝聚体系,其涡旋叠加态并非从初始态起就跟随半导体微腔一同旋转,而是在演化至结构势阱中场密度分布趋于饱和后才开始发生旋转,且涡旋叠加态的转动速率会不断增加,而这种增加与体系转速是正相关的.研究表明,不同拓扑荷数的涡旋叠加态,演化特性受体系旋转的影响不同,高拓扑荷数涡旋叠加态的旋转效应明显弱于低拓扑荷数的情形,拓扑荷数越高涡旋叠加态随体系旋转的现象越不明显.然而,相同体系转速情况下高拓扑荷数涡旋叠加态的演化速度明显大于低拓扑荷数的情形,具有高不稳定性.而当体系的转速ω≤103rad/s量级时,激子极化激元涡旋叠加态会在旋转的体系中保持长时间的稳定且几乎不随体系发生转动,这就意味着在绝大多数的量子涡旋陀螺仪的使用场景中,叠加态涡旋都具备陀螺效应.

