扁长型微瓶腔中的回音壁模式选择及Fano 谐振*

王梦宇 孟令俊 杨煜 钟汇凯 吴涛†刘彬 张磊 伏燕军 王克逸‡

1) (南昌航空大学, 无损检测教育部重点实验室, 南昌 330063)

2) (中国科学技术大学精密机械与精密仪器系, 合肥 230026)

微瓶腔在腔动力学、非线性光学、高灵敏度传感和微型激光器等领域具有非常大的应用潜力. 首先, 从亥姆霍兹方程出发, 详细研究了微瓶腔中的模式场分布理论. 利用电弧放电加工方法, 制备了扁长型微瓶腔.其次, 采用光纤锥波导耦合方式有效激发了微瓶腔中的径向模式和轴向模式, 并且通过调节微瓶腔与波导的耦合间隙, 实现了对微瓶腔的欠耦合、临界耦合和过耦合三种耦合状态控制. 实验中, 光谱中回音壁模式得到很好的模式定位和识别, 最大品质因子Q 值达到1.78 × 108. 通过采用接触式耦合来增强调谐的稳定性, 控制不同的耦合位置实现了谐振模式选择性激发, 得到了稳定并且干净的谐振光谱. 最后, 通过选择光纤锥波导直径观察到了Fano 谐振效应. 所展示的结果对增强微腔传感、非线性光学和腔动力学等应用有重要意义.

1 引 言

光学微腔[1]因具有极高的品质因子(Q)和极小的模式体积在光滤波器[2]、高灵敏度传感器[3,4]、非线性光学[5]、腔量子动力学[6]等领域表现出极其重要的价值和应用前景[7]. 近些年, 微球腔(microsphere)[2]、微环腔(microring)[8]和微盘腔(microdisk)[9]等微腔已经被广泛研究, 它们可将光束缚在赤道附近一个窄环带内, 因此, 统称为“赤道型WGM光学微腔”. 赤道型WGM 光学微腔尽管有着很小的模式体积, 但它们的自由频谱范围(FSR)只与赤道面上的半径有关[9,10]. 微瓶腔不同于赤道型微腔, 经光纤锥波导耦合进入腔体的光会呈螺旋状传播, 绕腔轴传播很多圈后会旋转回到之前的入射点[11], 光会在两个转折点之间来回振荡, 形成轴向模式[12]. 微瓶腔在轴向方向上轴向模式广阔, 不仅可以更好地将光耦合进入微腔, 而且谐振光谱更为丰富, 在腔量子动力学、非线性光学应用、光电子器件等领域极具应用前景[13]. 此外, 轴向模式的存在, 使微瓶腔除了拥有角向FSR 外, 还产生了一种新的轴向FSR[12]. 轴向FSR 通常比角向FSR 要小, 将更容易在整个FSR 范围内调谐, 实现全调谐[14], 便于滤波器和激光器中应用.

早在2004 年, Sumetsky[11]首次研究了扁圆型的微瓶腔结构, 理论研究了这种结构在轴向位置上会形成非兼并谐振模式. 2009 年, 南安普敦大学Murugan 等[15]利用光纤锥波导在微瓶腔不同轴向位置耦合, 实现了104—106量级Q值谐振模式的选择性激发, 2010 年, Murugan 等[16]继续采用两个光纤锥波导与微瓶腔耦合, 实现了上行-下载滤波器. 微瓶腔具有很高Q值, 将光限制在腔轴循环振荡数十万次, 腔内光子具有很长的光子寿命.2013 年, Sumetsky[17]利用纳米级变化的微瓶腔实现了几个纳秒的光延迟器件, 这为传统慢光研究提供了一种新的可能性. 2015 年, 中国科大技术大学Dong 等[18]在保证高Q值前提下, 完成了轮廓纳米级变化微瓶腔的封装, 并验证了器件鲁棒性.

微瓶腔在微型激光器、高灵敏度传感和非线性光学相关应用发展也引人注目. 2017 年, 上海理工大学Gu 等[19]通过调整泵浦光干涉模式以及模式强度与干涉条纹在空间上重叠积分, 在微瓶腔上实现了单模激光输出. 2018 年, 福建师范大学Lu 等[20]通过精细选择微瓶腔与纳米光纤间的耦合间隙, 不仅实现了单模激光输出, 而且控制了输出模式阶数及频段. 在高灵敏度传感应用上, 2018 年, 北京航空航天大学Yin 等[21]通过聚焦离子束铣削技术处理微瓶腔, 得到了非常规则、易于识别的谐振光谱,非常适用于传感, 压力灵敏度达到了0.136 pm/µε.2019 年, Stoian 等[22]提出了用微瓶腔检测pH 值,在10—15 s 响应时间内, 分辨率达到了0.06 pH.在非线性效应应用上, 2016 年, Asano 等[23]在低至0.45 mW 的泵浦功率下实现了微瓶腔中的受激布里渊散射效应. 2017 年, 中国科学技术大学Chen等[24]实现了微瓶腔中的受激拉曼激光, 在微瓶腔上添加压力实现了调谐, 调谐范围达到32 GHz.2018 年, Yong 等[25]在满足反常色散的条件下实现了微瓶腔中的四波混频效应.

本文将在理论和实验上对微瓶腔做一个整体的展示, 从回音壁模式分布理论出发, 研究微瓶腔的谐振模式特性. 搭建光纤锥波导耦合系统来测试微瓶腔的谐振光谱特性, 实验上在宽波段和窄波段验证谐振性能. 通过改变耦合间隙、选择微瓶腔的耦合点位置和光纤锥波导的直径, 研究微瓶腔与光纤锥波导的耦合特性, 得到不同特性的谐振光谱.在保持耦合系统稳定性前提下实现微瓶腔的选模功能, 为实现稳定、鲁棒性强的微腔器件打下基础.

2 实验装置

2.1 微瓶腔的制备

制备微瓶腔的方法有两种: 一种是热-挤压法[15];另一种是球腔-挤兑法[26]. 本文在上述两种方法基础上进一步改进, 具体制备过程如图1 所示. 取一根处理后的光纤进行电弧放电处理, 放电时间大概为1 s, 多次放电后, 光纤底端形成微球状. 再取另一根处理后的光纤, 移动其与之前形成的微球在水平位置上一定的重叠区域, 最后对重叠区域多次放电后, 由于光纤的表面压力和两端的挤压后形成微瓶腔. 需要注意的是, 制备微瓶腔过程中形成的微球腔尺寸以及重叠区域的大小对微瓶腔的尺寸具有极重要的作用, 制备出的微瓶腔如图1(d)所示.该制备方法与传统的热-挤压法相比, 不需要电弧放电过程中实时控制电机. 与球腔-挤兑法相比, 制备方式相对更加简单, 并且更加省时, 节约资源,而且可以加工出更为扁长的微瓶腔. 此外, 微瓶腔的外形函数直接影响到它的场分布和谐振模式特性, 可以通过控制电弧放电的次数以及重叠区域的大小来达到控制微瓶腔形状和大小.

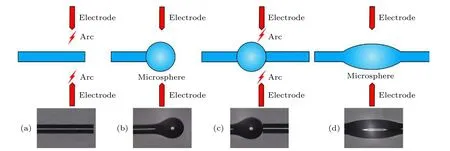
图1 扁长型微瓶腔制备过程图 (a) 对单根光纤放电; (b) 微球腔形成; (c) 第二根光纤对齐; (d) 微瓶腔形成Fig. 1. The fabrication process of prolate microbottle resonator: (a) The single fiber is heated via electrical arc discharge; (b) the microsphere is formed; (c) another fiber is placed to align the microsphere; (d) the microbottle resonator is formed.

2.2 微瓶腔中的回音壁模式

微瓶腔示意图如图2 所示, 主要参数有腔体离瓶颈两端的距离Lb, 腔体两端瓶中心直径Db(半径Rb), 连接微腔的光纤柄的直径Ds(半径Rs), 用近似的抛物线的轮廓模型来拟合微瓶腔的形状[15],轮廓表示为z坐标的函数, 可表示为

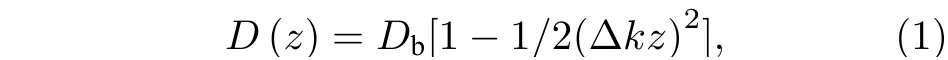
其中, Δk为微瓶腔轮廓曲线的曲率. 利用实验中制备得到的微瓶腔参数对腔体形状进行拟合:Db=150 µm,Ds= 125 µm,Lb= 250 µm, 微瓶腔轮廓拟合结果如图3(a)所示.

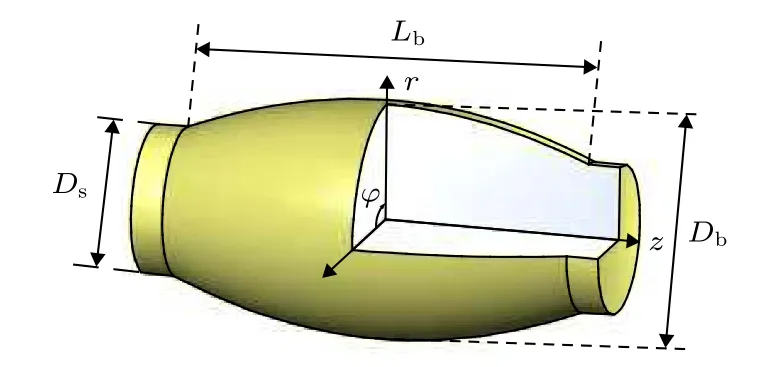
图2 微瓶腔几何形状示意图及其基本参数Fig. 2. Geometrical schematic and basic parameters of the microbottle resonator.

图3 (a)几何轮廓拟合结果; (b)轴向模式(m= 420, p=1, q= 4)场分布图Fig. 3. (a) Fitted result of geometric outline; (b) axial mode field distributions (m= 420, p= 1, q= 4).

微瓶腔的电场满足亥姆霍兹方程:

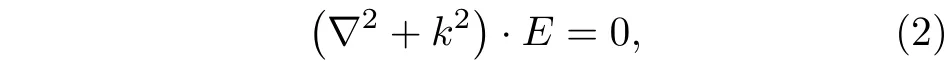
其中,k为传播波矢,∇2为拉普拉斯算符, 可以在柱坐标系下表示为

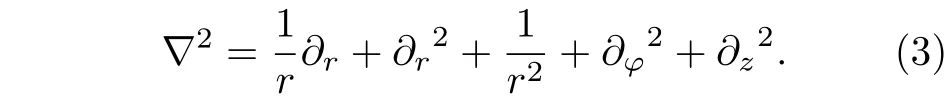
由于微瓶腔在轴向z的半径变化很小, 满足dR/dz≪1, 径向分量的传播波矢kr相对其他两个方向可忽略不计,k表示为

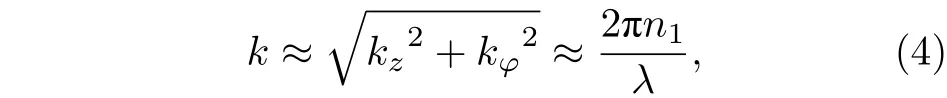
其中,n1为微瓶腔的折射率,λ为真空中传播的波长. 另外, 在对称的微瓶腔中, 在z方向上的投影分量是一个常数值, 有∂zkφ(z)R(z)=0 ; 值得注意的是, 传播波矢的轴向分量在某个特殊位置会消失, 这个位置记为±zc,称为轴向截止点, 有kz(±zc)=0.k在其他两个方向的分量转为

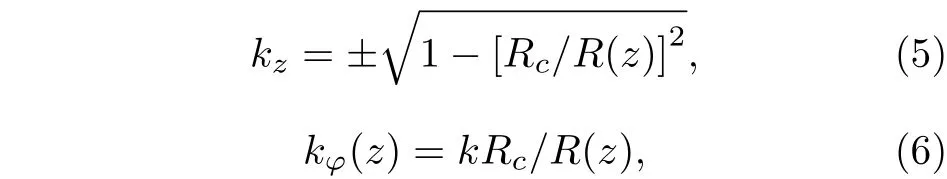
在绝热的条件下近似, 将波动方程分离变量, 根据(2)式, 亥姆霍兹方程可进一步改写为

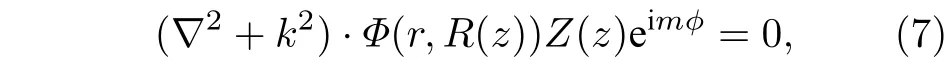
其中,Φ(r,R(z)) 是径向的波函数, 而Z(z)是z向(轴向)的波函数, 根据近似条件∂z2Φi=0 , 波动方程三个分量表示为

其中, 等号左边的项弱相关, 可忽略. 将上面的方程进一步分离为:

用三个量子模式数(m,p,q)来表示微瓶腔的谐振模式,m为微瓶腔的角向模式数,p为径向模式数,q为轴向模式数. 利用径向方向的连续性, 解得径向方向的波函数解:

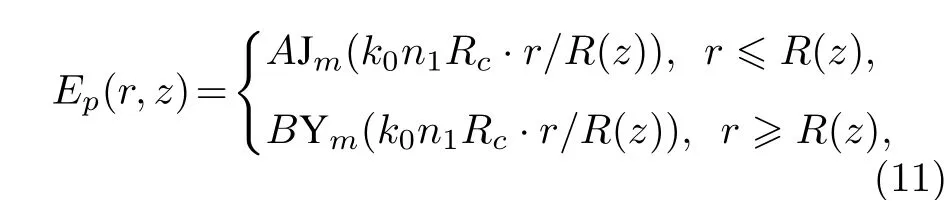
其中, Jm和Ym分别是贝塞尔函数(Bessel function)和修正后的第二类贝塞尔函数,A,B为常数,由电场和磁场的边界连续性条件求得. 另外, 将轴向的波动方程变换为

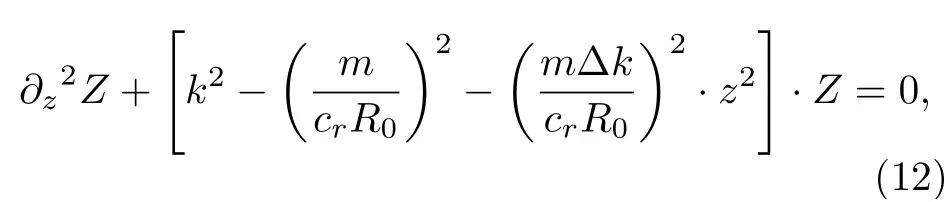
其中,cr是修正因子, 由于在微瓶腔表面的谐振模式, 可令q= 0 求得. 将(12)式看成一个谐振子振荡模型, 有

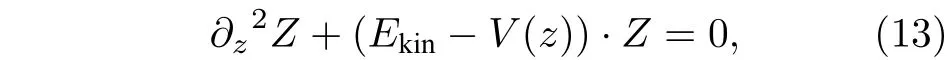
其中V(z)为势能,Ekin为动能. 对比(12)式和(13)式,可得到

可知, ΔEm=2UmpΔk/(crR0) .Ump是Jm(U)函数的解析解, 可表示为Ump ≈m+αp(m/2)1/3+3/20αp2×(m/2)−1/3, 其中,αp是Airy 函数的解析解, 当p=1, 2, 3, 4 时,αp分别等于2.3381, 4.0897, 5.5205,6.7867. 考虑到Z的平方可积性, 传播波矢表示为

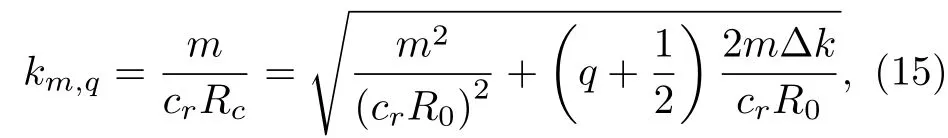
另外, 由在轴向分量上的波动方程(10), 结合kφ(z)=k·Rc/R(z)=m/R(z), 轴向分量上的波动方程表示为

各模式的谐振波长表示为

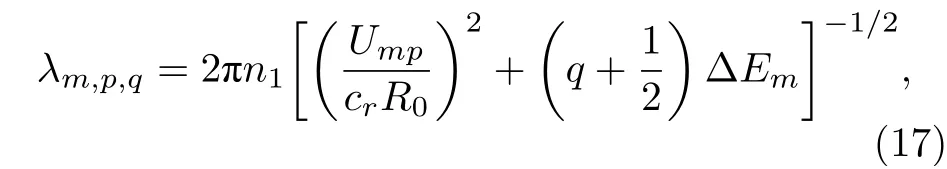
根据方程(17), 由角向模式数m和微瓶腔的尺寸,可解出不同阶的径向谐振波长.

结合上面的分析得到微瓶腔内谐振模式的电场模式分布方程, 表示为

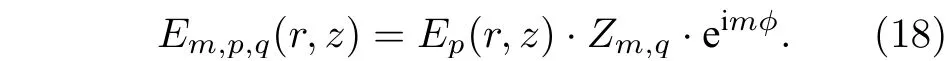
从上面的理论结果得到微瓶腔两种谐振模式,分别为径向模式和轴向模式, 如图4(a)所示. FSR分为角向模式FSR 和轴向模式FSR, 其中, 角向模式FSR 表示为

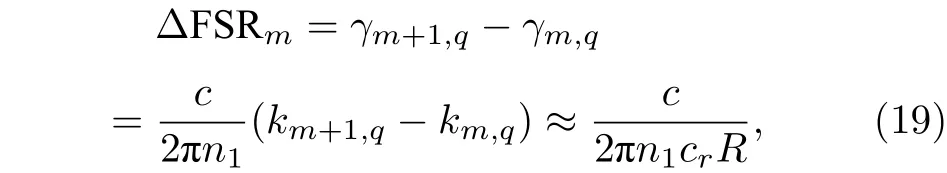
轴向模式FSR 表达式为

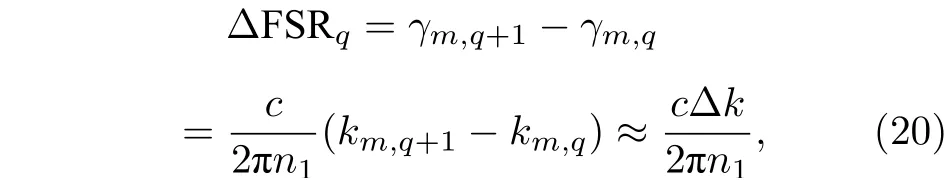
利用如下参数对一阶径向模式下(p= 1)在轴向上的模式分布进行计算: 角向模式数m= 420,Db= 150 µm,Ds= 125 µm,Lb= 250 µm. 图3(b)

给出了微瓶腔在横截面的第五阶轴向模式的归一化强度分布(q= 4), 图4 展示了微瓶腔在z方向上前三阶(q= 0,q= 1,q= 2)模式分布及对应FSR. 可以看出, 在微瓶腔的轴向位置存在明显的轴向模式. 轴向模式受微瓶腔外形轮廓的曲率影响, 可以通过改变轮廓的曲率得到所想要的FSR.另外, 在z方向上, 随着轴向模式数q的增大, 轴向截止点有着更大的移动,Rc的值也减小, 一些高阶模式对应的谐振点也更大.

图4 (a) 相同轴向谐振模式下对应的角向FSR 以及相同角向谐振模式下对应的轴向FSR; (b) z 方向上前三阶(q= 0, q= 1,q= 2)轴向模式场分布图Fig. 4. (a) Angular free spectral range (FSR) with the same axial resonant mode and axial FSR with the same angular FSR; (b) the first three order axial mode field distributions (q= 0, q= 1, q= 2).

3 实验结果与分析

3.1 谐振光谱测试系统

搭建了光纤锥波导耦合系统来测试微瓶腔的谐振光谱特性, 如图5 所示. 实验装置主要包括可调谐激光器、偏振控制器、微瓶腔与光纤锥波导耦合结构、信号发生器和示波器. 可调谐激光器为New Focus Velocity 6728 系列半导体激光器, 线宽小于200 kHz, 波长粗调谐范围为1520—1570 nm,并且可通过电压扫描的方式实现精密调谐, 其中波长的粗调谐由激光器自带控制器实现, 精密调谐需要外接一定频率的周期三角波信号, 由信号发生器提供, 在耦合实验中, 选择频率为20 Hz 的三角波信号来驱动激光器进行精密调谐.

设置1 mW 的泵浦功率避免激发微瓶腔的非线性效应. 使用的光电探测器为InGaAs 材料的高速探测器, 带宽150 MHz, 用来将微瓶腔输出的光信号转换为电信号. 偏振控制器用来调节光纤锥波导中激光的偏振状态, 从而实现微腔谐振模式的高效激发. 可调谐激光器产生的激光首先通过偏振控制器, 之后通过光纤锥波导耦合进入微瓶腔, 光电探测器将光信号转换为电信号后, 在输出端得到透射谱. 另外, 通过精密的三维平移台来调整微瓶腔与光纤锥的相对位置, 在耦合系统的上方和侧方分别布置一个高倍显微观察装置来观测两者的位置,更好地实现高效耦合.

图5 微瓶腔谐振光谱特性探测系统示意图, 插图为微瓶腔与光纤锥波导耦合系统的显微放大图Fig. 5. The detecting system diagram for the resonant spectra characteristic of the microbottle resonators; the illustration is the microscopy enlarged graph of the coupling system consisting of the microbottle resonator and the tapered fiber.

3.2 微瓶腔中的谐振模式与分析

利用锥腰直径为2.4 µm 的锥形光纤波导耦合, 测试了尺寸为Db= 150 µm,Ds= 125 µm,Lb=250 µm 的微瓶腔, 光纤锥波导位于微瓶腔的中心处, 也就是耦合点在中心处时, 激发的谐振光谱如图6 所示, 可以看出, 当逐渐减小耦合间隙, 激发的谐振模式越来越多, 而且, 由于微瓶腔中同时存在径向模式和轴向模式, 光在微瓶腔中走螺旋路线, 方位角模式会出现退简并, 所以微瓶腔的谐振光谱极其密集. 图中标记了一阶径向模式下与理论对应的可能的角向和轴向谐振模式, 所标注的值为相同径向的两个相邻角向模式数和和相邻轴向模式数之间的FSR, FSRm,1–FSRm,6的值分别为3.718, 3.708, 3.716, 3.732, 3.636 和 3.718 nm;FSRq,1–FSRq,6的值分别为1.232, 1.241, 1.239,1.238, 1.237 和1.239 nm. 表1列出了实验测得FSR 值与理论计算得到FSR 值对比结果, 误差均在3%之内. 原则上来说, 在同一个谐振谱中, FSR随着波长的增加会呈现逐渐增大的趋势, 但在本文的结果中, 由于误差的影响存在少许波动, 允许的误差主要来自于瓶腔尺寸拟合中产生的误差、激光器粗扫状态下波长值误差及微瓶腔色散的影响[27].

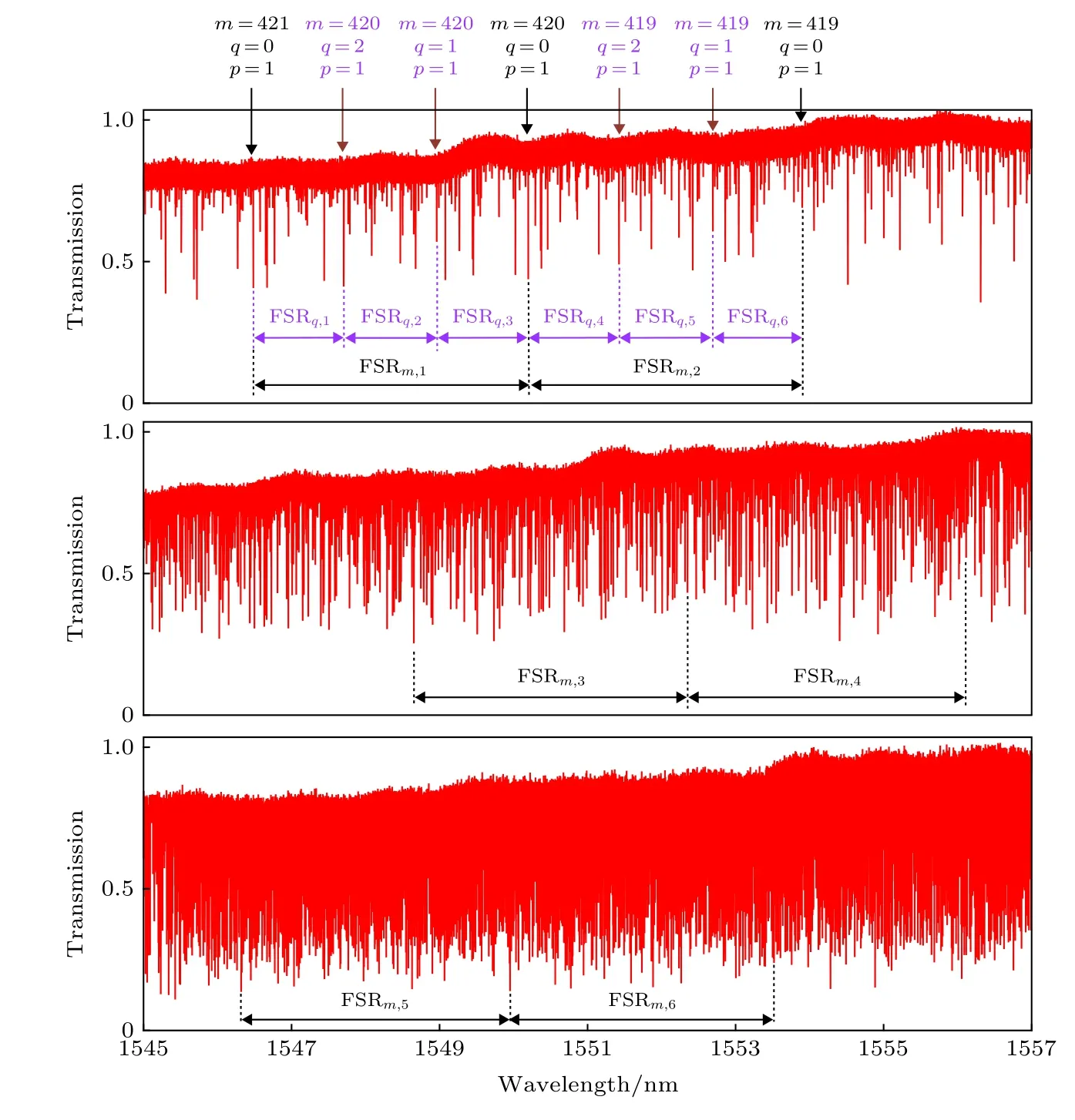
图6 粗扫状态下得到的谐振光谱, 图中标记了一阶径向模式下的角向和轴向谐振模式及对应的角向模式FSR 和轴向模式FSRFig. 6. The resonance spectra of the microbottle resonator for different coupling gaps in coarse scanning, the angular and axial resonant mode in the first order radial mode, angular FSR (FSRq,i) and axial FSR (FSRm,i) are marked in the figure.

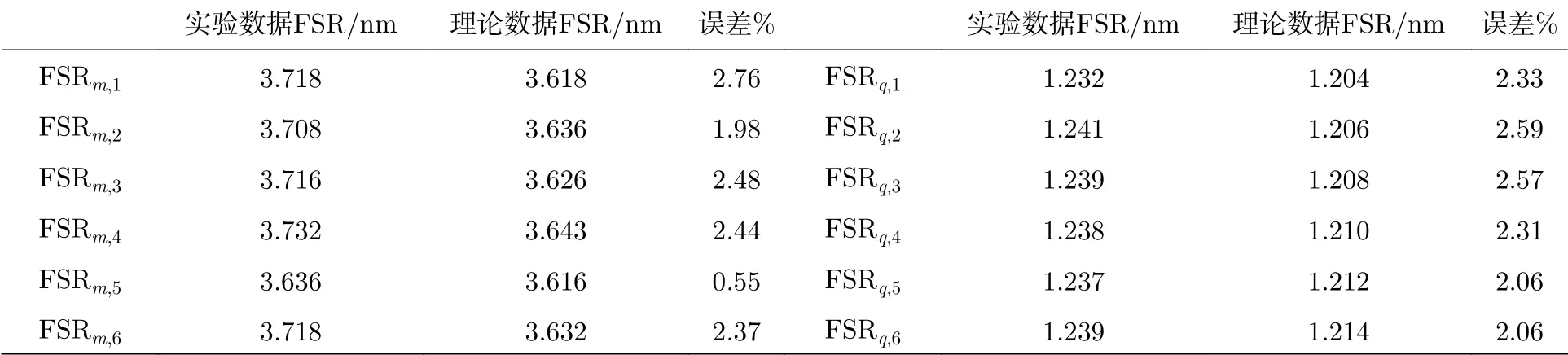
表1 实验测得的FSR 值与理论计算得到的FSR 值比较Table 1. Comparison of FSR value of experimental data and theoretical data.

与角向模式FSR 理论计算公式FSRm,λ=(λ0)2/2πn1crR对照, 代入λ0= 1550 nm,cr= 0.97,R取Rb= 75 µm, 得到理论值FSRm= 3.625 nm,与实验得到的平均值FSRm= (FSRm, 1+ FSRm, 2+…+ FSRm, 6)/6 = 3.705 nm 非常符合. 而轴向模式FSR 理论计算公式FSRq,λ= (λ0)2Δk/2πn1crR,代入λ0= 1550 nm, 轮廓拟合曲率Δk= 0.0046 µm–1,得到理论值FSRq= 1.213 nm, 与实验得到的平均值FSRq= (FSRq,1+ FSRq,2+···+ FSRq,6)/6 =1.238 nm 也非常符合. 很明显, 轴向FSR 要比角向FSR 要小, 相比于同等尺寸的微球腔, FSR 要小很多, 只有它的1/3, 而且微瓶腔两端都有一个柄, 与它连接可以非常方便地通过拉伸或者压缩的方式对微瓶腔中的谐振模式进行调谐, 更容易实现全调谐. 再者, 在一个FSR 内, 存在的谐振模式相比微球腔要多, 主要原因是由于光纤锥波导的锥腰特别细, 除了较容易激发的基模谐振模式外, 还激发了很多的高阶模式, 包括高阶径向模式(p≥ 2)以及高阶轴向模式(q≥ 2).

由于微瓶腔的谐振模式较多, 无法分辨, 调节可调谐激光器为精扫模式, 在很小的范围观察谐振光谱, 图7 给出了通过改变不同耦合间隙位置得到的谐振光谱. 随着耦合间隙g的不断减小, 谐振模式不断激发出来. 在耦合间隙较大的位置, 谐振模式越少. 在g= 1 µm 处, 如图7(b)所示, 基本只有一个模式激发, 而且Q值达到了1.78 × 108. 改变耦合间隙时,Q值也在不断地变化, 实现了对Q值的调控, 而且几乎所有的Q值都在107以上.随着耦合间隙g不断减小, 耦合状态不断变化, 而在耦合状态转变的过程中,Q值呈现减小趋势. 值得注意的是, 尤其在g= 0 µm 时, 也就是光纤锥波导与微瓶腔接触时, 大部分模式也能激发出来,实现良好的耦合. 由于光纤锥波导与微瓶腔处于接触状态, 谐振模式不易受到外界振动的影响, 证明了可以采用接触式耦合的方式来提升微瓶腔的鲁棒性.

图7 精扫状态下不同耦合间隙得到的谐振光谱 (a)实验操作示意图; (b)−(l)逐渐改变耦合间隙测得的谐振光谱图Fig. 7. The resonance spectra for different coupling gaps in fine scanning: (a) Schematic diagram of experimental operation; (b)−(l) the resonance spectra with the gradually changing gap.

当耦合点靠近腔体中心区域时, 即使处于精扫模式下, 激发的谐振模式还是特别多, 因为此处的外形曲线的曲率比较大, 谐振模式包括高阶径向模式和高阶轴向模式都激发了出来. 图8 表示了保证微瓶腔与波导接触的前提下, 选择微瓶腔不同耦合点得到微瓶腔的谐振光谱. 当耦合点位置位于A—D时, 激发的谐振模式还较多, 但当从耦合点移动位置到F后, 谐振模式开始逐渐减小, 尤其当耦合点移动位置到J时, 呈现了一个比较干净的谐振模式光谱. 这是因为微瓶腔中较低阶轴向模式的场分布范围较窄, 而较高阶的轴向模式场分布范围较宽, 耦合点逐渐远离微瓶腔中间位置时, 逐渐越过了较低阶轴向模式的截止点, 因此很多低阶模式不再激发. 但当耦合点移动位置到K时, 没有谐振模式激发, 这是由于加工过程中, 电弧放电作用没有到达微瓶腔的尾端区域, 此外不够光滑, 不能形成回音壁模式. 总的来说, 当光纤锥波导处于不同耦合点时, 得到了不同的透射谱, 在越远离中心区的位置, 激发的谐振模式越少, 因此在微瓶腔中很好地实现了选模, 而且Q值仍非常高.

3.3 Fano 谐振特性

图9 表示了通过改变光纤锥波导直径得到的谐振光谱, 图9(a)—图9(d)分别得到了光纤锥波导直径ρ= 4 µm,ρ= 6 µm,ρ= 8 µm, 和ρ=10 µm 时得到的动态谐振线型. 这些谐振线型从对称的洛伦兹线型开始, 当所选择的光纤锥波导直径增大时, 转变为不对称的Fano 谐振线型. 图中用数字1—6 标记了不对称的Fano 谐振线型. 随着光纤锥波导直径变大, 越来越多的谐振模式转换为了Fano 谐振线型. 尤其是谐振模式4, Fano 谐振线型斜率逐渐增大, 这是由于波导直径变大时, 光纤中的多模与微瓶腔中的谐振模式发生了干涉[28].另外, 不同直径下的光纤传播常数存在差异, 在耦合模理论中可以解释为两个光纤模式与谐振模式相互作用时, 两者存在一个相移[29], 波导中传播常数的变化引起了相移的变化, 从而影响了Fano 谐振线型斜率.

图8 选择微瓶腔不同耦合点得到的谐振光谱 (a)实验操作示意图; (b)−(l)逐渐改变微瓶腔耦合点测得的谐振光谱图Fig. 8. The resonance spectra by choosing different coupling points of the microbottle resonator: (a) Schematic diagram of experimental operation; (b)−(l) the resonance spectra with the gradually changing coupling points of the microbottle.

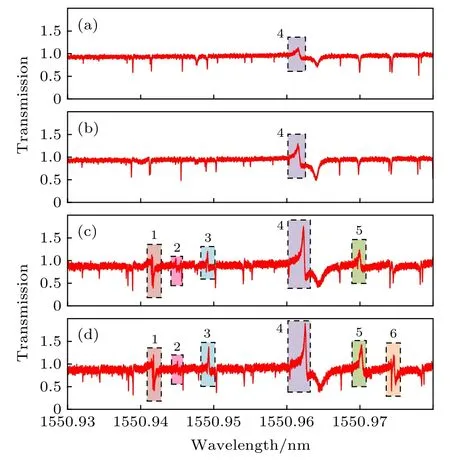
图9 (a)−(d)选择不同光纤锥波导直径得到的谐振光谱, 图中标记了不对称的Fano 谐振线型Fig. 9. (a)−(d) The resonance spectra by choosing different diameters of the tapered fiber waveguide, asymmetric Fanolike lineshapes are marked in the figure.

4 讨 论

从上述实验结果可以看出, 当光纤锥波导耦合微瓶腔中心位置时, 微瓶腔与波导要实现高效耦合, 需考虑两个相位匹配条件, 第一个是微腔与波导两者的传播常数必须要匹配, 第二个是微腔与波导的倏逝场要有足够大的重叠, 第一个条件要求波导必须要足够细, 而本文制备的光纤锥波导锥腰处只有2.4 µm, 保证了微瓶腔中的大多数谐振模式能够被激发, 第二个条件则受微瓶腔与波导的耦合间隙影响, 因此, 从实验的角度, 当耦合间隙较大时, 微腔与波导的倏逝场重叠区域较小, 只有少部分模式被激发, 而当耦合间隙较小时, 微腔与波导倏逝场重叠区域较大, 大部分模式被激发. 从单个谐振模式来看, 耦合间隙较小时, 只有少部分光能进入微腔, 外部波导耦合模式对微腔内回音壁模式场影响较小, 系统Q值接近本征Q值,Q值较大并且Q值受限于本征Q值, 此时Q值最高, 而当逐渐减小耦合间隙时, 进入微腔的光能量越来越多, 波导耦合Q值增大, 总Q值不断减小, 但当耦合间隙过小, 耦合进入微腔的能量又通过倏逝场耦合出了光纤锥波导,所以谐振模式的透过率变小.这中间经历了从欠耦合状态,到临界耦合状态,最后转为过耦合状态.

得益于微瓶腔中狭长的轴向模式,一方面更好地将光耦合进入微腔,便于更好地与光纤锥波导实现稳定耦合,进一步实现稳定的微腔器件,另一方面,也可以通过改变微瓶腔上耦合点位置来实现谐振模式的选择性激发,当从微瓶腔远离中心位置处耦合时,只有较高阶的谐振模式才能被激发,谐振光谱变得较干净,这十分便于在传感领域的应用.此外,还可以通过引入散射损耗的方式,设置截止点来定向选择某些较低模式的光谱[30],得到比较稀疏,容易识别的谱,这些特性也为瓶状微腔在滤波器和传感中的应用带来了极大的便利.

根据上述的结果和分析,本文制备的扁长型微瓶腔所呈现的谐振线型具有以下几个优点:首先,微瓶腔呈现了很高的质量,具有极高的Q值,最大Q值达到了1.78 ×108, 这一结果在窄线宽滤波器、窄线宽激光器、高分辨率传感器以及非线性光学效应等应用领域具有极高的价值;第二,同时激发了微瓶腔的径向模式和轴向模式,具有非常密集的谐振光谱,在腔量子动力学应用中有潜在优势.并且轴向模式FSR 非常小,相比于同等尺寸微球腔的角向模式FSR,只有它的1/3,更容易调谐到指定到频率,实现全调谐,更利于腔动力学、可调谐传感器和可调谐激光器中的应用;第三,在保持微瓶腔与光纤锥波导接触的情况下,在保证可控和强鲁棒耦合的前提下实现了微瓶腔的选模功能,得到了比较干净的谐振谱,调谐过程对外部扰动(如气流和微小机械振动)影响更小;第四,微瓶腔系统中展示的Fano 谐振线型与在片上微腔展示的Fano谐振线型[31]相比,具有更高Q值,进行传感应用上可表现出更高的分辨率;与微球腔耦合系统[32]相比,本文在微瓶腔上展示的Fano 谐振线型具有明显的线型;与多个微腔耦合系统[33]展示的Fano谐振线型相比,本文的系统更加简单,并且实验过程中,考虑了耦合的稳定性和可靠性,可以提升微腔系统在传感、光开关、非线性效应等应用上的性能.

5 结 论

本文详细研究扁长型微瓶腔的选模特性和耦合特性.从波动方程出发研究了微瓶腔中的回音壁模式特性,利用光纤锥波导耦合方式,最大Q值达到了1.78×108,并且展示的轴向模式FSR 非常小,仅为同等尺寸微球腔的角向模式FSR 的1/3.通过选择微瓶腔的耦合点位置,实现谐振模式的选择性激发.通过选择不同光纤锥波导直径,观察到了线型明显的Fano 谐振特性.这些结果将为基于微腔的高灵敏度传感、腔量子动力学以及为增强微腔器件相关应用开辟新的可能性.