基于图形处理器加速数值求解三维含时薛定谔方程*

唐富明 刘凯 杨溢 屠倩 王凤 王哲 廖青

(武汉工程大学, 光学信息与模式识别湖北省重点实验室, 武汉 430205)

量子力学领域中对强激光场与原子分子相互作用的理论研究非常依赖于数值求解含时薛定谔方程. 本文在强场电离的背景下并行求解氢原子的三维含时薛定谔方程. 基于球极坐标系, 采用分裂算符-傅里叶变换方法将含时薛定谔方程进行了离散化. 由此可得到长度规范下的光电子连续态波函数. 图形处理器(GPU)可以依托多线程结构充分发挥细粒度并行的优势, 实现整体算法的并行加速. 计算表明, 相对于中央处理器(CPU), GPU 并行计算有着最高约60 倍的加速比. 由此可见, 基于GPU 加速数值求解三维含时薛定谔方程能够显著缩短计算耗费的时间. 这一工作对利用GPU 快速求解三维含时薛定谔方程有着重要的指导意义.

1 引 言

强场激光物理是过去二十多年随着超短强激光技术的发展而快速发展起来的前沿学科, 主要研究超强超短激光与电子的相互作用. 早在1917 年,爱因斯坦的辐射理论就提出了受激辐射的基本概念, 预测到光可以产生受激辐射. 直至1960 年, 世界上第一台激光器诞生, 此后的几十年间激光技术飞速发展, 从自由输出到调Q技术(Q-switch)、锁模技术(mode locking), 再到啁啾脉冲放大技术,激光的脉冲宽度越来越短, 功率越来越大. 利用先进激光技术获得的超快强激光脉冲与物质相互作用, 成为了研究物质基本性质的一种重要手段. 其中, 强场中一些非线性现象, 如高次谐波的产生(HHG)[1−5]、次序和非次序双电离[6−8]等, 受到了广泛的关注.

强场激光物理的主要理论方法是数值求解含时薛定谔方程(TDSE)[9−11]、强场近似(SFA)[12−14]和半经典模型[15−17]. 求解三维含时薛定谔方程得到的结果可以认为相当于发生在数值上的实验. 但是求解三维含时薛定方程并非一项简单的任务, 无法获得解析解, 只能借助计算机数值求解. 在直角坐标系下哈密顿算符的表示很直观, 但由于正交网格在三个维度上均较为致密, 因此对存储空间和计算量的需求十分巨大. 而在球极坐标系中只有径向网格较为致密, 另外两个维度相对稀疏. 尽管如此,求解三维含时薛定谔方程的计算量也是十分巨大.为了缩短计算的时间, 更快地得到计算结果, 就有必要使用并行方法去加速计算.

在过去的一段时间里, 对基于图形处理器(GPU)并行求解三维含时薛定谔方程的优化与加速主要体现在两个方面. 一方面, 不断改进TDSE算法或者引入其他方法以减小计算量, 如在柱坐标系下采用的混合数值迭代格式[18]. 另一方面, 采用不同的并行平台, 比如: 使用CUDA (compute unified device architecture)平台编写TDSE 程序[19], 使用OpenCL(open computing language)语言编写TDSE 程序[20−22]. 但在CUDA 架构或OpenCL 架构下对算法并行计算进行加速, 使用起来难度较高.

基于硬件的不同, 并行加速有中央处理器(CPU)并行和GPU 并行两种方法. CPU 中多条指令构成指令流水线, 且每个线程都有独立的硬件来操纵整个指令流. 采用复杂的分支预测技术来达到并行计算目的. GPU 是图形处理器, 图形运算的特点是大量同类型数据的密集运算—如图形数据的矩阵运算, 正因为如此, GPU 的微架构就是面向适合于矩阵类型的数值计算而设计的, 这类计算可以分成众多独立的数值计算—大量数值运算的线程, 而且数据之间没有像程序执行的那种逻辑关联性. GPU 并行计算的崛起得益于大数据时代的到来, 而传统的CPU 并行计算已经远远不能满足大数据的需求. CPU 的核处理器相对较少, 并行的效率较低. GPU 最大的特点是拥有超多计算核心, 往往成千上万核. 而每个核心都可以模拟一个CPU 核心的计算功能. 因此GPU 的并行效率比CPU并行效率高.

本文基于GPU 加速数值求解三维含时薛定谔方程, 通过在GPU 上并行加速求解三维含时薛定谔方程, 并且与CPU 并行加速做对比, 得到GPU相对于CPU 的加速比. 在GPU 加速的应用程序中, 工作负载的顺序部分运行在CPU 上(这是为单线程性能优化的), 而应用程序的计算密集型部分并行运行在数千个GPU 内核上. 正是如此, GPU并行计算可以得到很好的加速效果.

2 理论方法

2.1 三维含时薛定谔方程求解方案

物理系统的时间演化由波函数Ψ(t) 来描述, 满足含时薛定谔方程

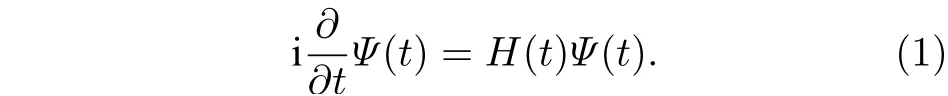
本文以线偏振激光电场作用下的氢原子为例, 在球极坐标中系统的哈密顿量为(如无特殊说明, 下文一律使用原子单位):

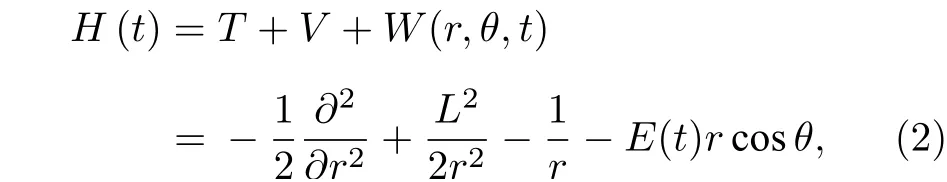
这里H(t) 指作用在约化波函数Φ(t)=rΨ(t) 上的算符, 其中L2为系统的总角动量算符,E(t) 为线偏振入射激光电场.

将波函数Ψ(r,t) 在球谐函数 Ylm(θ,φ) 下展开,

由于m是一个好量子数, 通过对方位角φ进行积分并把角动量算符数值求解.含时薛定谔方程的一般步骤是先给定一个初始波函数Φ(t=0) , 然后将时间演化算符作用在该初始波函数上, 反复迭代直至得到任意时刻的末态波函数. 假设将波函数向前推进 Δt时间增量, 那么t时刻和t+Δt时刻的波函数关系为

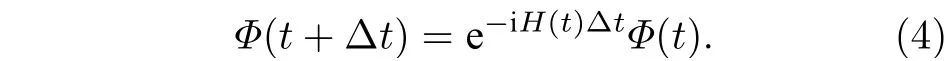
利用分裂算符法[23]将(2)式代入(4)式, 可以得到

这里产生的变换误差为 Δt的三阶误差项. 由于m是一个好量子数, 通过对方位角φ进行积分并把角动量算符Lz替换为它的本征值m, 可以使问题大为简化. 为了方便起见, 下文只讨论m=0 的情况. 假设波函数可以在有限勒让德多项式下展开:

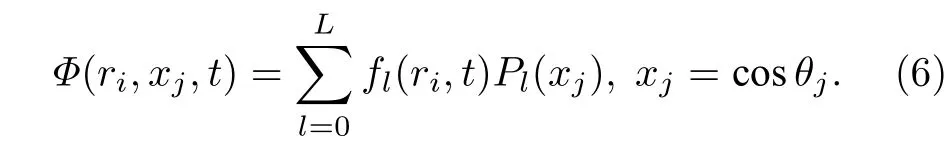
Pl为球谐函数 Yl0,fl(ri,t) 可以由高斯-勒让德求积法数值计算得出,

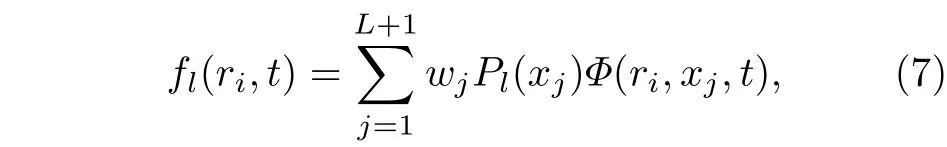
这里xj为勒让德多项式PL+1(xj) 的L+1 个零点,wj为与之对应的求积权重. 对于l的不同取值, 一维径向波函数fl(ri,t) 均定义在R点等距径向网格上, 它的网格表示为

(4)式中时间演化算符的作用可以分为三步.

1) 径向动能算符T=(-1/2)∂2/∂r2独立作用在每个一维径向波函数fl(ri,t) 上, 利用带边界条件的傅里叶谱方法[24], 得到

上述操作中, 由于对所有径向波函数都进行了一维正弦变换, 应用径向动能算符的计算复杂度为O(Rlog2(R)L).

2) 等效势能算符V分为离心势能项L2/(2r2)和库仑势能项-1/r, 其中总角动量算符L2在球谐函数表象下是对角化的, 对角元为它的本征值l(l+1), 因此可以得到

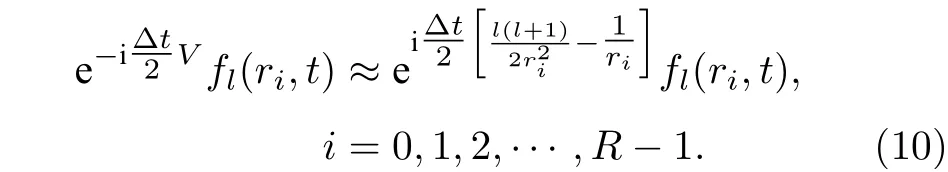
3) 相互作用势能算符W(r,θ,t) 在坐标表象{r,θ}下是对角化的, 利用 (5)式重构波函数Φ(r,x,t) ,得到

上述对应算法步骤如表1 所列.

通过(6)式再次展开成径向波函数fl(ri,t) , 接下来只需要依次执行步骤2)和步骤1), 就完成了波函数向前推进 Δt的一次迭代. 在含时演化中, 重复执行上述步骤, 能够得到任意时刻的末态波函数. 步骤1)中的快速傅里叶变换操作以及(5)式和(6)式中的变换操作都可以通过向量化提高计算效率.

连续态波函数在球谐函数表象下可以写成

其中是σl=argΓ(1+l-iZ/k) 是库仑散射相移,δl是除去长程库仑势的短程势产生的相移.

电子与电场相互作用后的末态动量分布是

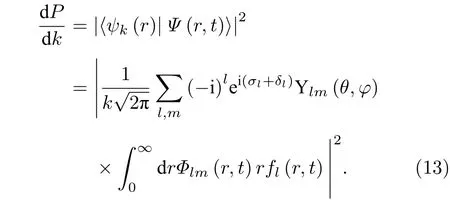
表1 TDSE 算法步骤Table 1. TDSE algorithm steps.

2.2 并行计算方案

本文在Matlab 环境下调用设备端(GPU)来实现并行计算, 离散化的初始波函数以及传播算符均保存在主机端(CPU), 如图1 所示. GPU 上数组的创建和传输通过Matlab 并行计算工具箱的相关函数完成, 使用gpuArray()函数从主机端向设备端发送Matlab 数组, 即将Matlab 工作区内的数组传输到设备端内存. 在GPU 中进行数值计算完毕以后, 再通过gather()函数从设备端向主机端发送Matlab 数组, 即将设备端内的Matlab 数组传输到主机端内存.

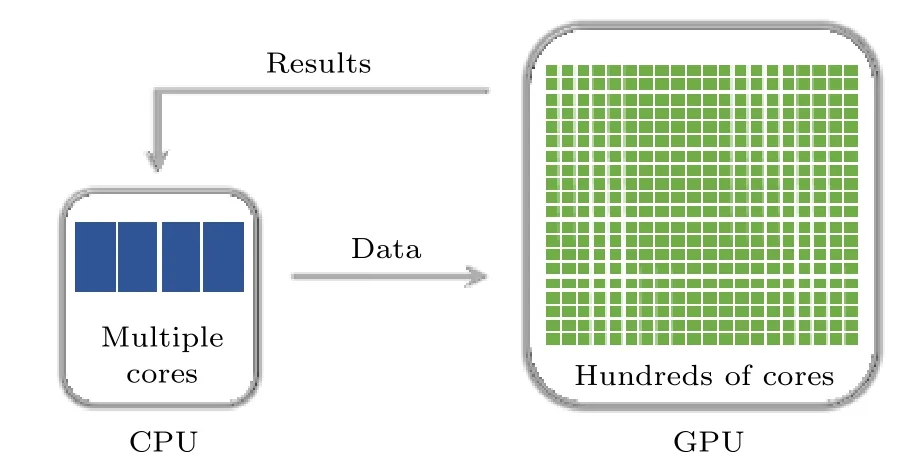
图1 数据传输流程图Fig. 1. The flowchart of data transmission.

在求解含时薛定谔方程时, 具体需要并行计算的部分是: 快速傅里叶变换、逆快速傅里叶变换、矩阵乘法和数组点乘. 将需要进行变换的数组从CPU 传输到GPU, 然后在GPU 上对数组按列分别进行快速傅里叶变换. 不同的列在进行快速傅里叶变换时是相互独立的, 所以可以在不同的线程内对不同的列同时进行快速傅里叶变换, 这样就达到了并行的目的. 计算得到的数组存储在GPU 内存中, 将计算结果传输回CPU 后, 可以释放在GPU中占用的内存. 逆快速傅里叶变换与快速傅立叶变换类似. 矩阵乘法的思路是将左乘矩阵的任一行和右乘矩阵的任一列做点积, 得到目标矩阵的任一元素. 每个目标矩阵元素的计算都是相互独立的, 因此可以同时计算多个目标矩阵元素, 以达到并行计算的目的. 数组点乘是Matlab 中的一种运算方式,直接对两个数组中相同位置的元素做乘法, 即可得到目标数组的对应元素. 因此, 数组点乘本质上是一种标量运算, 非常便于利用多线程进行并行计算.

3 结果与讨论

3.1 测试环境与测试算例

本文所有计算使用的并行环境包含1 个CPU(Intel Xeon E7-8880 v4, 22 核, 主频2.2 GHz)和NVIDIA Tesla P100 卡 中 的1 个GPU (3584 核心, 主频1.3 GHz). 程序的实现基于Matlab 环境,GPU 中的矩阵向量操作调用了重载的Matlab 函数. 本次测试算例以线偏振红外激光电场作用下氢原子的阈上电离为背景. 红外激光电场强度I=9×1013W/cm2, 波长λ=800 nm , 具有正弦平方脉冲包络, 共8 个光学周期. 其中计算采用的空间范围rmax=1000 a.u.,时间步长 Δt=0.0037 a.u..

3.2 实验结果

为获取GPU 并行的优化表现, 需要给出CPU上的并行性能作为基准. 通过改变角量子数L和径向网格点R计算演化时间结束后的末态波函数,比较不同参数下GPU 相对于CPU 的加速比(单个CPU 计算时间与单个GPU 计算时间的比值):

首先, 设置径向网格点R= 1024 × 32 不变,选取不同的角量子数L, 计算结果如表2 和图2 所示.

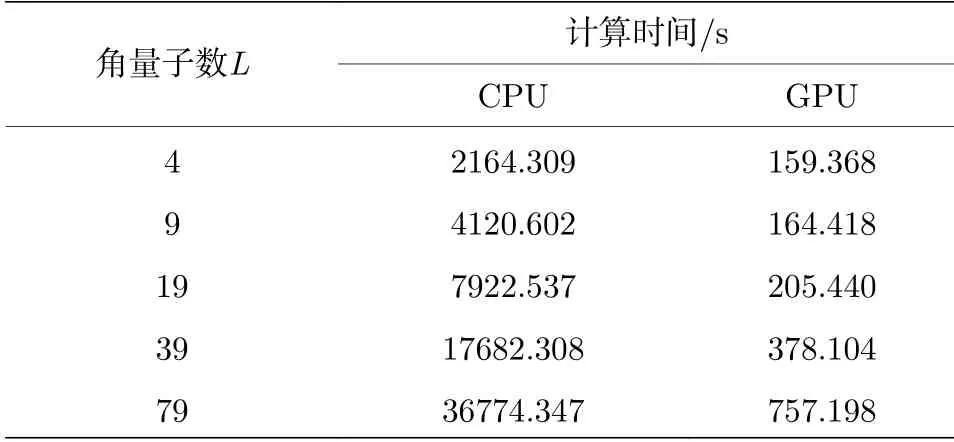
表2 不同角量子数下CPU 与GPU 的计算时间比较Table 2. Computation time of CPU and GPU under different angular quantum numbers.

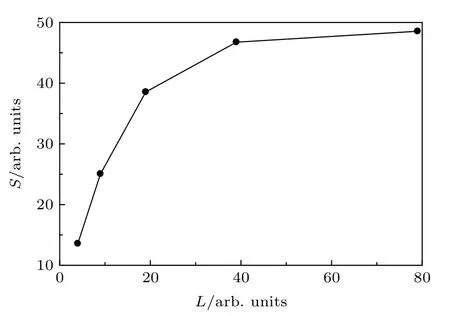
图2 加速比随着角量子数的变化Fig. 2. Speedup ratio as a function of angular quantum number.

角量子数L= 19 保持不变, 改变径向网格点R的大小, 然后将CPU 与GPU 的计算时间对比,如表3 和图3 所示.

同时改变径向网格点和角量子数的大小, 也就是改变径向波函数集{fl(ri,t)}的矩阵大小, 比较CPU 和GPU 的计算时间, 结果如表4 和图4 所示.

此外, 为了进一步测试GPU 的加速性能, 又进行了一组1600 nm 中红外激光的实验, 中红外激光电场强度I=1×1013W/cm2,波长λ=1600 nm ,具有正弦平方脉冲包络, 共8 个光学周期. 其中计算采用的空间范围rmax=1000 a.u., 时间步长Δt=0.0037 a.u.. 此时与第三组实验相同, 同时改变径向网格点和角量子数的大小, 也就是改变径向波函数集{fl(ri,t)}的矩阵大小, 比较CPU 和GPU 的计算时间, 结果如表5 和图5 所示.

选取一组800 nm 激光电场作用下氢原子的阈上电离, 由CPU 计算得到的末态波函数与GPU 的计算结果对比, 如图6 所示, 电子末态动量分布保持一致.

表3 不同径向网格点下CPU 与GPU 的计算时间比较Table 3. Computation time of CPU and GPU under different radial grid points.

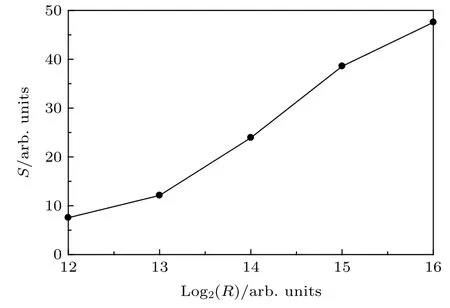
图3 加速比随着径向网格点的变化Fig. 3. Speedup ratio as a function of radial grid point.

表4 不同矩阵大小下CPU 与GPU 的计算时间 比较Table 4. Computation time of CPU and GPU under different matrix sizes.

同时计算两种方法得到的约化波函数的误差为 5×10−21,动量分布误差为 2×10−18. 其中波函数误差计算公式为

动能谱的误差计算公式为

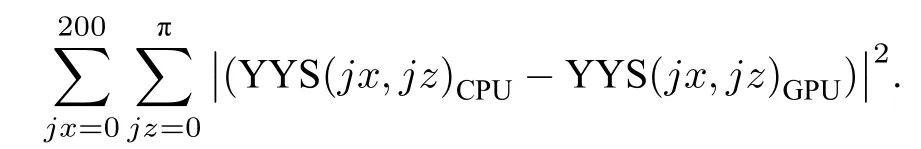
图4 加速比随着矩阵大小的变化Fig. 4. Speedup ratio as a function of the size of matrix.

表5 不同矩阵大小下CPU 与GPU 的计算时间比较 Table 5. Computation time of CPU and GPU under different matrix sizes.

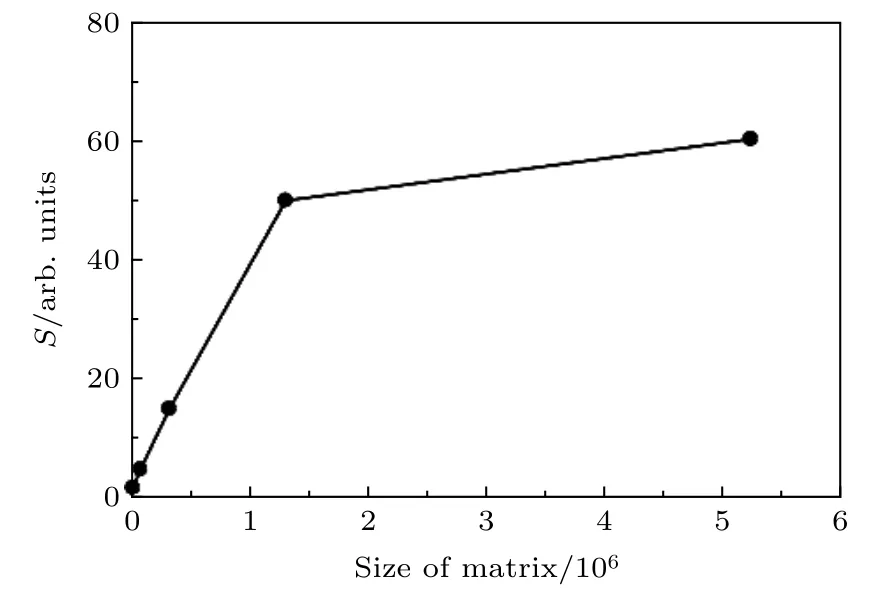
图5 加速比随着矩阵大小的变化Fig. 5. Speedup ratio as a function of the size of matrix.

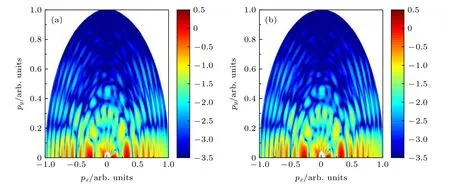
图6 氢原子的光电子末态动量分布(a)CPU计算结果;(b)GPU计算结果Fig.6.Photoelectron final-state mom entum distributions of hyd rogen atom:(a)Calculation results of CPU;(b)calculation results of GPU.

3.3 实验结果讨论

通过上述的计算可以得出:1)相同计算量下CPU与GPU的计算时间有很大的差距,当计算量较小时加速比急剧升高,随着计算量的增大加速比趋于一个稳定值,最高达到了约60倍的加速提升,加速效果十分明显;2)从不同的计算量对比也可以看出,当计算量越大时,加速的效果也就越好.并不是所有的计算都要选取GPU来计算,CPU将数据传输到GPU需要一定的时间,当数据比较大时,采用GPU来并行计算,能够获得更大的加速比;3)如果只是改变一个维度的大小,所得到的实际加速效果有时候并不理想,这和CPU以及GPU存储数据、读取数据的方式有关.所以在计算的时候为了获得最好的加速比,需要同时在至少两个维度上调整矩阵的大小;4)无论采用CPU计算还是GPU计算,都能得到相同的计算结果,计算误差也在可接受的范围内,并且该结果也符合现有的阈上电离物理规律.

4 结 论

本文详细分析了在强场电离的背景下数值求解氢原子三维含时薛定谔方程基于不同硬件的并行速度.借助于分裂算符-傅里叶变换方法,在球极坐标下得到了三维含时薛定谔方程的末态解.同时,依托于GPU的多线程结构,使得GPU发挥细粒度方面的并行优势,实现整体算法的并行加速.采用了CPU并行和GPU并行两种加速计算模式,探讨了两者并行加速的性能.通过与现有的物理规律相对比,验证了程序的正确性.计算结果表明,当计算量较小时GPU相对于CPU的加速效果不突出,随着计算量的增大加速比迅速增加,然后趋于一个稳定值.GPU并行对于数值求解三维含时薛定谔方程有着相对于CPU最高约60倍的加速.可见,计算量越大,采用GPU并行获得的加速比越大.这一工作对利用GPU高效数值求解含时薛定谔方程有着重要的指导意义.