椭球胶体在圆球胶体体系中扩散行为的实验研究*

刘心卓 王华光2)†

1) (苏州大学, 软凝聚态物理及交叉研究中心, 苏州 215006)

2) (苏州大学材料与化学化工学部, 苏州 215123)

复杂受限介质中的扩散行为在自然界是普遍存在的, 与其相关的研究涉及物理学、材料科学和生物学等多学科领域, 受到了这些领域研究者们的广泛关注. 然而, 相比于众多的圆球受限扩散研究, 对形状各向异性的粒子在复杂受限介质中的扩散行为的研究依然比较匮乏. 本文提出了一个简单的软物质实验模型—胶体椭球与圆球混合体系, 来研究形状各向异性的椭球在圆球的受限环境下的扩散行为. 通过描述椭球的运动轨迹和计算粒子的均方位移、范霍夫自关联函数以及非高斯参量, 发现随着圆球浓度的增大, 椭球的平动和转动都被抑制, 出现次扩散行为; 并且, 平动和转动的位移分布也展现出不同的演化行为, 表明这两种运动在高浓度下会发生解耦合. 此外, 在不同圆球浓度下, 椭球都趋向于沿自身长轴方向扩散, 因此在沿长轴和短轴方向的平动受到的受限作用的影响也不同, 导致二者也发生解耦合行为. 综上所述, 受限环境会导致各向异性胶体粒子出现反常扩散行为. 本文的研究有助于理解复杂环境中各向异性物体的扩散和输运行为.

1 引 言

受限扩散和输运是普遍存在的物理现象, 如蛋白质在生物体中的输运[1-3]、示踪粒子在黏弹性液体中的扩散[4-6]以及药物在人体器官中的传递等[7-9].不同体系中的受限扩散输运吸引了物理学、材料科学和生物学界越来越多科学研究者的兴趣, 研究者们试图揭示不同受限扩散的物理机制和行为规律[8,10-13]. 由于空间受限, 阻碍了自由的扩散行为,因此受限扩散会出现反常的动力学行为. 例如, 胶体圆球在自由扩散时, 其运动的均方位移(mean square displacement, MSD)与时间呈线性关系,即 M SD～tβ, 扩散指数β= 1. 而当在玻璃体系中时, 由于受到其周围粒子形成的“牢笼”的限制, 胶体圆球会出现次扩散行为, 此时β< 1[14]. 随着合成制备技术的发展, 各种形状各向异性的胶体粒子被制备出来[15,16]. 研究发现胶体粒子的形状也会对扩散行为产生重要影响[16,17]. 例如, 对于椭球形粒子, 其自由扩散趋向于沿着长轴方向运动, 呈现各向异性的扩散动力学[18]. 更重要的是, 很多的计算机模拟工作表明形状各向异性的胶体粒子在受限情况下, 其扩散会出现更多有趣和奇异的动力学行为[19,20]. 例如在胶体圆球体系中, 随着圆球密度的增大, 体系中菱形或四方形的胶体粒子会发生平动扩散和转动扩散的解耦合(decoupling)行为, 即这两种运动的演化不一致, 平动动力学比转动动力学减缓得更快或更慢, 并且解耦合行为与扩散粒子的形状直接相关[3]. 然而, 相比于众多的计算模拟研究, 形状各向异性粒子的受限扩散的实验研究依然缺乏[21].

本文提出了一个简单的实验模型体系来研究形状各向异性粒子的受限扩散. 将胶体椭球粒子与胶体圆球粒子混合, 研究单个椭球粒子在圆球体系中的扩散行为. 研究发现, 随着圆球浓度的增大,椭球粒子的平动和转动都会减弱, 呈现次扩散行为, 而且在高浓度时转动减缓得更为严重, 说明平动和转动的解耦合行为. 此外, 椭球在不同的圆球浓度下都趋向于沿着自身长轴方向进行平动扩散,说明粒子的平动扩散是由沿着长轴方向的运动主导. 并且, 沿着长轴方向的平动位移会随着圆球浓度增大出现非高斯分布行为, 而沿着短轴方向的平动位移则没有变化, 一直接近高斯分布, 说明这两种平动也发生了解耦合行为. 另外, 转动位移在中间浓度下出现非高斯行为, 而在更高浓度下非高斯行为又会减弱. 这些结果揭示了圆球受限对椭球扩散行为的重要影响, 有助于更好地认识非球形胶体粒子受限扩散的行为规律.

2 实验过程与方法

本实验将少量的椭球与圆球混合, 研究椭球在二维受限体系下的扩散行为. 实验中使用的圆球是尺寸为1.6 µm 的聚苯乙烯微球, 所用椭球是通过物理拉伸方法制得[3], 长轴约为7.0 µm, 短轴约为1.6 µm. 实验时使用移液枪吸取适量混合液, 置于两盖玻片之间, 从而形成单层胶体粒子样品, 如图1所示. 然后利用紫外光胶(norland)对其进行密封.将密封好的样品静置10 h 后, 在显微镜载物台上静置平衡1 h 后进行观察和数据采集, 采集速度为1 帧/s. 为了防止可能出现的样品槽边界效应,选择远离边界的区域来进行数据采集, 并且使视野中只有一个椭球粒子, 避免了椭球粒子之间的相互作用. 图像数据使用通用的粒子追踪程序识别和分析. 本文研究了椭球在不同圆球面积分数(φ)下的扩散行为, 其中圆球的面积分数的计算公式为φ=nsπ(σs/2)2/A, 其中ns是圆球的粒子数,σs是圆球粒子的直径,A表示整个视野的面积.

图1 (a)样品在显微镜物镜上的示意图; (b) φ = 0.57 的样品的显微镜照片Fig. 1. (a) Schematic of the experimental sample on a microscope objective; (b) a bright-field microscope image of the colloidal suspension for φ = 0.57.

3 实验结果与讨论

为了直观展示椭球粒子扩散行为的运动特征,绘制了椭球粒子在不同圆球面积分数下运动100 s的轨迹, 如图2 所示. 在φ= 0.57 时, 椭球粒子的质心可以在很大的空间内移动, 平动运动明显, 表现出无规随机扩散; 粒子取向角度变化频繁, 其转动也呈现无规扩散行为. 然而在面积分数较大时(φ= 0.81), 粒子运动的空间范围减小, 并且粒子的取向几乎不变, 这表明粒子的扩散在平动自由度和转动自由度都受到了抑制.

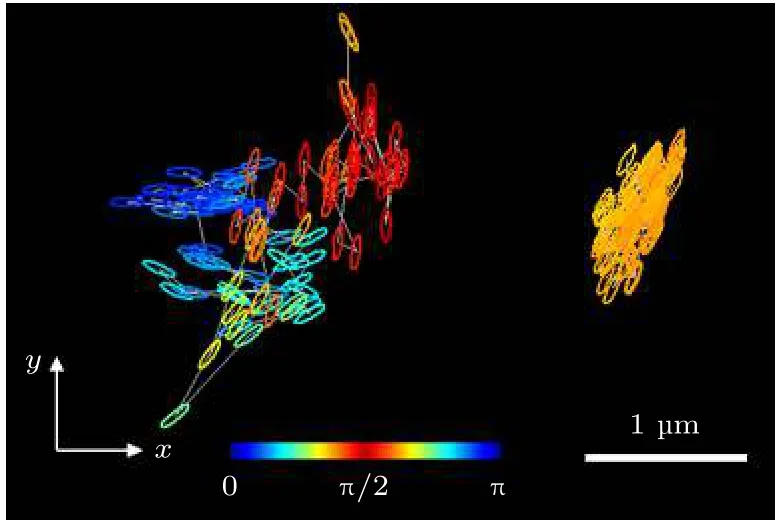
图2 椭球在不同圆球浓度下运动100 s 的轨迹: φ =0.57(左)和φ = 0.81(右). 椭球的不同时刻位置用空心椭圆表示, 其取向是椭球长轴方向和x 轴方向的夹角, 用颜色表示Fig. 2. 100 s trajectories of an ellipsoid at φ = 0.57 (left panel) and φ = 0.81 (right panel). The positions of the particle at different times are indicated by ellipses. The color indicates the orientation of the particle with respect to the x axis.

为了定量地分析椭球的动力学, 计算了不同圆球面积分数φ下椭球的均方位移(mean square displacement, MSD). 得出椭球平动的MSD 为, 转动的MSD 为, 其中r(t) 和θ(t) 分别表示t时刻椭球的中心位置和取向. 图3 展示了椭球在不同圆球面积分数下均方位移. 随着圆球面积分数φ的增大, 平动和转动均方位移均减小, 这源于椭球粒子的运动空间受到了周围圆球粒子的限制, 使其动力学减慢. 并且, 在高圆球面积分数下, 椭球的平动和转动均方位移都呈现出明显的次扩散行为. 为了更好反映这种次扩散行为的演化, 对平动和转动均方位移在1—20 s 的时间范围内进行冥律(powerlaw)拟合: MSD～tβ, 得到了扩散指数β. 图4 给出不同圆球面积分数φ下平动和转动的扩散指数β. 当φ= 0.57 时,β值接近1, 表明圆球粒子的受限影响较小, 椭球表现出普通的扩散行为, 这与轨迹的结果相一致. 随着φ增大, 平动和转动的扩散指数都开始减小, 说明椭球因为周围圆球的受限呈现次扩散行为. 此外, 在较高的圆球面积分数下(φ> 0.75), 转动的扩散指数比平动的扩散系数下降得更多, 表明椭球的转动比平动受限严重. 说明椭球的转动扩散和平动扩散在比较强的受限情况下发生了解耦合(decoupling)行为, 这一结果与四面体、菱形等非球形粒子在浓密的胶体体系中的扩散行为一致[16,19], 表明非球形粒子在受限情况下的转动和平动扩散的解耦合行为具有一定的普遍性.

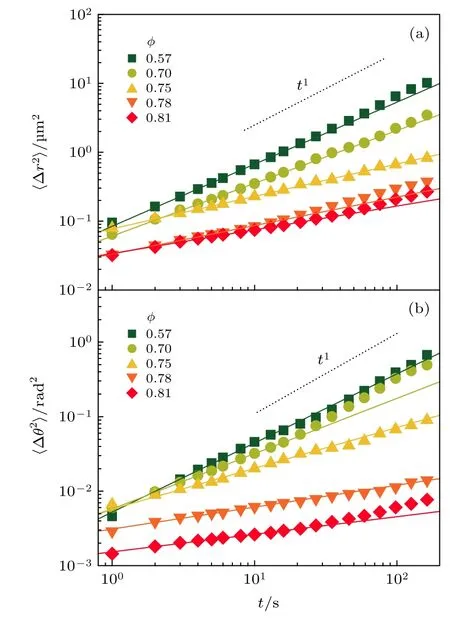
图3 椭球在不同φ 下的平动均方位移(a)和转动均方位移(b), 实线是时间范围为1-20 s 的幂律拟合, ～tβFig. 3. Translational mean square displacements (a) and rotational mean square displacements (b) of ellipsoids at different φ. Solid lines are the power-law fits: ～tβ in the time range of 1-20 s.

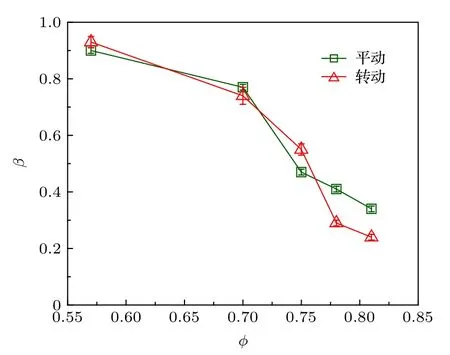
图4 平动和转动扩散指数β 随浓度的变化Fig. 4. The φ dependent β for translational and rotational motions.

为了深入分析椭球粒子的扩散动力学, 本文还计算了范霍夫自关联函数(self-part of the van Hove correlation function), 用来表征椭球粒子运动位移的概率分布. 对于平动, 范霍夫自关联函数为Gs(r,t)=〈δ(r-Δr(t))〉; 对于转动,Gs(θ,t)=〈δ(θ-Δθ(t))〉,其中Δr(t)和Δθ(t)分别是椭球粒子经过t时间运动的平动位移和转动位移. 对平动进行更细致的分析, 将平动位移分解为两部分, 即沿着椭球长轴方向的位移和沿着短轴方向的位移. 图5(a),(b)分别给出了椭球粒子在4 s 内沿着长轴方向和短轴方向的平动位移的概率分布. 结果表明, 在任意圆球面积分数φ下, 沿椭球长轴方向的平动位移分布始终比沿短轴方向的平动位移分布要宽, 说明椭球粒子更倾向于沿其长轴方向进行扩散. 这与在没有受限情况下的椭球自由扩散行为一致[11], 表明这种各向异性的扩散行为与周围圆球的受限环境无关.然而, 随着圆球面积分数φ的增大, 沿椭球长轴方向的平动位移分布逐渐偏离高斯分布, 在高面积分数呈现非高斯行为; 而沿椭球短轴方向的平动位移始终接近高斯分布. 这说明随着φ的增大, 沿椭球长轴方向和短轴方向的平动行为也发生了解耦合,并非发生同样的演化行为. 图5(c)展示了对应的转动在不同圆球面积分数下的位移分布, 与前面两种平动位移分布的演化都不相同. 转动位移分布只在中间面积分数先呈现显著的非高斯行为. 这进一步说明了随着φ的增大, 椭球粒子的平动和转动扩散演化不同步, 两种运动发生解耦合.

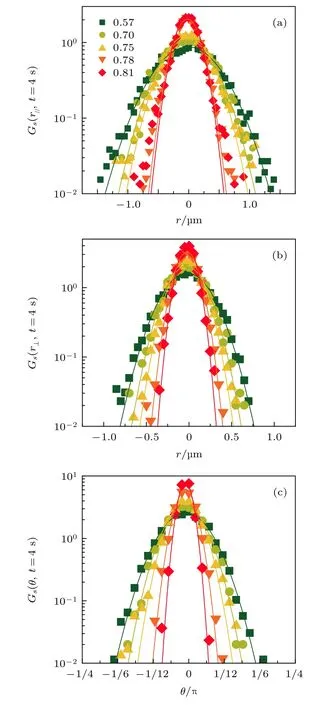
图5 椭球在不同φ 运动4 s 的位移分布 (a)沿长轴方向平动位移; (b)沿短轴方向平动位移; (c)转动位移. 实线是高斯拟合Fig. 5. The distribution of the ellipsoid displacement for lag time of 4 s at different φ: (a) Translational displacement along the long axis of the ellipsoid; (b) translational displacement along the short axis, (c) rotational displacement.Solid lines are the best Gaussian fits.

为了进一步确认位移分布的非高斯行为, 计算了非高斯参量:a2= 1/2〈Δ4(t)〉/〈Δ2(t)〉2-1 , 其中Δ(t)代表椭球粒子经过t时间运动的平动位移或转动位移. 图6 给出了椭球粒子运动t= 4 s 的平动位移非高斯参量和转动位移非高斯参量. 对于沿椭球长轴方向的平动位移,a2随着圆球面积分数φ的增大而变大, 证实了其位移分布越来越偏离高斯行为. 这与胶体玻璃化转变中的结果相似, 即在体系浓度越来越高时, 粒子运动受到的牢笼效应越来越明显, 并出现逐渐增强的次扩散行为和非高斯行为[22]. 这里, 随着圆球面积分数增大, 椭球运动受到由圆球构成的牢笼限制, 从而导致了非高斯行为. 然而, 对于沿椭球短轴方向的平动位移,a2保持很小的值, 表明其接近高斯行为, 与位移分布的结果相一致. 可能的原因是椭球平动趋向于沿长轴方向扩散, 而沿短轴方向的扩散本身就很小,因此牢笼效应主要影响沿长轴方向的运动, 引起非高斯行为; 而对短轴方向的扩散影响较小, 依然保持高斯行为. 对于转动位移,a2先增大后减小, 呈现非单调变化, 与转动位移分布结果一致. 这种增大是源于圆球的牢笼效应, 而减小则可能由于在很大的圆球面积分数下, 相比于平动, 椭球的转动已经被强烈限制[22], 均方位移的结果也说明了这一点. 因而导致了a2减小, 使转动位移趋向高斯位移分布. 这与圆球胶体体系发生玻璃化转变后的非高斯行为相似, 这种情况下粒子平动运动被冻结后,非高斯行为会减弱[11]. 在本文的体系中, 由于椭球在高面积分数下, 其转动相比于平动先被冻结[22],因而转动的非高斯行为会在高面积分数下减弱, 对应的位移分布又趋向高斯行为.

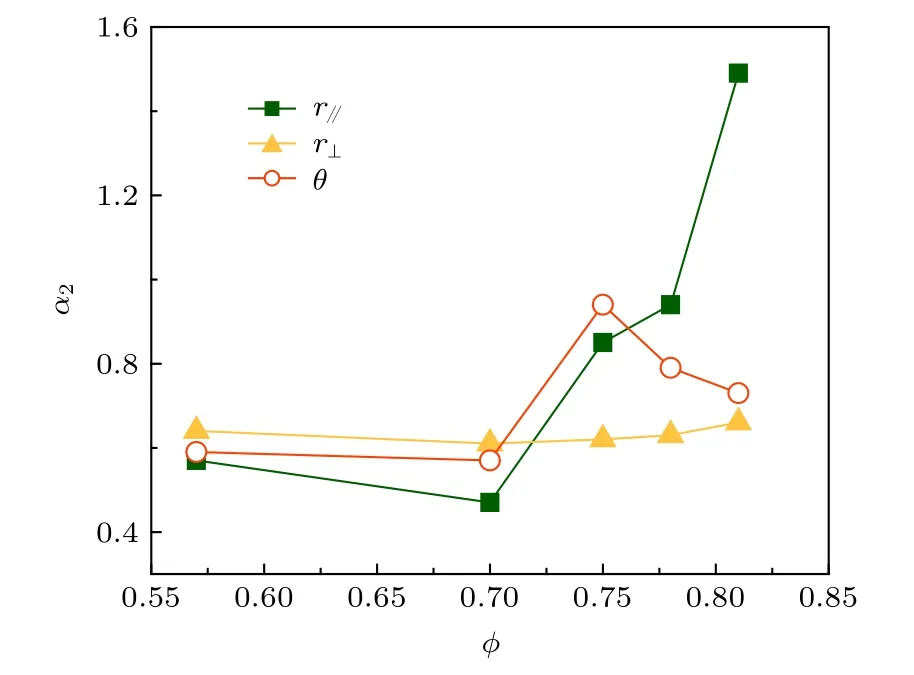
图6 椭球运动4 s 沿长轴平动位移 (r//), 沿短轴平动位移 (r⊥) 和转动位移 (θ) 的非高斯参量Fig. 6. The non-Gauss parameter of the displacement of ellipsoid for lag time of 4 s: Translational displacement along the long axis of the ellipsoid (r//), translational displacement along the short axis (r⊥), and rotational displacement (θ).

4 总 结

利用摄像显微技术研究了椭球粒子在胶体圆球体系中的扩散行为. 通过对椭球粒子动力学行为的分析, 包括运动轨迹、均方位移、范霍夫自关联函数以及非高斯参量, 揭示了其在不同圆球浓度受限条件下的扩散行为演化. 结果表明, 随着圆球浓度的增大, 椭球粒子的平动和转动都变慢, 并且平动和转动在高浓度下变化不一致, 发生解耦合行为. 对于不同圆球浓度, 椭球表现出各向异性的扩散行为, 即趋向于沿椭球长轴方向扩散. 因此随着圆球浓度的增大, 沿长轴方向的平动会受到很强的受限, 其位移出现非高斯行为并逐渐增强; 而沿短轴方向的平动受到的影响较小, 其位移分布一直接近高斯行为. 这说明这两种平动行为随着圆球浓度的增大也发生了解耦合. 此外, 椭球转动位移的非高斯行为在高浓度会减弱, 与两种平动扩散都不一样, 进一步说明了椭球粒子在受限条件下平动和转动发生解耦合. 本文研究揭示了圆球受限对椭球粒子扩散动力学行为的重要影响, 有助于深入理解复杂微环境中各向异性粒子的运输和传递.