基于机器学习构建的环三亚甲基三硝胺晶体势*

王鹏举 范俊宇 苏艳 赵纪军

(大连理工大学, 三束材料改性教育部重点实验室, 大连 116024)

环三亚甲基三硝胺(RDX)是一种高能低感度炸药, 对其能量和性质的准确计算对于开展该炸药的分子模拟至关重要. 本文基于机器学习算法, 采用高维神经网络模型, 对RDX 分子晶体结构数据集进行势函数训练. 分别采用9 种不同的网络结构进行测试训练, 并选取其中学习效果最好的势函数对RDX 分子晶体结合能和晶格中原子受力进行计算, 均能很好地重复出第一性原理的计算结果, 其测试集结合能的均方根误差为59.2 meV/atom. 作为机器学习势函数的应用, 进一步使用该势函数对a 相RDX 晶体进行分子动力学模拟,以验证其适用性.

1 引 言

含能材料通常是由C, H, N 和O 四种元素在一定条件下形成的分子晶体, 可在短时间内释放出巨大能量, 被广泛地应用于常规武器装备的发射药、推进剂、炸药以及火工烟火药剂等[1]. 典型的含能材料有三硝基甲苯(C7H5N3O6, TNT)、环三亚甲基三硝胺(C3H6N6O6, RDX)、环四亚甲基四硝胺(C4H8N8O8, HMX)等. 其中, RDX 俗称黑索金,是一种常见的含能材料, 因其具有较好的热稳定性、高能量和高爆速等特点, 常用于各种军用炸药和推进剂. 目前, 已知的RDX 晶体共有五种晶型,分别为a,β,γ,δ和ε相. 其中,a相是常温常压相;β相为亚稳相[2−7], 在477 K 时可发生a到β相的相变[2];γ和δ相为高压相, 分别在约4.0 和18.8 GPa下出现[8−14], 但δ相至今并没有人得到其准确结构;ε相为高温高压相, 出现的温度和压强分别为489 K和4.2 GPa[15].

含能材料的起爆过程是一个涉及高温和高压等极端条件的瞬态过程, 许多现象和细节仍然无法在实验上直接获得. 计算模拟研究因具有周期短、成本小和安全等特点被广泛用于获取含能材料的基本性质、状态方程和爆轰性能等. 相比于第一性原理计算所需求的大量时间和计算资源, 经验势常被应用于含能材料的理论研究. 为获取含能材料晶体的基本性质, Sorescu 等[16]首先针对a相RDX晶体发展了一种分子间相互作用势用于结构和性质的描述. 将该势函数与晶格堆垛计算结合,得到的晶体结构和晶格能都与实验符合较好. 随后, 他们又将这种相互作用势用于30 多种其他硝铵分子晶体的预测, 发现当原子使用包含电子关联效应的第一性原理计算的电荷时, 大部分体系结构与实验相一致, 但晶格能有较大差异, 并通过给这些原子电荷量乘以一个尺度因子, 来降低这种差异[17].

相较于静态计算模拟, 分子动力学模拟不仅能计算不同温度、压力下含能材料的基本性质, 还能观测到一定条件下的分解过程. 常见的用于分子动力学模拟的经验势有Lennard-Jones 势[18]、CHARMM 势[19,20]、Compass 势[21]等. Liu 等[19]使 用CHARMM 力场对液态硝基甲烷进行分子动力学模拟. 结合Murnaghan 状态方程, 其体弹性模量和一阶导数计算结果与实验符合很好[22], 而通过Hogoniot 曲线计算得到的压力却高于实验值. 因传统经验势依赖于体系中已存在的化学键, 无法对旧化学键的断裂和新化学键的生成进行较好描述,Strachan 等[23]使用ReaxFF 反应力场[24]研究RDX在冲击波下的分解过程, 发现低冲击波速(< 6 km/s)下, RDX 分子中的N—N 键断裂为起始分解的主导过程, 随着波速增加和时间推移, N2和OH 成为主要产物. 此后, 人们不断优化ReaxFF 力场参数,并研究撞击等条件[25,26]对含能材料的影响. 鉴于现有经验势的参数对体系具有较强的依赖性, 其可移植性较差, 需要更加泛用的势函数来对含能材料进行准确描述.

近年来, 机器学习方法在物理和材料等领域得到了广泛的应用[27]. 通过大量的实验或计算得到的数据, 机器学习方法可以构建从结构、能量到性质的直接映射关系, 从而直接预测未知体系的性质, 以节省第一性原理计算所需要的大量计算时间.目前常见的机器学习算法有人工神经网络(ANN)[28]、高维神经网络(HDNN)[29]、库仑矩阵[30]、高斯近似势(GAP)[31]和核岭回归(KRR)[32]等方法. 针对分子体系, 通常使用这些方法对有机分子[30,33,34]、芳香族化合物分子晶体[35]以及分子团簇[36]等进行了大量研究, 并构建了可以准确地描述体系能量和性质的势函数. 此外, Elton 等[37]使用多种机器学习方法对不同含能材料分子的爆压和爆速等性质进行预测, 其结果均与实验结果相近. 基于此, 我们将机器学习方法用于含能材料RDX 晶体的研究, 采用Behler 和Parrinello[29]提出的HDNN 方法, 对第一性原理计算得到的15199 个RDX 晶体结构进行势函数拟合, 并对不同神经网络结构所拟合得到的势函数进行评估. 通过对大量RDX 晶体数据集的学习和机器学习模型的参数拟合, 以期获得可以准确描述晶体中分子内和分子间相互作用的势函数, 为不同RDX 晶型能量和性质的准确计算提供新的研究方法.

2 研究方法

2.1 数据集获取

首先, 使用Monte Carlo 和模拟退火算法[38,39]结合Mors6-SCFF 力场[40]对RDX 晶体进行结构搜索, 以期在已知的a,β,γ和ε相之外得到更多的稳定晶型, 模拟晶胞中均包含8 个RDX 分子.之 后,使 用VASP (Viennaab-initiosimulation package)[41]软件包对搜索得到的晶型进行结构优化. 选取广义梯度近似(GGA)下的PBE (Perdew-Burke-Ernzerhof)[42]泛函和缀加平面波(PAW)[43],能量截断为1000 eV,k点设置为2 × 2 × 2. 优化后共得到248 种不同的RDX 晶型结构.

为获取更多的数据进行训练, 继续对这248 种结构进行加压优化、改变晶格参数、二面角大小、斜切以及对部分原子位移等操作产生新的结构, 并使用上述相同的设置进行能量和原子受力计算. 剔除部分不合理的结构后, 最终得到15199 个用于训练的结构.

2.2 机器学习模型构建

使用HDNN[29]模型在aenet (atomic energy network)[44,45]软件包进行机器学习计算. 这种方法对体系中每一个原子的能量进行单独计算, 所有原子能量的加和为体系的总能量. 因此, 首先通过每个原子和周围不同种类原子的位置关系来构建基函数[29], 公式如下所示:

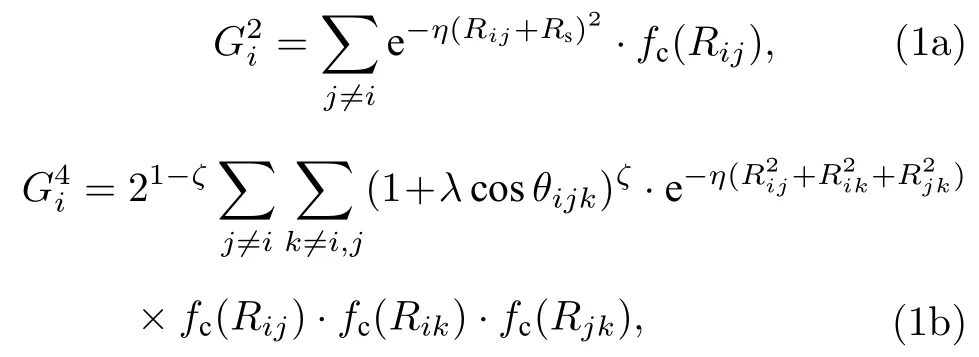
其中i,j和k代表不同原子;Rij,Rik和Rjk代表原子间距离;θijk为i,j,k三个原子连线的夹角.Rs为偏移参数, 取值为0. (1a)式中的η和(1b)式中的ζ,λ,η为可调节参数, 取值如表1 和表2 所列.fc为平滑截断函数, 表达式为[29]:

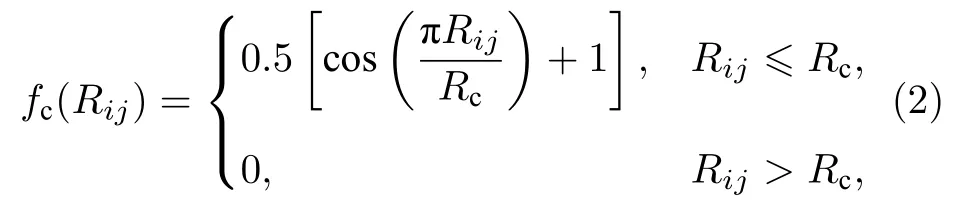
Rc为截断距离, 在本文中设置为6.5 Å. 因RDX晶体中有H, C, N 和O 4 种原子, 对于(1a)式中的每一种η的取值, 有4 个不同的基函数, 而对于(1b)式中每一组参数取值, 会有10 个不同的基函数. 因此, 对于每一种原子, 共得到72 个基函数结果作为输入层神经元. 隐藏层的层数和每层神经元的个数是神经网络结构的超参数, 需要手动调整来获得最佳学习效果. 因此, 我们分别采用双隐层

(10-10, 20-20, 30-30), 三隐层(10-10-5, 20-20-10,30-30-10)和四隐层(10-10-10-5, 20-20-10-10, 20-20-20-10)共9 种隐藏层结构进行神经网络构建.输出层只包含一个神经元, 代表该原子的能量, 所有原子能量加和为体系总能量, 其表达式为[46]

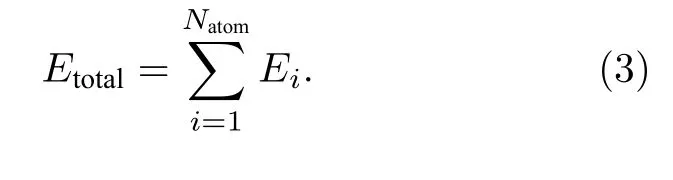
表1 4×3 个G2 型径向基函数((1a)式)中η 取值Table 1. η of 4 × 3G2 type radial basis functions(Eq. (1a)).

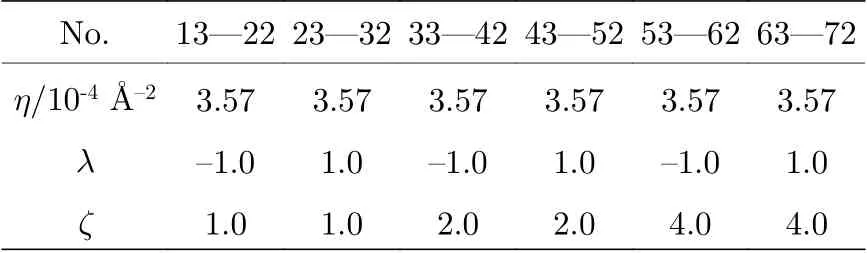
表2 10 × 6 个G4 型角向基函数((1b)式)中η,λ, ζ 取值Table 2. η, λ, and ζ of 10 × 6 G4 type angular basis functions (Eq. (1b)).

原子在一个方向上的受力可以写为总能量对该方向位移偏导的相反数, 表达式为[46]

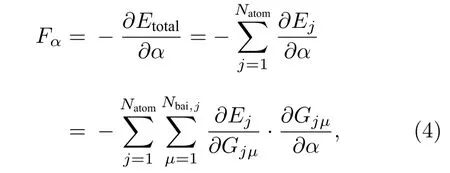
其总体神经网络结构如图1 所示.

对于隐藏层神经元, 激活函数选择的是线性弯曲的双曲正切函数, 其表达式为[47]

对于每一种隐藏层网络结构所对应的神经网络, 分别随机选取90%数据集(即13680 个)作为训练集进行最多2000 代误差反向传播学习[48], 对神经网络中的连接权重和偏置进行更新优化, 以期使误差达到最小, 其余10%的数据集(即1519 个)作为测试集来评估训练得到的势函数效果.

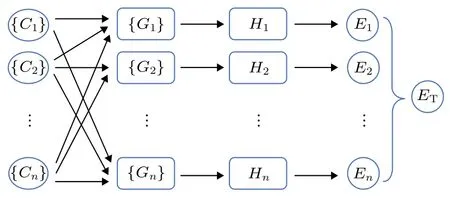
图1 高维神经网络结构示意图, C代表原子坐标, G 代表基底函数, H 代表隐藏层神经元, E 代表原子能量, 下角标1, 2, ···, n 为原子序号, ET 为体系总能量Fig. 1. Structure of high-dimensional neural network. C, G,H, and E represent coordinates of atom , basis functions,hidden layer neurons, and energy of atom , respectively.Subscripts, 1, 2, ···, n are the serial numbers of atoms, and ET is the total energy of the system.

进一步, 使用机器学习所得到的势函数对2 ×2 × 2 晶胞的a相RDX 晶体进行分子动力学模拟计算. 模拟计算应用LAMMPS (large-scale atomic/molecular massively parallel simulator)[49]软件包,使用麦克斯韦-玻尔兹曼分布进行速度初始化, 时间步长设置为0.2 fs, 在300 K 温度及13194.4 Å3体积(对应密度为1.79 g/cm–3)条件下进行正则系综(NVT)模拟, 模拟时长为20 ps.

3 结果与讨论

3.1 势函数训练

图2 为a相RDX 晶体结构和4 种常见RDX分子构型示意图.a相RDX 是在常温常压下稳定存在的晶型, 最易在实验上观测到, 其单胞中含有8 个RDX 分子, 空间群为Pbca[2,3,7]. 同时, 根据硝基与三嗪环轴线夹角的不同, RDX 分子有AAA,AAE, AEE 和EEE 四种常见构型, 如图2(b)所示, 其中, 在a相中RDX 分子为AAE 构型[10].

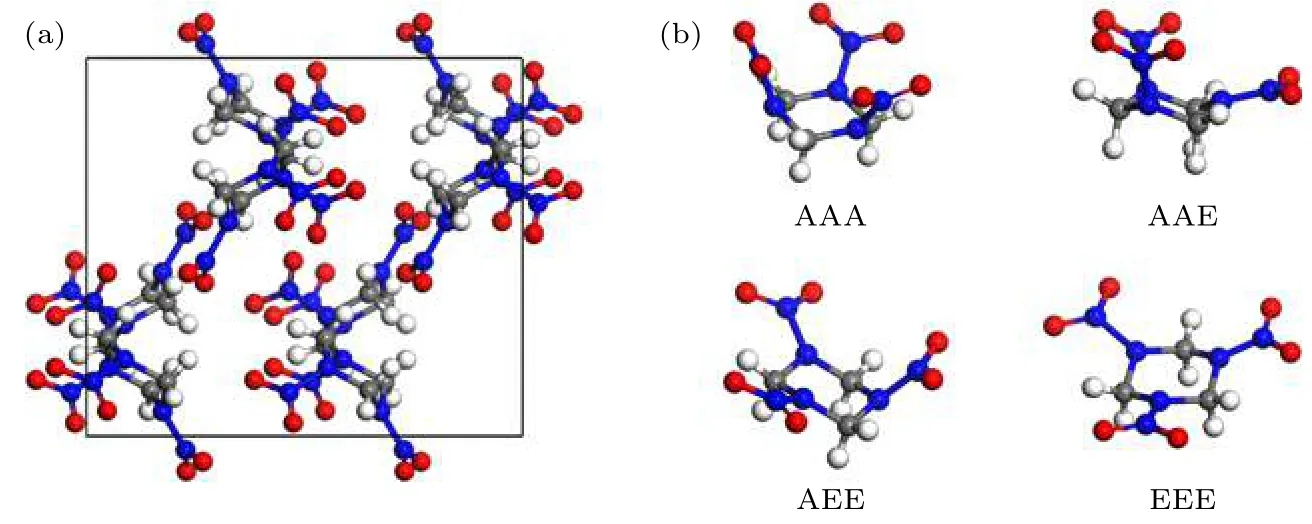
图2 (a) a 相RDX 晶体结构示意图; (b) 4 种常见RDX 分子构型示意图[10], 白球代表氢原子, 灰球代表碳原子, 蓝球代表氮原子, 红球代表氧原子Fig. 2. (a) Structure of a-RDX crystal; (b) structures of four usual types of RDX molecules.[10] The white, grey, blue, and red balls represent hydrogen, carbon, nitrogen, and oxygen atoms, respectively.

图3 (a) 9 种隐藏层结构在400 代之后测试集最低RMSE 随迭代步数变化示意图; (b) 30-30-10 隐藏层网络结构在1500 代之后训练集和测试集RMSE 随迭代步数变化示意图Fig. 3. (a) Diagram of test set lowest RMSEs variation along with training iteratons of nine types hidden layer neural structures after 400 iterations; (b) diagram of training and test sets RMSEs variation along with training iteratons of 30-30-10 hidden layer neural structures after 1500 iterations.

目前所确知的RDX 晶型只有a,β,γ和ε相4 种, 而机器学习尤其是神经网络模型需要大量的数据来训练. 因此, 首先进行RDX 晶体结构搜索,随后对搜索得到的结构使用改变晶格参数和斜切等方法产生大量新结构并计算其能量和原子受力,共获取15199 个结构用于训练势函数以及对训练效果进行评估. 采用Behler 等[29]提出的HDNN方法, 如图1 所示, 即对每一个原子采用(1a)式和(1b)式两种共72 个基函数, 通过周围原子环境构建输入层神经元, 其参数选取如表1 和表2 所列. 隐藏层分别采用9 种不同的网络结构. 输出神经元为该原子的能量, 所有原子能量加和为体系总能量.

为了找到最适于描述RDX 晶体势函数的网络结构, 对于9 种不同的隐藏层结构所对应的神经网络, 进行最多2000 代的误差反向传播学习[48],并使用测试集的均方根误差(RMSE)对训练效果进行评估. 图3(a)为400 代后9 种网络结构的测集的最小RMSE 随迭代步数的变化图. 由图3(a)可以看出, 30-30-10 隐层结构在1268 代后具有最低的RMSE, 说明30-30-10 隐层网络结构训练得到的势函数对能量的计算相比于第一性原理误差最小, 更加适合于对RDX 晶体的描述.

图3(b)是1500 代后30-30-10 隐藏层网络结构的训练集和测试集RMSE 随迭代步数变化示意图. 由图3(b)可以看出, 这一阶段训练集的RMSE随迭代步数近似线性下降, 而测试集的RMSE 随迭代步数增加无明显变化趋势, 其最低点出现在1847 代, RMSE 为59.2 meV/atom, 即图中两条蓝色虚线交点处. 在1847 代后, 测试集的RMSE 上升,而训练集的RMSE 继续下降, 说明此时对势函数的训练出现了过拟合. 因此, 选取第1847 代训练后所得到的势函数进行后续的计算, 此时训练集的平均绝对误差(MAE)为29.2 meV/atom, RMSE 为47.1 meV/atom, 测试集MAE 为35.1 meV/atom,RMSE 为59.2 meV/atom.

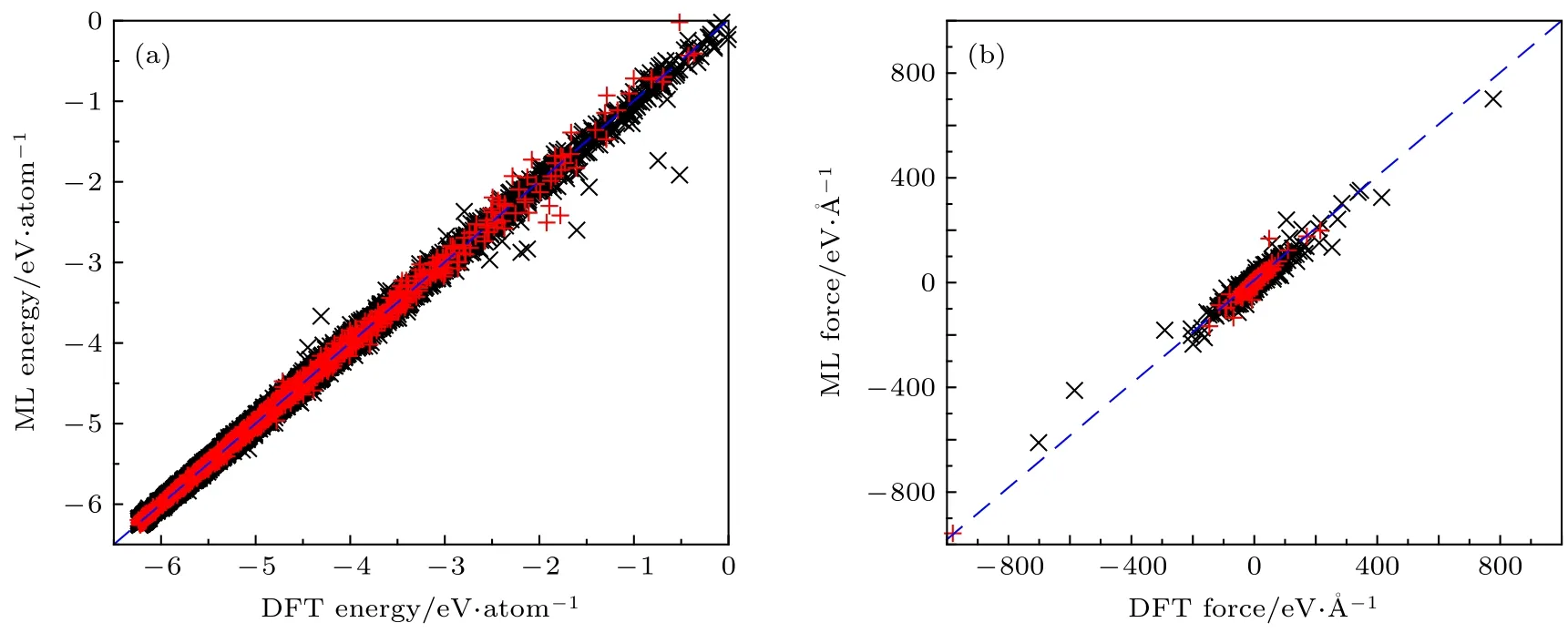
图4 (a) 训练集(黑色叉)和测试集(红色十字)所有结构第一性原理计算形成能和机器学习计算形成能对应关系图; (b) 训练集(黑色叉)和测试集(红色十字)所有结构第一性原理计算原子受力和机器学习计算原子受力对应关系示意图Fig. 4. (a) Correlation of machine learning binding energies with the corresponding ab initio reference energies for all structures in the training (black skew crosses) and testing (red crosses) sets; (b) correlation of machine learning atomic forces with the corresponding ab initio reference forces for all structures in the training (black skew crosses) and testing (red crosses) sets.

使用此势函数对包括训练集和测试集所有的15199 个结构进行能量和晶胞中原子受力的计算,其结果与第一性原理计算结果对比如图4 所示,MAE 与RMSE 列在表3 中. 图4(a)为第一性原理计算结合能和机器学习势函数计算形成能的对应关系图, 图中蓝色虚线代表第一性原理计算能量和机器学习计算能量相等, 数据点离蓝色虚线越近说明计算误差越小. 由图4(a)可以看出, 除个别结构外, 绝大多数数据点都在蓝色虚线附近, 说明该势函数可以很好地重复出第一性原理计算所得到的结合能, 而且训练集和测试集在虚线两侧分布均匀, 比例大致相当, 说明数据集的选取具有代表性.图4(b)为第一性原理计算晶胞中原子受力和机器学习计算原子受力的对应关系示意图. 因每个原子有x,y,z三个方向的受力, 每个结构晶胞中有168 个原子, 计算所得的原子受力过多, 无法在一张图中做出, 这里对每一个结构随机选取了一个原子在一个方向上的受力, 做出此示意图. 由图4(b)可以看出, 图中所有数据点都在蓝色虚线附近,而且几个受力极大(> 200 eV/Å)的原子, 机器学习势函数的计算结果也和第一性原理计算结果相近. 如表3 所列, 与第一性原理计算相比较,训练所得到的势函数不仅能较好得计算晶体能量信息, 同时也能得到可信的原子受力信息, 说明该势函数适用于对不同晶型的RDX 晶体能量与受力描述.

为验证势函数对已知结构计算的可靠性, 对于a,β,γ和ε四种晶型, 使用VASP[42]软件包,在0 K温度下分别在标准大气压到6 GPa 以1 GPa 为间隔, 共7 种压强条件下进行结构优化并对其能量和原子受力进行计算, 进而使用机器学习所得的势函数对其结合能和原子受力进行计算, 并与之比较, 其结合能对比结果如图5 所示. 可以看出, 能量误差最大的结构为γ相在1 和2 GPa 条件下的结构, 此时机器学习势函数所计里算结合能较第一性原理所计算结合能低20.1 meV/atom,其余26 种结构的绝对误差均小于20 meV/atom.对于这28 种结构, 结合能的MAE 为8.8 meV/atom,RMSE 为10.0 meV/atom, 原子受力的MAE 为0.88 eV/Å, RMSE 为1.11 eV/Å, 均远小于训练集和测试集的结合能和原子受力的MAE 和RMSE(如表3 所列), 说明对于已知稳定结构, 机器学习势函数的计算效果优于对于随机不稳定结构的计算, 因此可将该势函数用于对更多未知的稳定结构的预测.

表3 训练集与测试集机器学习计算形成能和原子受力与第一性原理计算比较MAE 和RMSETable 3. MAE and RMSE of machine learning binding energies and atomic forces corresponding ab initio reference energies and forces in the training and test sets.

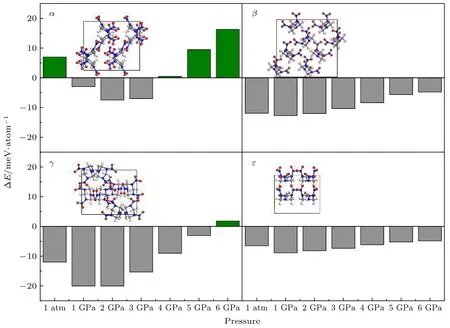
图5 0 K 下4 种已知RDX 晶型在标准大气压到6 GPa 压强下机器学习计算结合能的误差Fig. 5. Errors of machine learning binding energies of four known RDX crystals from 1 atm to 6 GPa at 0 K.

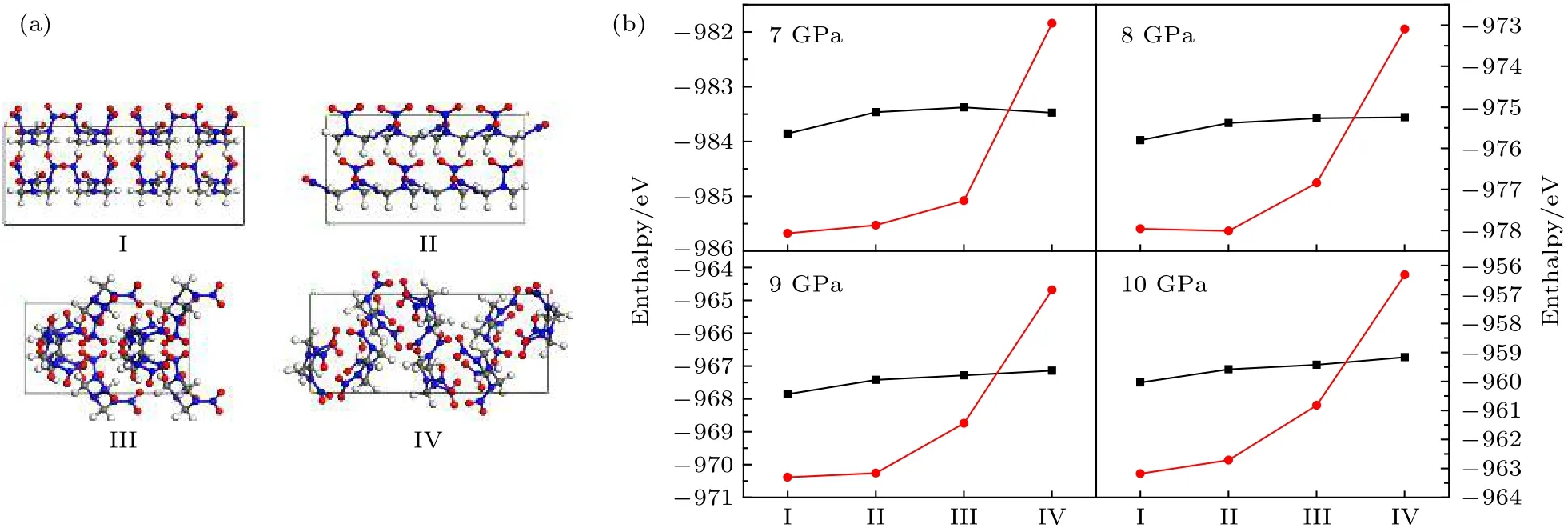
图6 (a) 4 种RDX 晶型结构示意图; (b) 7—10 GPa 下4 种晶型第一性原理计算(黑色方块)和机器学习势函数计算(红色圆圈)的焓值Fig. 6. (a) Structures of four RDX crystals; (b) enthalpies from 7 to 10 GPa calculated by ab initio (black block ) and machine learning potential (red circle).

因存在实验上观测到而理论上未确定具体结构的高压RDX 晶型, 我们在搜索到的248 种构型中选取了4 种能量较低的晶型, 其结构如图6(a)所示. 对这4 种晶型分别在7—10 GPa 四种压强条件下优化, 并使用VASP[42]软件包和训练得到的势函数进行焓值计算, 其结果如图6(b)所示. 由图6(b)可以看出, 在4 种压强条件下, 机器学习势函数均能给出与第一性原理计算相近的能量排序,焓值的RMSE 为13.7 meV/atom, 与已知结构能量的RMSE 相近, 进一步证明了该势函数对RDX分子晶体能量描述的准确性.

3.2 分子动力学模拟

为了考察该势函数的泛用性, 使用机器学习所得势函数对a相RDX 晶体的2 × 2 × 2 晶胞进行分子动力学模拟. 模拟的时间步长设置为0.2 fs,总时长为20 ps, 在300 K 温度及不同体积条件下进行NVT 系综模拟. 在13194.4 Å3体积(对应密度为1.79 g/cm3)下,其温度和压强随时间变化如图7 所示.由图7(a)可知,在1 ps之前,体系温度较高, 而在1.0—2.5 ps之间, 温度的波动较大, 2.5 ps之后温度在300 K附近平稳波动.由图7(b)可知,在2.5 ps之前,压强的波动幅度较大,在2.5 ps之后压强平稳波动,其平均压强为4.63 GPa.由此说明,体系在2.5 ps之前为体系弛豫过程,结构发生一定程度上的变形和重构,在2.5 ps之后,结构稳定,原子均在分子的平衡位置附近做规律运动.上述结果表明,该势函数可以较好地模拟分子内和分子间相互作用, 初步了证明其在分子模拟中的适用性.

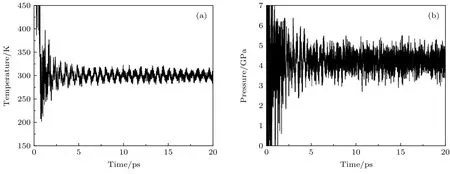
图7 (a)a 相RDX 2×2×2晶胞在NVT系综下分子动力学模拟温度随时间变化图;(b)压强随时间变化图Fig.7.Variations in time of the tem perature (a)and pressure(b)in the NVT ensem ble for 2×2×2 a-RDX crystal.

4 结论

本文采用HDNN[29]方法,对15199个RDX分子晶体结构数据集进行机器学习训练并得到相应的势函数.通过对9种不同隐藏层结构的神经网络进行最多2000代误差反向传播训练[48],并对其训练效果进行评估,选取测试集结合能RMSE最低的30-30-10隐藏层结构神经网络模型的训练所得势函数.相较第一性原理计算结果,机器学习拟合的势函数所计算的结合能和原子受力的误差如表3所列,均能很好地重复出第一性原理的计算结果.使用该势函数对4种已知晶型的RDX晶体在不同压强条件下计算结合能并与第一性原理计算结果相对比, 其结合能RMSE仅为10.0 meV/atom,原子受力RMSE为1.11 eV/Å,说明该势函数对于已知稳定结构的计算更加合理.

进一步,使用训练得到的势函数对a相RDX晶体的2×2×2晶胞在NVT系综下进行分子动力学模拟,发现其温度和压强在2.5 ps后波动稳定,证明该势函数对分子内和分子间相互作用均能较好地描述.本文针对含能材料RDX 晶体进行机器学习势函数的构建,为今后分子晶体方向的机器学习研究提供帮助和启示.

感谢北京计算科学研究中心管鹏飞研究员、北京应用物理与计算数学研究所宋华杰研究员的帮助,以及大连理工大学超级计算中心提供的计算支持.