基于超表面的旋向选择吸波体*

王朝辉 李勇祥 朱帅

(空军工程大学防空反导学院, 西安 710051)

近年来, 基于超表面的完美吸波体成为了各国学者的研究热点. 其中圆极化波的旋向选择吸波体更是在手性传感器和卫星通讯等领域有着广泛的应用. 为此, 本文提出了一种基于方形开口环结构超表面的圆极化波的旋向选择吸波体. 该吸波器能够吸收入射的右旋圆极化波, 而完全反射左旋圆极化波. 首先从理论上分析产生旋向选择吸波的理论条件, 然后在该理论的指导下设计出了符合条件的超表面单元. 该单元由金属-介质板-金属三层构成, 顶层是改进后的方形开口环金属结构, 中间层是FR4 介质板, 底层是全金属板. 对超表面单元进行数值仿真, 仿真结果表明, 该单元在7.2 GHz 处可以选择性吸收右旋圆极化波而反射左旋圆极化波, 并且保持圆极化波的旋向不改变. 右旋圆极化波的吸波率达到了90%以上, 而左旋圆极化波的吸波率低于19%. 该方法不仅适用于微波段, 而且可以被推广到更高频段, 有望在卫星通讯领域得到广泛应用.

1 引 言

完美吸波体是一种可以完全吸收入射电磁波的设备. 由于强大的吸波性能, 吸波体在发射器、传感器和隐身[1]等领域得到了广泛的应用. 传统的吸波体由自然材料组成, 如楔形吸波体和铁氧体[2,3].然而, 这种类型的吸波体有着体密度大、入射角度敏感和加工难度大的缺点, 严重限制了其在实际当中的应用.

近年来, 由亚波长人工结构周期排列组成的二维平面超表面成为研究热点, 因其具备强大的电磁操控能力和低剖面的优点. 具有各种功能的超表面陆续被提出[4−9], 如极化转换超表面[5]、涡旋波束产生超表面[6−8]、散射增强超表面[9]和反射聚焦超表面[10]等. 更重要的是, 自从第一个表现出优异性能的超表面吸波体被证明之后[11], 超表面在吸波领域的应用也受到了广泛关注. 目前, 基于超表面的吸波研究已经取得可观的进展, 各种性能的超表面吸波体被设计出来[12−21]. 2017 年, Cui 课题组[17]运用透明的铟锡氧化物(indium-tin-oxide,ITO)电阻薄膜实现了一个可以在8—18 GHz 频段内吸收率达到90%的宽带吸波体. Zhou 等[18]将吸波和极化转换功能整合在单一超表面上实现了多功能超表面. 随着超表面吸波体的深入研究,Li 等[19]通过构造旋转的“L”形金属线结构单元,设计和验证了一个可以工作在8.72 GHz 下的手性依赖超表面吸波体. 随后, 在THz 频段内相似的结构也被验证[20]. Shang 等[21]通过在圆形开口环加载电容, 设计出一个可以实现右旋圆极化波(righthanded circularly polarized waves, RCP)完全吸收而左旋圆极化波(left-handed circularly polarized waves, LCP)完全反射的旋向选择吸波器. 然而,这些旋向选择的手性吸波结构要么是通过在介质板打孔, 要么是通过加载电子元件来实现, 这不仅增加了加工的难度, 而且不易于应用在更高频段(THz, IR 和光波段).

鉴于以上问题，本文提出了一种基于超表面的旋向选择吸波体, 该吸波体不仅可以完全吸收入射的RCP 波, 完全反射LCP 波, 而且反射波的旋向保持不变. 仿真结果也进一步证明了该吸波体高效的旋向选择吸波性能. 圆极化波的旋向选择吸波体更是在手性传感器和卫星通讯等领域有着广泛的应用. 该设计方法简单易构, 不需要复杂的负载元件, 不仅适用于微波段, 而且可以很容易应用在到更高频段.

2 理论分析

根据文献[12]所述的旋向选择吸波理论, 当圆极化波垂直入射时, 反射矩阵R连接入射场和反射场, 如(1)式所示:

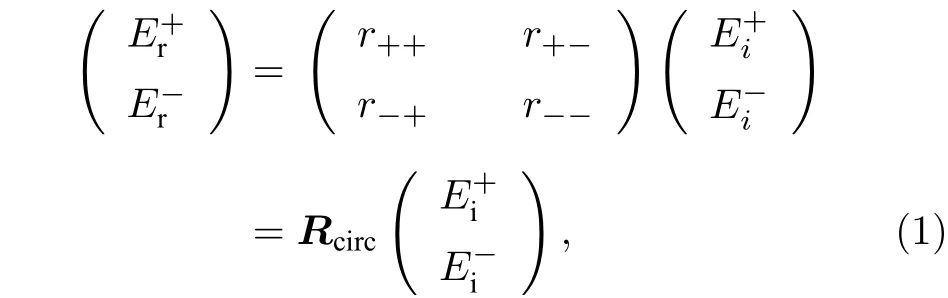
其中,Er和Ei代表LCP(–)和RCP(+)的反射场和入射场. “+”和“–”分别表示从+z方向观察时顺时针旋向圆极化波和逆时针旋向圆极化波.Rcirc代表着圆极化波的反射矩阵, 该矩阵可以被线极化波的反射系数所表示:

(2)式中下标“x”和“y”分别代表着x和y极化波.由于透射光和反射光的波矢量方向是相反的, 所以相比于透射, 每一个反射系数都有不同的物理含义. 例如,r++和r−+分别表示RCP 入射光的交叉和共极化反射系数. 假设入射波沿+z传播, 则可将反射系数定义为rLR=r++,rRR=r−+,rLL=r+−,rRL=r−−.

假设RCP 波被完全吸收, 而LCP 波被完全反射, 且旋向保持不变, 那么反射系数应该满足以下情况:r++=r−+=r−−=0 ,|r+−|=1 .

此时, 满足该种情况的惟一解是:

其中α是任意相移.

本文讨论了旋转对称和镜像对称两种情况下满足旋向选择吸波的条件. 通常情况下, 旋转对称结构满足以下条件[12]:

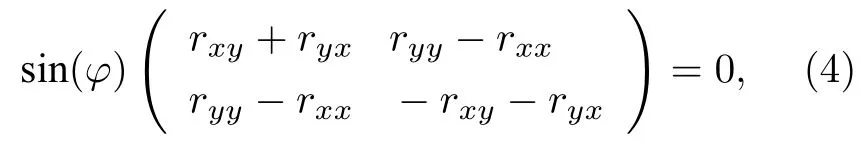
其中φ代表着单元绕z轴旋转一圈下来, 出现旋转后的结构与原始结构重合时的旋转角. 为了同时满足方程(3)和(4), 仅φ=mπ (m=0,±1,···)的旋转对称结构满足要求. 因为满足该要求的旋转对称结构旋转一圈下来, 只有两种情况会使旋转后的结构与原结构重合, 所以仅仅2 重旋转对称结构才能够实现预期的旋向吸波性能.

然而, 镜像对称结构满足的条件为[12]

根据(3)式可知,(rxx-ryy)/rxy的比值为一个纯虚数, 所以(5)式描述的镜像对称条件永远不可能被满足. 因此, 旋向选择吸波体不可能存在于镜像对称的结构当中.

经过以上的理论分析可得出实现旋向选择吸波的条件为: 结构必须同时打破n重(n> 2)旋转对称和镜像对称.

3 单元设计

根据以上理论分析的结论, 为打破n重(n> 2)旋转对称和镜像对称, 本文在原始开口环的基础上(如图1(a)和图1(b))提出了一个改进的方形开口环结构, 如图1(c), (d)所示. 该超表面单元由三层结构组成, 顶层是厚度为0.105 mm 的金属结构,中间层是FR4 介质板, 介电常数为4.2, 电正切损耗为0.025, 最底层为金属背板, 用来反射入射的电磁波. 该超表面工作在反射体系下, 优化后的结构参数为:p= 10 mm,a= 6.5 mm,g= 0.6 mm,w= 0.4 mm,l= 2 mm,d= 4 mm. 整个超表面单元的总体厚度为4.105 mm.

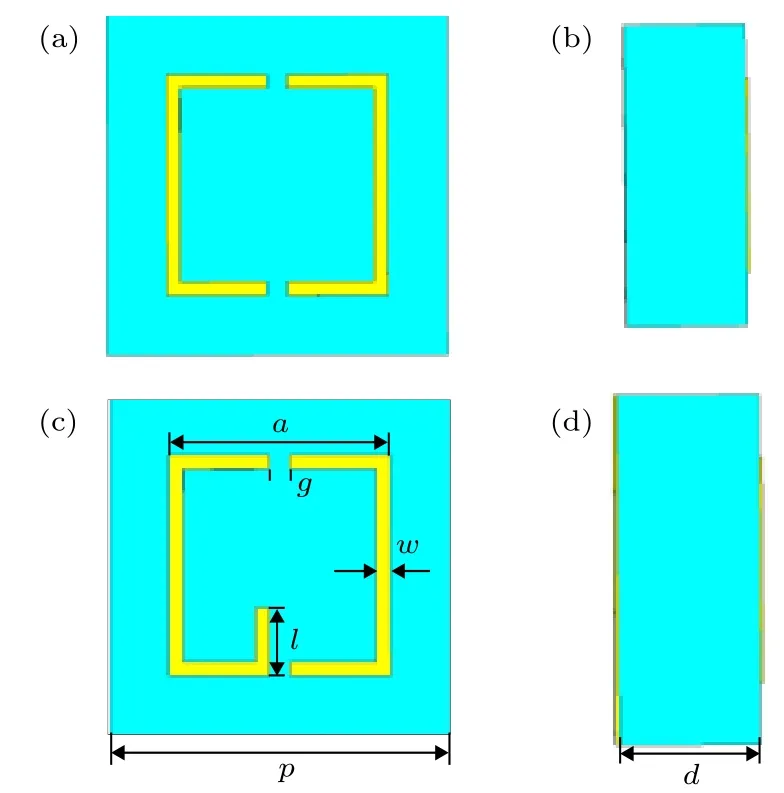
图1 单元结构示意图 (a), (c) 顶视图; (b), (d) 侧视图Fig. 1. Schematic of the unit cell: (a), (c) Top view; (b), (d) side view.

4 单元的仿真和实验验证

采 用CST MICROWAVE STUDIO (2018)软件对单元的反射系数进行仿真. 仿真的边界条件设置如图2(a)所示. 在x和y方向采用unit cell 边界条件, 由于单元工作于反射体系下, 所以在Zmin方向采用electric(Et= 0)边界条件, 而Zmax方向采用open(add space)边界. 整个仿真采用圆极化波进行激励, 仿真结果如图2(b)所示. 原始单元的边界条件和仿真结果如图2(c)和图2(d)所示.

从仿真结果可以看出, 原始的结构并不能产生理想的旋向选择吸波. 改进后的单元在7.2 GHz处, LCP 波的反射幅度(r+−)在0.9 以 上,而RCP 波的反射幅度(r−+)仅仅为0.2. 由此可知,该超表面不仅选择性地反射了LCP 波, 而且其旋向保持不变. 该功能可以看作一个圆极化器和滤波器的整合. 考虑到手性结构会存在交叉极化反射,因此, 单元整体的吸收率(A)简单定义为

式中R+−(R−+)表示交叉极化反射,R−−(R++)表示共极化反射. 计算的吸收率谱线如图3 所示.

从图3 可以清晰地看到, 在7.2 GHz 处RCP波的吸收率达到了90%以上, 而LCP 波的吸收率在19%以下. 这表明入射的RCP 波被高效地吸收, 而几乎所有的LCP 波被反射. 在实际的应用当中, 入射的电磁波往往以不同的角度斜入射在物体表面上, 因此讨论了单元对入射角度的敏感性.在这里分别研究了入射波矢在xoz和yoz平面内的斜入射吸波性能. 计算结果如图4 所示.

从仿真结果可以看出, 对于入射波矢在xoz面内的情况, 当入射角从0°变化到45°的时候, 虽然RCP 波的吸收率稍微有点降低, 但是仍然维持在了77%以上, 而LCP 波的吸收率在30%以下. 然而, 对于入射波矢在yoz面的情况, RCP 波的吸收率随着角度的增加而逐渐降低, 但是仍保持着60%以上的吸收率.

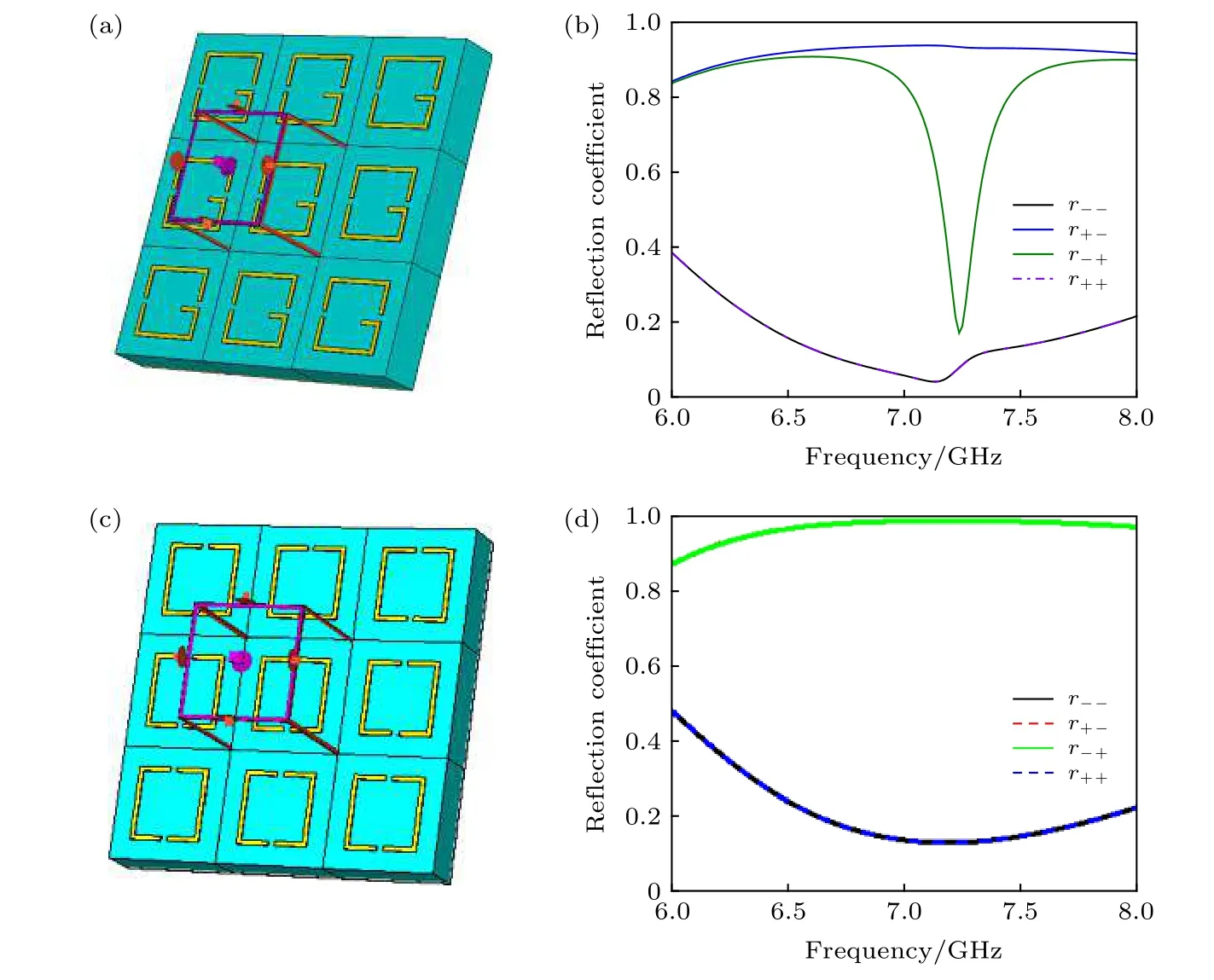
图2 仿真边界条件设置和反射系数仿真结果 (a), (c) 边界条件设置; (b), (d) 反射系数仿真结果Fig. 2. Setting of the simulation boundaries and the simulated results of reflection coefficient: (a), (c) Setting of the simulation boundaries; (b), (d) the simulated results of reflection coefficient.

图3 LCP 和RCP 波的吸收率谱线Fig. 3. The absorption spectra of LCP and RCP wave.

为进一步揭示物理机理, 对谐振频率7.2 GHz处超表面单元的表面电流和能量损耗分布进行仿真. 由于金属结构的非对称性, LCP 波和RCP 波将在结构表面引起不同的电流分布和能量损耗. 从图5 的仿真结果可以很清楚地看到, RCP 波入射能够引起很强的表面电流和能量损耗, 从而实现旋向选择吸波.

为了进一步证明该方案的可行性, 采用所设计的单元加工一个包含 2 0×20 个单元的超表面进行实验验证. 样品的实物图和测试环境如图6所示.

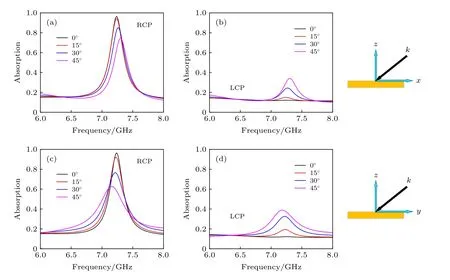
图4 两种不同情况下不同入射角度的LCP 和RCP 波的吸收率谱线 (a), (c) RCP 波吸收谱线; (b), (d) LCP 波吸收谱线Fig. 4. The absorption spectra of LCP and RCP wave under different incident angles with the wave vectors confined in the x-z plane and y-z plane, respectively: (a), (c) The absorption spectra of LCP wave; (b), (d) the absorption spectra of RCP wave.

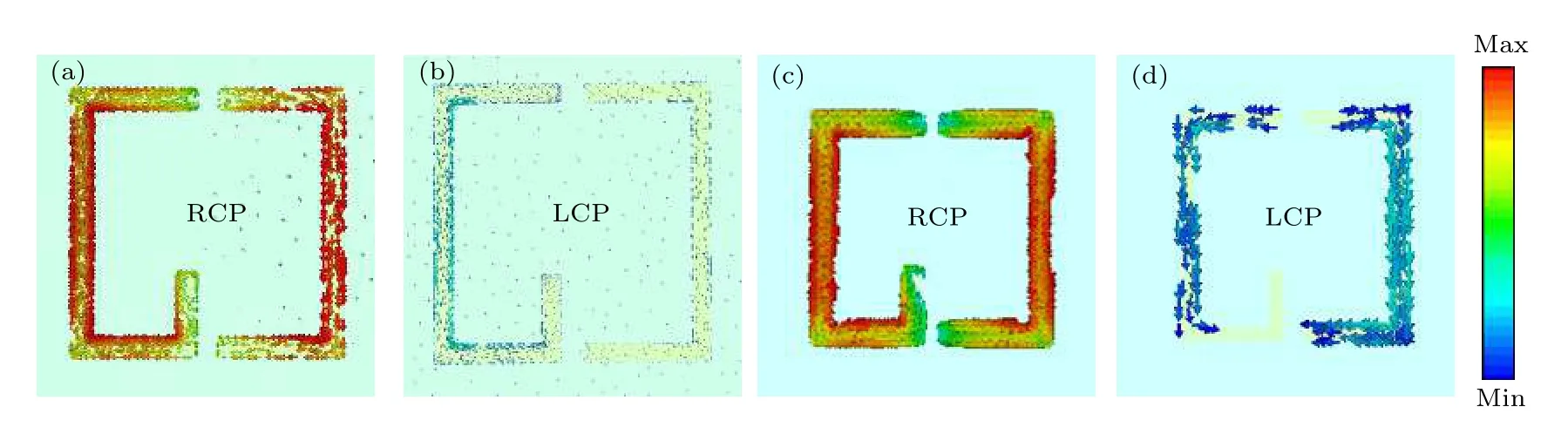
图5 在谐振频率7.2 GHz 处的表面电流和能量损耗密度分布 (a)右旋波圆极化波入射下电流分布; (b)左旋圆极化波入射下电流分布; (c)右旋圆极化波入射下能量损耗; (d)左旋圆极化波入射下能量损耗Fig. 5. Surface current distributions on the unit cell at 7.2 GHz: (a) Surface current under the incidence of RCP wave; (b) surface current under the incidence of LCP wave; (c) energy loss under the incidence of RCP wave; (d) energy under the incidence of LCP of wave.

图6 (a)超表面样品; (b)测试环境设置Fig. 6. (a) Fabricated prototype of the proposed metasurface; (b) experimental setup.

图7 两种不同情况下对于不同入射角度的LCP 和RCP 波的仿真和测试的吸收率谱线 (a), (c) RCP 波吸收谱线;(b), (d) LCP 波吸收谱线Fig. 7. The simulated and measured absorption spectra of LCP and RCP wave under different incident angles with the wave vectors confined in the x-z plane and y-z plane, respectively: (a), (c) The absorption spectra of LCP wave; (b), (d) the absorption spectra of RCP wave.

如图6(b)所示, 在测试的过程中, 将两个工作在4—8 GHz 的圆极化喇叭作为发射和接收天线连结在矢量网络分析仪的两个端口上. 喇叭与样品之间的距离满足远场条件, 确保入射在样品表面的电磁波为平面波. 图7 呈现了测试和仿真结果的对比.

从图7 的结果中可以看出, 测试结果和仿真结果几乎是一致的, 微小的偏差主要是样品加工过程中不可避免的误差.

所设计的单元不仅可以在微波段实现旋向的选择吸波, 而且可以很容易地扩展到高频段. 将结构参数降低到微米级别进行了如图8 所示的THz 频段仿真. 具体的结构参数如下:p= 10 µm,a= 6.2 µm,g= 0.6 µm,w= 0.4 µm,l= 2 µm,d= 2.5 µm. 仿真结果表明, 在15.5 THz 处右旋波达到了90%以上的吸收率, 而左旋波吸收率不足20%, 这充分证明了该方案可以很容易扩展到高频段的可行性. 接下来, 将本文结果与近年来的工作进行对比, 对比结果如表1 所列. 从表1 中可以看到, 本文的方法在吸收率和入射角度方面表现出了较优异的性能.

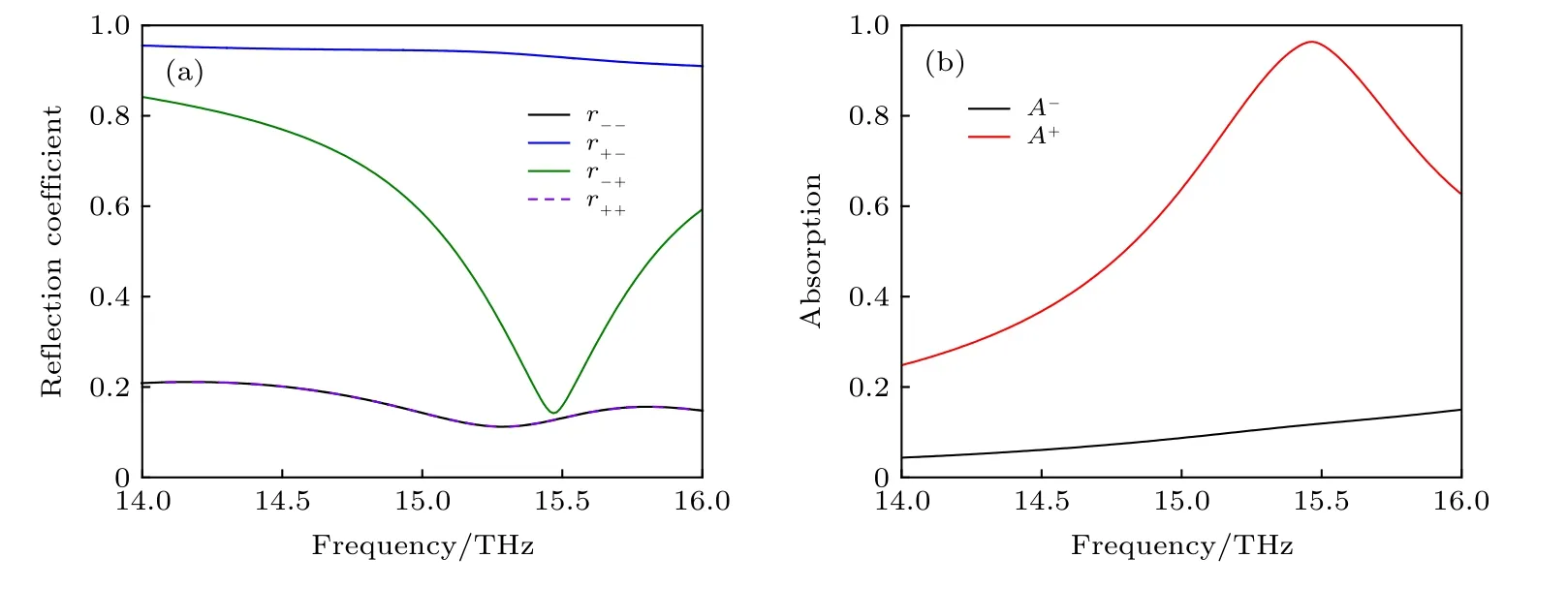
图8 在THz频段反射系数和吸收率谱线仿真结果(a)反射系数;(b)吸收率谱线Fig.8.The simulated results of reflection coefficient and absorp tion spectra at frequency band of THz:(a)The reflection coefficient;(b)the absorption spectra.

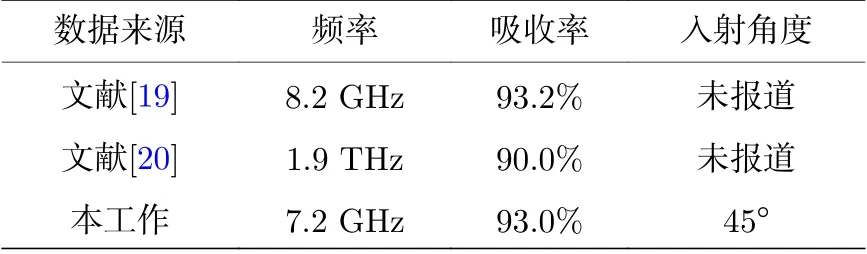
表1 不同方法的对比Table 1.The comparison of different approaches.

5 结 论

本文提出了一种基于改进后的方形开口环单元结构超表面产生圆极化波旋向选择吸波的方法.该单元结构同时打破了n重(n>2)旋转对称和镜像对称,满足了产生旋向选择吸波的理论条件.仿真结果也表明,该超表面能够在7.2 GHz处实现右旋圆极化波的吸收和左旋圆极化波的反射,而且不改变反射波的旋向.右旋圆极化波的吸收率在谐振频率处达到了90%以上,而左旋圆极化波的吸收率仅仅在19%以下.该方法不需要加载任何电子元件,克服了以往方法加工难度大的难题,有望在手性传感器和卫星通讯等领域得到广泛的应用,甚至可以被推广到更高频段.