稳定广义低秩矩阵逼近算法
史加荣 米合拉衣·阿地勒
1(西安建筑科技大学省部共建西部绿色建筑国家重点实验室 陕西 西安 710055)2(西安建筑科技大学理学院 陕西 西安 710055)
0 引 言
在模式识别、机器学习和计算机视觉等领域中,通常假设数据集存在于单个或多个低维线性子空间中。矩阵分解正是利用数据集的近似低秩结构来恢复低秩成分、移除噪声和补全缺失值[1]。对于灰度图像集等二维数据集,在使用传统的主成分分析(Principal Component Analysis,PCA)、奇异值分解(Singular Value Decomposition,SVD)和线性判别分析(Linear Discriminant Analysis,LDA)等子空间学习方法时,需要先将矩阵拉伸为向量,这种向量化破坏了数据本身的空时结构,也可能会导致小样本问题和维数灾难[2]。为此,许多一维子空间方法相继被推广到二维情形,例如:二维PCA[3]、二维SVD[4]、二维LDA[5]、双向二维PCA[6]和广义低秩矩阵逼近[7]等。
与SVD相比,GLRAM具有更好的压缩性能和较低的计算量,已成为处理二维数据集的一种重要方法。Liu等[8]揭示了GLRAM与SVD的关系,讨论了GLRAM目标函数的下界。赵扬扬等[9]提出了求解GLRAM的非迭代算法;Shi等[10]基于GLRAM提出了求解矩阵补全问题;Ren等[11]使用GLRAM构造了一个统一的网络来学习高维映射;Luo等[12]将GLRAM和随机低秩矩阵逼近应用到视频处理中;张长伦等[13]建立了GLRAM的一个改进模型。当数据集受到大的噪声腐蚀时,GLRAM可能不再奏效。为此,Shi等[14]提出了鲁棒GLRAM(Robust GLRAM, RGLRAM),随后Wang等[15]把秩最小化引入到鲁棒模型中。尽管RGLRAM在图像恢复和视频背景建模中取得了良好的效果[14-16],但该模型没有考虑高斯噪声腐蚀和数据缺失情形。基于此,本文提出RGLRAM的一个新版本,即稳定广义低秩矩阵逼近。
1 相关工作
1.1 广义低秩矩阵逼近

Di=LMiRT+Eii=1,2,…,N
(1)
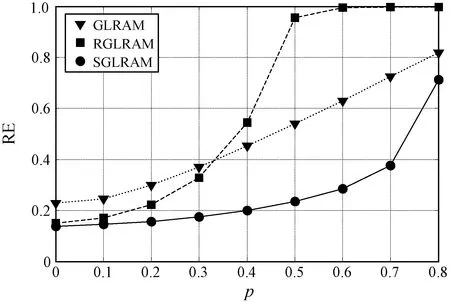
式中:L∈Rm×r1和R∈Rn×r2均为正交变换矩阵;Mi∈Rr1×r2;噪声矩阵Ei∈Rm×n;r1和r2满足max(r1,r2) 假设噪声矩阵Ei的元素服从独立同分布的均值为0的高斯分布,根据极大似然估计法可得GLRAM的最小化模型: (2) s.t.LTL=Ir1RTR=Ir2 (3) s.t.LTL=Ir1RTR=Ir2 一般而言,上述优化问题没有闭形式解,可通过奇异值分解来交替求解L和R[7]。 GLRAM模型适用于高斯噪声情形,但不能很好地处理大的稀疏噪声。文献[14]提出了鲁棒广义低秩矩阵逼近(RGLRAM)模型。为了增强模型对稀疏噪声的鲁棒性,假设式(1)中Ei的元素服从独立同分布的均值为0的拉普拉斯分布。基于极大似然估计法,可建立以下l1范数最小化问题: (4) s.t.LTL=Ir1RTR=Ir2 (5) s.t.Di=LMiRT+Eii=1,2,…,N LTL=Ir1RTR=Ir2 基于稠密高斯噪声与稀疏噪声叠加这一假设,建立了稳定广义低秩矩阵逼近算法(SGLRAM)。 假设数据矩阵Di同时受到大的稀疏噪声和高斯噪声腐蚀,则可将它分解为如下三项之和: Di=LMiRT+Ei+Gii=1,2,…,N (6) 式中:Ei是稀疏噪声矩阵;Gi是高斯噪声矩阵。进一步考虑矩阵Di均存在数据缺失,缺失元素对应的二维指标集记为Ωi,即当且仅当(k,l)∈Ωi时,Di的第k行第l列元素未缺失。为描述方便起见,将Di的缺失元素补充为0,新得到的矩阵记为Zi。对于Ωi,引入正交投影算子ΡΩi(·):Rm×n→Rm×n,其定义为PΩi(Di)=Zi。建立如下的SGLRAM模型: (7) s.t.Di=LMiRT+Ei+Gi PΩi(Di)=Zii=1,2,…,N LTL=Ir1RTR=Ir2 (8) s.t.Xi=LMiRT+Ei+Gi Di=XiPΩi(Di)=Zii=1,2,…,N LTL=Ir1RTR=Ir2 上述最小化问题等价于: (9) s.t.Xi=LMiRT+Ei+Gi Di=XiPΩi(Di)=Zii=1,2,…,N LTL=Ir1RTR=Ir2 式中:μ>0。在不考虑ΡΩi(Di)=Zi和正交约束情形下,构造式(9)的拉格朗日函数: (10) 式(9)是非凸的,因此无法直接使用现有的压缩感知方法求解。下面给出求解此优化问题的ADMM方法,即采用交替更新策略,每次只更新一个块变量。 (1)更新L。当L未知且其他变量固定时,L的计算过程如下: (11) (12) (13) 式中:QR(·)是矩阵的QR分解。容易证明:当更新完L和M后,fμ(L,R,M,D,E,G,X)值不会增加。 (2)更新M。当M未知且其他变量不变时,M的计算过程如下: (14) R:=QR(T) (15) (4)更新E。当E未知且其他变量不变时,E的计算过程如下: (16) 式中:Sσ(·):Rm×n→Rm×n为绝对值阈值算子[18]。 (5)计算G。根据以下公式更新G: 〈Y1,Xi-LMiRT-Ei-Gi〉= (17) 因此,fμ关于Gi偏导数为: 记Om×n为m×n维零矩阵,令▽Gifμ=Om×n,得到Gi的更新公式: (18) (6)计算X。当X未知且其他变量不变时,X的计算过程如下: (19) (20) (7)计算D。当D未知且其他变量不变时,D的计算过程如下: (21) 考虑到约束ΡΩi(Di)=Zi,进一步得到Di的迭代公式为: (22) (23) (9)计算μ。根据以下公式更新μ: μ:=min{ρμ,μmax} (24) 式中:ρ>1为一个常数;μmax是μ的最大取值。 算法1列出求解SGLRAM的ADMM算法的整个过程。 算法1求解SGLRAM的ADMM算法 输出:L、M、R、E、G、X和D。 初始化:L,R,Mi=LTZiR,Xi=Di=Zi, 迭代步骤如下,直至收敛。 1.根据式(13)更新L。 2.根据式(14)更新Mi,i=1,2,…,N。 3.根据式(15)更新R。 4.根据式(14)更新Mi,i=1,2,…,N。 5.根据式(16)更新Ei,i=1,2,…,N。 6.根据式(18)更新Gi,i=1,2,…,N。 7.根据式(20)更新Xi,i=1,2,…,N。 8.根据式(22)更新Di,i=1,2,…,N。 10.根据式(24)更新μ。 11.如果终止条件满足,终止算法;否则,转第1步。 在算法1中,可按如下方式随机初始矩阵L和R:L=orth(randn(m,r1)),R=orth(randn(n,r2)),其中randn(m,r1)表示按标准正态分布随机生成的m×r1维矩阵,orth(·)是按列标准正交化算子。算法1的收敛条件可以设置为: (25) 或者达到最大迭代次数,其中ε是一个足够小的正数。在后面的实验中,取ρ=1.1,μmax=1010,ε=10-9。 在人工合成数据集和ORL人脸数据集上进行实验,并将SGLRAM的实验结果与GLRAM、RGLRAM的结果进行比较。采用MATLAB R2012a进行编程,所有实验在处理器为Intel(R)Core(TM)i5-7400 @3 GHz的个人计算机上运行。 根据以下公式人工合成N个数据矩阵: Di=Ai+Ei+Gii=1,2,…,N (26) 式中:Di∈Rm×n;Ai是低秩矩阵;Ei是稀疏噪声矩阵,Gi是高斯噪声矩阵。具体地,Ai按如下方式产生: Ai=orth(U)Si(orth(V))T (27) (28) 相对误差越小,恢复性能越好。用两个逆信噪比(Inverse Signal-to-Noise Ratio,ISNR)分别来度量稀疏噪声和高斯噪声的噪声大小,其定义如下: (29) 设计两组实验来比较算法的性能,部分参数设置如下:m=n=100,N=50,r1=r2=20,λ=0.2,q=0.1,最大迭代次数为300。将实验重复10次,最终报告平均结果。 在第一组实验中,不考虑数据缺失情形。取a∈{0.5,1,2},σ∈{0.05,0.10}。a与σ不同组合取值下的实验结果如表1所示。可以看出:当σ固定时,a的取值对SGLRAM和RGLRAM的影响较小,这说明这两种方法对稀疏噪声更加鲁棒;SGLRAM具有最好的低秩恢复性能,其相对误差比RGLRAM的结果小0.004 9~0.015 1;当a固定时,σ的取值越大,SGLRAM的恢复性能越差,这说明高斯噪声水平对SGLRAM的恢复性能具有重要的影响;SGLRAM的运行时间最长,大约是GLRAM的5倍,是RGLRAM的1.8倍。总之,尽管SGLRAM的运行时间较长,但它在移除稀疏噪声与高斯噪声方面优于GLRAM和RGLRAM。 表1 (a,σ)不同取值的实验结果 (a)σ=0.05 选取英国剑桥大学Olivetti研究所的ORL人脸数据集作为实验数据。该数据集包含40个不同年龄、不同性别的人,在不同时间共获取400幅灰度图像,其中每个人有10幅不同的图像,且拍摄倾斜角度和旋转角度最大可达20°。这些图像展示了不同的表情和面部细节,每幅图像均被标准化为64×64的分辨率。对于第i幅图像,对其添加密度为0.1的椒盐噪声,记对应的含噪矩阵为Di,i=1,2,…,400。根据Di的近似低秩性来移除噪声。 对于SGLRAM,其他参数设置如下:r1=r2=20,λ=1,最大迭代次数为300。图2给出了GLRAM、RGLRAM、SGLRAM三种模型的部分图像的恢复结果。可以看出:GLRAM对稀疏的椒盐噪声比较敏感,而RGLRAM和SGLRAM却较好地移除了大的稀疏噪声。 (a)原始图像 (b)噪声图像 (c)GLRAM (d)RGLRAM (e)SGLRAM 对于受椒盐噪声腐蚀的人脸图像,下面考虑三种模型在不同缺失概率p下的恢复结果。令p∈{0.1,0.3,0.5,0.7},图3比较了某幅图像的恢复结果。观察图3,可以发现GLRAM具有最差的恢复性能,即使在p=0.1时,它都不能较好地恢复低秩图像。当p=0.1时,RGLRAM和SGLRAM均得到了较好的恢复结果,此时RGLRAM将缺失元素当作稀疏噪声,具有一定的鲁棒性。当p≥0.3时,RGLRAM具有较差的恢复性能,而SGLRAM具有较好的恢复性能。综上,SGLRAM不但对稀疏噪声具有鲁棒性,而且对缺失元素还具有一定的稳定性。 本文提出了GLRAM的一种稳定模型——SGLRAM。该模型假设低秩数据矩阵同时受到稀疏噪声和高斯噪声的腐蚀,并考虑数据存在缺失情形。建立了最小化矩阵l1范数与Frobenious范数的优化问题,并基于ADMM方法设计了迭代算法。实验结果表明本文方法不但对稀疏噪声鲁棒,而且对缺失数据具有稳定性。SGLRAM的全变差等正则化模型将是今后值得研究的一个方向。
1.2 鲁棒广义低秩矩阵逼近

2 稳定广义低秩矩阵逼近
2.1 SGLRAM模型建立
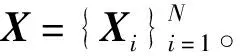
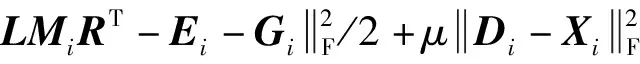
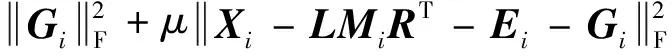
2.2 SGLRAM模型求解

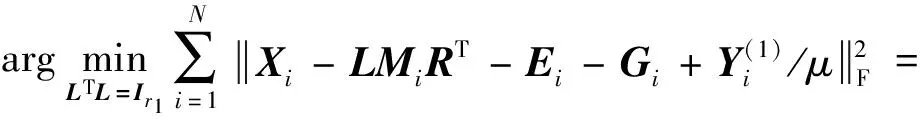
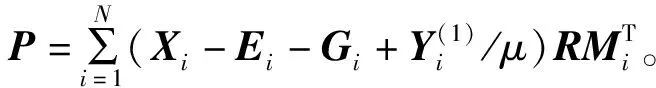
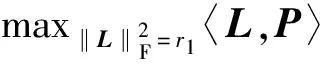
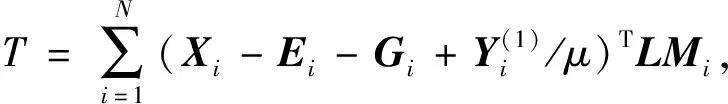

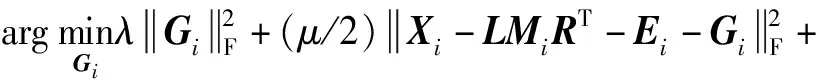


3 数值实验与结果分析
3.1 合成数据集实验
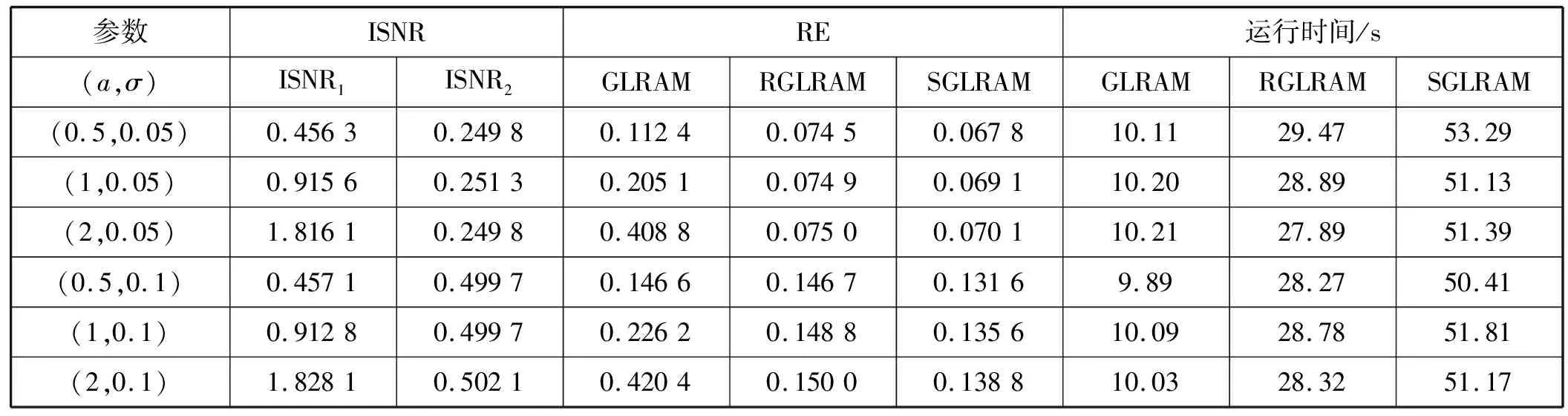

3.2 ORL人脸数据集实验

4 结 语

