基于多目标演化算法和改进概率分类的重尾时间序列预测

邹小云 林文学

1(湖北职业技术学院科研处 湖北 孝感 432000)2(湖北职业技术学院继续教育学院 湖北 孝感 432000)

0 引 言

随着互联网和计算机领域的普及和广泛应用，许多应用领域不断地产生新的数据流，如金融市场[1]、视频直播、语音通话和安全监控系统[2]等。数据流有别于传统的静态数据，所以传统数据挖掘技术无法直接用来分析数据流。数据流分析逐渐成为了数据挖掘领域的研究热点，频繁模式挖掘[3]、高效用模式挖掘[4]、概念漂移数据分类[5]、数据流异常检测是其中的重点方向。数据流分类方法要求时间序列的主要特征都出现后才能分类，但在天气预报、金融市场行情、网络安全等应用场景中，如果能尽早预测出数据流的趋势，能够为决策者带来巨大的效益。

为了在获得部分特征的情况下对整个时间序列进行提前预测，Alonso等[6]首次提出了时间序列早期分类的概念，利用基于谓词的分类器结合boosting算法可以达到早期分类的目的，但该方法的基分类器训练需要多次扫描样本。时间序列普通分类问题和早期分类问题之间的差别在于，前者的目标是最大化预测准确率，而后者存在预测准确率和早期性(时间提前量)两个冲突的目标。时间序列早期分类算法[7-8]主要分为两个类型：基于Shapelet的分类算法通过搜索时间序列中的Shapelet特征来判断样本的分类[9-10]；集成多个分类器评估不同时间戳的预测可靠性，确定预测分类的有效性。

在时间序列早期分类的问题中，早期性和分类准确率是两个冲突的目标，目前的主要方法是将这两个目标组合为一个总目标，再通过群体智能技术计算总目标的Pareto最优解[11]。如果使用30%的序列可获得80%的准确率，或者使用50%的序列可获得90%的准确率，难以判断这两种情况的优劣。在不同的应用场景下，对早期性和准确率两个目标的要求不同，如安全领域需要尽早检测出危险，而天气预报需要在指定天数前尽可能准确地预测出天气。现有的方法一般通过设置体现偏好的目标重要性参数来调节分类模型，但这种方法需要获取后验信息，并通过多次运行分类程序才能完成对参数的调节，显然无法适用于实时数据流预测的情况。

针对上述问题，本文将早期性和分类准确率作为两个独立的目标，采用演化算法同时优化两个目标，给出不同时间戳的预测准确率和早期性结果，供用户根据应用场景自行选择。此外，针对时间序列的重尾分布特点，对高斯过程分类进行了修改，提高对重尾分布时间序列的分类准确率。

1 时间序列预测算法设计

1.1 问题模型

首先给出时间序列预测问题的相关定义。

定义1一个长度为L的时间序列定义为：

TS={(ti,xi)|i=1,2,…,L}

(1)

定义2从时间t截断的时间序列定义为TSt，记为TSt={(ti,xi)|i=1,2,…,t}。

基于定义1和定义2，给出时间序列预测问题的定义。

定义3假设一个标记时间序列的训练集为X={(TS1,CL1),(TS2,CL2),…,(TSn,CLn)}，其中：TSi为时间序列；CLi为对应的类标签。时间序列预测分类问题定义为：根据一部分时间序列TSt*建立从时间序列到类标签的映射，并能够尽早预测出新到达样本的类标签。

1.2 时间序列早期分类的优化方法设计

本文的目标是获得一个集合{((h1,h2,…,hL),sγ1),((h1,h2,…,hL),sγ2),…,((h1,h2,…,hL),sγg)}，其中：{h1,h2,…,hL}为分类器序列；sγi为分类器对应的触发函数；{sγ1,sγ2,…,sγg}为优化的触发函数集。

本文方法主要分为3个步骤：训练概率分类器集，选择指定的触发函数，优化选择的触发函数集。

1.3 训练分类器

首先训练一个分类器集，负责预测每个时间戳样本的类标签，图1是训练分类器的主要流程。在训练时间戳t的分类器之前，提取X的所有时间序列，然后在时间戳t截断序列。时间戳t可以是绝对时间，也可以是序列长度的百分比。接着选择一个度量指标评估时间序列之间的距离，再组成一个距离矩阵。

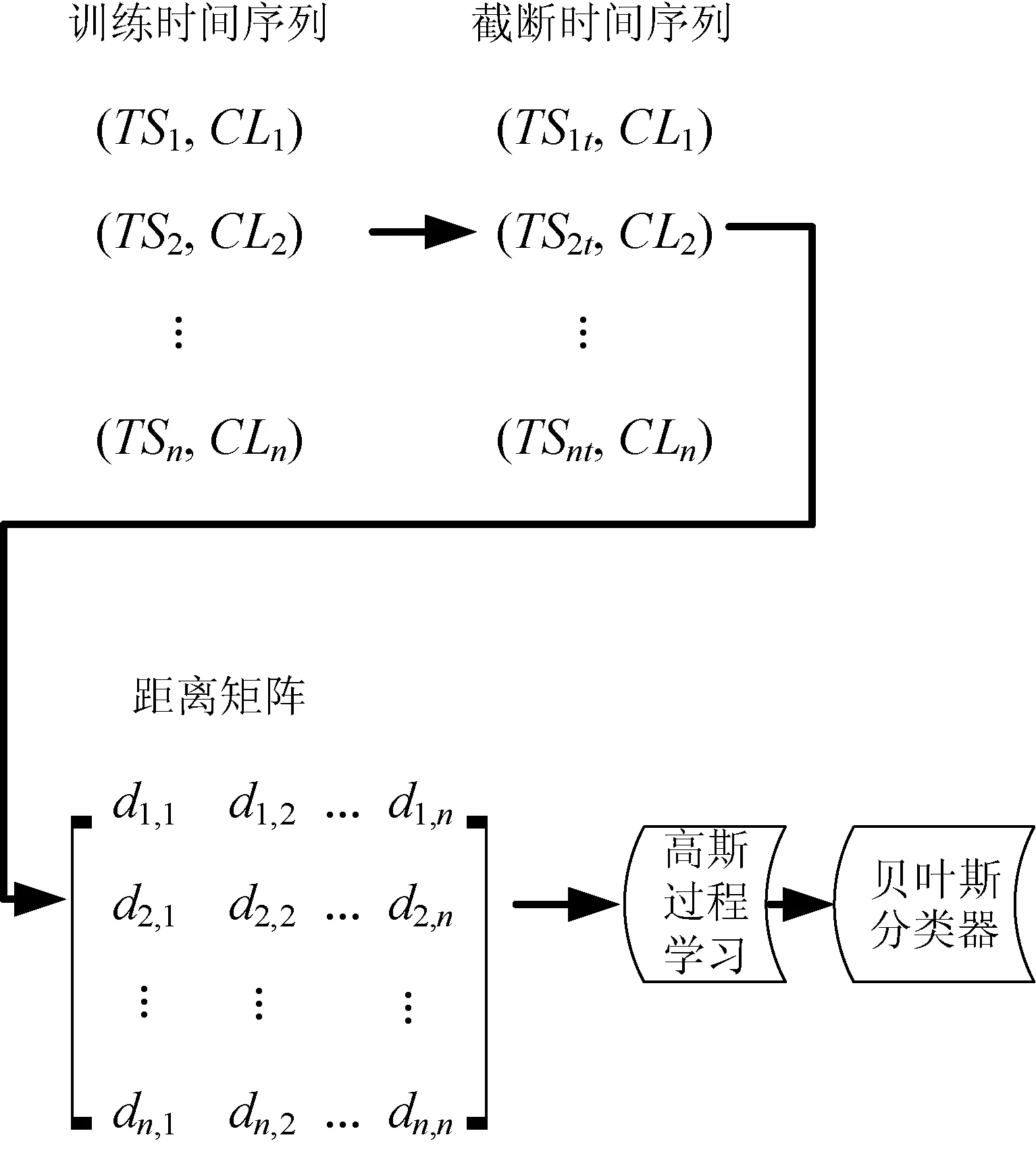
图1 分类器训练程序的流程

不同的学习算法对输入数据的格式具有特定要求，动态时间归整(Dynamic Time Warping, DTW)采用动态规划方法来进行时间规整的计算，尤其适用于不同长度、不同节奏的时间序列，所以本文采用DTW度量时间序列之间的距离。采用改进的贝叶斯分类器输出时间戳t的样本关于每个类的隶属度。

1.4 定义触发函数

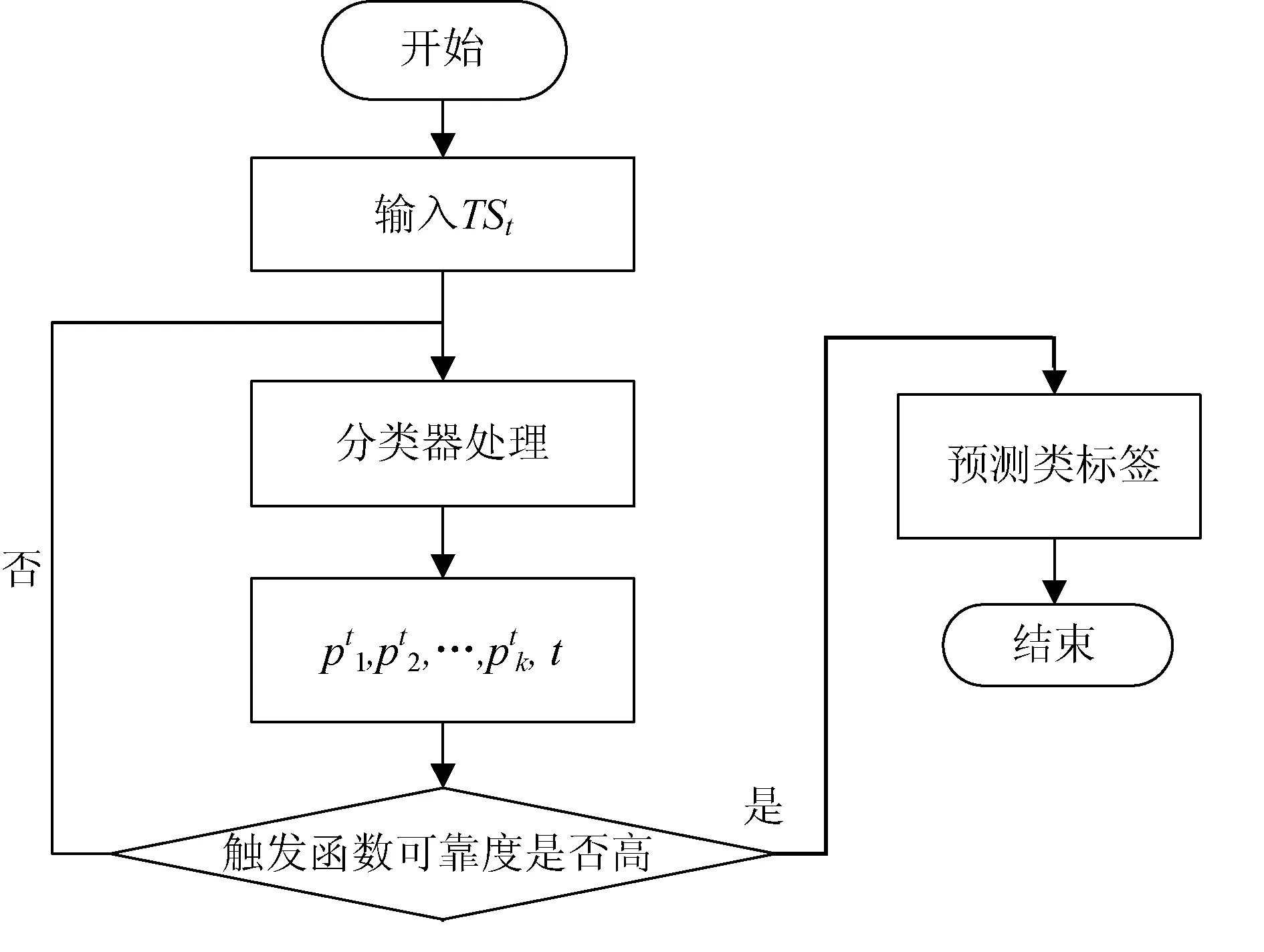
图2 时间序列预测分类的流程图

图2中触发函数的输出为0或者1。如果触发函数判断预测结果的可靠度高，则选择当前预测准确率最高的分类方案；如果触发函数判断预测结果不可靠，那么等待、收集更多的时间序列。线性触发函数定义为：

(2)

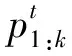
触发函数集内所有函数的形状均相同，区别在于γ参数不同，因此需要计算优化预测准确率和预测提前量的γ参数。

1.5 最优触发函数集

γ参数向量是决定触发函数(式(2))的关键，如果γi设为[-1,1]内的随机数，则可能出现重复值，并且其触发函数获得的预测准确率和早期性并非最优值。

1)评价触发函数的质量。为了评价触发函数的预测准确率和早期性，采用两个被广泛使用的评价指标，评估早期性质量的方法为：

(3)

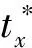
(4)

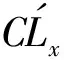
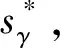
(5)

然后使用元启发式算法求解多目标优化问题。采用多目标优化的理由主要有三点：(1)如果将两个目标组合成一个优化问题，那么Ca和Ce必须缩放到相同的区间，才能使两个目标间保持平衡。(2)两个目标组合优化问题需要预先分配权重，该参数难以确定。(3)为了权衡两个目标的关系，需要多次运行程序，而多目标优化程序通过一次运行即可获得一组非支配解集。本文将非支配解集输出供用户根据具体的应用场景选择。

1.6 结构设计

本文目标是为用户提供一组分类器和触发函数的集合{((h1,h2,…,hL),sγ1),((h1,h2,…,hL),sγ2),…,((h1,h2,…,hL),sγg)}。图3是本文时间序列预测方法的结构，用户根据实际需求选择满足其预测准确率和早期性的最佳触发函数sγ*，本文算法基于触发函数sγ*和分类器(h1,h2,…,hL)来预测新时间序列的分类。

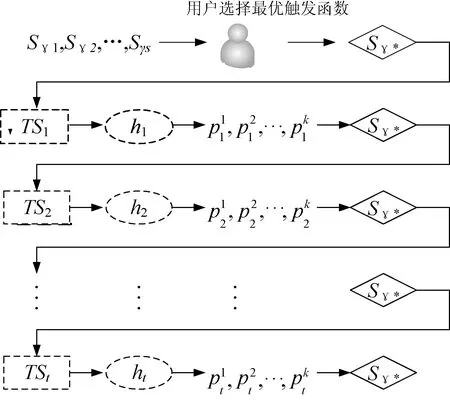
图3 时间序列预测方法的结构

2 概率分类器设计

设计开发了高斯过程分类器预测时间序列的分类概率，并针对重尾分布型时间序列进行了改进。将贝叶斯分类器和半参数模型结合，能够自适应调节模型的参数，并提高对时间序列中风险数据的预测能力。

2.1 时间序列的贝叶斯分类器模型

设yi(s)表示子集Si的训练函数，设ci∈{1,2,…,G}为对应的类标签。假设类g的观察样本满足相同的平均函数ηg(s)和协方差函数γg(s,t)，观察样本可以是动态或静态的。设πg表示观察样本属于类g的先验概率，分类器的目标是学习一个预测模型，将新观察样本y分配到G中的一个类。贝叶斯分类器的最优规则是最大化类g的后验概率：

(6)

式中：p(y|g)表示样本y的类标签为g的似然概率。

以网格形式记录序列函数曲线，设yit=y(sit)表示位置sit(t=1,2,…,ni)、第i个样本的观察函数。新的观察样本表示为向量形式y，将式(6)的p(y|g)替换为f(y|g)，其中f(·|g)表示类g的分布密度。式(6)的分类隶属度后验信息提供了分类不确定性的重要信息，该信息对于风险预测具有巨大的价值。传统的高斯过程分类生成每个曲线的极限后验概率，对于错误分类表现出过度置信，导致对重尾分布存在过度置信的问题。为了解决这个问题，本文对高斯过程分类做出修改，简称为改进的高斯过程分类器(Improved Gaussian Classifier,IGC)，IGC不仅降低了重尾分布数据的分类错误率，同时所估计的后验概率分布能够准确地反映样本在类中的不确定性。

采用分类错误率和对数损失LogLoss从不同角度评价分类器的性能，LogLoss通过惩罚错误分类实现对分类器准确性的量化。LogLoss定义为：

(7)

式中：i表示观察样本，如果i属于类g，那么Iig等于1，否则等于0；pig表示第i个观察样本分配到类g的预测概率。

2.2 改进的高斯过程

为了提高式(6)的鲁棒性和后验密度，将式(6)修改为半参数的混合高斯训练模型，定义为：

(8)

式中：i=1,2,…,Mg，Mg为类g的观察样本数量；yi表示第i个观察样本的离散响应(长度为ni)；Bi和Ri分别为ni×p和ni×q的样条基矩阵；β和γi分别为Bi和Ri的系数因子；εi为高斯模型的位移因子；tq和tni分别表示范围为q和ni的高斯分布；采用多变量的t-分布建模随机系数和度量误差，两者的自由度均设为v；Γ和Λi分别表示两者的缩放矩阵。

本文的改进模型保留了高斯模型原有的优点，如支持无参数的拟合平均函数，支持通过无结构的协方差矩阵Γ来近似曲线内的协方差结构，支持多种数据分布类型。高斯模型也具有一定的鲁棒性，对重尾分布也具有一定的处理能力，这也是本文选择以高斯分类器为基础的原因。

对每个类训练一个鲁棒模型，计算新观察样本对类的似然来近似式(6)。使用伽玛-正态混合分布表示多变量t模型，yi的边缘分布属于多变量的t-分布，定义为：

(9)

式中：vd为密度函数；设γi|τi～Nq(0,Γ/τi)和εi|γi两者之间条件独立，新到达样本概率τi服从正态分布：τi～Nni(0,Λi/τi)，也服从伽玛分布：τi～Gamma(v/2,v/2)。

参考文献[12]的方法将数据投影到一个特征函数的序列来近似式(6)的密度概率，采用基样条曲线来拟合离散的度量指数，本文方法能够处理不规则采样的数据和多曲线的分类问题。时间序列中存在许多高维数据的情况，因此分类器可能使用高维信息来建模密度，一般通过粗糙惩罚(L1泛化)或者稀疏性条件(L2泛化)来解决高维问题。因为本文的分类器在实数数据流的情况下工作，分类效率是一个关键的要素，所以本文采用B样条基进行无参数建模，从而使本文方法的计算效率高于L1泛化和L2泛化高维近似方法。

2.3 改进的高斯过程分类

在时间序列的实际应用中，存在大量重复的观察样本，所以观察样本之间存在相关性，通过分析相关的观察样本，能够加快时间序列预测的速度。为了考虑观察样本间的依赖性，对式(8)进行修改，增加类级别的随机函数，其系数服从以v为密度函数的t-分布。设yij为第i个类、第j次重复的nij维响应向量，如果每个类包含多次重复，那么将多级分类模型重写为：

(10)

式中：Dij为nij×r的样条基矩阵；δi为一个随机向量。根据多变量t-分布将每个样本分类；ψ表示高斯分布的偏差。

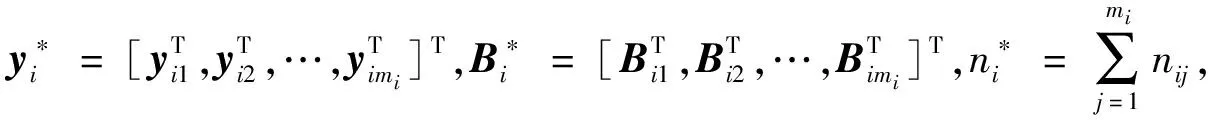
(11)

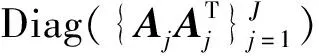
(12)

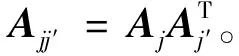
3 实 验

3.1 实验数据集

目前主流的时间序列早期分类算法和预测算法均采用UCR时间序列数据库作为benchmark数据库。本文从UCR数据库中选择17个不同应用场景的数据集，便于与其他算法的结果作比较。这17个数据集的应用场景不同、维度不同且分类数量也不同。将分类器的学习步长定义为时间序列总长度的5%，采用DTW度量时间序列之间的距离。

3.2 参数设置

本文方法包含两个重要的模块：双目标优化算法和分类器的学习算法。分类器采用本文所设计的改进高斯过程分类器。此外，需要通过双目标优化方法计算非支配解集，多目标优化方法并非本文的研究重点，因此选择3个被广泛应用的多目标演化优化算法分别与本文方法集成，评估本文时间序列预测方法的性能。3个双目标优化算法分别为非支配排序遗传算法(NSGA-II)、多目标萤火虫算法(MOFA)和多目标粒子群优化(MOPSO)。3个优化算法与本文方法的结合版本分别简称为NSGA_IPA、MOFA_IPA和MOPSO_IPA。表1所示是3个优化算法的参数设置。

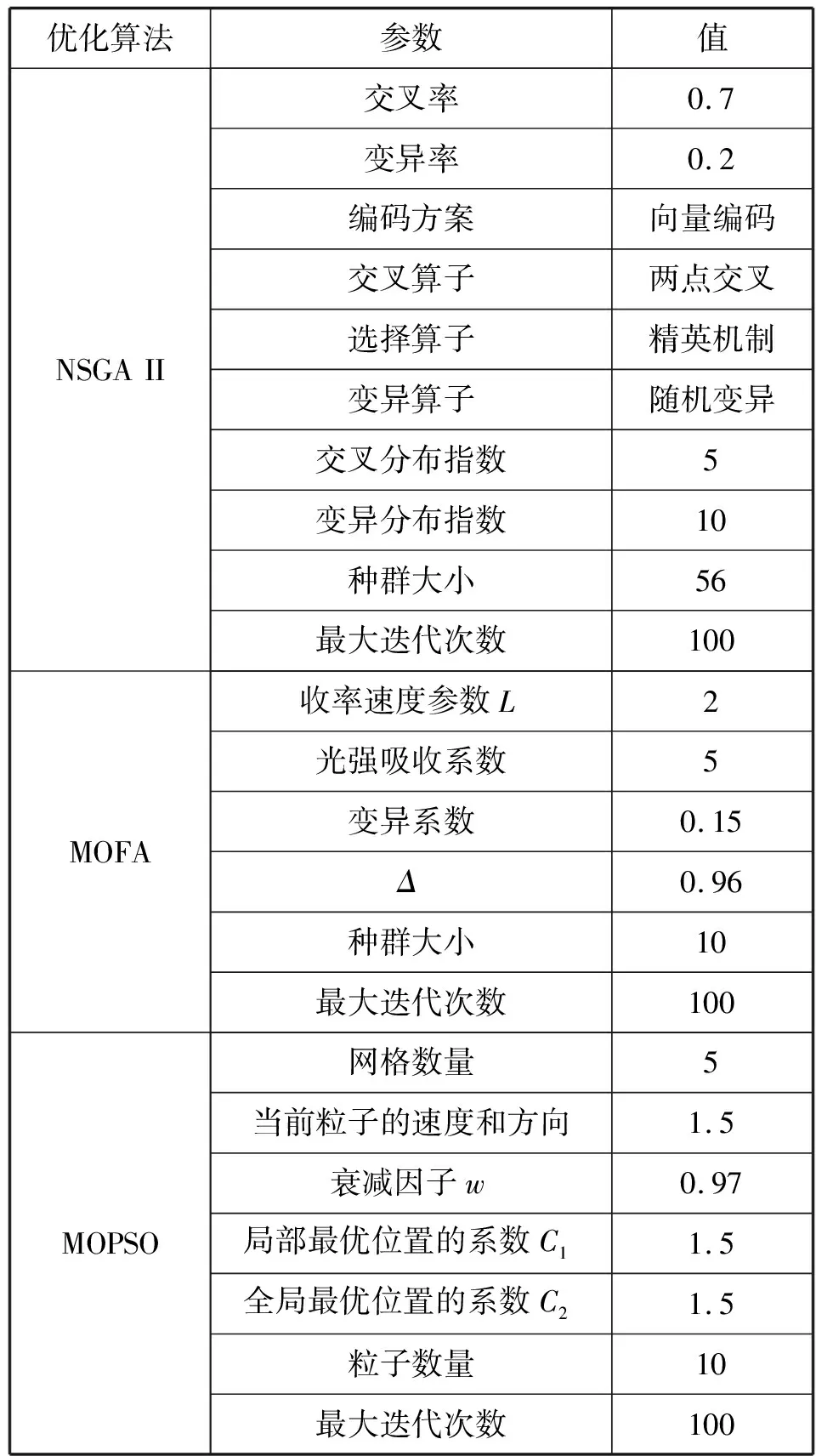
表1 优化算法的参数设置

3.3 对比方法选择

本文方法的特殊之处是独立优化预测准确率和早期性两个目标，而其他许多方法均将多个目标组合为一个单目标的优化算法。

本文方法与最近相关的2个时间序列早期分类方法做比较：CAEC算法[13]、ESC算法[14]。CAEC算法是一种广义的时间序列预测分类算法，该算法也是一种基于概率的分类程序，而本文方法也是基于概率的分类程序。ESC算法是一种基于Shapelet的时间序列分类算法，该算法与本文方法属于不同的类型，但其分类准确率好于其他基于Shapelet的算法。表2是这2个算法在实验中的参数设置。

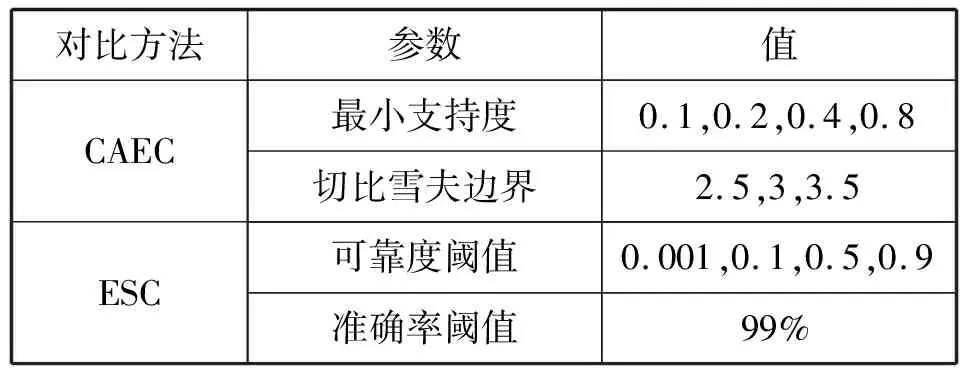
表2 对比方法的参数设置

3.4 实验结果分析

每隔5%的时间序列训练一组分类器，分别使用NSGA-II、MOFA和MOPSO算法作为优化算法，3个优化算法均采用随机的初始化种群。采用式(3)和式(4)分别计算早期性Ce和预测准确率Ca。

采用超体积指标[15]评估3个优化算法解空间的质量，该指标度量了解空间的体积。解集的超体积指标越大，表示其支配的解空间和覆盖的区域越大，其性能越好，该指标同时反映了解集的质量和多样性。统计了3个优化算法对17个数据集最小化Ca和Ce的超体积结果图，如图4所示，以(100,100)坐标为参考点，该坐标是最差的可能解。

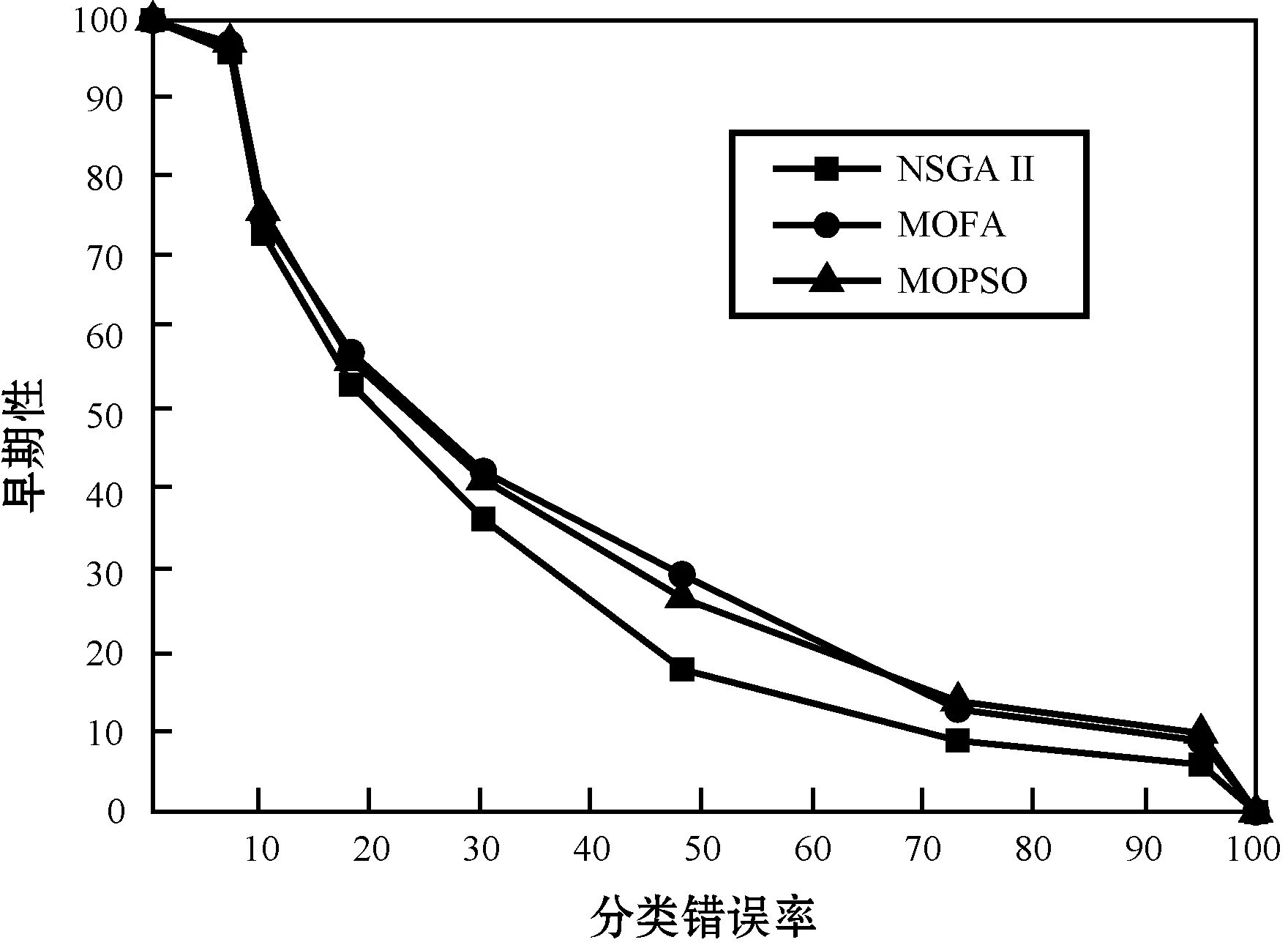
图4 3个优化算法最小化成本Ca和Ce的超体积结果比较

图4并未统计其他3个对比方法，因为它们的目标是以分类准确率为支配目标，在大多数情况下仅获得了极少的解。从图中可看出，本文方法和3个优化算法的组合方法均获得了较多的解集，其中NSGA_IPA的求解质量略好于其他MOFA和MOPSO，因此选择NSGA_IPA作为实验方法。

3.5 时间序列的预测实验

(1)搜索的解集。表3所示是3个预测方法对于17个数据集获得的解集数量统计，表中“i/j”中i表示非支配解的数量，j表示计算的所有解数量。可看出CAEC计算了固定的总候选解的数量为8，ESC也计算了固定的总候选解的数量为12，本文方法则提供了较多的候选解数量，并且从解集中提取出非支配解供用户选择。总体而言，本文计算的解集数量远高于其他2个算法。

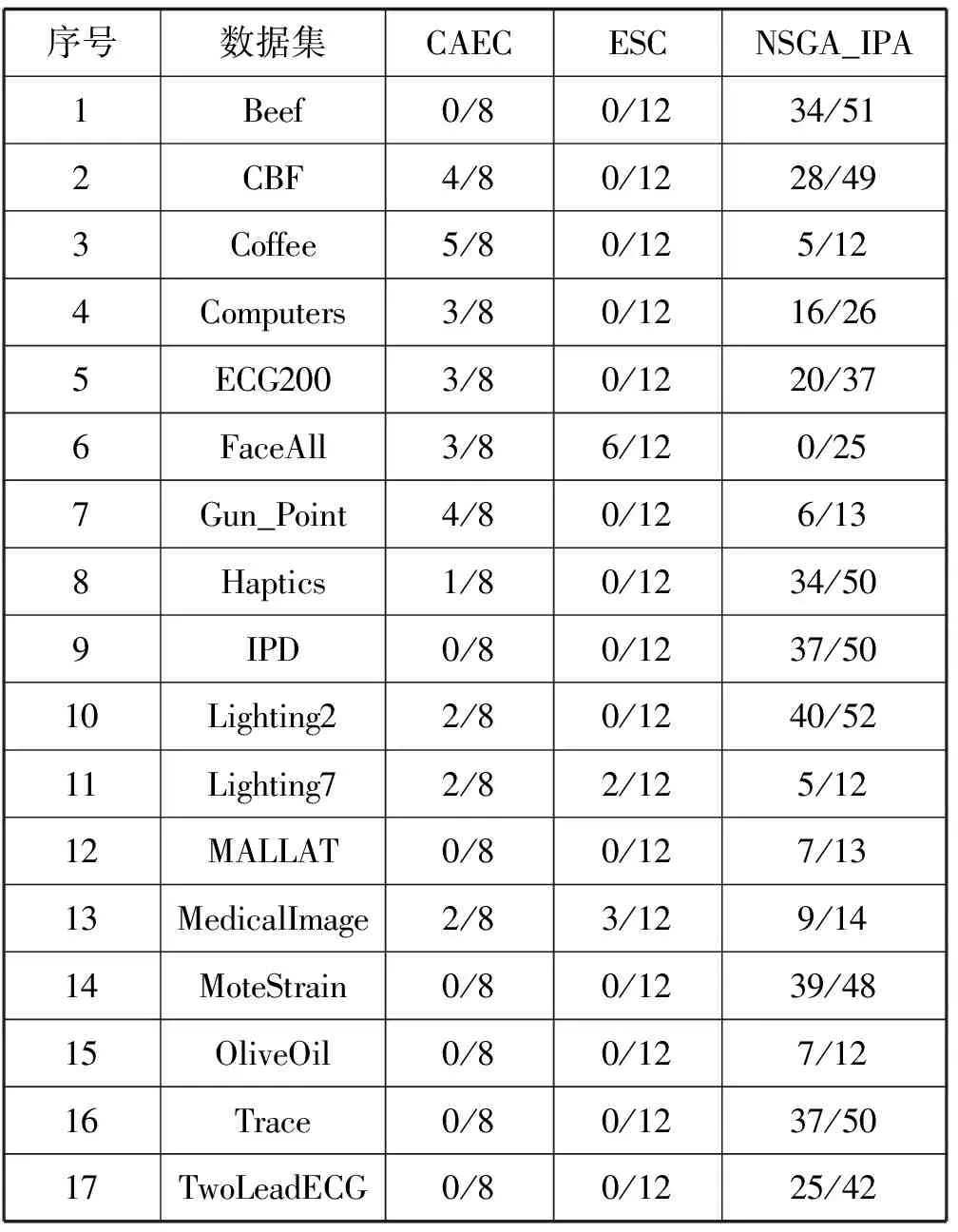
表3 3个预测算法的解集数量

(2)预测准确率的结果。虽然本文的目标是为用户提供非支配解集，使用户按照应用需求选择最合适的解，但本文方法对高斯过程分类进行了改进，有效地提高了重尾分布时间序列的分类性能。CAEC和ESC 2个算法均以最大化分类准确率为支配目标，以早期性为约束条件，所以这2个算法的分类准确率应当较为理想。此外将本文方法和普通高斯过程分类方法结合，组成的算法简称为NSGA_GC，比较本文对高斯过程分类的改进效果，NSGA_GC和NSGA_IPA的支配解作为该组实验的性能结果。4个时间序列早期分类算法对于17个数据集分别进行了预测分类实验，每组实验独立运行30次，统计30次的平均准确率作为实验结果，如图5所示。比较NSGA_GC和NSGA_IPA两个算法，NSGA_IPA对于17个数据集的分类准确率均高于NSGA_GC，反映出本文对于高斯过程分类的改进效果较好。ESC的预测准确率与本文算法较为接近，ESC通过检测Shapelet实现了较好的分类准确率。但综合17个数据集的结果，NSGA_IPA的预测分类质量最高，并且提供了丰富的解集供用户选择。

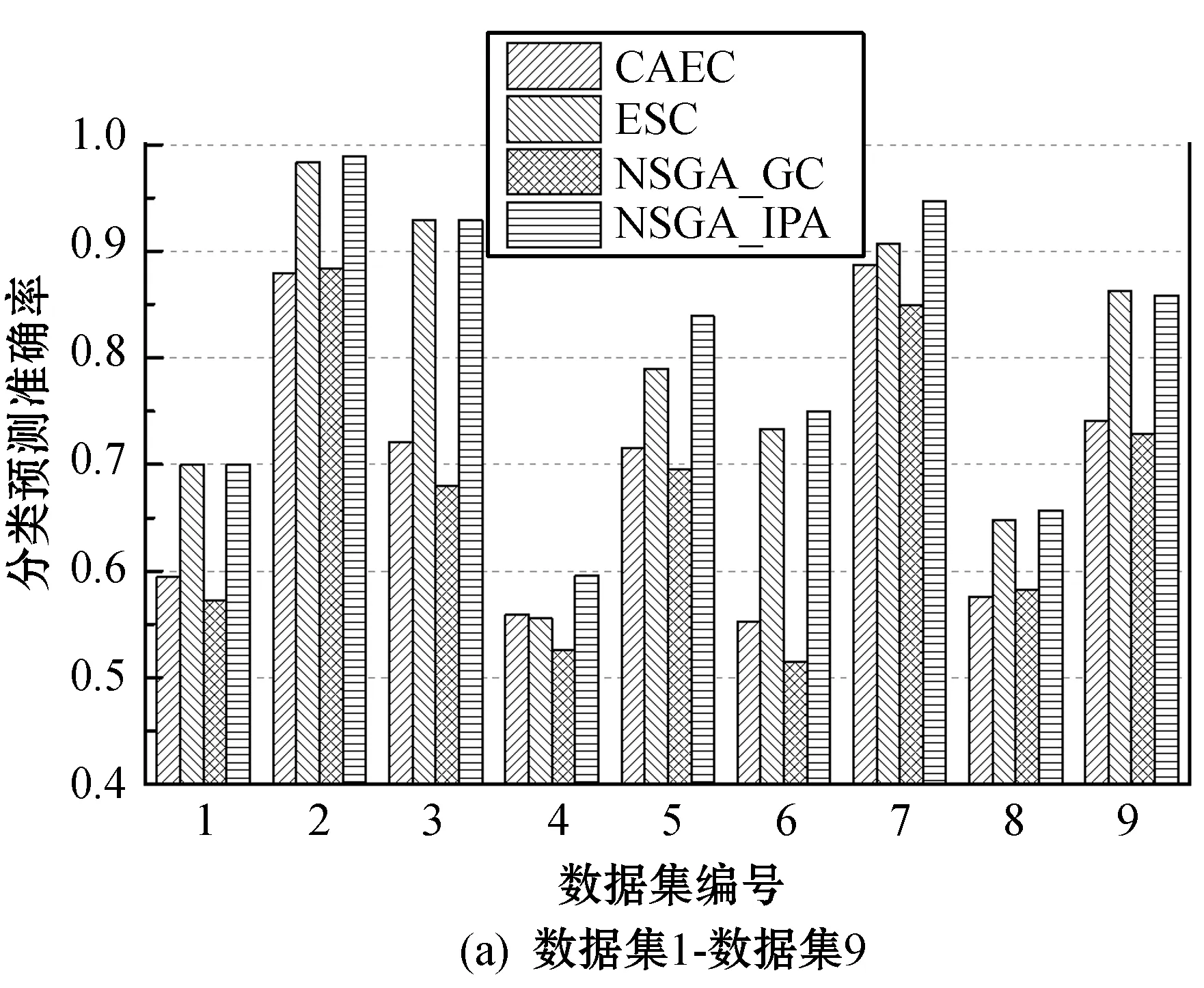
图5 时间序列早期分类的平均准确率

4 结 语

本文将早期性和分类准确率作为2个独立的目标，采用演化算法同时优化2个目标，给出不同时间戳的预测准确率和早期性结果，供用户根据应用场景自行选择。此外，针对时间序列的重尾分布特点，对高斯过程分类进行了修改，提高对重尾分布时间序列的分类准确率，并且优化了时间效率。实验结果表明，本文算法有效地提高了时间序列的预测准确率，并为用户提供了丰富的非支配解集。

本文采用了经典的3个多目标优化算法完成了仿真实验，优化算法是本文时间序列早期分类的一个关键部分。未来将针对早期性和预测准确率2个指标研究更加合适的多目标优化算法，以提高算法的总体性能。