利用机器学习和双平面博弈模型的车联网拥挤感知路由算法

谭晓芳 张 搴 付凡成

1(南昌理工学院计算机信息工程系 江西 南昌 330044)2(郑州轻工业大学计算机与通信工程学院 河南 郑州 450002)

0 引 言

车载自组织网络作为一种特殊类型的移动自组织网络(Mobile Ad-Hoc Network, MANET)，已成为智能交通系统(Intelligent Transportation System, ITS)的重要组成部分[1]。在VANET中，车辆配备有车载单元(On-Board Units, OBU)，这些单元能够用于事件数据记录器、全球定位系统、前向和后向雷达、传感设备和短程无线接口。使用OBU，每个车辆充当发送器、接收器和路由器，以将信息传递给其他车辆。此外，这些车辆还可以与沿路边部署的其他固定基础设施通信，这些基础设施被称为路侧单元[2](Road Side Units, RSU)。作为互联网接入点，RSU在蜂窝网络中扮演基站的角色。通常，VANET由RSU和车辆的OBU组成，它们在动态变化的VANET环境中反复交互[3]。

在VANET的运营期间，有两种基本技术可以传播车辆应用的数据：车辆与基础设施(Vehicle-to-Infrastructure，V2I)和车辆与车辆(Vehicle-to-Vehicle; V2V)之间的通信。V2I通信可以帮助车辆从/向RSU下载/上传内容，并且V2V通信主要依赖于车辆之间的协作来交换数据分组，而无需RSU帮助。V2I和V2V通信必须共存并相互补充，以满足VANET的各种通信要求[4]。为了确保VANET性能，通过V2I和V2V通信有效地传递信息对于为移动车辆提供满意的服务变得重要。大多数研究都考虑如何有效地管理涉及V2I和V2V通信的控制问题[5]。随着VANET的蓬勃发展，车载拥挤感知(Vehicular Crowd Sensing, VCS)成为一种新的范例，它利用普遍存在的传感器嵌入式OBU来有效地收集数据。文献[6]使用基于语义的信息网络新范式，解决了车联网中信息传播的问题，并对所提出模型的流量模型和网络架构进行了表征。文献[7]提出了两种新的路由算法用于群体传输车载网络，所提算法能够在较低开销下改善数据传输，而且开销可忽略不计。文献[8]从云计算和车辆互联网(Internet of Vehicles, IoV)之间的服务关系角度讨论了云辅助的分类，提出了一种利用来自联网车辆的数据来提高运输效率的新方法。文献[9]通过拥挤感知(Efficient Data Dissemination by Crowdsensing, EDDC)方案有效解决了数据传播问题，并在车载网络中提出了一种混合路由机制。

本文提出了用于VANET管理的新型V2I和V2V算法。对于V2I通信，基于激励的VCS算法开发了一种新型垂直博弈模型。在垂直博弈中，车辆和RSU是博弈玩家，车辆充当移动传感器以收集所需信息，RSU充当系统服务器以共享和处理多种类型的收集信息。对于V2V通信，开发了一种新的水平博弈模型，以实现基于学习的车辆间通信协议。在横向博弈中，车辆是博弈玩家，以提高路由服务的质量和可靠性。在动态变化的VANET环境下，本文方案被设计为双平面垂直—水平博弈模型。通过考虑现实世界的VANET环境，提出的算法交互式顺序博弈过程的方法是合适的，同时也确保了系统的实用性。为了研究每个博弈中博弈玩家之间的战略互动，采用强化学习方法。强化学习涉及系统代理如何采取行动以最大化其奖励。本文主要创新如下：

1)针对VANET设计了用于V2I和V2V通信的新型双平面模型，在纵向博弈模型中网络代理和车辆将向着拥挤感知过程工作；在横向博弈模型中VANET为车辆选择最佳路线。

2)基于横纵向模型，利用强化学习的自主学习和优化决策为车联网拥挤感知提供了一种有效的双平面控制机制，能有效提升RSU任务成功率。

3)不同于现有方案的非自适应性和离线模式，所提算法基于分布式在线方法实现拥挤感知的自适应性和实时性，并通过控制决策权衡最优性和适用性。

本文算法将动态VANET环境的响应以及博弈论和强化学习算法的相互组合，与现有方案相比，在RSU的任务成功率、规范化路由吞吐量和端到端数据包延迟方面有较大改善。

1 方案设计

本文方案主要由基于强化学习的VCS策略和基于双平面博弈模型的路由算法组成，其中双平面博弈模型和强化学习是VANET控制方案的理论基础。通过采用基于强化学习的博弈方法，并结合分布式在线计算和有效的路由算法，以适应快速变化的VANET环境。本文方案整体思路如图1所示。

图1 所提方案的整体架构

1.1 新型纵向和横向博弈模型

博弈玩家N={R,V}的有限集合，其中：R代表RSU，V={V1，V2,…，Vi,…,Vk}是多个车辆的集合，Vi是第i个车辆，k是GV2I博弈的车辆数量；车辆则被假定为VCS过程中的移动节点。

RSU中有限的传感任务集合X={X1，X2，…，XS}，S是总传感任务的数量。

(1)

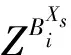
T={H1,H2，…,Ht,Ht+1,…}表示时间，其由具有用于V2I通信的不完全信息的一系列时间步骤表示。

GV2V可以制定用于路线操作的车辆的相互作用。

有限的一组博弈玩家V={V1，V2，…，Vn}NVi，其中n是GV2V博弈的车辆数量。

NVi是Vi的邻近车辆。

UVi∈V是Vi收到的回报。

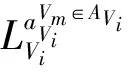
T={H1,H2，…,Ht,Ht+1,…}表示时间，其由具有用于V2V通信的不完全信息的一系列时间步骤表示。

1.2 利用强化学习的VCS策略

强化模型[12]能选择执行使系统状态得到更多增益的行为，这主要由该模型通过对系统现有状态的感知，并对下一步的行为所能带来的增益进行计算和评估来实现的；若节点执行状态的决策发生了变化，便可以得到执行此行为的系统增益值。由图2可知[13]，在路由发现过程t时刻，网络中的每个节点都会选择不同的动作策略ai(t)来共同对网络产生影响，节点从状态si(t)转换到si(t+1)后，便得到ri(t+1)即环境回馈的相应回报值，然后各个节点对自身的价值函数Vi(s)再次进行新的评估，并对邻居节点广播该函数。

图2 强化学习决策过程

对于单一节点的系统状态评估值，可以使用无限视野价值评估模型来对其进行计算：

(2)

并且将未来有限步内的系统状态转换所带来的增益rt设置为拥有同样的权重γ。对于系统的优化问题，可以将其转化为对由源节点S到目的节点D中经过的所有数据传输节点进行调整的决策过程，从而得到价值函数V(s)的最大值，以下为具体的求解过程。

将系统状态集记作S，当前状态能执行的动作集记作A，并且S和A的某种运算结果都可以使用系统增益R以及状态转移分布函数T(·)来表示。此处从状态s执行动作a带来的系统增益由R(s,a)表示，s经过动作a后转移到s′的概率由T(s,a,s′)表示。对贝尔曼方程进行求解可得系统最优解V*(s)：

(3)

式中：状态转移增益权重记作γ；在状态集S中所对应的每个状态s′的当前价值评估值记作V*(s′)；将价值评估函数V*(s)能得到最大值的动作记为a，并选择动作a作为下一步的状态转移操作。

将T(s,a,s′)作为每一条通信链路数据投递成功和投递失败的比例，并对所有节点对尝试发送的单播包数NA、单播传输失败包数NF、接收到的单播包数NR、接收到的广播包数NB和混杂接收单播包数NP等统计量进行记录，从而对T(s,a,s′)进行计算。对投递率进行计算时，需要在接收数据包统计量前面加上置信参数σ，并把ρ当作节点没有发送数据包时的投递率估计值，得到最终投递率表示为：

(4)

式(4)表示的是系统接下来的状态转换为投递成功s′=S时的转移概率T(s,a,S)。因为指定了rS和rF为固定值-1和-7，因此T(s,a,s′)的简单组合函数为：

R(s,a)=rS·T(s,a,S)+rF·T(s,a,F)

(5)

由此，T(s,a,s′)、R(s,a)评估模型得到了确定，再对贝尔曼方程进行求解可得V(s)的最优值：

(6)

通过分析可知，每个动作集a只会让当前状态s向两种可能的状态进行转换，若P表示为下一跳的节点，那么系统状态就会转变为两种可能：1)发生传输成功事件S，系统会从当前状态s=N转化到s′=P；2)发生传输失败事件F，系统当前状态s=N就会保持停留使得s′=N。由此可得系统Q值的计算过程为：

Q(N,P)=pS·[rS+V(P)]+pF·[rF+V(N)]

(7)

式中：数据包成功传输到节点P的概率由pS表示；传输失败的概率由pF表示。转化成求解问题：

(8)

若通过评估模型计算得到最优值函数，则选取能让每个状态能够获得最大Q值的动作就是最佳的决策过程，并将该过程称为系统的开发策略。

1.3 双平面博弈模型结合强化学习的V2V路由算法

V2V通信代表了支持使用端到端多跳路由的各种上下文感知应用程序的最理想技术之一。当日常道路旅行的安全性、效率和舒适性需要提高时，车辆间通信是实现这一目标的关键。然而，不同的车辆移动性经常导致不可靠的连接性和相应不稳定的服务质量。因此，MANET的传统路由协议表明它们在VANET中的性能很差；VANET的路由协议应该能够克服车辆的高移动性。

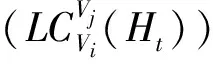
(9)

(10)

在路由路径形成期间，每个单独的车辆估计其相邻车辆的LC值。目标车辆一跳内的车辆的PC值设置为从它们自己到目的地节点的单跳LC值。其余车辆，即Vj，LC值设定如下：

(11)

基于邻近车辆的PC值，可以估计V2V通信的路由成本。通常，大多数V2V路由算法是通过依赖于车辆协作的假设来设计的，假设车辆愿意充当路由路径中的中继节点，而充当中继节点的车辆必须牺牲其能量和带宽。因此，路由算法需要刺激VANET车辆之间的合作行为才能有效[16-17]。

(12)

(13)

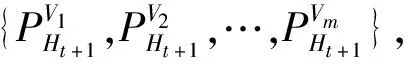
(14)

V2I和V2V算法的伪代码如算法1所示。

算法1V2I和V2V算法

函数V2I(){

1.初始化参数

2.使用式(1)，制定车辆选取策略Sv使收益uv最大化

3.使用式(2)，确定价值评估模型

4.使用式(3)和(4)，确定目标函数和投递概率

5.使用式(5)进行函数组合

6.Call V2V()

}

函数 V2V(){

1.使用式(6)，获得最优值

2.使用式(7), 获得系统Q值

3.使用式(8), 在源车处获得到达目的地车辆

4.使用式(9), 进行估计

5.使用式(10), 获得求和

Return

}

函数 Main(){

1.初始化控制参数。

2.学习值并平均分配。

For(; ;){

3. Call V2I()

}

}

1.4 算法流程

基于强化学习的垂直和水平博弈模型，通过逐步交互式博弈过程设计了一种新型V2I和V2V通信算法。该算法允许RSU和车辆学习当前的VANET情况并确定他们的最佳策略。在V2I博弈模型中，每个车辆通过参与VCS服务获得激励。在V2V博弈模型中，该激励被用作虚拟货币以补偿中继车辆的成本。在实际操作方面，可以将计算负担从中央系统转移到分布式车辆。所提出的V2I和V2V算法的流程如图3所示。

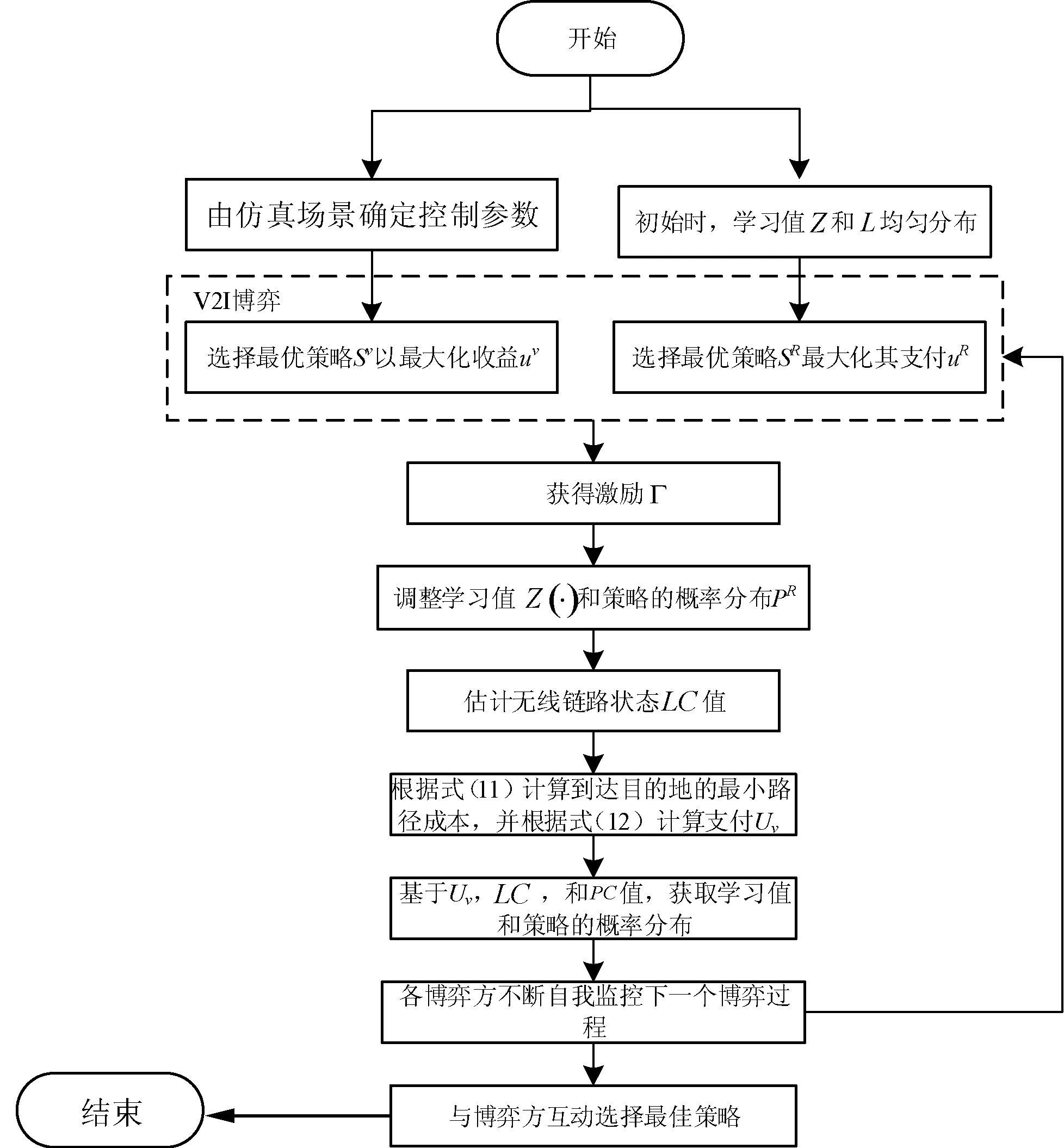
图3 本文算法流程图

2 实 验

基于MATLAB/2016b仿真环境搭建了用于VANET的仿真平台，该平台运行于Windows 8 GB RAM 64位 Inter(R)CoreTMi5-7500K 2.7 GHz台式计算机中。为验证本文方法的感知和路由性能，将其与文献[6]、文献[8]和文献[9]所提方法进行比较。文献[6]制定了一个移动众包博弈方案，其中每辆车根据传感和传输成本以及预期的支付选择其传感工作，而服务器根据其传感精度支付每辆车的成本。文献[8]中，车辆必须在数据更新之前检索所有数据单元，否则检索数据单元版本将不一致，车辆必须在规定的延迟要求范围内接收所有要求的数据单元，此外实验方案侧重于异构车辆网络中协同状态下同态数据的分发效率。文献[9]侧重于车联网数据中的带宽效率与业务异构性，实验方案中车流量负载设置略有不同。EDDC方案通过使用附近RSU的拥挤感知来设计混合路由，以保证车载网络中数据传播的质量。文献[9]评估了一种机会性拥挤感知方案，其中来自大量连接传感器的流量通过新兴的NB-IoT技术传输，基于仿真结果，确认了其优越性。为确保公平比较，根据文献[18]，针对本文方法的实验，采用以下假设和对应的实验方案：

• 假设模拟系统是VANET的常见无线通信系统。

• 在200 km路段上随机分布了1 200辆车和60辆RSU，每辆移动车的速度随机选择为40 km/h、80 km/h或100 km/h。

• 每辆车的最大无线覆盖范围设置为500 m。

• VCS的车辆成本C设置为RSU与相应车辆之间的相对距离与最大覆盖范围的比率。

• 随机选择源车辆和目的车辆。最初，每辆车的虚拟货币设定为100。

• 数据包在源节点以k(包/s)的速率生成，并且提供的负载范围在0～4.0之间变化。因此仿真模型中的持续时间H为1 s，模拟的总持续时间为2 h。

• 假设车辆不受噪音或物理障碍的影响。

• 车辆带宽容量为20 Mbit/s，每条消息由CBR数据包组成。

• RSU的任务和容量分别为10和2 Gbit/s。

• 基于200次模拟运行获得的网络性能测量被绘制为每秒数据包生成的函数。

为了证明方法的有效性，测量了RSU的任务成功率，标准化路由吞吐量和端到端数据包延迟。表1为仿真实验中所使用的系统参数。

表1 模拟实验中使用的系统参数

图4比较了每个方案的RSU任务成功率。任务成功率是以任务完成相对于总RSU任务的百分比来衡量的，是V2I通信操作中的关键因素。随着车辆的交通负荷增加，车辆致力于其自己的V2V通信，导致任务成功率降低。所有方案都表现出类似的趋势，然而本文方案在从低到大的交通负荷情况下优于现有方法。RSU在交互式垂直博弈过程中为车辆支付适应性激励，车辆自发地参与了众筹工作。这种情况可以保证比其他方案更高的RSU任务成功率。

图4 RSU的任务成功率

图5比较了路由吞吐量。路由吞吐量被定义为在目的地车辆处接收的数据分组与在源车辆中生成的数据分组的总数的比率。通过本文方案实现的路由吞吐量的增益，是采用迭代学习模型的有效水平博弈范例的结果。特别地，本文方案捕获相对距离和车辆的稳定性，自适应地选择从源车辆到目的地车辆的最佳路线路径。该方法可以增加V2V通信中的路由吞吐量。因此，本文方案实现了优于现有方案的路由吞吐量性能，现有方案被设计为单侧协议并且不响应当前的VANET条件。

图5 规范化路由吞吐量

图6曲线表示归一化的端到端分组延迟。通常随着分组生成速率增加，分组延迟随着业务负载线性增加。由于本文方案以分布式学习方式建立路由路径，因此在每个水平博弈时段，提出的V2V通信算法中的每个车辆通过反映VANET环境中的变化来自适应地做出路由决定。所以，本文方法比其他方案更有效地减少了分组延迟。

图6 规范化的端到端数据包延迟

仿真结果表明，本文方案使用基于学习的双平面博弈模型，可以监视当前的VANET条件并适应高度动态的环境。方法中的RSU和车辆从环境中获取信息，获得知识，并以自适应的方式做出明智的决策。仿真结果表明，该方案通常表现出比现有文献[6，8-9]方案更好的性能。尽管本文方案没有提供最佳解决方案，但比现有方案具有实质性优势。表1中的系统参数值是可变的，如果更改变系统参数值，则会更改模拟结果。在不同的模拟参数值下，性能趋势几乎相同。不同的仿真场景实验结果证实了本文方案优于其他现有方案。

3 结 语

在VANET中，针对V2I和V2V通信问题，本文提出了一种新型双平面博弈模型。基于VANET的特征，集成了交互式反馈机制，并基于强化学习和博弈论概念设计了纵向和横向博弈模型，开发了适用于不完备信息条件下的高效VCS和交互式路由算法。在所提出的双平面博弈模型中，单独的RSU和车辆是博弈玩家，并且为自适应的机会性VCS和路由动态地学习其策略。使用基于反馈的自我监控和分布式学习技术，博弈玩家可以动态地适应当前的VANET情况，并有效地最大化预期收益。通过仿真实验与现有方案进行对比，证明了本文算法在RSU任务成功率和吞吐量等指标的显著改善。

尽管本文算法已经实现了VANET管理中提高吞吐量和VCS任务完整性的目标，但仍有待进一步提高VANET系统效率。其主要问题包括在负载平衡、认知无线电和网络安全领域设计和验证新的VANET控制方案。此外，当RSU旨在最大限度地减少对车辆的总支付时，可以扩展包括博弈模型中简单惩罚的设计机制，以优化VANET特征控制算法。