一种基于单目视觉的智能机械臂系统
(天津科技大学,天津市河西区,300202) 文婉欣 张鑫 白 净
关键字 机器视觉;图像处理;标定
1 一种基于单目视觉的智能机械臂系统的工作原理
如果要让机器人完成抓取,需要通过视觉知道所抓物体的具体位置,本文中我们用相机来模拟机器人的视觉。在本系统中,相机固定安装,通过相机获取物体的图像,对物体的图像采集成功后,再对图像进行灰度图阈值处理、高通滤波、边缘提取等预处理;进行单目视觉定位,通过获得物体相对于相机的位置以及相机相对于机械臂的位置,以得到物体相对于机械臂的位姿,最终获得物体在图像中的位姿。为了保证位姿测量的准确性,就需要标定系统的内外参数,即进行相机标定和手眼标定:使其完成在世界坐标系、相机坐标系、图像坐标系、像素坐标系下的依次转换。之后再传送位姿,将工件在机械臂坐标系中的位姿传送至机械臂,利用c++编程引导机械臂完成工件抓取。
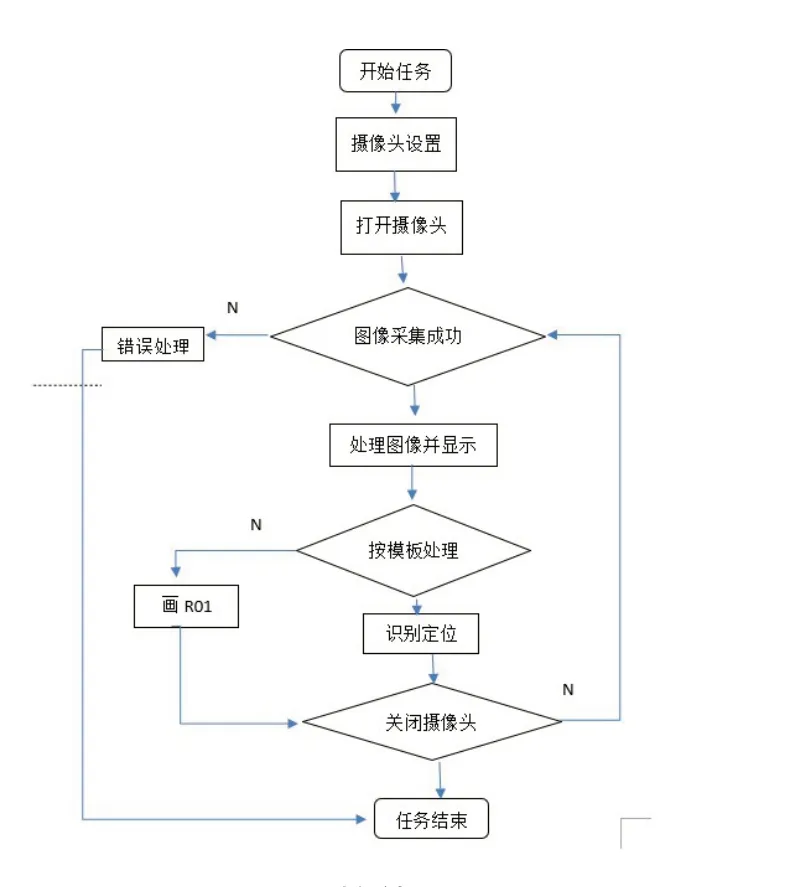
图1 整体流程图
2 相机标定
首先,标定相机的内外参数,内参数主要是相机的基础矩阵camera matrix=和畸变向量Distortion coefficients=(k1k2p1p2k3)。外参数主要是相机的旋转矩阵
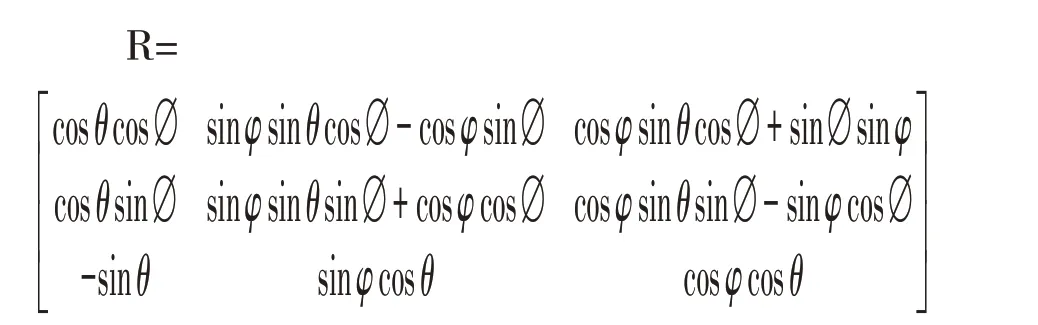
相机标定坐标系主要是通过计算机视觉技术来进行数据和参数的采集,然后再利用计算机技术将参数进行三维建模,从而使整个空间的三维坐标得到复原。首先需要相机从不同方位(至少两个)来观测标定板,加载好图像后设定参考位姿,创建一个投射图来描述图像平面与坐标轴系统中平面Z为零之间的映射。因为相机的成像原理是小孔成像,通过映射将三维显示世界转变为二维图像。二维点用m=[u,v]T,三维点用M=[X,Y,Z]T表示。x˜表示增广向量,最后一个元素加1:m˜=[u,v,1]T,Mˉ=[X,Y,1]T。三位点M和它图像投影点m关系如下:
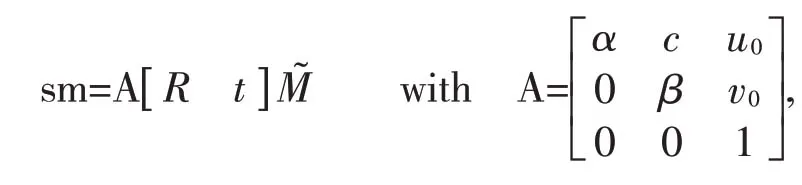
式中s是任意的比例因子。(R,t)称为外参,R是旋转矩阵,t是平移矩阵。A是相机内参矩阵,(u0,v0)是坐标的主点,α和β是图像在u和v轴的比例因子,c是描述两个坐标轴倾斜角的参数。一般情况下,假设模型平面在世界坐标系中的Z坐标为零,R的第i列旋转矩阵为r,从公式可知,当Z=0 时,M 可以表示为M=同样的因此点M和它的在图像上映射点m 关系用单位矩阵H 联系。sm=H
因为r1r2是正交的,可以得出
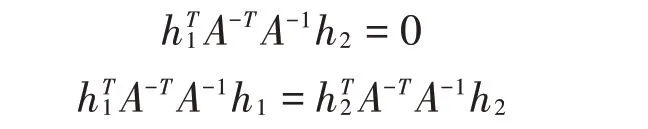
根据此矩阵求出封闭解。以上是同各国最小化代数距离获得,因此需要对它运用最大似然估计进行完善,最大似然估计可以通过函数求出最小值得到。
相机镜头产生的径向畸变也需要进行处理,先输入图像的中心点坐标,再运用了张氏标定法得到矫正后的图像主点,计算输出图像与矫正后图像的宽高缩放比映射到矫正后图像坐标,并将该坐标通过张氏标定法映射到输入图像坐标,然后用双线性插值进行优化,将源图像和目标图像集合中心对齐,把浮点运算转换成整数运算。
3 图像处理
图像处理也是视觉引导机器人运动过程中的一个重要环节,让机器人准确获取目标图像的形状特征才能正确指导机器人运动。在本系统中,运用halcon,首先进行灰度转化,先转为RGB 三通道,然后转为HSV 通道,以便于更好的选取选区;之后进行粗定位,对图像进行一次处理,大概找出定位区域,选取合适的通道在灰度直方图中进行阈值处理;然后进行精定位,一般画出ROI区域,进行二次处理;再次阈值,精确定位选区;做连通域,创建合适的结构元素,进行膨胀和取开运算得到A 图像;根据特征直方图多个特征取值,最后确定精确识别区得到图像B;取AB交集得到图像C;最后对图像C进行去燥,为后续机器人的抓取工作提供信息。
4 图像标定
图像处理完成后,对物体进行手眼标定,相机知道的是像素坐标,机械臂是空间坐标系,所以手眼标定就是得到像素坐标系和空间机械臂坐标系的坐标转化关系。在实际控制中,相机采集到目标物在图像中像素位置后,通过标定好的坐标转换矩阵将相机的像素坐标变换到机械臂的空间坐标系中,然后根据机械臂坐标系,计算出各个电机该如何运动,从而控制机械臂到达指定位置。
5 机械臂抓取
相机标定和图像处理及标定完成之后,得到了相机拍摄时物体的准确位置,此时需要引导机器人来抓取物体。将halcon中图像采集与处理的程序导出转化为C++格式,再将其程序在VS2010 中打开。此时将程序分为三个部分,第一部分是函数声明部分,第二部分是函数程序部分,第三部分是整体函数调用部分。这三部分程序在halcon内部编辑时所用到的算子在导出成为C++程序之后都变成了封装好的函数。为了使机械臂二次开发抓取所需的物体,本系统采用了SDK开发包在C++开发平台进行开发。将SDK包导入到新建的C++工程中,添加头文件,进行网络初始化,获取机械臂实例化,等待机械臂进行连接,对机械臂进行初始化、解锁、设置臂长,使机械臂运动抓取所需物体。
6 结语
相机相当于物体的“眼睛”,用相机对物体进行实时采集,可以解决由于外界环境变化时,机器人错误工作的问题。我们对物体进行位姿测量、相机标定、手眼标定、图像处理,最后再传送位姿至机械臂等一系列操作,引导机械臂完成物体抓取。在这过程中,会出现一些系统误差和随机误差,只有不断优化,减少系统误差和随机误差,直至接近理想化目标。

