基于高斯模型的心电特征提取研究

孙树平，杨文博，董增奇，张弼强，黄婷婷

南阳理工学院，河南南阳473000

前言

根据国家心血管中心组织所编写的《中国心血管病报告2018》［1］，我国居民心血管疾病致死连续多年位居中国居民非传染病死亡原因首位。2016年，农村因心血管疾病死亡人数占全部因病死亡的45.50%，城市心血管疾病死亡人数占全部因病死亡的43.16%。随着心血管疾病患病率及死亡率持续上升，2019年全国心血管疾病患者人数已达到2.9 亿。我国的心血管疾病防治工作正面临严峻挑战。

心电图是一种广泛应用于分析心脏功能基本生理信号的技术［2-3］。传统心血管疾病诊断治疗依靠患者的心电图记录，可供诊断的心电记录通常需30 min以上，短时心电记录不足以给医生提供足够诊断心血管疾病的信息。然而在长期心电记录分析中，逐个节拍检查是繁琐和费时的。因此，随着计算机技术、数字信号处理手段等技术的不断发展，借助计算机和数字信号处理手段对心电图信号进行检测、处理和分析已逐步取代传统诊断方式。然而无论是哪种分析方式，其诊断准确率都取决于心电特征提取的准确率。

长期心电记录中R 峰自动定位是诊断心脏疾病的重要步骤，R 峰定位的准确率直接影响到心电特征提取效率以及准确性［4-5］。国内外学者做了大量R 峰定位的研究，基于小波变换［6-7］、数字滤波器［8］、数学形态学［9］、导数［10］、S 变换［11］、全变分去噪［12］和自适应阈值［13］的R 峰自动定位方法被广泛应用。自动定位R 峰过程主要包含两部分：心电信号预处理和R 峰自动定位［14-16］。预处理过程是利用各种信号处理方法来增强QRS 复波群复杂度和抑制各种因素造成的噪声，然而大部分方法都存在缺陷，例如漏检和误检依赖于数字滤波器带宽的选择，使用小波变换时母小波的尺度选择也是难题。

在实际应用中，能有效同时提高或降低噪声的综合预处理技术是有难度的。一个肌肉的突然抖动或者是呼吸的变化都会引起心电信号波形变化。除了噪声之外，心电信号本身的多变性也给R峰的精准定位造成很大困难。例如负极性的R 峰、低振幅的QRS 复波群、R-R 间隔突然增宽或缩短、出现具有高能量T 波以及严重的基线漂移等，解决上述问题是R峰自动定位的重点。

本文提出一种基于高斯模型的心电特征提取方法，首先采用短时修正希尔波特变换（STMHT）算法自动定位R峰并对其进行修正，以求达到更高的准确率。在得到精确的R峰位置后，将连续的心电记录分割为独立的心电节拍。然后为每个节拍建立高斯模型，模型参数就是需提取的心电特征。

1 方法

心电特征提取可由图1所述内容进行阐述，其内容为：首先对心电信号进行预处理，其次对R 峰进行定位和修正，最后基于高斯模型提取心电特征；具体结构如图1所示。

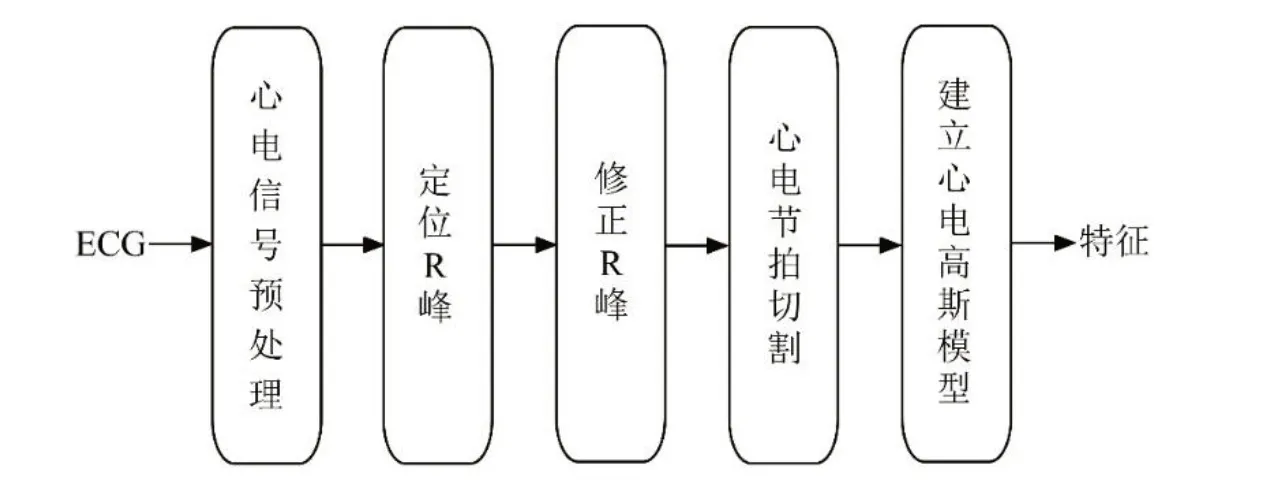
图1 心电特征提取流程框图Fig.1 Flowchart of electrocardiogram(ECG)feature extraction

1.1 心电信号预处理

本研究实验过程所采用的心电记录来自MIT-BIH心律失常数据库，它包含48组连续测量30 min的双通道心电记录，采样频率为360 Hz。这些心电记录包含正常的心电信号、高能量的P峰和T峰信号、负极性的QRS复波群、低能量的QRS复波群、时间间隔长的QRS复波群、振幅突然变化的QRS复波群、多种形式的室性早搏、长时间的停搏以及其它不规则的心率。

在心电信号测量中，由于采集设备以及采集个体差异性的限制等原因，最终得到的心电信号记录存在大量噪声，其波形存在不同的变化。影响R 峰自动定位的噪声主要有：工频干扰噪声、基线漂移噪声以及肌电干扰噪声等。预处理的最终目标是滤除心电记录中的噪声。工频干扰噪声是由市电系统所造成的噪声干扰；基线漂移噪声是在采集心电信号的过程中因采集人呼吸产生的噪声，基线漂移造成信号的突然变化，会拉高或降低P-QRS-T 波的振幅。基线漂移噪声频率受到呼吸频率的影响，通常集中在［0.05,2］（单位Hz）。肌电干扰噪声是由于在采集心电信号的过程中，被采集人肢体活动或其他情况造成采集电极区域肌肉电位变化产生的，肌电干扰噪声的形态非常杂乱，其频率范围较为广泛［1,1 000］（单位Hz）。为去除这些噪声，本文采用小波分解的滤波方法，保留心电信号频率在［11.25,22.5］（单位Hz）的成分以降低R峰定位的难度。心电信号原始波形如图2 所示，其去除基线漂移效果如图3 所示。

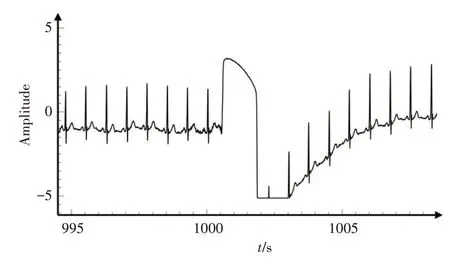
图2 心电信号原始波形图Fig.2 Original waveform of ECG signals

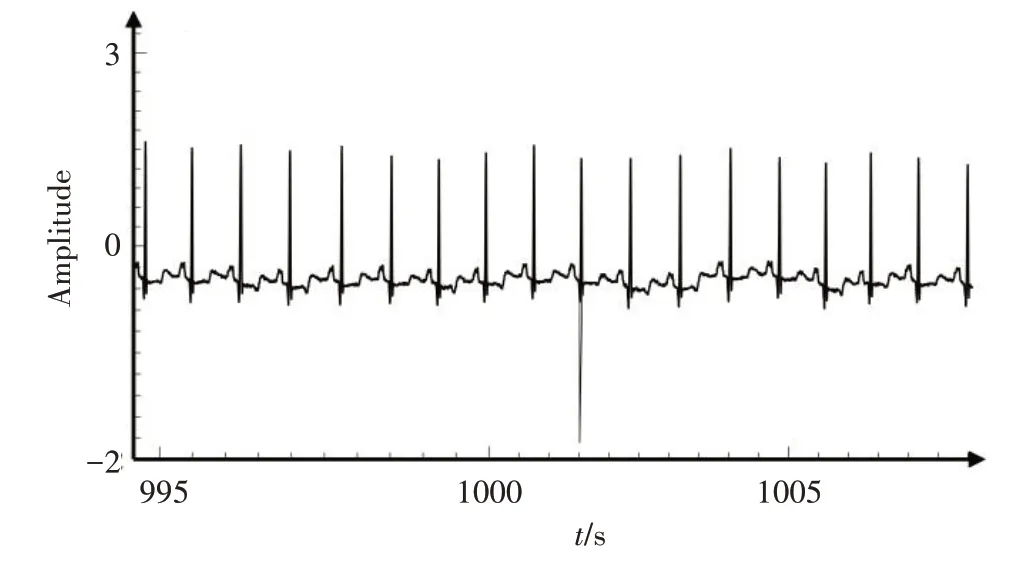
图3 心电信号去除基线漂移图Fig.3 ECG signals after baseline drift removal

1.2 定位R峰

心电信号特征提取的效率和准确率取决于R峰自动定位的准确率，为了获得精准的R峰位置，本文采用了一种STMHT的R峰自动定位算法［17］。在心电信号预处理后对经过滤波处理的原始心电记录进行平滑包络提取，然后通过希尔伯特变换的正过零点确定R峰位置。经实验验证，在原始心电信号图中采用希尔伯特变换正过零点所确定的R峰位置与数据库中给出的R峰注释位置存在一定偏移。因此笔者在希尔伯特变换正过零点所确定的R峰位置前后25个样本点内寻找正向能量最高的峰作为真正的R峰位置［18］。经算法自动定位的R峰与数据库中注释的R峰位置误差在100 ms以内即视为定位准确［19］。基于STMHT算法的R峰自动定位结果片段如图4所示。

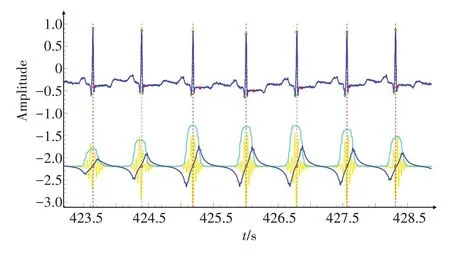
图4 心电信号R峰定位Fig.4 R-peak location of ECG signals

1.3 修正R峰

经过与注释位置的对比，本研究所采用的算法定位的R峰具有很高的准确率，但仍然存在少量的漏判R 峰、误判R 峰以及极性误判的R 峰，因此需对这些定位不精确的R峰进行修正。

1.3.1 增补漏判R峰经初步定位后R峰有时会出现漏判R峰现象，具体表现为漏判位置相邻两个R峰R-R间隔过大。由于心电信号具有不确定性，判断R-R间隔大小不宜采用固定阈值。本文采用统计学知识，统计整个约30 min心电信号的时间间隔并绘制箱形图，所有的上离群点即为R-R间隔过大的位置。根据箱形图所反映的结果，笔者有充分理由怀疑上离群点所对应的R峰与前一个R峰之间存在漏判R峰。

在找到漏判R 峰可能存在的位置之后则需要检测是否真的漏判以及如何增补。R 峰是每个心电节拍中能量最高、突变最快的特征波形，因此假设在离群点所对应点的R 峰与其前一个R 峰之间能量最高的峰为漏判R 峰。之后检验此R 峰是否为真正R 峰。在这里同样引用统计学知识，真正的R峰其能量值应该不小于其相邻两个R峰能量值较小R峰的0.36倍。假如此处R峰能量大于能量较小R峰的0.36倍，则此位置应添加一个R峰；反之则保留原状态。漏判R峰的记录片段如图5 所示。该片段内R-R 间隔的箱型图如图6 所示。添加漏判R 峰及判断添加的R 峰是否为真正的R 峰结果如图7 所示。图7 添加的4 个R峰经过再次判断后，能量值过低的3 个最终没有添加。

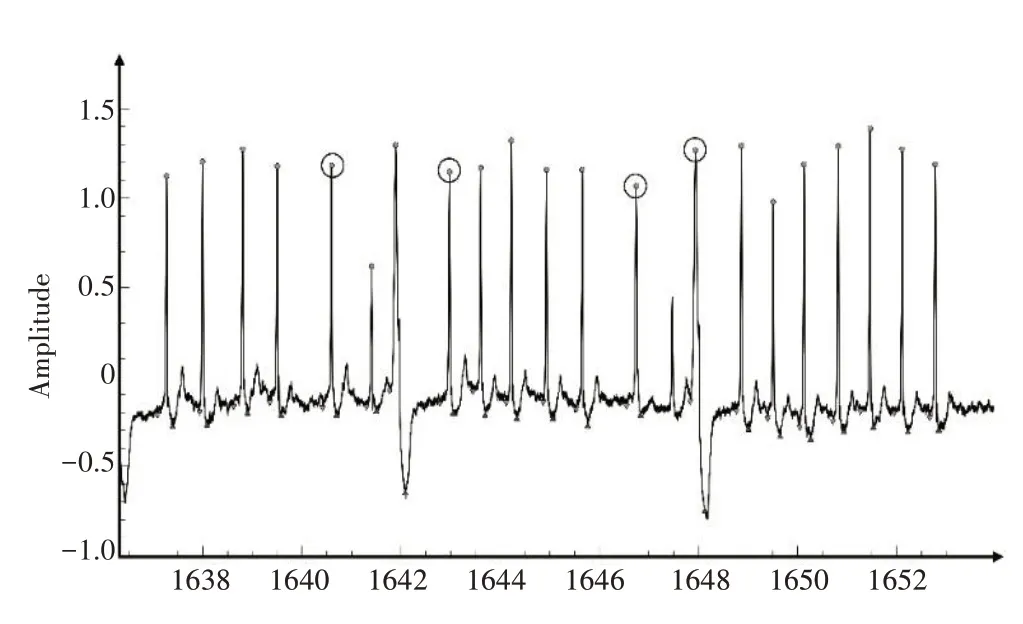
图5 漏判R峰示意图Fig.5 Schematic diagram of false negative R-peak

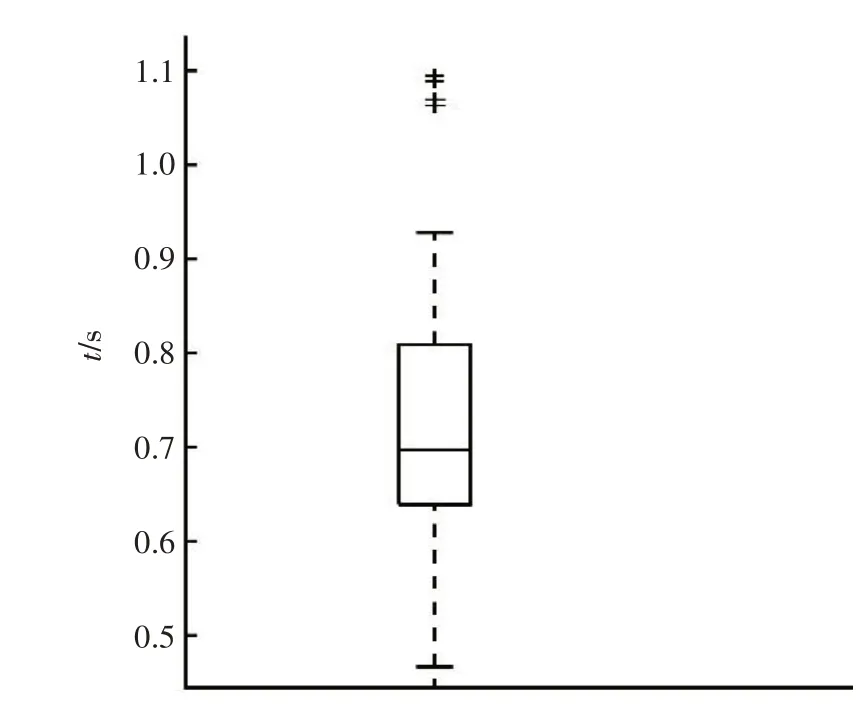
图6 R-R间隔箱形图Fig.6 Box-plot of R-R interval

图7 添加R峰示意图Fig.7 Schematic diagram of R-peak addition

1.3.2 删除误判R 峰除了漏判R 峰，另一个突出问题为误判R峰，具体表现为误判位置的R峰与相邻两个R 峰其中的一个距离过近。R-R 间隔是否过近利用生理不应期（即在0.25 s 内心脏一定不会跳动两次）进行判断［20］。当出现R-R 间隔小于0.25 s 时，必定有一个R 峰不是真正R 峰。通常R 峰是节拍中能量最高的峰，因此能量较小的R峰为误判R峰。在前文增补漏判R峰的过程中做过能量的判断，如果一个R 峰的能量小于相邻两个R 峰中能量较小R 峰的0.36 倍，则此R 峰不是真正的R 峰。即初步定位的R峰中能量较小的R 峰可能是误判R 峰。利用上述条件，检测整个完整的30 min 心电信号记录，将能量值过低的R峰删除。

如图8 所示为心电记录123 的片段，上方图是基于STMHT 算法定位R 峰的结果，虚线框所圈位置是误判R峰现象，虽然能量较低的R峰位置确实是过零点，但是其与后边的R 峰间隔只有118 ms，不满足生理不应期条件，在图中被删除。

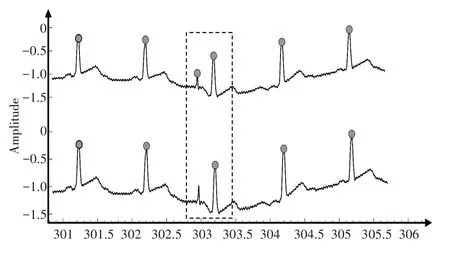
图8 删除误判R峰示意图Fig.8 Schematic diagram of deleting misjudged R-peak

1.3.3 反向R 峰修正在心电信号中会出现一些负极性QRS 复波群，这些位置的R 峰初步定位为正极性能量最大峰。这里引入Q峰、S峰、T峰辅助修正。极性误判分为R 峰和Q 峰错位以及R 峰和S 峰错位两种情况。前文已经提到通常在每个心电节拍中R 峰能量最高，然而在出现负极性的QRS 复波群时，能量最高的峰不一定是R 峰。因此利用各峰能量比例关系进行修正。

首先是R峰和Q峰错位，具体表现为初步定位的R 峰能量比Q 峰能量低。然而在负极性QRS 复波群中并非Q 峰能量高就可将R 峰漂移至Q 峰。通过将实验中得到的Q 峰和R 峰与MIT-BIH 心律失常数据库中Q 峰和R 峰标准位置对比统计分析，得出结论为：当Q 峰能量大于R峰能量1.85倍时将R峰漂移至Q 峰，反之则保留原状态。其次是R 峰和S 峰错位，其判断准则为：在S 峰能量大于R 峰能量的1.19 倍条件下，若R 峰能量是T 峰能量的0.96～1.50 倍，则将R峰漂移至S峰，反之则R峰和S峰保持原状态；在S峰能量小于R 峰能量的1.19 倍条件下，若Q 峰能量为T峰能量的2.15～29倍，则R 峰漂移至S 峰，反之则保留原状态。

如图9 上方图所示为心电记录221 的片段，可以看到出现了3个负极性的QRS波群，但是都被定位在了正方向，下方图即为修正示意图。

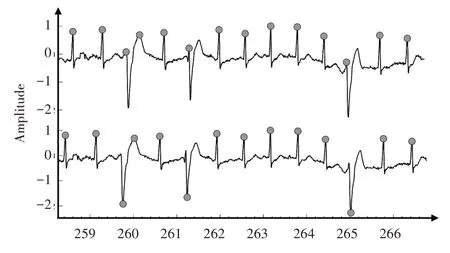
图9 反向R峰修正示意图Fig.9 Schematic diagram of reverse R-peak correction

1.3.4 流程框图基于高斯模型的心电特征提取流程图如图10 所示，流程图参数及意义如表1 所示。其中Ry、Qy、Sy、Ty分别为R、Q、S、T 峰的峰高（振幅），RQi为第i个心电节拍中R 峰与Q 峰振幅的差值，RSi为第i个心电节拍中R峰与S峰振幅的差值。

1.4 基于高斯模型的特征提取

图11a 是一个心电节拍的散点图以及由散点图拟合出的心电高斯模型。由于实验所采用的心电记录都是连续的心电记录，因此建立心电高斯模型应分为两个步骤：心电节拍切割和高斯模型拟合。

1.4.1 心电节拍切割每一组心电记录都是独一无二的，因为采集对象的年龄、工作环境、身体状况、采集设备、采集环境等都会影响到最终采集到的心电信号。以MIT-BIH 心律失常数据库中的心电记录为例，48 组记录同样是采集30 min 的连续心电记录，心电节拍最少的117 记录仅仅只有1 535 个节拍，而心电节拍最多的215 记录却有33 363 个节拍。目前使用较为广泛的方法是针对心电中基准点进行检测。首先对心电信号进行变换或滤波，突出心电的部分，然后通过基于自适应阈值的算法来识别基准点［21］。但是由于不同的心电记录在形态、能量以及持续时间方面的特点都存在很大的差异性，采用相同的检测方法检测所有的基准点具有很大的挑战性。本文不再利用检测基准点分割心电节拍，利用前文得到的R 峰位置，将所得R 峰间期按2：1 的比例切割［22］，切割点即为心电节拍起止位置。前文未曾引用的P峰即为Q峰前边1/3间隔位置中能量最高的峰。

1.4.2 建立心电高斯模型将经过R 峰自动定位的心电信号进行精准的心电节拍切割后，利用高斯函数对每一个心电节拍进行曲线拟合，将心电记录统一为一维多元高斯函数。下面将介绍高斯拟合算法。

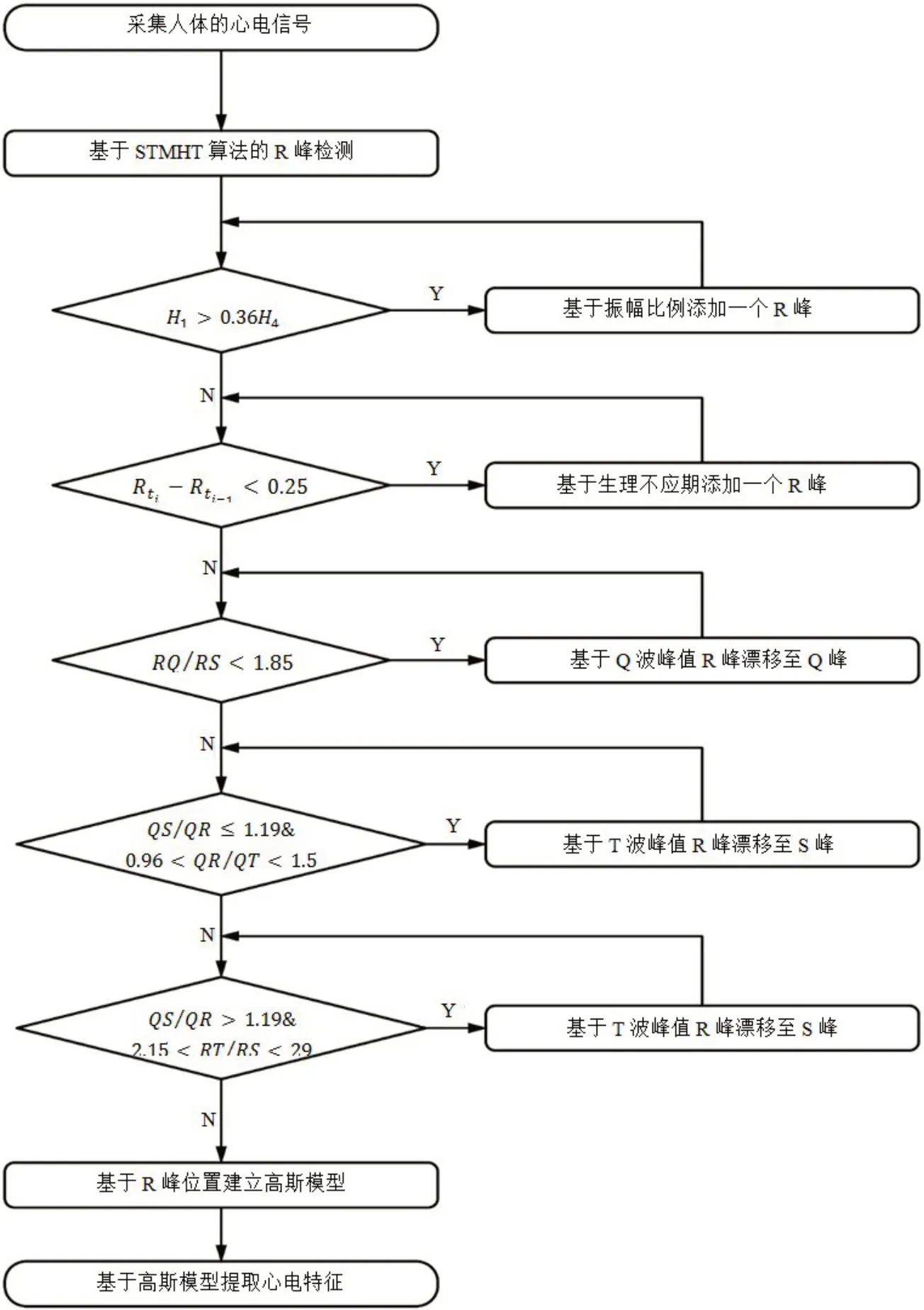
图10 心音特征提取流程图Fig.10 Flowchart of ECG feature extraction

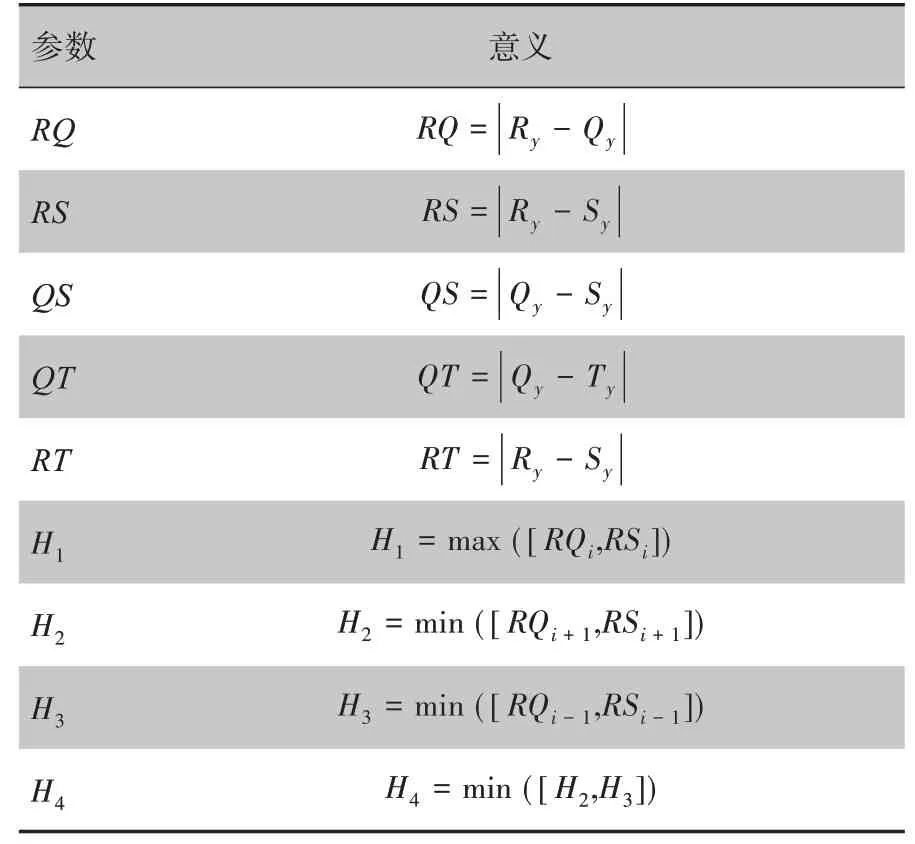
表1 流程图参数及意义Tab.1 Flowchart parameters and the corresponding meaning

高斯拟合算法原理：

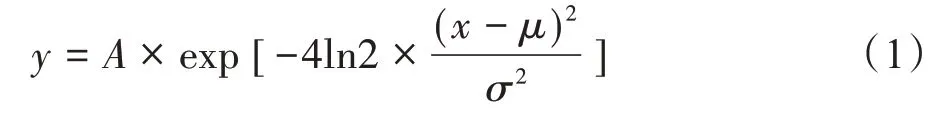
其中，A为峰高，μ为峰的中心，σ为高斯曲线的半高宽度，简称峰宽。对式（1）取对数：

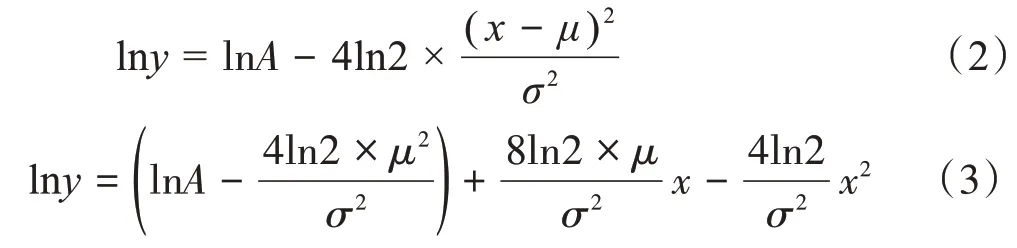
将函数系数分别设为b1、b2和b3，则：

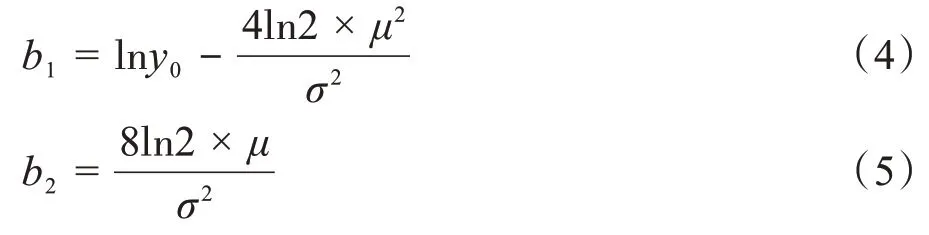
图11 心音节拍的高斯模型示意图Fig.11 Schematic diagram of the Gaussian model of ECG beat

因此式（2）可以表示为：

高斯函数拟合表示为：

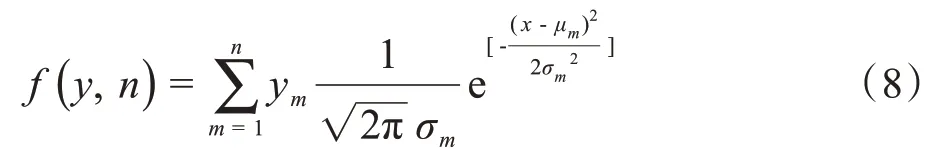
若y的数据长度为n，则式（6）表示为：

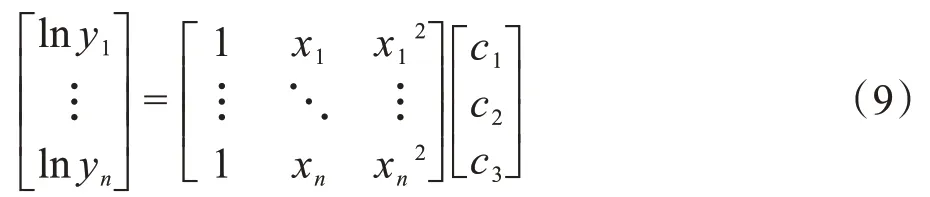
计算可得：

1.4.3 心电特征提取为每个心电节拍拟合高斯模型之后，心电信号特征波形P 波、QRS 波和T 波的位置已经确定，此时可以进行精确的特征提取。主要特征包括R-R 间隔、QRS 复波群宽度、R 峰幅值、P-T 间隔以及Q-R 间隔和Q-S 间隔。根据心电记录105 的一个心电节拍建立高斯模型如图12 所示，所提取的特征参数如表2 所示。图11b 是P 波、QRS 波和T 波的高斯模型，提取3个模型的参数即为心电特征参数数据。

2 实验结果与分析

2.1 R峰定位结果

根据定位的结果以及国内外参考文献，计算了3个定量结果：通过算法定位正确的R峰（TP）、通过算法未定位到的R峰（FN）和通过算法定位错误的R峰（FP）。评估R峰自动定位算法的性能参数有灵敏度（Se）、正预测值（+P）和检测错误率（DER），通过下式计算：

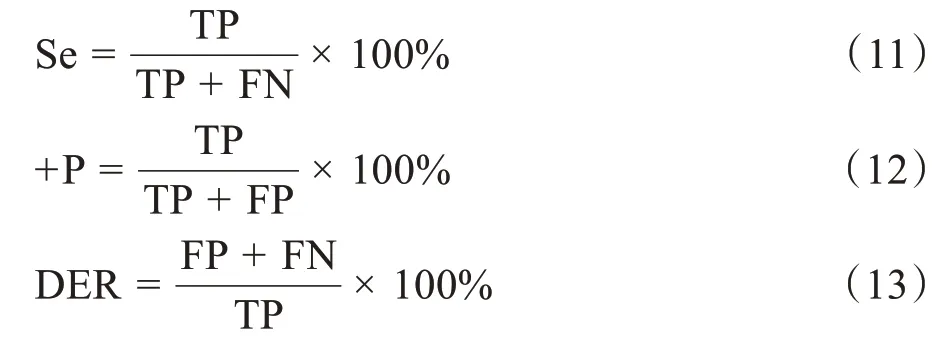
算法的整体性能是通过检测精度（ACC）来衡量的，检测精度的定义为：

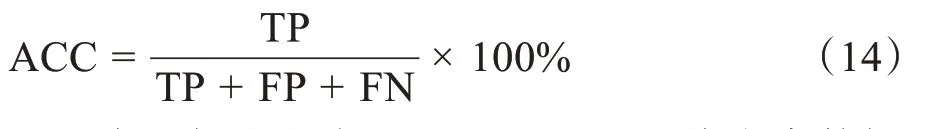
通过本文提出的方法对MIT-BIH 心律失常数据库的原始心电图记录进行R 峰自动定位。该方法产生79 个漏判R 峰和140 个误判R 峰，总共定位错误219 次。但是根据正常心电记录和病理心电记录特点的差异，以及信号噪声的不同，心电图记录个体定位准确率从98.99%到100%不等。

2.2 特征提取结果

如图12 所示为心电记录105 的片段拟合高斯模型结果图。从图中的结果来看，拟合出的高斯模型和原始记录近乎完全相同。高斯模型的参数有峰高、峰位和峰宽，对应到心电信号中即为振幅、位置和持续时间。图12 中模型部分参数如表2 所示。对应到心电信号中分别是每个节拍的P 波、T 波和QRS波群的峰高A、峰的中心μ和峰宽σ。

图12 拟合高斯模型结果图Fig.12 Result of fitted Gaussian model

3 结论

本文采用MIT-BIH心率失常数据库对本文研究进行验证，其中R峰平均检测精度为99.80%，并确定了以6个高斯函数为每个心电节拍建立模型，其获得的模型拟合相似指标达98.90%，从而利用高斯模型的参数定义并提取每个心电节拍特征数据。本研究后续将采用机器学习算法对心电特征进行模式识别，进而为医护人员提供更为直接的心脏病诊断参考信息。

表2 高斯模型参数Tab.2 Gaussian model parameters