青光眼药物跨角膜输运数学模型及特性分析

黄飞，徐洪涛，雷苑，屈治国

1.上海理工大学能源与动力工程学院，上海200093；2.复旦大学附属眼耳鼻喉科医院，上海200031；3.西安交通大学能源与动力工程学院，陕西西安710049

前言

青光眼是导致人类失明的三大致盲眼病之一，对青光眼的治疗最普遍的一种治疗方法是局部用药。局部用药是通过滴注眼药水或涂抹眼药膏等方法将药物施于眼表层，药物透过角膜进入眼球前房区域，对前房区域内病变组织进行作用［1-2］，具有低渗透特性的角膜组织是药物从眼表进入前房最主要的屏障。此外，结膜和巩膜的吸收作用也会使得药物进入体循环，药物毒性会对全身造成不利影响［3-5］。因此，为使药物能够在尽可能短的时间内进入前房达到用药剂量并减少对全身的毒副作用，亟需展开对青光眼局部用药后药物跨角膜输运特性的研究。

针对药物跨角膜输运这一过程可以建立遵循特定物理规律的数学模型。首先需要了解药物跨角膜输运过程的主要机理和影响因素，忽略次要因素，得到简化的数学模型。对于输运特性问题的主要研究方法有实验研究和借助数学模型研究。对眼药制剂渗透角膜的实验研究已有很多，但主要集中在不同药物制剂的理化性质对渗透效果的影响。张湘晖等［6］对新目安眼用凝胶剂等4种不同化学成分眼药制剂进行离体角膜渗透性试验，取药物跨角膜累积渗透最大量70%所需要的时间作为角膜渗透速度参数，得出新目安眼用凝胶制剂角膜渗透速度是目安眼用凝胶制剂的3.452倍。赵雯等［7］以离体角膜扩散实验研究了不同质量分数的3种环糊精对姜黄素角膜渗透性的影响，得出不同质量分数的3种环糊精作用下姜黄素的表观渗透系数。以上研究并未能建立相应的数学模型用以药物跨角膜输运更广泛的研究。对于眼部建模仿真的研究进展国内已有赵亚丽等［8］进行，得出人眼建模仿真的研究深化了对眼部生理学和病理学的认识，总结了人眼建模仿真的重要发展趋势。借助数学模型进行药物跨角膜输运特性的研究也已展开，例如，在药物代谢动力学领域，早期的单室模型和多室模型已被广泛用于研究药物输运；Zhang等［9］和Edward等［10］提出了一种类砖模型，对药物跨角膜输运过程与机理进行了研究；Pak等［11］利用一种准三维的计算生物学方法研究了药物的跨角膜输运。单纯的模型建立在没有实验相结合的情况下略显单薄。进行实验与数学模型相结合的研究还不是很多，Gupta等［12］借助实验拟合出一种药物输运的控制方程，对角膜的非均质性做了研究，包括了药物-细胞结合分布动力学，角膜组织交界界面对输运的抗性和细胞内的输运动力学。然而以上研究未能充分分析不同给药方式对药物进入眼球前房通量以及累积量的影响。

因此，本文基于前期的青光眼药物跨角膜输运实验，修正基于菲克第二定律的药物输运数学模型，分析了表面药物浓度、扩散系数、给药方式对药物累积的影响，以期为后续更加深入地研究药物跨角膜输运机理提供理论指导。

1 青光眼药物跨角膜输运实验简介

1.1 实验方法及原理

考虑到采取活体实验会受到眼内房水流动等对药物清除作用的影响，使得实验难以获取药物跨过角膜的累积量，因此本文采取离体实验的方法。本实验选取最经典，至今有140多年历史且应用广泛的毛果芸香碱作为研究跨角膜输运特性的实验药物，角膜选取厚度0.2 cm的新鲜猪角膜。

实验采用Franz扩散池对猪角膜进行毛果芸香碱水溶液的药物渗透角膜离体实验。在扩散池的供给池部分中加入预先配置好的毛果芸香碱水溶液，为减少实验误差，对比不同给药浓度下药物跨角膜输运特性，实验分别配制了1%、5%［质量分数为ω=0.01（1×104μg/mL），ω=0.05（5×104μg/mL）］两种浓度的毛果芸香碱水溶液作为实验药物试剂。在接收池中精准加入19 mL的PBS溶液（磷酸二氢钾KH2PO4）作为接收液，并保证接收液与角膜间完全接触无气泡。

为减少实验误差，实验中ω=0.01质量分数药物制剂进行3组实验，如图1中第1、2、3组实验；ω=0.05质量分数药物制剂进行2组实验，如图1中第4、5组实验。每组实验加入的毛果芸香碱水溶液为300 μL。

如图1 所示，所有实验用Franz 扩散池置于透皮试验仪内进行水浴加热，温度维持在37°C。在透皮试验仪的作用下保持接收池内药物的均匀分布。在实验非采样期间为减小蒸发给实验带来的误差，供给池与接收池的开口用密封条封住。

图1 透皮试验仪Fig.1 Transdermal device

分别在给药的5、10、30、60、90、120、180、240 min后抽取接收液4 mL 置于取样瓶中，每次抽取后向接收池补充4 mL的PBS溶液。对不同时间点接收池内药物浓度的测量通过高效液相色谱法测量得出，本高效液相色谱法参考陈滨等［13］实验过程完成。

1.2 实验结果

参考陈滨等［13］实验过程，本文得到毛果芸香碱标准溶液的峰面积（y）与浓度（x）（μg/mL）标准曲线方程为式（1）：

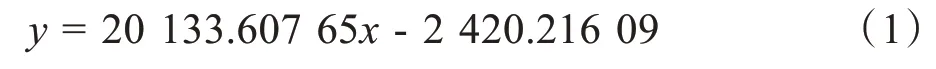
通过对5 组实验不同时间点下采集的接收池内样本溶液峰面积的获取和标准曲线方程的计算可得到相应时间点下接收池内毛果芸香碱的药物浓度，分别对第1、2、3 组和第4、5 组同时间点取样的药物浓度结果求平均值，并将得出的平均值除以角膜面积，得到单位面积下的药物浓度结果值，后文中的药物浓度及累积量均对应单位面积情况。

根据药物在接收池内的浓度及每次采样量，利用式（2）计算药物在不同时间内透过单位面积角膜在其另一侧的药物累积量：

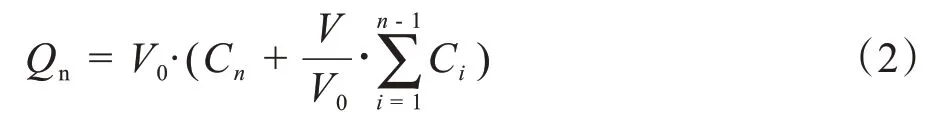
其中，Cn表示t时间点测得的接收池内药物浓度，μg/mL；Ci表示t时间点前一时间点测得的药物浓度，μg/mL；V0表示接收池中内溶液的总体积，19 mL；V表示每次的取样体积，4 mL。其计算结果见表1。

表1 药物累积量随时间变化实验数据表Tab.1 Experimental data of drug accumulation over time

根据实验结果，参考Xu等［14］对药物透皮扩散阶段的研究，可以得出药物累积过程分3个部分，取ω=0.05实验组的药物累积量变化曲线进行过程分析，分析图解如图2所示。图2是根据实验结果拟合出的曲线，曲线共分3个部分：第一部分称为非稳态阶段，此阶段药物在角膜内的分配未达到平衡；第二部分称为伪稳态阶段，该阶段内药物在角膜内的分配达到平衡，药物累积过程成线性增长，为对比与其他两个部分的不同，特将第二部分的曲线两段延长，如图中黑色直线所示；第三部分阶段的药物累积速率变慢，造成这一结果的主要原因是随着渗透时间的增加供给池内药物减少，药物已经无法完全覆盖角膜，药物供给不足。

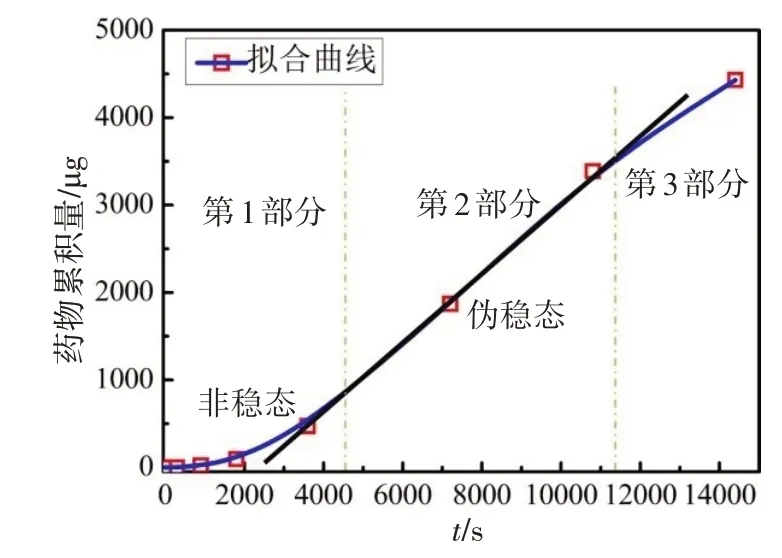
图2 药物累积量曲线分析图Fig.2 Curve analysis of drug accumulation

根据Xu等［14］在进行药物透皮扩散研究时采用的时滞方法分析，可以计算出毛果芸香碱水溶液跨角膜输运过程中的扩散系数大小约为2.47×10-6cm2/s。

2 数学模型

2.1 药物跨角膜输运数学模型

药物分子在角膜组织中的输运是一个包含多种生命活动的极其复杂的一个过程。图3 将角膜简化为一个三层区域的多层结构，把药物跨角膜输运视为药物在一个三层结构区域内的扩散过程。该简化符合角膜的生物学组织组成特征，对药物输运规律的研究不会产生严重影响，且可以提供理论分析指导。局部给药后，药物从眼表泪膜开始向眼内扩散，经过角膜上皮、基质和内皮直到穿透角膜，到达前房并在前房内累积。

图3 药物输运示意图Fig.3 Schematic of drug delivery

为了建立药物跨过角膜组织以及药物到达前房进行累积的输运过程的基本微分方程，引入了以下假设：（1）局部给药后，存留在泪膜上的药物充足，且在眼表泪膜处的药物浓度分布均匀，不受重力、温度等外界环境因素影响，忽略结膜、巩膜对药物的吸收，眼表泪膜处药物浓度保持恒定值C0；（2）初始阶段，角膜及前房内药物浓度为0；（3）药物在角膜各层组织内的扩散系数为恒定值；（4）药物透过角膜进入前房满足“漏槽效应”［14］，即，药物进入前房后会迅速被房水带走，角膜内皮与房水接触位置上不存在药物滞留，即角膜内皮最内侧位置的药物浓度始终保持为0；（5）药物扩散只有从眼外扩散到眼内一个方向，所以是一维的。

基于菲克第二定律，描述药物在角膜组织内的瞬时扩散过程偏微分方程为：

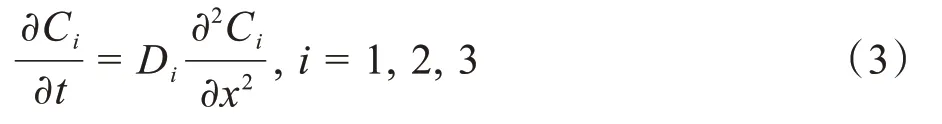
式中，Ci是药物浓度，Di是扩散系数，下标i=1,2,3分别代表角膜上皮、基质和内皮。在每层角膜交界处，两侧通量相等，即：

式中，下标12、23 分别代表角膜上皮和基质，基质和内皮不同层之间的交界面。

扩散通量J由菲克第一定律进行计算：

根据上述假设，可得到数学模型的初始与边界条件如下：

初始条件：

边界条件：

由于角膜被分成3层，角膜的上皮、基质、内皮分别对应着3 个扩散系数D1、D2和D3，因此角膜整体的等效扩散系数Dcor可表示为：

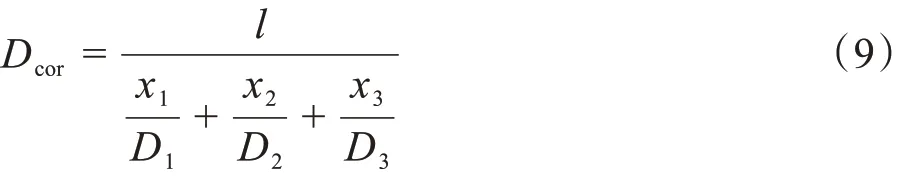
其中，l、x1、x2、x3分别表示角膜整体厚度，上皮、基质及内皮厚度。

利用等效扩散系数，药物通过整个角膜的等效扩散方程为：

基于上述初始条件和边界条件，式（10）中的药物浓度分布解析解为：

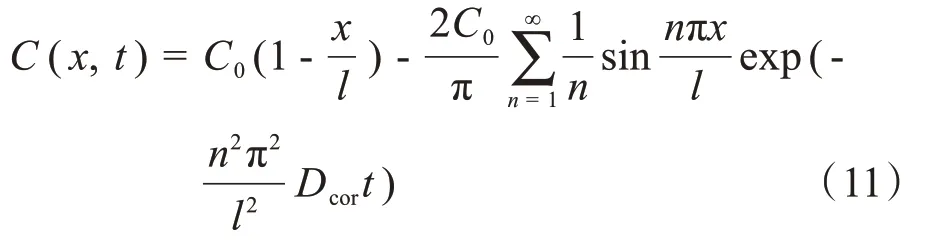
根据菲克第一定律，将式（11）代入式（5），可计算药物在角膜内皮与房水交界处的药物输运通量为：

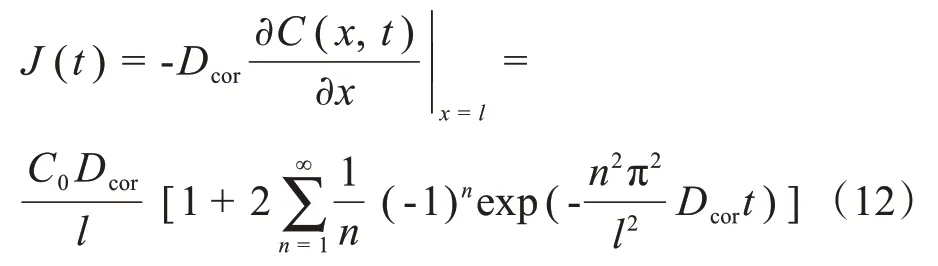
将式（12）对时间积分，得到药物通过单位面积角膜进入前房的累积量：

将式（12）代入式（13）后可得药物随时间改变在前房内的累积量数学表达式为：

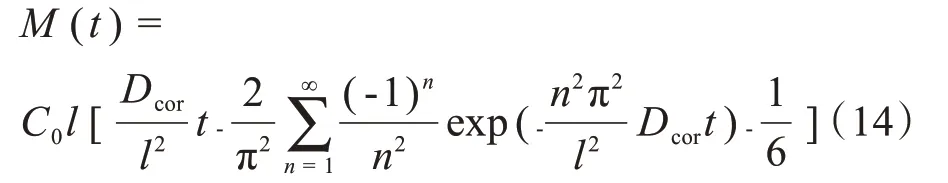
2.2 数学模型修正

根据第一节中的实验已知毛果芸香碱水溶液跨角膜输运的扩散系数（Dcor=2.47×10-6cm2/s）以及角膜厚度（l=0.2 cm）。图2表现的药物累积量拟合曲线前两个阶段是满足式（14）的变化规律，因此根据实验数据，修正式（14）中的参数，即可得出与实验结果匹配良好的数学模型，模型计算结果与实验数据对比如图4 和图5 所示。结合式（14）与式（10）的关系可以得到毛果芸香碱水溶液跨角膜输运的数学模型为式（15）：

其中，a表示角膜厚度修正参数；b表示扩散系数修正参数。针对毛果芸香碱水溶液，根据实验结果拟合得到参数a=0.9，b=0.64。

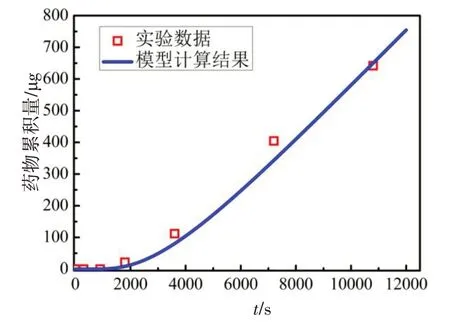
图4 数学模型与ω=0.01实验组结果对比图Fig.4 Comparison of mathematical model and experimental results of ω=0.01

图5 数学模型与ω=0.05实验组结果对比图Fig.5 Comparison of mathematical model and experimental results of ω=0.05

如图4和图5所示，分别是在给药浓度为1×104μg/mL与5×104μg/mL，扩散系数Dcor=2.47×10-6cm2/s，角膜厚度l=0.2 cm的条件下，实验结果与数学模型计算得出的药物累积量—时间关系曲线对比图。图中蓝色曲线是数学模型计算结果，红色点是实验结果数据。

3 药物跨角膜输运特性分析

局部用药的最终目的是使药物能够跨过角膜进入前房区域，从而作用于前房区域内的病变组织。基于以上修正的数学模型，图6给出了相同的眼表给药药物浓度（C0=5×104μg/mL），不同扩散系数（其中1倍的D=Dcor=2.47×10-6cm2/s，在后文中为方便分析，D即代表Dcor）影响下药物在前房内的累积量变化规律。图7 给出了相同扩散系数（D=2.47×10-6cm2/s），不同表面药物浓度（其中1 倍的C0=5×104μg/mL）影响下药物在前房内的累积量变化规律。

图6 药物累积量随扩散系数变化曲线图Fig.6 Graph of drug accumulation with diffusion coefficient

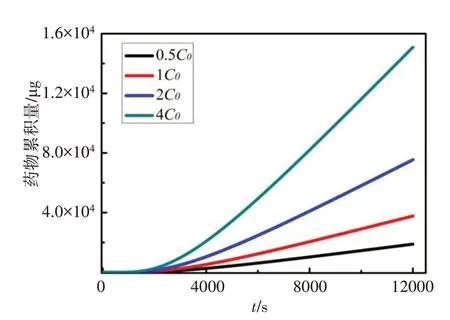
图7 药物累积量随药物初始浓度变化曲线图Fig.7 Graph of drug accumulation with initial drug concentration

由图6 可知，在表面药物浓度恒定时，对比0.5D与4D两种情况，药物累积量在60 min后分别为42和4 798 μg，相差10 倍以上，在200 min 时分别为1 233和19 551 μg，相差约15 倍。对比0.5D与4D两种情况，药物累积量在30 min 时虽然在图片中难以辨别差距，通过查阅相对应的计算数据可知两者相差1 000 倍以上，造成如此大差距的原因是30 min 时0.5D组的药物还处在非稳态阶段，即药物累积缓慢增长，没有进入线性增长的伪稳态阶段，药物累积速度较慢。因此可以得出扩散系数的提高可以明显缩短药物输运从非稳态到伪稳态阶段的时间，提高相同时间内药物跨角膜输运的累积量。

对比图7 中0.5C0与4C0两种情况，在当量扩散系数不变的情况下，药物累积量在30、60、200 min 相差均为8 倍，与初始给药浓度无关。因此，综合考虑高药物浓度可能对角膜及全身（结膜及巩膜会吸收药物进入体循环）带来的药物毒性，提高扩散系数是药物设计中重要的研究方向。

以上对药物输运特性的分析是基于角膜外表面给药浓度不发生变化的理想情况进行的，而在实际给药过程中，药物会受到给药形式的影响。除了以上提到的一种药物浓度不变的给药方式外，本文还将根据实际给药情况对比分析另外两种不同的眼表给药方式。第二种给药方式是以眼药膏形式给药（例如以热固凝胶为药物载体的情况［15］），在这种情况下眼表药物浓度半衰期为1 818 s［16］，因此角膜外表面药物浓度Ccor随时间变化的函数关系如方程（16）［17］：

其中，C0是Ccor的初始浓度，α=-0.000 38。

第三种给药方式是以眼药水的形式给药，且此时受到泪液对药物的清除作用。这种情况下眼表药物浓度则有更短的半衰期177.7 s［16-18］，因此角膜外表面药物浓度Ccor随时间的函数关系同式（16），其中α=-0.003 9。在式（16）中，指数函数的时间参数α是由ln(2)除以相应的半衰期计算得到的［17］。对于第一种给药方式则α=0。在C0=5×104μg/mL，D=2.47×10-6cm2/s的条件下，3 种不同的给药方式下药物经角膜进入前房的药物输运通量随时间变化曲线如图8所示。

图8 药物通量随时间变化曲线图Fig.8 Graph of drug flux over time

图8中绿线表示第一种给药方式，即角膜外表面药物浓度为恒定常数C0，这是一种理想条件。可见第一种方式药物通量会先增加再趋于一个稳定值，约0.45 μg/(cm2∙s)。红线表示第二种给药方式，即角膜表面施用眼药膏，蓝线表示第三种给药方式，即在角膜表面施用眼药水且受到泪液的清除作用。与第一种给药方式不同，第二种给药方式下药物通量会先升高到一个峰值而后下降，最后趋向于0，而第三种给药方式下药物通量变化规律相同，随着时间推移也将会趋向于0。造成与第一种给药方式下不同的药物通量变化规律的原因是眼表药物浓度变化规律不同，在第二和第三种给药方式下眼表浓度会不断下降，而第一种给药方式是保持眼表浓度不变。在第二种给药方式下药物通量会在约60 min到达峰值0.17 μg/(cm2∙s)，在第三种给药方式下药物通量会在约35 min 到达峰值0.03 μg/(cm2∙s)。随着时间推移，后两种给药方式下眼表药物浓度都将向0衰减，这也导致了药物通量最后趋向于0。造成两者峰值及到达峰值时间不同的原因是药物在眼表浓度的衰减时间不同，泪液的清除作用下，大部分以水溶液形式的药物很快从角膜表面清除，而以药膏形式的药物不会被泪液迅速清除而在角膜表面停留一段时间，药物可以缓慢持续释放进入眼内。

由于不同给药方式使得药物进入前房的药物通量变化不同，药物在前房区域的累积也有所不同，如图9所示。从图中可以看出，理想状态下的第一种给药方式会使前房内药物累积量持续升高，第二和第三种给药方式下药物累积量增长到一定数值后会缓慢趋于平稳。

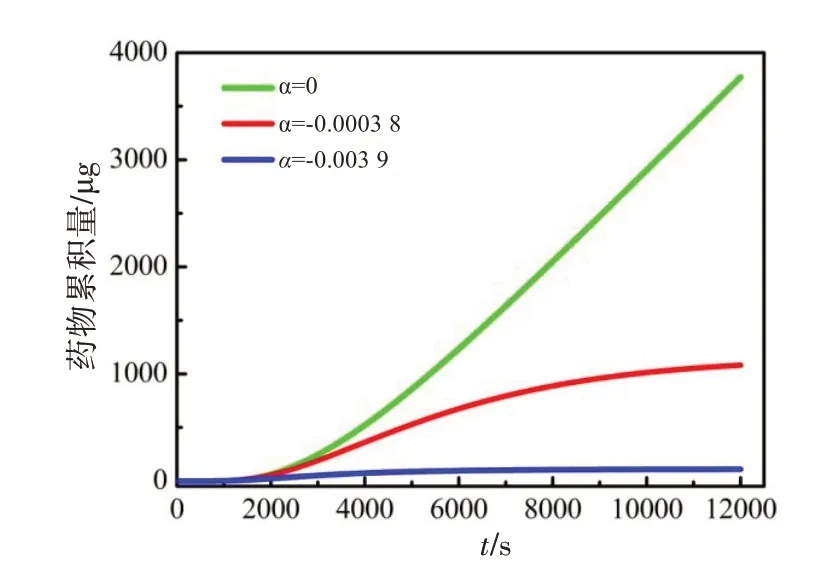
图9 不同给药方式下药物累积量变化曲线图Fig.9 Graph of drug accumulation with different administration modes

4 结论

通过对两种不同质量分数青光眼药物毛果芸香碱水溶液对角膜的离体渗透实验，将药物跨角膜输运过程分成了非稳态和伪稳态两个阶段。首先，根据实验结果修正了药物跨角膜输运数学模型。其次，通过对修正的数学模型进行理论分析，得出了扩散系数的提高不仅可以缩短药物输运从非稳态到伪稳态阶段的时间，也可以有效提高相同时间内的药物累积量，尤其在短时间内，高的扩散系数对药物累积量影响巨大。对比3种不同的给药方式，得出药物累积量随时间变化的不同规律及药物跨角膜输运过程中进入前房的药物输运通量达到峰值的时间及峰值量。