基于小波包变换的癫痫脑电棘波检测

朱宁宁，李皓，邓小乔，于明，李效龙

1.江苏科技大学电子信息学院，江苏镇江212000；2.江苏大学附属医院神经内科，江苏镇江212000

前言

癫痫是多种病因引起的慢性脑功能障碍综合征，主要是由大脑神经细胞群反复超同步放电而引起的，具有突发性和短暂性脑功能障碍等特点，会引起患者认知功能损害和情绪障碍。癫痫患者脑电信号中会出现棘波、尖波、棘慢复合波、尖慢复合波等异常波形。由于棘波幅度大、电位短、垂直上升和下降等瞬态特征，使得癫痫脑电信号中棘波的检测具有临床诊断意义。常见的棘波波形多为负相棘波，有时也为正相棘波，还有双相、三相棘波等，具体波形如图1所示［1］。

目前常用的癫痫发作检测算法有形态成分分析［2］、独立分量分析［3］、小波变换［4］、希尔伯特黄变换［5］、频率小波变换和支持向量机［6］、递归量化分析与支持向量机［7］、非矩阵分解［8］、奇异值分解［9］、深度卷积网络［10］、改进遗传算法［11］、稀疏表示［12-16］等。

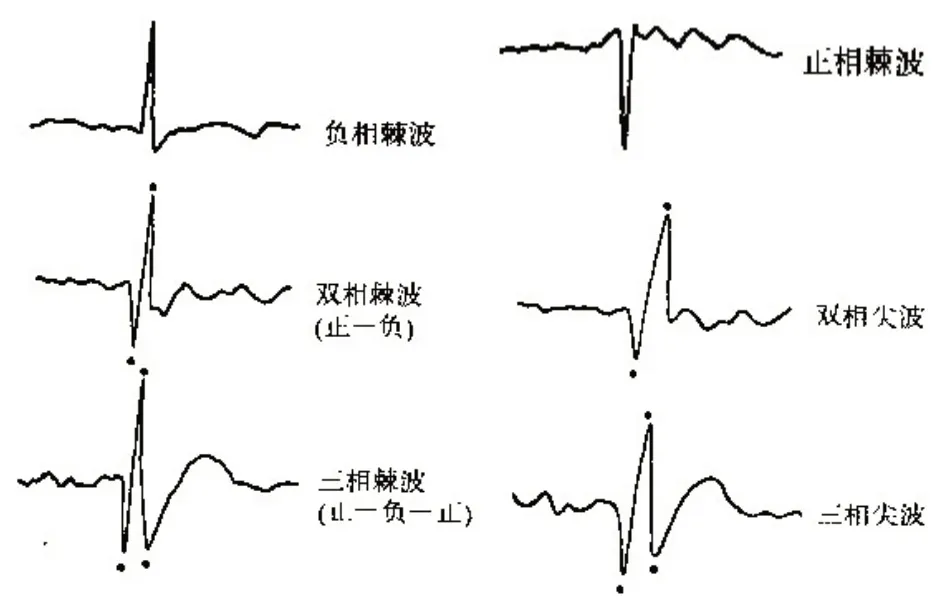
图1 不同形态结构的棘波Fig.1 Spikes of different morphological structures

癫痫发作检测要求脑电信号在特定的时间段或频率段有尽可能高的频率或时间分辨率，同时要求较高的棘波检出率以提高检测准确率。本文结合小波包变换可以多层次划分信号频带，对癫痫脑电信号进行3层小波包分解得到每层的脑电波频率带，然后重构脑电频率范围内关键节点频率的癫痫脑电信号，最后再结合棘波的幅度特征提取出癫痫患者在不同时期的棘波。

1 棘波检测算法

1.1 棘波检测步骤

小波包变换不仅可以很好地表征以低频信息为主要成分的癫痫脑电信号，还能够对信号高频部分进行更精细的分解，并且可以依据信号特点自适应的选择对应的频带，使得信号的频带与频谱相匹配，从而提高信号的时频分辨率，因此是一种适用于癫痫脑电棘波检测的信号分析方法。采用小波包变换的棘波检测算法流程如图2所示。

1.1.1 癫痫脑电信号频带划分实验数据的采样频率为173.61 Hz，信号长度为23.6 s。根据奈奎斯特采样定理可知，信号的采样频率范围为0～86.80 Hz。对采集的癫痫脑电信号进行三层小波包分解得到脑电信号的频带划分，具体如表1所示。

1.1.2 重构特定节点频率的脑电信号从表1 可以看出，第三层小波包分解把采集的癫痫信号进行了更细致的分解。由于大部分脑电信号的频率范围在0～30 Hz，因为表1 中节点S（3,0）、S（3,1）、S（3,2）包含了所有脑电波的频率，也包括要提取的棘波频率，因此只需重构节点S（3,0）、S（3,1）、S（3,2）即能够最大程度上得到所要提取的癫痫患者棘波信号。

三层小波包分解如图3所示，小波包变换中的每一层信号都被分解成低频和高频部分[17]。例如信号S经过三层小波包分解之后可以表示为：

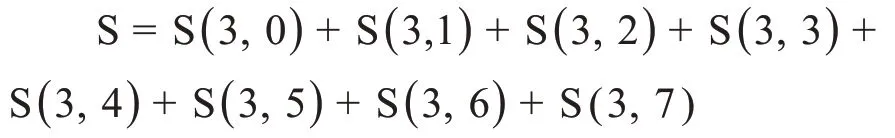
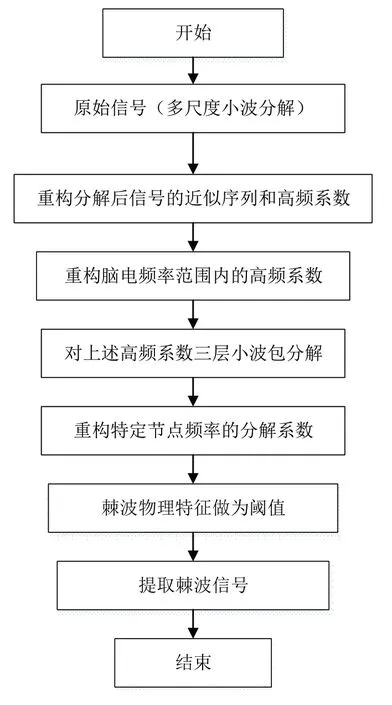
图2 棘波检测流程图Fig.2 Flowchart of epileptic spike detection

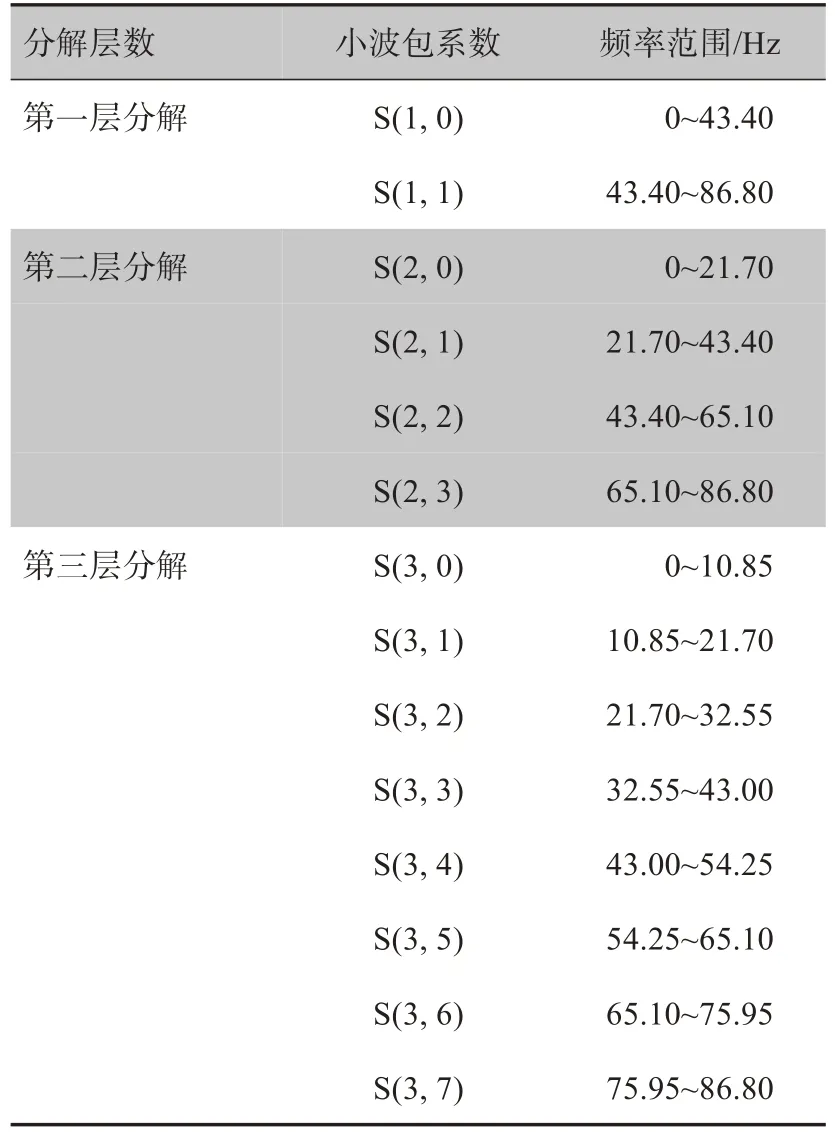
表1 基于小波包分解的脑电信号频带划分Tab.1 Electroencephalogram(EEG)signal frequency division based on wavelet packet decomposition

可见，信号S经过三层小波包分解后的子频带包含了原信号所有的细节频率信息。

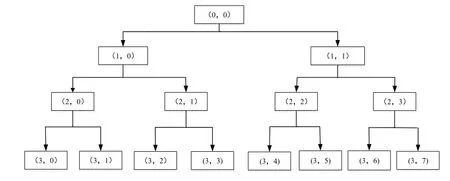
图3 三层小波包分解树结构图Fig.3 Diagram of 3-layer wavelet packet decomposition tree

1.1.3 棘波检测阈值选取棘波具有的明显的物理特征［18］，其中时限为1/50～1/14 s，放入脑电图测量尺14 Hz的刻度内则为20～70 ms，幅度多为100～200 μV。本文采用小波包变换对节点S（3,0）、S（3,1）、S（3,2）的脑电信号进行重构后，选择棘波信号的幅度作为阈值进行癫痫脑电棘波的提取。

1.2 小波包变换分解和重构

对脑电信号f(t) ∈L2(R)，设它的小波分解为：

fj(t) ∈Wj的小波级数为：

根据文献［19］给出的定理，对于每个j=1,2,…有：

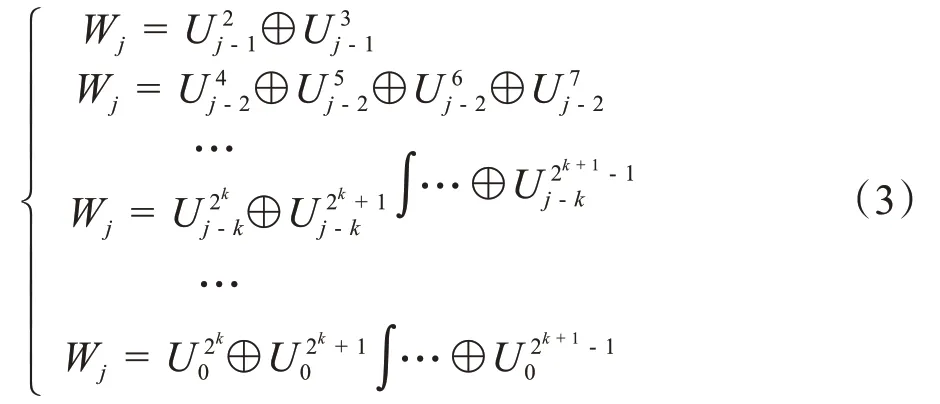
进而，对于每个m=0,1,…,2k -1,k=1,2,…，j和j=2,…函数族，有：

对于正交小波包，根据文献［19］给出的定理，∀k(1 ≤k≤j)和m(0 ≤m≤2k- 1),fj(t)∈Wj可以进一步分解成小波包分量的正交和，即：

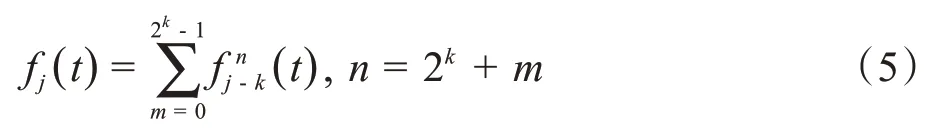
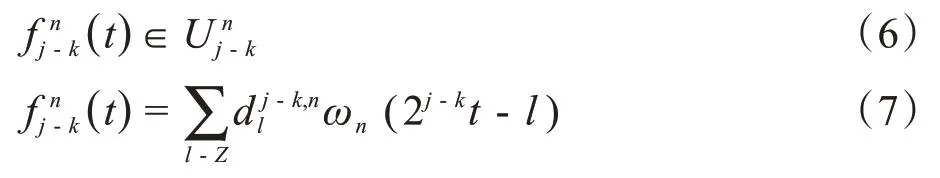
令k=0，则由式（6）可得f jn(t)∈U jn，式（5）可改写为：

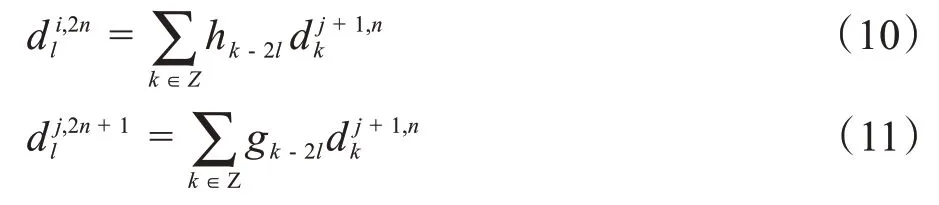
正交小波基定义：令ωn(t)满足下列尺度方程：

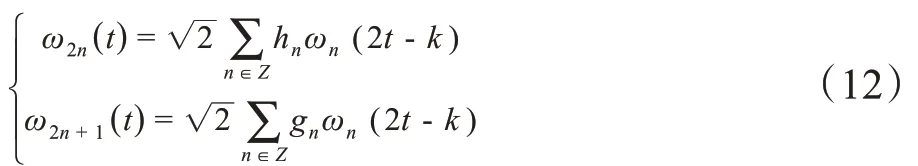
其中，n=0,1,2,…，系数序列{hn} 和{gn} 仍满足下列关系：

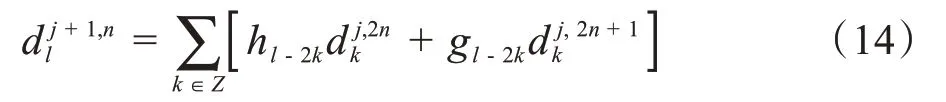
其中，h、g为滤波器系数，d为小波包分解系数，l、k为分解层数，j、n为小波包节点号。

2 实验及结果分析

2.1 实验数据描述

实验数据来自德国Born 癫痫脑电研究室。该数据库中共包含标号从A～E 的5 个数据集（表2），其中A、B 数据集是来自健康志愿者的脑电信号，C、D、E的数据集是癫痫患者手术前诊断并记录的颅内脑电信号。C、D 是癫痫发作间期采集的数据，E 是癫痫发作期采集的信号。每个数据集均包括100个采用10-20国际标准导联技术提取的单导联脑电信号。每个脑电信号的长度为23.6 s，采样频率为173.6 Hz。数据经过了一定程度的预处理，去除了明显的噪声和伪迹。仿真采用的数据包括患者癫痫发作期的数据、健康期的数据和癫痫发作间期的数据。实验的仿真平台基于Matlab2016b。

表2 德国Born癫痫脑电研究室数据Tab.2 Epileptic EEG data from Born epilepsy laboratory,Germany

2.2 仿真结果及分析

对癫痫患者a的脑电信号进行频谱分析（图4）和三层小波包分解（图5），然后采用本文提出的算法对癫痫患者a 在健康期、癫痫发作间期的脑电信号进行棘波提取，分别如图6 和图7 所示。因为癫痫发作期棘波出现的比较多，为了更准确的提取在脑电频率段出现的棘波，根据表1的脑电频带划分将癫痫发作期棘波的提取划分为节点频率（3, 0）的提取和节点频率（3, 1）的提取。为了检测该算法是否具有特异性（该算法是否对其他癫痫患者同样有效），分别将癫痫患者a 和癫痫患者b 癫痫发作期的数据进行对比，以验证该算法不存在特异性，分别如图8、图9、图10、图11所示。

最后根据仿真提取棘波的检测结果总结了5 个癫痫患者在不同时期的棘波检测数、误检数、漏检数以及相对应的各个时期的误检率和漏检率（表3）。

仿真结果分析如下所示。

图4 癫痫患者a健康期的脑电信号Fig.4 EEG signals of patient a in healthy period

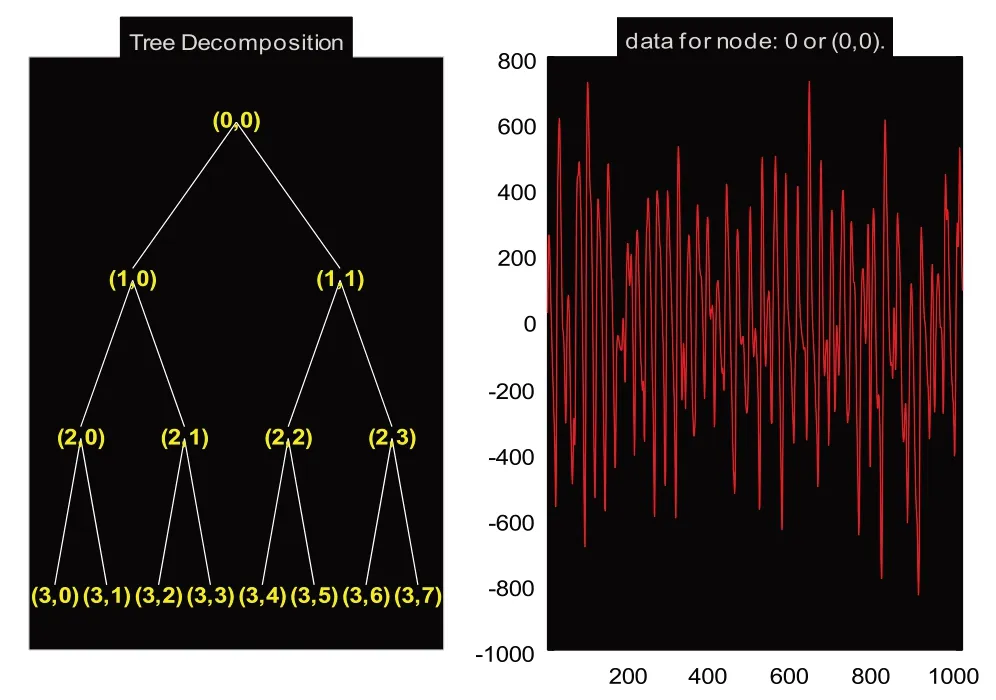
图5 小波包分解树结构及节点系数Fig.5 Wavelet packet decomposition tree and node coefficients

（1）由于仿真的数据已经过预处理，去除了噪声和伪迹，因此利用小波包变换和棘波的频率、幅度等物理特征相结合的算法不仅能提取出同一个病人在健康期、癫痫发作间期、癫痫发作期等不同时期的棘波；而且可以提取出不同患者在癫痫发作期的棘波，证明该算法适用于不同癫痫患者的棘波检测，不存在特异性。

（2）癫痫患者脑电中的棘波主要以爆发式节律出现。由健康期、癫痫发作间期、癫痫发作期相应节点检测出的棘波可以发现棘波主要出现在0～22 Hz频率段。所提取出的棘波波形包含参考文献［14］所指出的14 Hz 或6 Hz 的正相棘波，当然这里的6 Hz通常指5～7 Hz 也包含13～17 Hz，而且各自以独个连续爆发的形式出现。

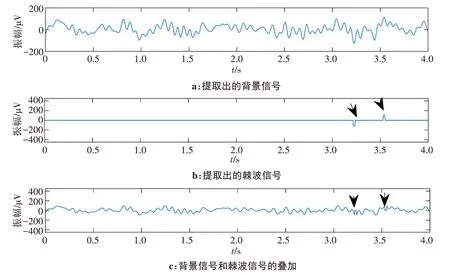
图6 癫痫患者a健康期脑电信号处理Fig.6 EEG signal processing of patient a in healthy period

图7 癫痫患者a发作间期脑电信号处理Fig.7 EEG signal processing of patient a in intermittent period

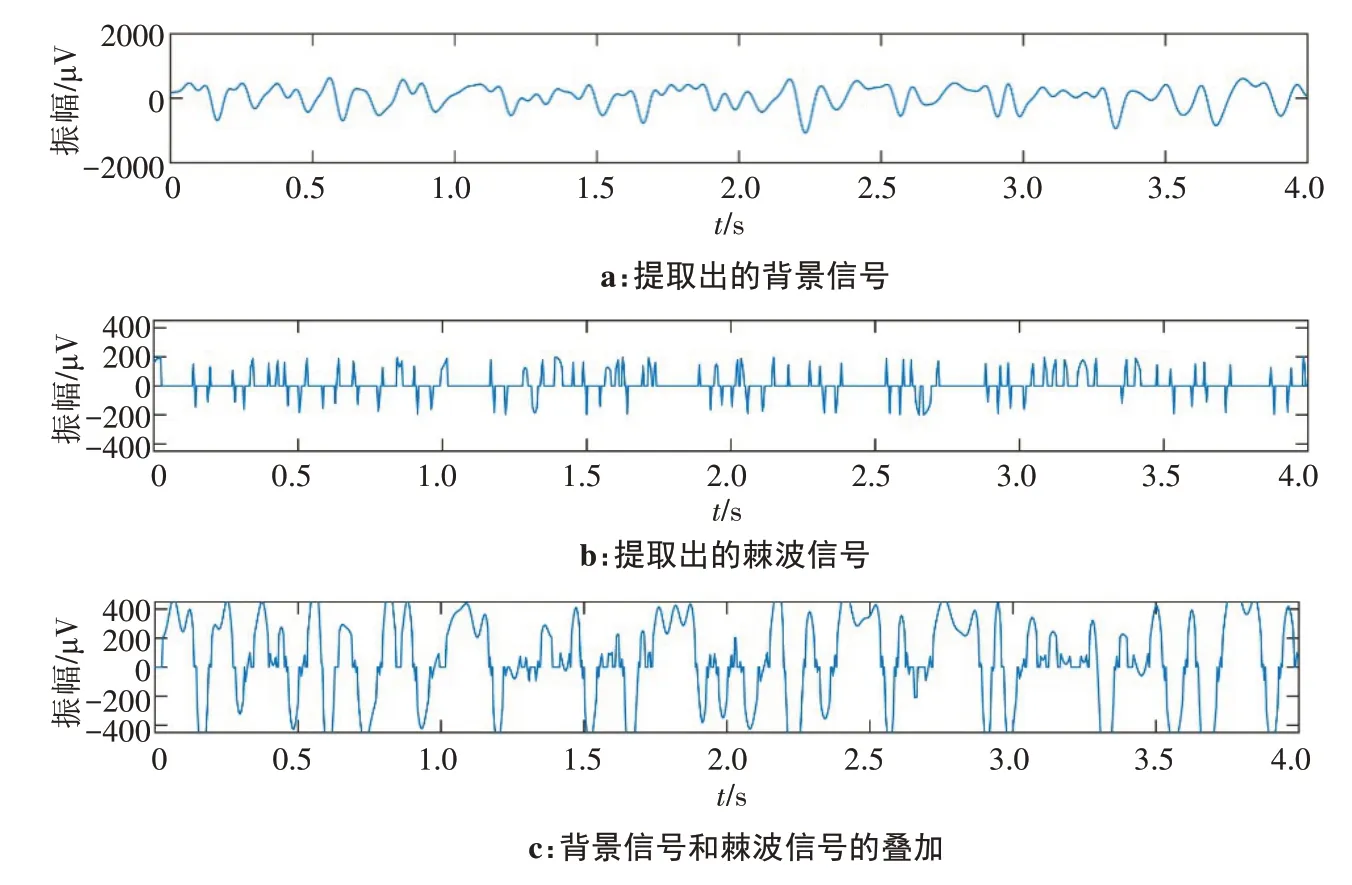
图8 癫痫患者a发作期节点（3,0）的脑电信号处理Fig.8 EEG signal processing of patient a in node(3,0)during epilepsy attack

图9 癫痫患者b发作期节点（3,0）的脑电信号处理Fig.9 EEG signal processing of patient b in node(3,0)during epilepsy attack

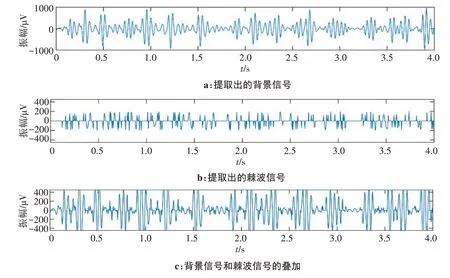
图10 癫痫患者a发作期节点（3,1）的脑电信号处理Fig.10 EEG signal processing of patient a in node(3,1)during epilepsy attack

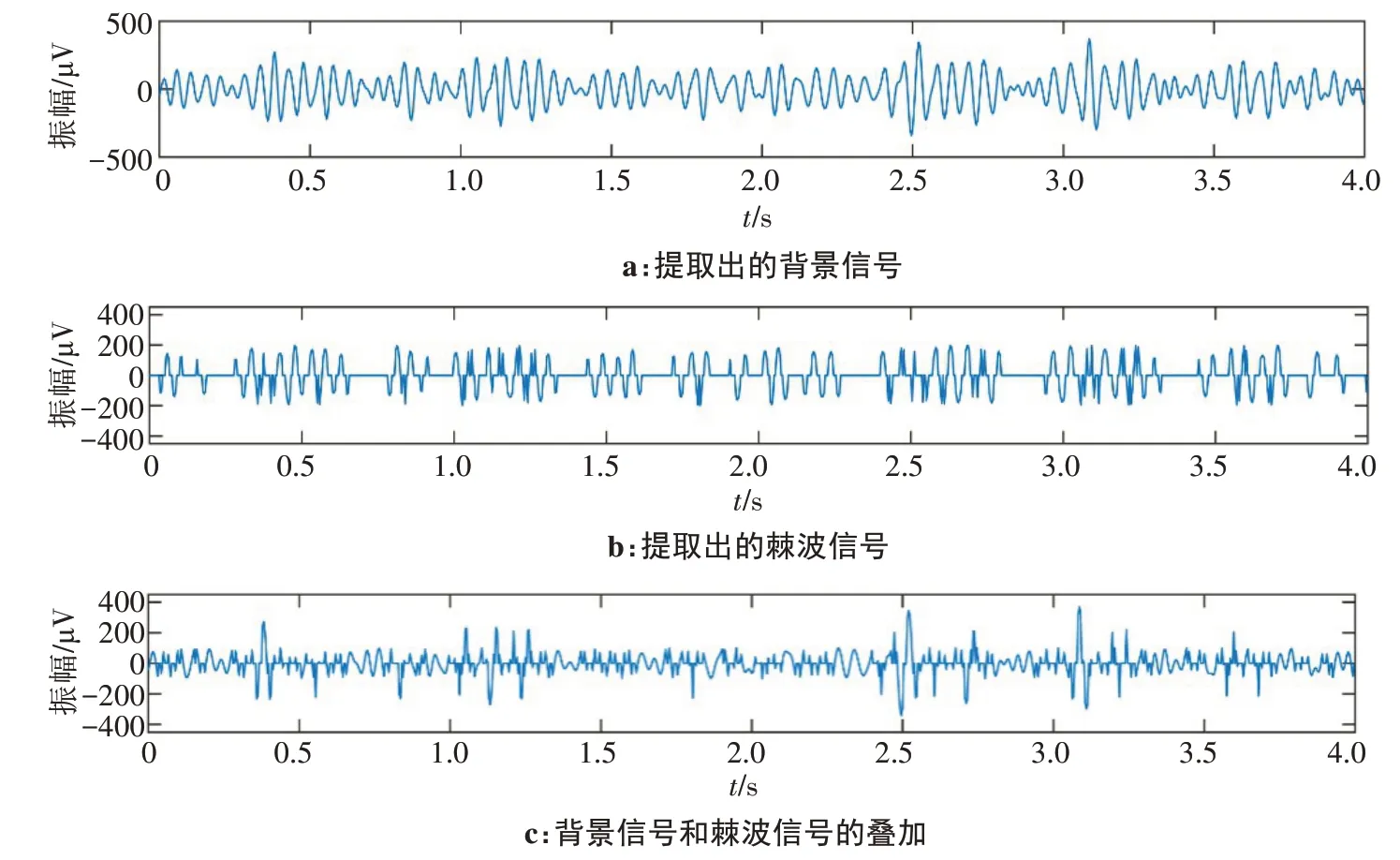
图11 癫痫患者b发作期节点（3,1）的脑电信号处理Fig.11 EEG signal processing of patient b in node(3，1)during epilepsy attack

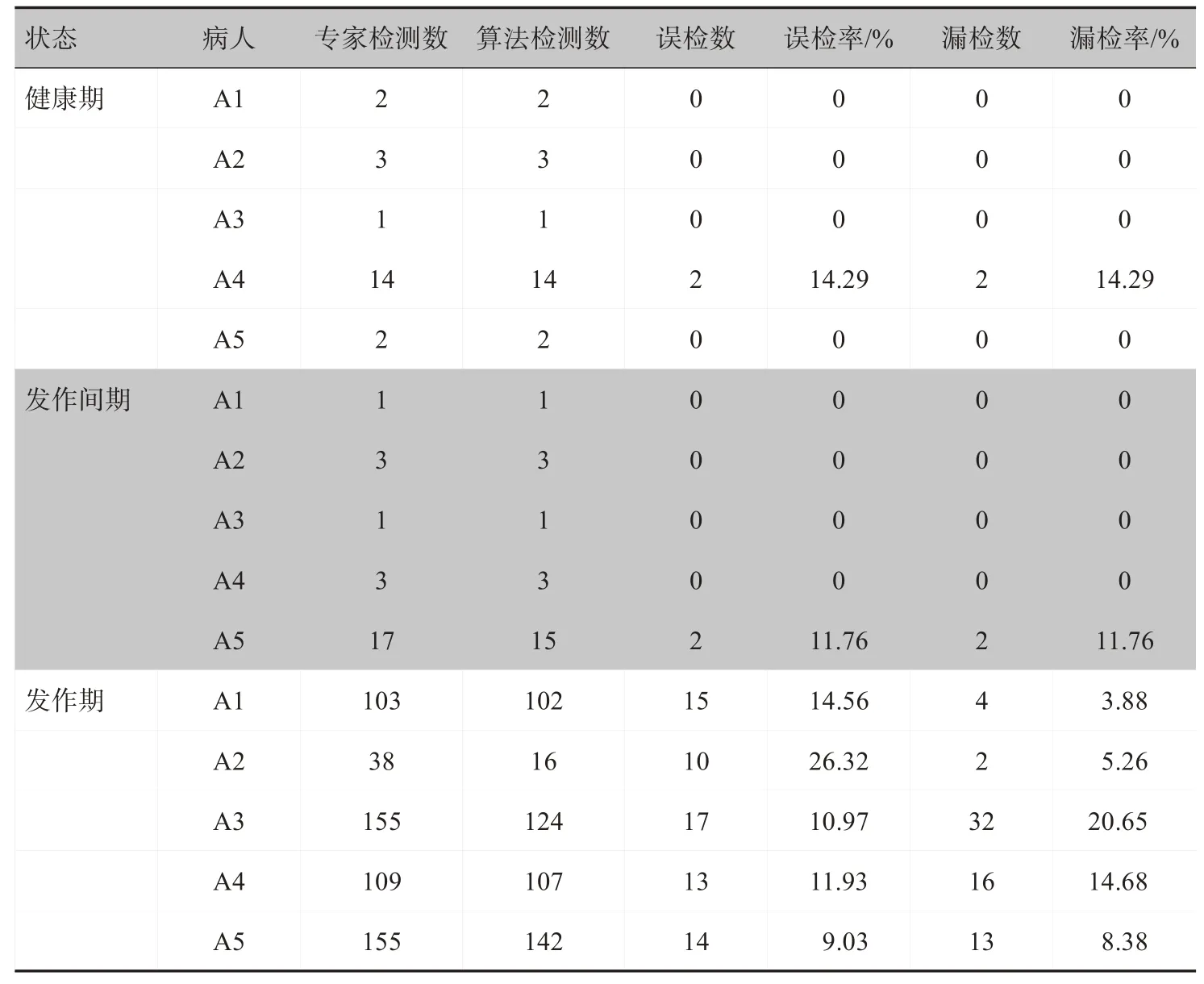
表3 5个癫痫患者在不同时期的棘波检测结果Tab.3 Results of spike detection in 5 epilepsy patients at different time

（3）基于小波包变换的棘波提取算法在癫痫患者健康期和癫痫发作间期的棘波提取准确率都在85%以上。癫痫患者发作期的平均误检率为14.56%（误检率=误检数/专家检测数，平均误检率为癫痫发作期误检率的平均值）；平均漏检率为10.57%（漏检率=漏检数/专家检测数，平均漏检率为癫痫发作期漏检率的平均值）。整体癫痫患者的棘波误检率为12.02%（总误检数/总专家检测数）；整体漏检率为11.70%（总漏检数/总专家检测数）。癫痫病人发作期棘波的误检率、漏检率差别比较大是因为有的棘波数据在脑电图上不是很明显，在人为检测时会造成一定程度的误检、漏检，而且选取的棘波物理特征不全面，例如没有考虑棘波的脉宽这一特性也使得该算法会造成一定程度的漏检和误检。

3 结论

本文提出的基于小波包变换结合棘波的频率、幅度等物理特性提取棘波的算法，能够提取出癫痫病人发作期脑电信号里大部分棘波。仿真结果得出该算法具有很低的漏检率和误检率（分别为12.02%和11.70%）。分析得出的结论与参考文献［14］的相关结论吻合。该算法可以为医生判断癫痫是否发作，进而确定癫痫的病灶提供了参考。