基于半张量积的修正压缩感知模型重构算法研究

刘俊梅， 马永刚

（榆林学院数学与统计学院，陕西榆林 719000）

2006 年，Donoho，Candès和Tao等提出压缩感知（Compressed Sensing，CS）［1-3］理论，该理论是一种充分利用信号的稀疏性和可压缩性对信号进行获取和重构的全新理论，一经提出就引起国内外相关研究人员的高度关注和重视，并迅速成为研究热点. 随着理论研究的深入，压缩感知在实际应用中也面临着许多有待解决的问题，如大尺寸图像信号压缩采样以及重构图像信号的应用研究一直存在待改善的问题. 压缩感知理论基于信号的稀疏性、观测矩阵的随机性以及非线性优化算法对信号进行采样和重构，然而在实际应用中，随机观测矩阵（如Gaussian，Bernoulli 等矩阵）要占用大量的存储空间和内存空间，存在实际应用困难等问题.特别是在信号优化重构过程中，当图像尺寸增大时，所需观测矩阵的存储空间也随之增大，造成重构算法内存消耗量成倍增加，这样很大程度上限制了压缩感知理论的实际应用.

因此，研究如何降低压缩感知过程中的观测矩阵、稀疏化矩阵的存储空间，并通过采用高效的信号重构算法，进一步提升压缩感知理论的应用仍然具有重要的理论价值和现实意义.

迄今为止，国内外不少学者提出相应的方法来解决压缩感知过程中观测矩阵占用内存多，消耗量大，重构算法计算复杂度高，不能适用于大规模实际应用等问题.

在文献［4-5］的基础上，本文将半张量积压缩感知模型采用正交匹配追踪算法进行信号重构，利用1 维可稀疏化信号对本文算法的重构性能进行验证和比较. 实验结果表明，采用本文所述拟合重构方法同样实现了对稀疏信号的重构.

1 半张量积理论［6］

2）结合律

2 压缩感知模型［7］

压缩感知模型简单描述如下：设向量组ψ=[φ1,φ2,…,φN]为空间RN中的一组正交向量基，信号x ∈RN在正交矩阵下ψ 能够表示为

式中：正交矩阵ψ 满足ψψT=ψTψ=I，α 为信号向量x 的系数向量，且αi=＜x，φi＞=φiTx.

若向量α 中非零项的个数K ≪M，则称信号x 或系数向量α 是稀疏的（K-稀疏的），式（6）为信号x 的稀疏化表示，压缩感知理论成立的大前提是待压缩信号本身是稀疏的或者可在某个空间域稀疏表示.

利用矩阵ΦM×N（与稀疏化矩阵ψ 不相干，其中M ≪N）作为压缩感知模型的观测矩阵，对信号x 进行压缩，该压缩感知模型可简单表示为

y 为压缩后的数据，称为观测向量. 通过这些少量的数据信号、系数向量α 的稀疏等约束条件，利用一些优化算法可以重构信号x .

从压缩感知模型中可知，观测矩阵参与了信号压缩观测、信号恢复这两个数据处理的重要环节，因此设计一个好的观测矩阵是压缩感知的核心问题，也很有研究的必要.

3 基于半张量积的修正压缩感知模型

为了降低观测矩阵在信号压缩、重构过程中的存储空间，本文采用半张量积理论重新构造观测矩阵［8-10］，即半张量积压缩感知模型定义如下：

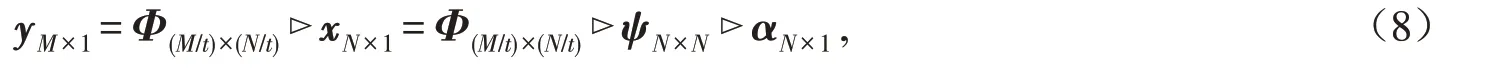
其中：Φ(M/t)×(N/t)是经过降维以后的随机观测矩阵，其中M/t，N/t，t 为正整数，且t ＜M，从以上模型可知，在相同数据的情况下，采用（8）式观测矩阵的存储空间是式（7）观测矩阵存储空间的1 t2倍.

利用半张量积的性质结合律，我们可以验证，式（8）是满足式（7）所示模型的，同样利用M 个观测值可以对N 维信号进行表示，即

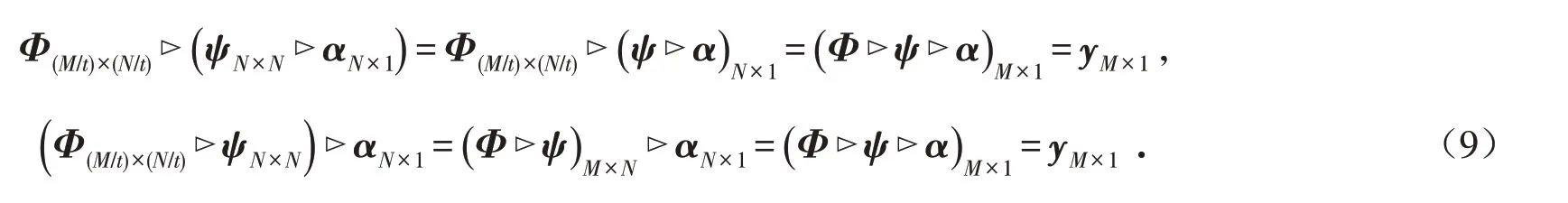
至此，本文所述问题的关键技术在于，如何采用式（8）所示的模型对N 维信号x 进行恢复或重构. 当t=1 时，观测矩阵维数为M×N，（8）式可表示成（7）式，由此可知，本文提到的基于半张量积的修正压缩感知模型是适用于式（7）所示的压缩感知模型的，为此，借鉴正交匹配追踪算法来讨论上述基于半张量积的修正压缩感知模型的重构方法.

4 基于半张量积压缩感知模型的正交匹配追踪重构算法

正交匹配追踪算法（OMP）［11-14］的基本思想：从字典矩阵A，注意这里字典原子是相互正交的向量，选择一个与信号y 最匹配的原子，构建一个稀疏逼近信号，并求出信号残差，然后继续选择与信号残差最匹配的原子，反复迭代，信号y 可以由最后的残差值与这些原子的线性组合之和表示. 很显然，如果残差值在允许的范围内可以忽略，则信号y 可表示为这些原子的线性组合，这里残差与已经选择过的原子正交的. 这就要求一个原子不会被选择两次，结果会在有限步达到收敛.

正交匹配追踪重构算法的流程如下.

输入：观测矩阵y，传感矩阵A=Φ(M/t)×(N/t)⊳ψN×N，信号稀疏度k；

输出：信号稀疏系数向量s，残差rt=y-A ⊳st.

5 实验结果

为验证本文算法迭代收敛速度、恢复稀疏解的能力，设计了两组实验进行验证算法的性能，第一组选择时域一维稀疏信号进行重构，并从不同稀疏度情况下时域一维稀疏信号的恢复误差、重构效果、重构时间等角度进行比较. 第二组选择变换域一维稀疏信号进行重构，同样从恢复误差、重构效果、重构时间等角度进行比较. 实验平台配置Intel（R）Core（TM）i7-8550U CPU，1.99 GHz主频，8 GB内存，64位Windows10操作系统，仿真采用软件Matlab 2014a.

5.1 时域一维稀疏信号压缩感知

设一维稀疏x 的稀疏度为k，且非零元素的位置随机，这里设置k 的最大值为M 2，因为文献［15］指出一个稀疏信号能够唯一恢复的前提是稀疏度最多不超过极限值M 2 .

为验证本文算法的重构性能，这里设定M=100，N=256，K=25，t=2，迭代次数设置为25 次，观测矩阵Φ(M/t)×(N/t)为满足N( 0,1/(M/t) )高斯独立分布的( M/t )×( N/t )维高斯随机矩阵，由于信号x 是稀疏的，所以稀疏化矩阵ψ 取为N×N 维单位矩阵，图1给出稀疏信号x 的原始信号、重构信号比较图. 实验结果显示，信号重构相对误差0.004，重构时间9.203，重构效果良好，值得推广应用.

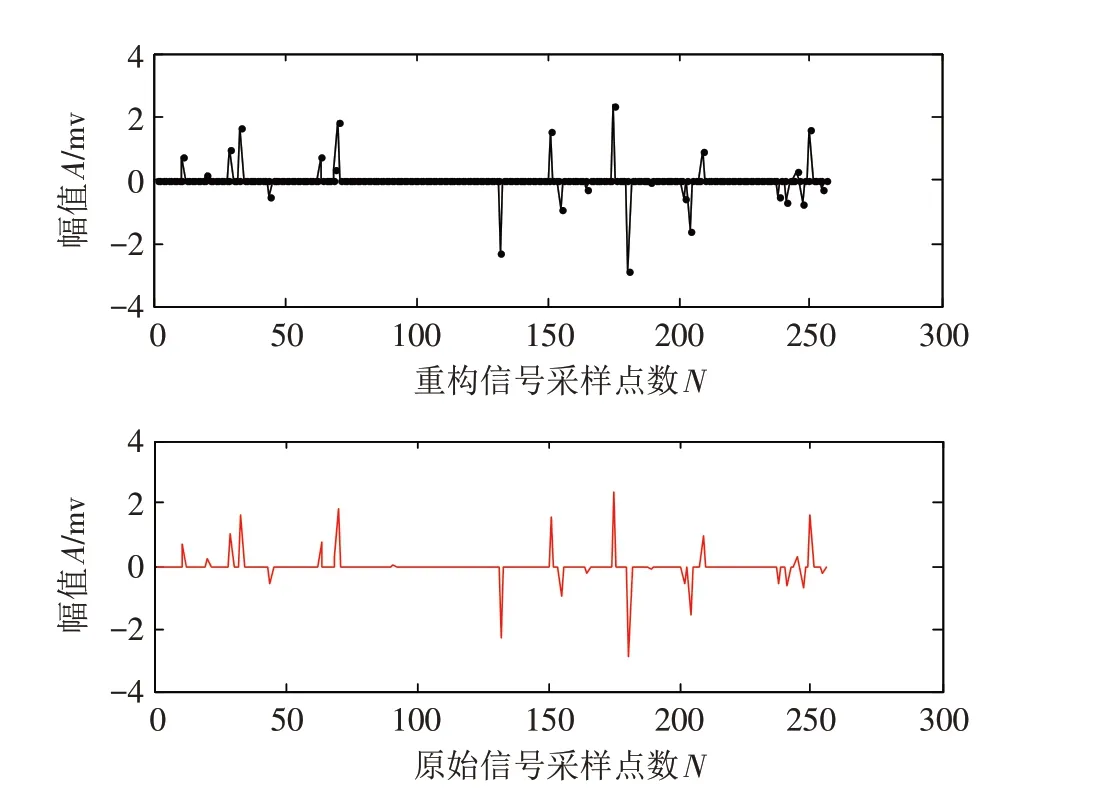
图1 时域稀疏信号的压缩感知重构过程Fig.1 CS reconstruction of time-domain sparse signals

5.2 变换域一维稀疏信号压缩感知

这里取M=100，N=256，t=2，迭代次数设置为25 次，观测矩阵Φ(M/t)×(N/t)为满足N( 0,1/(M/t))高斯独立分布的( M/t )×( N/t )维高斯随机矩阵，由于信号x 是变换域稀疏的，这里在压缩感知过程中选取的变换域ψ 为离散傅里叶变换域，x 在ψ下的稀疏度为4，图2给出变换域稀疏信号x 的原始信号、重构信号比较图. 实验结果显示，信号重构相对误差0.005，重构时间10.445，重构效果良好，值得推广应用.

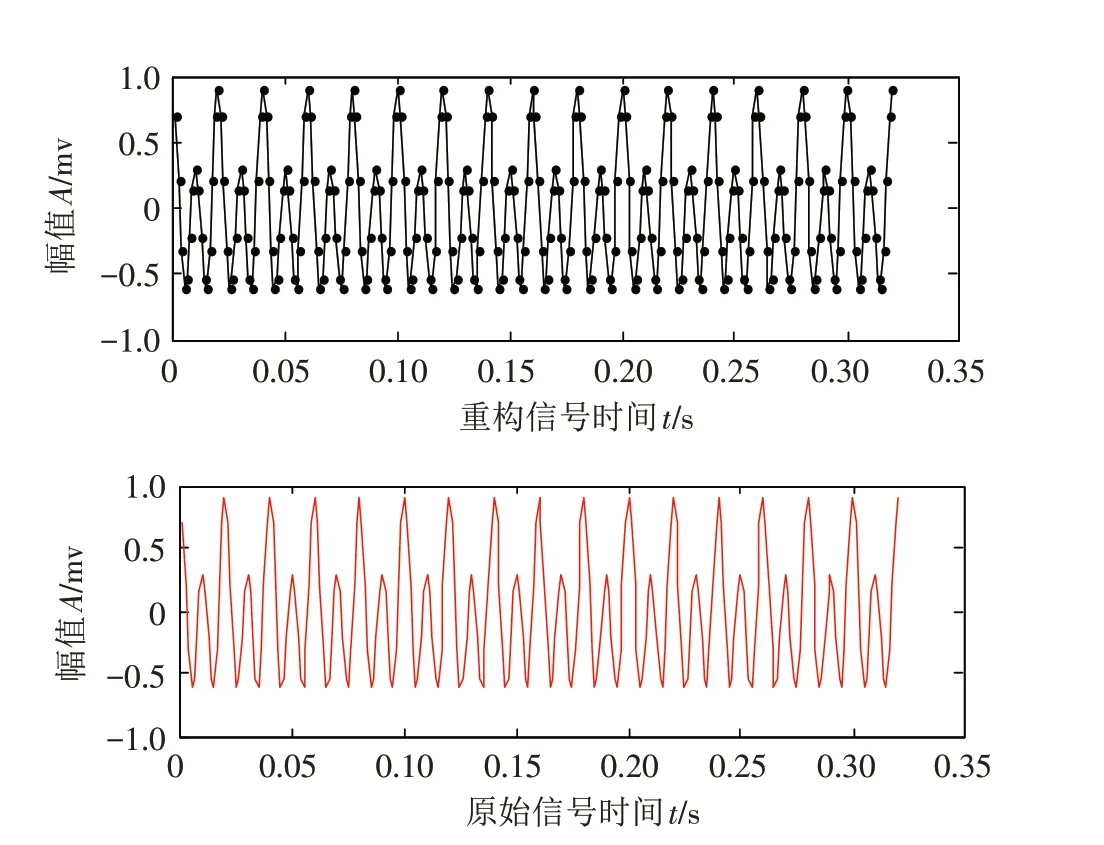
图2 变换域稀疏信号的压缩感知重构过程Fig.2 CS reconstruction of transformation domain sparse signals

6 总结与展望

本文利用半张量积理论知识，修正压缩感知模型，给出一种基于半张量积的修正压缩感知模型正交匹配追踪算法，通过一维稀疏信号的重构实验，表明该算法的重构效果良好，而且利用半张量积理论知识，减少了观测矩阵的存储空间，提高了重构效率，今后的研究中，考虑将该重构算法应用到二维稀疏信号的重构.