射影几何调和点列作图与阿波罗尼斯圆的联系
赵临龙
(安康学院数学与统计学院,陕西安康 725000)
1 问题背景
在射影几何中,调和点列是最基本也是最重要的概念,是射影几何理论建立及其研究的重要工具. 如利用调和点列形成的极点与极线概念,是研究二次曲线内在结构的重要工具. 因此,调和点列的几何作图成为人们讨论的热点.
在《高等几何》[1]中,关于调和点列的几何作图,先后给出欧式几何的圆中作图、仿射几何的平行线作图、射影几何的完全四边形作图和射影对应作图等.
现对于仿射几何的平行线作图进行讨论.
命题1 如图1. 已知点列A、B、C,求其调和点列D 满足(AB,CD)=-1.
作法 如图1. 在直线AB异侧过点C作直线A′B′,使A′C=CB′;连接AA′×BB′=S;过点S 作SD//A′B′交直线AB 于点D. 则点D为所求点,即(AB,CD)=-1.


图1 调和点列的作图Fig.1 Mapping of harmonic points

方程(3)的几何意义是以CD为直径的圆,该圆在欧式几何中叫作阿波罗尼斯圆.
命题2[2](阿波罗尼斯圆)已知两点A、B,C、D分别为线段AB的定比λ(λ≠1)的内外分点,则以CD为直径的圆上任意点到A、B两点的距离之比为λ.
2 问题讨论
阿波罗尼斯(Apolloning,约公元前260—170)是古希腊著名的数学家,与欧几里得、阿基米德一起被称为亚历山大时期的数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要的研究成果集中在他的代表作《圆锥曲线》一书中,阿波罗尼斯圆是他的研究成果之一[2].

推论3 已知两点A、B,C、D 分别为线段AB 的定比λ(λ≠1)的内外分点,且交点S=AA′×BB′,则点S 在阿波罗尼斯圆上的充分必要条件是AA′∶BB′=λ.
此时,当直线AS 为阿波罗尼斯圆的切线(S 为切点)时,则由圆直径的对称性,得到该阿波罗尼斯圆的切线AS′(S′为切点),于是SS′是极点A 关于该阿波罗尼斯圆的极线,则该阿波罗尼斯圆心与极点的连线AB⊥SS′[3].
推论4 如图2,已知两点A、B,C、D分别为线段AB的定比λ(λ≠1)的内外分点,关于阿波罗尼斯圆过点B 作垂直于直径的弦SS′,则AS、AS′为该圆的切线.
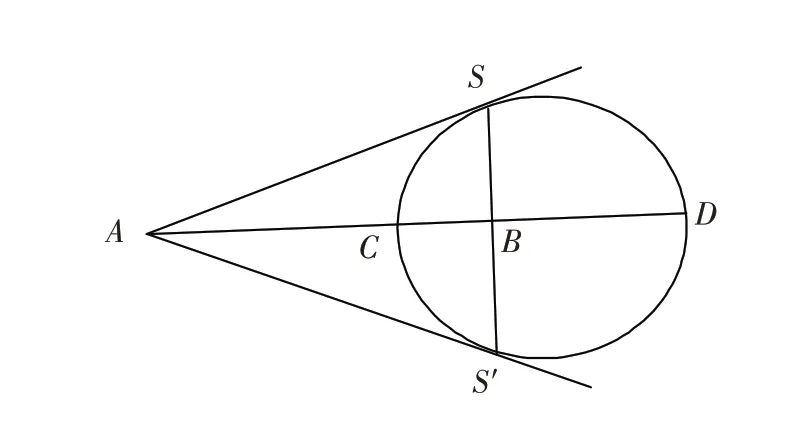
图2 阿波罗尼斯圆的切线作图Fig.2 The tangents of Apolloning circle
3 理论应用
3.1 几何作图题
例1 已知两点A、B,C、D分别为线段AB的定比λ(λ>1)的内外分点,作出阿波罗尼斯圆.
作法1 对于线段AB,直接作出其定比为λ(λ>1)的内外分点C、D,则以CD 为直径即可作出阿波罗尼斯圆.
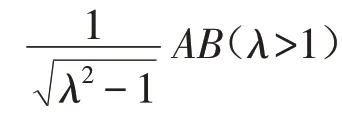
证明 如图2,设AB=2a,则

得到以CD为直径的阿波罗尼斯圆.
推论5 对于(AB,CD)=-1,过阿波罗尼斯圆外点A作该圆的切线AS(S为切点),则切点S与该圆直径直线ACD构成的直线SC,SD分别为∠ASB的内、外角平分线.
注 在例1中,对于0<λ<1,只需将点A、B位置互换即可. 另外,作法2较作法1麻烦,但正是利用了调和点列性质,充分反映了事物的本质.
例2 已知点P及圆O,作过点P关于该圆O的切线.
①当点P为圆O上点S.
作法 如图2,过点S作SS′垂直圆O的直径CD于B,作出点列D、C、B的调和点A,连接AS,则AS为已知圆O的切线.
证明 如图2,由于(AB,CD)=-1,且CD 为直径的圆O为阿波罗尼斯圆. 此时,SS′⊥CD=B,由推论3,得到AS为已知圆O的切线.
②当点P为圆O外点A.
作法 如图2,作出点列A、D、C 调和点B,过点B 作与圆O 直径CD 垂直的弦SS′,连接AS、AS′,则AS、AS为已知圆O的切线.
证明 如图2,由于(AB,CD)=-1,且直径为CD 的圆O 为阿波罗尼斯圆. 此时,SS′⊥CD=B,由推论3,则AS、AS′为已知圆O的切线.
注 在例2 中,其做法较一般的欧式几何作法麻烦,但利用调和点列将两种作法统一起来,充分揭示其内在联系,这正是数学研究所追求的.

图3 竞赛题图示Fig.3 Chart of contest question
3.2 问题答题
由于阿波罗尼斯圆的趣味性,它成为研究相关问题的重要方法,尤其在相关高考题研究中,文献不少[4-21].
例3(2001年中国西部数学奥林匹克题) 如图3,过圆O 外一点A 作其切线AS、AT,OA 与圆O 和ST 分别交于点C、B,EF为过B的任意弦. 求证:C为ΔAEF的内心.
证明 如图3,由于阿波罗尼斯圆上任意点E到线段AB 两端点满足EA∶EB=λ=AC∶CB,则EC 为ΔEAB 的内角平分线;同理FC 为ΔFAB 的内角平分线,即点C 为ΔAEF的内心.
推论6 如图3,在阿波罗尼斯圆中,对于(AB,CD)=-1,过点B作不与CD重合的弦EF,则AB平分∠EAF.

图4 高考题图示Fig.4 Chart of the University Entrance Examination question
推论7 如图3,在阿波罗尼斯圆中,对于(AB,CD)=-1,过点B作不与CD重合的弦EF,则点C、D分别是ΔAEF的内心和外心.
例4(2019年江苏省高考数学专题应用题) 如图4,一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8 n mile的A处,发现在其北偏东30°方向相距4 n mile的B处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍. 假设缉私艇和走私船均按直线方向以最大航速航行.
1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;
2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截,并说明理由.
解法 1)略.
2)如图4. 建立平面直角坐标系,则A(0,0),B(2,2 3),设缉私艇在P(x,y)处成功拦截到走私船,因为缉私艇的最大航速是走私船最大航速的3倍,即PA∶PB=3.



