高新技术开发区关联性的空间计量分析

王宝英， 张 可， 王玮琦

（中北大学经济与管理学院，太原 030051）

十八大以来，我国提出要将创新驱动作为引领发展的第一动力，以知识积累、技术进步、劳动要素提升推动发展方式的转变，开辟新的发展空间. 高新技术开发区作为中国经济发展的新政策，承担了提升经济发展的重要使命，经过30年的发展，新一批达到国家规模和省规模的开发区也在国内快速建成，一部分发展了在此区域内的企业的整体创新性，另一部分也积极地影响了附近区域的经济增长. 但是，由于不同地区在资源、经济基础以及创新水平上的差异，其开发区的发展也各不相同. 那么，开发区的发展是否只受到本地区相关政策的影响，发展较好的开发区是否其周围开发区也有较好的经济绩效，而发展缓慢的开发区其邻近开发区是否呈现出缓慢发展状态.

19世纪80年代开始，我国逐渐开始建立开发区，截至2018年，共计156个国家级高新开发区，位于东部的有67个，中部有37个，西部开发区有36个，东北区域有16个. 通过对文献中关于开发区选址影响因素研究发现，开发区在选址上的决定因素主要有区位条件、经济基础、政策影响. 从时间上看，东部开发区建设速度和发展始终领先于其他地区. 从区域角度看，国家开发区数量最多的4 个省份分别是江苏（17 个）、山东（13个）、广东（12个）、湖北（9个），开发区在地区上的集聚是否只受到这3个因素的影响，有相似的报告指出开发区的整合对周边地区的经济增长有着积极的势头. 那么，不同开发区之间是否在空间上产生相互影响、相互制约、相互作用. 鉴于此，从空间维度来探究不同开发区溢出效应以及相互之间影响程度如何.

1 文献回顾

目前对高新技术开发区的关注已成为研究我国区域经济的一个热点问题，国内现有文献通过定性和定量分析对高新技术开发区发展进行研究. 国内高新技术产业发展的定量研究体现在效益的测量、开发区将城市空间体系的影响和经济区域空间的生产整合上. 蔡善柱等［1］分析计算了国内众多开发区的整体经济效益和主要的因素生产效率，得出TFP从东到西依次递减的结论；刘满凤等［2］运用三阶段DEA 模型得出了类似的结论，还指出中部和西北地区开发区域的改革速率降低原因是环境的影响. 这些文献仅针对开发区自身发展进行了研究，随着研究的深入，一些学者开始考虑开发区在空间上的影响. 张晓平等［3］研究了经济开发区域对空间体系的影响；王慧［4］把开发区的发展规划分成了四个主要部分研究了开发区的各个部分对空间体系的探讨；郑江淮等［5］在空间维度上以开发区的产业集聚作为研究对象；吕卫国等［6］研究了制造业企业在空间上的区位选择，有关的分析指出空间体系的制约对开发区的发展是很深的，不过单单是对一个区域空间上开始研究；李圣宏［7］增加了分析区域的规模，收集了众多空间单位对开发区的改革技术发展的关联性进行分析.

对于我国高新技术开发区定性分析主要通过探究开发区的发展模式、创新体制、综合评价和政策建议等几个方面展开. 一些学者认为早期我国高新技术开发区面临的一些问题主要是行政管理的不规范［8-9］，而现阶段面临的主要问题是发展模式的问题. 吴中兵等［10］提出开发区发展重心向创新和转型升级转变，产业园的聚集成长模式则变成这一改革的转折点. 对于开发区的综合评价主要包括土地集约利用评价［11］、开发区发展水平综合评价［12］、产城融合度评价［13］以及开发区绩效评价［14］. 冯燕妮等［15］以山西省为例子，融合了山西地区的经济发展现状，模仿了国内众多地区的成功案例，发表了山西开发区经济发展的主要政策. 国外学者则注重于以开发区作为载体以解决地区就业问题［16-17］和税收政策问题［18］. Neumark&Kolko［19］以新的层级数据和地理测绘方法对加利福尼亚州的开发区进行分析，结果表明开发区不增加就业，在开发区的政策激励下就业没有向低工资工人转移. Elvery［20］对加州和佛罗里达州开发区的研究得出类似的结论. Freedman［21］研究表明开发区项目对德克萨斯州居民就业产生了正向作用. 1997年法国实施了EZ计划，Pauline等［22］研究认为短期内法国的EZ计划在持续的财政支持下实现了就业的稳定，吸引企业到贫困地区.

从上述分析来看，现有文献大多从一个空间单元对开发区进行分析，从多个空间单元研究高新技术开发区空间关联性文献较少. 然而，Fridemann［23］提出的核心边缘扩散理论认为，所有区域基本都是中心主要地区和周边各地区聚集而成，中心区域对于周边区域的辐射将周边区域在经济增长的时候演变成了新的中心地区，进一步地向外围扩散. 因此，本研究选取多个高新技术开发区空间单元，采用各项指标的年平均增长率，以克服截面回归数据无法反映一个时段动态信息的缺陷，建立了反距离空间的比重阵列，把探索性的空间数据研究和空间计量模型对高新技术开发区的地域上的有关性进行了深入的研究，提出促进高新技术开发区在空间单元上合作交流的政策建议.

2 数据说明与模型选择

2.1 空间加权矩阵的设定说明

为了分析各个高新技术开发区域在地域上的相关性，要使用空间计算模型进行研究，两种基本模型如下：

空间滞后模型

空间误差模型：

式中：β 是自变量的弹性系数；ρ是空间回归系数；w是空间权重矩阵；ρ是空间误差自相关系数；u是随机误差项. 以本文的54个开发区为例，w空间权重矩阵表示为：

空间权重矩阵的构建有以下几种：一是用地区间地理位置上的有关性进行确定；二是按照区域空间上所在的位置坐标来分析两地区的距离，使用距离数据的倒数或距离的二次方的倒数来计算；第三，将引力模型引入空间权重矩阵，以两地某种观测量的乘积除以其距离来反映两个区域的空间关联强度.

认识到由于开发区间不一定有地理位置的衔接部分，因此使用相邻关系来建立比重的矩阵是不正确的，要是用引力的模型来建设空间比重矩阵，由于尚不能够清楚地知道开发区之间是以何种方式产生空间联系，不能够确切地衡量是哪一种要素在开发区之间流动，所以用相邻的两个开发区间距离倒数的二次方来构建矩阵.

2.2 模型设定

开发区的经济活动本质上仍是投入产出的过程，开发区的发展需要投入大量人力、物力和财力，同时将技术创新和开发区内企业数作为影响因素，分析影响开发区经济发展的主要因素，构建传统计量模型：

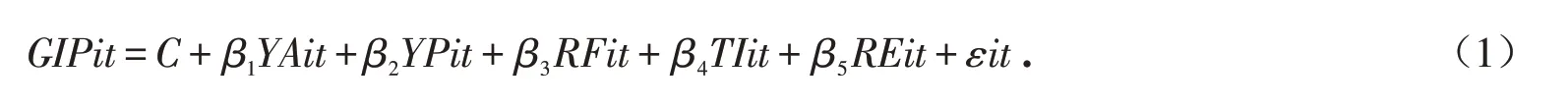
指标选取根据参考文献以及本文研究需要所建立，研发产出以各个开发区工业总产值GIP衡量. 式（1）中：YA代表各个开发区年末资产；YP代表年末从业人员数；RF代表财力投入以科技经费衡量；RE代表开发区内企业个数；TI代表技术创新以技术收入衡量；C为不随时间变化的截距项；i代表高新技术开发区编号；t为对应的研究年份；ε 为随机误差向量；β 为参数反映自变量对因变量影响.

为了分析54个高新技术开发区的空间关联性，在传统的计量模型中引入空间滞后变量作为内生变量，得到如下模型：

1）空间滞后模型

式中：ρWGIPit为空间滞后变量，表示其他开发区对开发区自身的影响；ρ为空间滞后系数，反映了其他开发区对开发区自身的影响程度；W为空间权重矩阵.

2）空间误差模型

式中：Wuit表示空间之间的相关性并不一定表现在开发区与开发区之间的工业总产值上，同样有可能体现在哪些不能测量的变量上，λ体现了两区域在空间上的影响比重.

2.3 数据说明

分析数据来源于《中国火炬统计年鉴》（2010—2017），《中国开发区审核目录公告》（2018）考虑到数据的可得性以及开发区建立的时间，选取截至2010年的56个国家级开发区，由于乌鲁木齐开发区、兰州开发区与其他开发区距离较远，避免造成误差从中去除选择54个开发区. 由于存在空间差异，传统的时间序列模型回归方法会遇到相关性、异方差的问题，以截面数据分析又无法反映不同时期的动态信息，为了克服这一缺陷，本文采用54个开发区各项指标2009—2016年平均增长率，既考虑了空间维度，也将时间维度引入进去，是一种较为可行的方法.

3 实证分析

3.1 空间自相关实证分析

3.1.1 全局空间自相关分析 测量空间自相关常用Moran’s I指数表达，值域为［-1，1］，以下是其表达式：

式中：N为开发区单元数；xi为开发区i的属性观测值，i=1，2，…，n；wij表示空间权重矩阵. 因为在地理位置上，各开发区直接不是相邻的，所以开发区的邻近关系按距离标准进行定义，空间权重矩阵元素以两开发区之间距离平方的倒数作为要素，两区域之间距离小的赋予较大的权重，距离大的赋予较小的权重. 以Moran’s I指数的大小对开发区空间关联性进行衡量，Moran’s I指数通常用Z统计量检验，表达式如下：

将开发区2009—2016年中的基本数值为属性观测值基础，高新技术开发区之间的距离作为构建空间权重矩阵的基础，计算得到2009—2016年以各开发区空间关联评价指标的全局Moran’s I指数，得到的结果如表1所示.

表1 各指标Moran's I指数Tab.1 Moran’s I index of each indicator

运用geoDa计算得出2009—2016年间54个开发区GIP、科技经费内部支出、技术收入和年末从业人员的年均增长率Moran’s I指数. 结果显示，在5%的显著性水平下GIP、年末从业人员和科技经费内部支出空间自相关是显著的，技术收入增长率的空间自相关性不显著. 根据Z值的检验结果可以看出，GIP、科技经费内部支出和年末从业人员增长率呈现出显著的空间集聚特征，以下研究将以GIP、科技经费内部支出以及年末从业人员数设为研究变量. 图1～3分别为GIP、年末从业人员和科技经费内部支出的999次模拟结果，也说明开发区之间空间相关性的存在，分布呈现正态分布.

图1 GIP Moran's I 999次模拟结果Fig.1 Simulation results of GIP Moran’s I for 999 times

图2 年末从业人员Moran's I 999次模拟结果Fig.2 Simulation results of Moran’s I for the practitioners at the end of 999 times

图3 科技经费内部支出Moran's I 999次模拟结果Fig.3 Simulation results of Moran’s I 999 times of internal expenditure of science and technology funds

3.1.2 局部空间自相关分析开发区的单元总数设为N，Yi为开发区i对应的属性观测值，空间权重矩阵用wij表示（i=1，2，…，n），Moran’s I指数表示其他高指标开发区包围某高值观测指标开发区，或低指标开发区包围低值观测指标开发区；Moran’s I指数表示某高值观测指标开发区被其他低值指标开发区包围，或低值观测指标开发区被高值指标开发区包围.

3.1.2.1 Moran’s I散点图 Moran’s I散点图可以明确表示开发区属于什么集聚类型，横坐标表示对应描述变量，纵坐标表示空间滞后变量，以下将通过Moran’s I散点图对开发区的空间关联性进行研究.

1）GIP变量

图4中，位于第一象限（高高集聚类型）分别是贵阳、合肥、中山、佛山、济南、绵阳、厦门、湘潭、宝鸡、桂林、株洲、重庆、长沙、南昌、杨凌、西安、南宁、武汉、襄樊等19个高新技术开发区，表示GIP 增长率高的开发区被GIP 增长率高的开发区包围；位于第二象限（低高集聚类型）的分别是昆明、洛阳、成都、海南、福州、广州、深圳、珠海、石家庄、无锡等10 个高新技术开发区，表示GIP 增长率低的开发区被GIP 增长率高的开发区包围；位于第三象限（低低集聚类型）的分别是大连、鞍山、吉林、包头、威海、淄博、哈尔滨、太原、潍坊、苏州、南京、常州等12个高新技术开发区，表示GIP增长率低的开发区被GIP增长率低的开发区包围；位于第四象限（高低集聚类型）的分别是长春、大庆、青岛、天津、宁波、保定、北京、杭州、泰州、上海、惠州、郑州等12 个高新技术开发区，表示GIP 增长率高的开发区被GIP 增长率低的开发区包围.

2）年末从业人员变量

图5 中，位于第一象限（高高集聚类型）分别是郑州、北京、厦门、保定、襄樊、济南、杨凌、惠州、武汉、长沙、桂林、深圳、株洲、南昌、中山、佛山、南京、广州、泰州、潍坊、西安等18个高新技术开发区，表示年末人员增长率高的开发区被年末人员增长率高的开发区包围；位于第二象限（低高集聚类型）分别是杭州、苏州、海南、石家庄、洛阳、太原、昆明、常州、珠海、重庆、福州、湘潭、淄博、无锡等14个高新技术开发区，而其中年末人员增长率高的开发区包围增长率低的开发区；位于第三象限（低低集聚类型）分别是绵阳、大庆、大连、沈阳、哈尔滨、包头、吉林、鞍山等8个高新技术开发区，同上相反，年末人员增长率低的开发区包围增长率高的开发区；位于第四象限（高低集聚类型）分别是长春、威海、成都、青岛、宁波、合肥、贵阳、上海等8个高新技术开发区，与第三象限相同，由低包围高.

图4 GIP Moran's I散点图Fig.4 GIP Moran’s I scatter plot

3）科技经费内部支出变量

图6 中，位于第一象限（高高集聚类型）分别是贵阳、西安、杭州、长沙、株洲、合肥、重庆、广州、佛山、南昌、深圳、海南、珠海、惠州、武汉、杨凌、福州、厦门、南宁、襄樊等20 个高新技术开发区，表示科技经费变量增长率低的开发区包围增长率低的开发区；位于第二象限（低高集聚类型）的分别是苏州、南京、常州、无锡、泰州、桂林、洛阳、成都、中山、湘潭、宝鸡、昆明等12个高新技术开发区，其结论与第一象限相反；位于第三象限（低低集聚类型）分别是包头、沈阳、大连、鞍山、吉林、哈尔滨、太原、威海、青岛、潍坊、淄博、石家庄、绵阳等13个高新技术开发区，看出科技经费变量增长率高的开发区包围增长率低的开发区；位于第四象限（高低集聚类型）分别是宁波、保定、北京、天津、上海、济南、郑州、大庆、长春等9 个高新技术开发区，表示科技经费变量增长率低的开发区包围增长率高的开发区.

3.1.2.2 LISA集聚图和显著性统计图 LISA集聚图可以将变量呈现不同空间关系的开发区在地图上表示出来，与Moran’s I 散点图结果分析对照，对开发区之间的空间自相关关系补充说明，为了更加直观地了解开发区之间的关系，以开发区所在的地级市来呈现.

图5 年末从业人员Moran's I 散点图Fig.5 Moran’s I scatter diagram of practitioners at the end of the year

图6 科技经费内部支出Moran's I 散点图Fig.6 Moran’s I scatter diagram of internal expenditure of science and technology funds

图7 GIP变量LISA集聚图与LISA显著性统计图Fig.7 LISA cluster diagram and LISA significance statistical diagram of GIP variable

1）GIP变量

在5%的显著性水平下，襄樊、武汉、南昌、重庆、桂林、南宁、株洲、湘潭、长沙开发区GIP增长率呈现高-高集聚特征，吉林、沈阳、鞍山、大连、威海呈现低-低集聚特征，大庆和长春作为GIP增长率高的开发区被其他增长率低的开发区包围，昆明作为GIP增长率低的开发区呈现出低高集聚类型.

2）年末从业人员变量

以年末从业人员作为变量，在5%的显著性水平下，由图8可以了解到只有济南和襄樊两地出现高聚集特征，昆明、长春、襄樊、沈阳、吉林和大庆的集聚特征表现与GIP增长率变量类似.

图8 年末从业人员变量LISA集聚图与LISA显著性统计图Fig.8 LISA cluster diagram and LISA significance statistical diagram of practitioner variables at the end of the year

3）科技经费内部支出变量

由科技经费内部变量与人员变量的LISA集聚图与显著性检验图对比可知，大庆和长春作为增长率高的开发区被其他增长率低的开发区包围，沈阳、威海、大连、鞍山呈现低-低集聚状态，昆明开发区在三幅LISA集聚图中都表现出被其他高增长率的开发区包围.

图9 科技经费内部支出变量LISA集聚图与LISA显著性统计图Fig.9 LISA cluster diagram and LISA significance statistical diagram of the internal expenditure variables of science and technology funds

3.2 开发区空间扩散模型分析

3.2.1 模型分析 首先进行普通计量模型分析，从表中可以发现，以GIP年平均增长率作为被解释变量，F统计量为25.173 4，P值为0，回归方程基本成立. 在5%的显著性水平下，年末资产、年末从业人员和科技经费内部支出对开发区年平均增长率对GIP 年平均增长率具有正向影响，弹性系数分别为0.222 4、0.365 4 和0.327 3，由此可知提高三项投入能够获得相应的工业总产值提高. 而在影响层面企业数量年平均增长率对开发区发展并不是正向的，且没有达到10%的显著性水平，说明企业数量增长速度可能趋于饱和，增长速度过快反而会对GIP增长起到抑制作用. 技术收入的弹性系数明显低于10%的标准水平，其主要原因是各开发区主要产业各不相同，并不是所有的开发区都以技术创新来提升工业产值. 从普通计量模型回归结果来看，要加快工业生产总值的增长速度，还是要加大人力资源、科技资金的投入.

其次进行空间滞后模型分析，在5%的显著性水平下，GIP空间滞后项的弹性系数为0.219 8，说明一定区域范围邻近开发区的发展对本开发区的发展存在较强的积极影响，高新技术开发区的发展具有空间关联性. 年末资产、年末从业人员和科技经费内部支出变量的弹性系数分别为0.197 3、0.386 6、0.308 6对开发区自身发展均存在正向影响，企业数量与技术收入变量的弹性系数较小且二者均不显著. 这个结果与普通计量模型基本一致，从模型结果上看，加大人力资源以及资金的投入，提高其增长率，促进开发区之间的相互交流才能提高开发区的生产效率.

最后进行空间误差模型分析，由表2可以看出，在5%的显著性水平下，λ=0.320 6，P值为0.060 5，表明高新技术开发区空间关联性的存在且相互之间影响程度为正，其余所有变量的弹性系数与P值大小基本与传统计量模型和空间滞后模型分析相同.

表2 模型估计结果Tab.2 Model estimation results

3.2.2 模型检验 从上述的分析来看，普通计量模型、空间滞后模型与空间误差模型都得出类似的结果，为了确定哪一种模型对开发区之间空间关联性的分析更为准确，本文根据Paul Elhorst提出的判断模型适用条件进行选择，根据LM-lag、LM-error、Robust LM-lag和Robust LM-error显著性进行检验. 检验统计量如下：

根据LM检验结果，空间滞后模型LM检验值为4.625 2，Robust-LM检验值为2.761 7，显著性检验都达到理想值，空间误差模型LM-lag检验值和Robust LM-lag检验值对应的P值均没有达到10%的显著性检验. 因此，空间滞后模型是最佳模型. 检验结果如表3所示.

表3 LM检验结果Tab.3 LM test results

4 对策与建议

破除开发区发展的距离障碍. 距离障碍主要包括空间距离和历史文化距离，从研究结果看，开发区的发展具有空间关联性，超出一定的距离门槛，很大程度上阻碍了开发区之间的交流，但是距离太近，也有可能使开发区之间存在相互影响而失去各自的发展特点. 开发区的空间距离一定程度上可以通过现代通信手段和改善区域交通来实现，但如果可以通过发达的互联网和物联网，搭建网络交流合作平台，可以大幅度降低空间距离产生的影响. 其次是历史文化距离，一些开发区由于受到固有的发展理念和发展方式的影响，其主导产业转型较慢，以太原和西安两个距离较近的高新技术开发区为例，太原开发区主导产业从煤化工向新能源转型，而西安开发区一直从事与高科技产业发展，导致两开发区之间产生较大发展差异，这与当地的历史文化环境是分不开的，所以当地政府要积极引导地区的发展理念，改善开发区之间空间距离的同时，尽可能的拉近开发区之间的历史文化距离.

破除开发区发展的交流障碍. 开发区之间的交流发展要消耗时间、精力、财力. 对于处于优势的开发区来说，短期内见不到收益，意味着其知识技术所有权，优势地位的丧失；而处于劣势的开发区由于风险因素而不具有向优势开发区靠近的动机，就会导致在交流层面上开发区之间无法准确沟通，这便需要政府出面调解，提高更加优惠的政策给优势开发区，为劣势方提供相应的激励机制. 相近的开发区之间具有更高的吸引力，政府应当拉近相似开发区之间的距离，倡导具有相近发展环境，相似主导产业的开发区之间加强交流.

实现跨区域协同发展. 由于地理位置的影响，使得不同区域开发区的经济发展水平存在较大影响. 从研究的54个开发区来看，东部由于人力、财力、地理位置和发展历史方面的优势发展较快，中西部部分开发区则受到历史条件和社会环境的制约发展滞后. 从研究结果来看，人力资源快速增长相比财力投入和科技经费投入的增长对开发区的经济发展有着更重要影响，进一步说，大多数开发区的主导产业是高新技术产业，科技人才决定了开发区未来的发展方向与产出绩效，一些落后开发区的人才流失现象确实不可避免. 但如果可以通过提高科技人员的工资待遇、发展空间以及工作条件等，可以减缓人才的流失，实现人才回流.对于优势区域的，还需要通过政府作为抓手，采取一定激励机制，通过科技人才在区域间的流动实现开发区跨区域协同发展.