浮筒式单点系泊系统的设计

王秋玲,甘泉峰,朱月强

(阜阳师范大学 物理与电子工程学院,安徽 阜阳 236037)

0 引言

海洋是地球生命系统的一个重要组成部分,也是社会可持续发展的宝贵财富。进入21世纪,一场以开发海洋为标志的”蓝色革命”正在世界范围内兴起。系泊系统在海洋经济发展、环境保护、绿色能源开发、防灾减灾和国防安全等方面均具有广泛的应用。

单点系泊系统主要应用在海洋工程领域中单点系泊储油装置和缷油装置中,以及在海洋工程、海洋观测、海洋养殖等领域,利用单点系泊进行定位,其中浮筒式防风单点系泊系统作为单点系泊系统的一种形式,具有极广的自由度,系泊的船只可绕着单点做360° 旋转,能够根据潮汐或风、浪、流自动调整方位,使系统中各个组件作用在单点上的系泊力最小。它主要由锚碇、锚链、浮标、水生通讯系统组成,在实际工程中浮筒式单点系泊系统总是要求组件中锚链的倾角、水生通讯系统的倾角尽量小。罗晓健[1]等人采用准静力、动力分析法研究单点系泊系统,李焱等[2]采用Miner线性累计损伤理论和雨流计数方法研究多浮筒式系泊系统,夏运强等[3]采用调查分析、模型试验、理论研究工程实例等对浮筒式单点系泊系统进行研究,但均没有给出系泊系统中各个组件的倾角公式,并且思路较为复杂,为此本文根据浮筒式单点系泊系统,基于物理学的思想分析系泊系统中的各个组件,并结合MATLAB仿真技术给出一种选择锚链的倾角、水生通讯系统的倾角的选择方法,以及如何选择锚链型号、重物球质量、浮标吃水深度的合理范围的方法。

1 浮筒式单点系泊系统的简介

某浮筒式单点系泊系统由底面直径2 m、高2 m、质量为1 000 kg的圆柱体代替;系泊系统由4节长度为1 m直径为50 mm质量为10 kg的钢管、长1 m外径30 cm的钢桶、重物球、某种型号的电焊锚链及质量为600 kg的特制的抗拖移锚组成;水声通讯系统安装在系泊系统中的钢桶内,总质量为100 kg,浮筒式单点系泊系统示意图如图1所示。

图1 浮筒式单点系泊系统示意图Fig.1 Schematic diagram of floating-type single point mooring system

锚链选用无档普通链环,近浅海观测网的常用锚链型号及其参数如表1所示。钢桶上接第4节钢管,下接电焊锚链。该系统的约束条件:钢桶的倾斜角度(钢桶与竖直线的夹角)超过5°时,设备的工作效果较差。锚链末端与锚的链接处的切线方向与海床的夹角不超过16°,否则锚会被拖行,致使节点移位丢失。

表1 锚链型号和参数表Table 1 Cable model and parameter list

本文所研究的问题为浮筒式系泊系统的设计问题,即为确定锚链的型号、长度和重物球的质量,使浮标的吃水深度、游动区域及钢桶的倾斜角度尽可能的小。

2 系泊系统的设计

系泊系统的优化设计,实际上就是根据海域的实际情况,确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。

我们以浮标为坐标原点,假设浮标固定在海平面的位置不动,只是可以改变吃水深度。首先设定一吃水深度(一般以海平面静止时的浮标吃水深度),然后根据浮标的受力平衡,可获得浮标对第1个钢管的作用力。由静力学原理[4-5],再根据力的平衡和力矩的平衡,可以获得后续各个钢管、钢桶、锚链的倾角和坐标,从而获得整个锚链形状和游动区域,也可以获得抗拖移锚相对于浮标的位置包括深度和水平距离。

随后,调节浮标的吃水深度,得到抗拖移锚相对于浮标的深度。只有在一定的吃水深度条件下,抗拖移锚的深度恰好为海水深度时,则这个吃水深度为本题目的恰当吃水深度,从而可求得该吃水深度下的钢桶和各节钢管的倾斜角度、锚链形状和型号、浮标的吃水深度和游动区域。

2.1 浮标的受力平衡分析

浮标在稳定情况下的受力分析如图2所示。

图2 浮标受力分析示意图Fig.2 Schematic diagram of force analysis of the buoy

浮标受到重力(m浮g)、浮力(ρgV排)、风力(F风=0.625Sv2)(或者加上水流力)以及第1个钢管的拉力(T)作用。其中,钢管对浮标的拉力可以分解为水平分力(T水平)和垂直分力(T竖直)。

浮标稳定在水面上时,水平方向和垂直方向的合力分别为0,从而可以得到如下两个公式:

T水平=F风

(1)

T竖直=F浮-m管·g

(2)

2.2 组件的受力分析及倾角表达式

在以下受力分析时仅考虑水下物体的水下质量,即已经减去浮力作用,浮力不再另外考虑。由于通常重物和锚链的密度远大于海水密度,本文中忽略重物和锚链体积,用重物和锚链的实际质量代替水下质量,并忽略海水运动时对重物和锚链的水流力。

各钢管在稳定情况下的受力分析如图3所示。

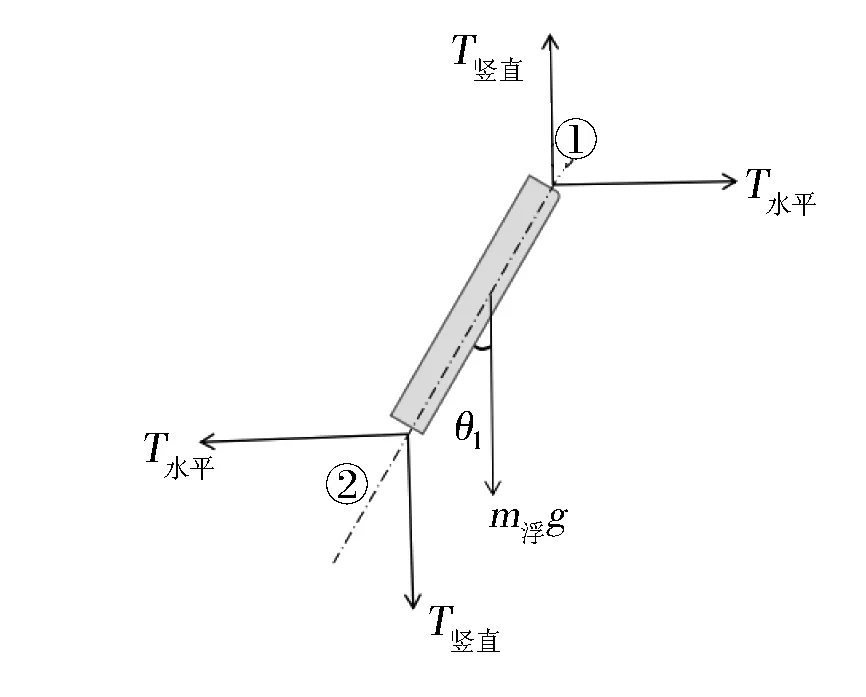
图3 第1个钢管的受力分析示意图Fig.3 Schematic diagram of force analysis of the first steel tube

选定该钢管下方的节点(命名为②)为支点,该钢管的各个受力会产生一定的力矩,稳定情况下,总力矩的和应为0,从而可得

(3)

式中:L1为每节钢管的长度;F风=0.625·S·v2;F浮=ρ·g·V排;m管为钢管的质量;T竖直为钢管的拉力T的竖直方向的分力;θ1为第一节钢管与竖直方向的夹角。

求解方程(3),可得θ1:

(4)

其他各个钢管分析方法类似,然后选钢桶(水声通讯系统)为研究对象,其受力分析如图4所示。

图4 钢桶的受力分析示意图Fig.4 Schematic diagram of force analysis of the steel drum

选择⑤为支点采用与钢管受力分析相似的方法,则由受力示意图并结合受力平衡可得到

T水平=F风

(5)

T竖直=F浮-4·m管·g-m桶·g-m重物·g

(6)

(7)

求解上述三个方程,可以得到钢桶与竖直方向的夹角θ5:

(8)

2.3 锚链的受力分析及角度

锚链由许多小节组成,对每节链的下端节点作为支点进行力矩平衡分析,可依此确定锚链中每一小节与竖直方向的夹角,并根据每节链的受力平衡原理递推下端节点在水平方向和竖直方向的弹性分力,进而得到第i节锚链与竖直方向的夹角θi的递推关系式,可以拟合出锚链的形状:

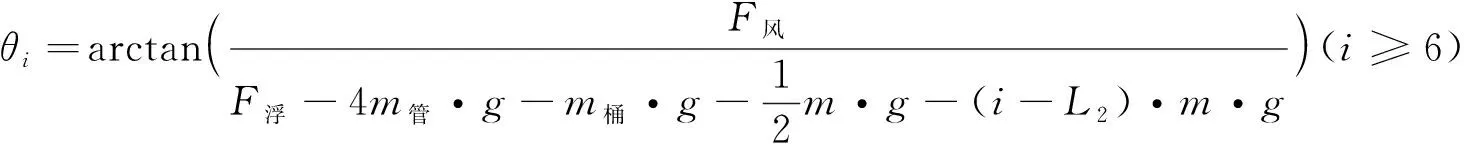
(9)

其中的m为每节锚链的质量,L2为每节锚链的长度。

3 系泊系统的优化设计

考虑潮汐等因素对被测海域水深、海水速度和风速的影响。若增加了水流对系泊系统的影响,即增添水流的作用力分析同系泊系统的设计分析方法类似。[6]

采用同样的分析方法,分别进行受力分析,以及力和力矩平衡的分析,可得

T竖直=F浮-m管g

(10)

T水平=F风+Fwb+Fwg

(11)

(12)

(13)

同理可得第i个钢管与竖直方向的夹角的递推公式:

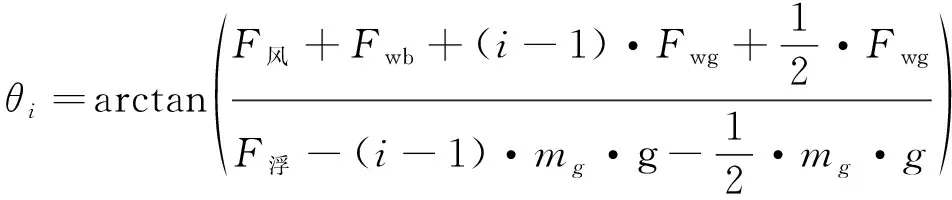
(14)

其中Fwb为水对浮筒的作用力,Fwg为水对钢管的作用力,然后对钢桶进行受力分析如图5所示。

图5 水流作用下的钢桶受力图Fig.5 Schematic diagram of force analysis of the steel drum under the effect of water current

根据力矩平衡可得方程：

进一步简化该方程,可得钢桶与竖直方向的倾斜角θ5的表达式:

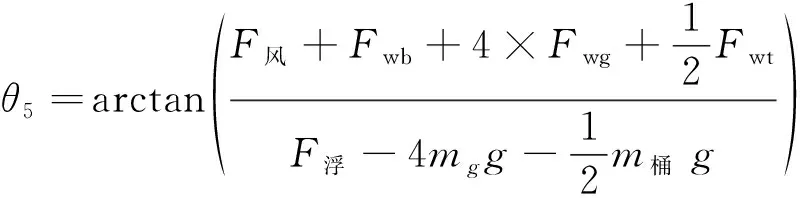
(15)

由于锚链具有较大空隙,我们忽略了水流对锚链的作用力,同样考虑力矩平衡对i个锚链节点进行力矩平衡,可得到i节锚链与竖直方向的夹角θi的递推关系式,进而可以拟合出锚链的形状:

(16)

其中的m为每节锚链的质量,L2为每节锚链的长度。

4 利用MATLAB仿真

4.1 风速对系泊系统的影响

针对系泊系统中的各个组件,将上述各个数学方程应用MATLAB编程分别求解其角度(与垂直方向的夹角),从而得到钢桶和各节钢管的倾斜角度、锚链形状和游动区域。首先在MATLAB中仿真模拟风速为0时的情况,计算得到此时浮标的吃水深度,在此基础上我们又研究了风速为12 m/s的情况。为了使浮标的吃水深度足够小,就可能会有部分锚链卧在海床上。根据受力分析,我们计算得到有60节锚链卧在海床上。在这种情况下,浮标的吃水深度计算可得,为0.535 7 m。设定了该吃水深度,我们运行MATLAB仿真模拟,分别求解上述各个关于θ的方程,从而求得各个钢管、钢桶、锚链的倾角和相对于浮标的位置,以及锚链形状和浮标游动区域。模拟结果表明,末节锚链与海床夹角为0°,说明此时系泊系统处于悬系状态。

类似的,针对24 m/s的情况,我们研究发现,所有的锚链都离开了海床,并对锚链在垂直方向有一定作用。这种情况下,我们分别设定了一系列的吃水深度,求得各个钢管、钢桶、锚链的倾角和相对于浮标的位置,从而获得整个锚链形状和游动区域,也可以获得锚定相对于浮标的位置包括深度和水平距离。只有合适的吃水深度,才可以使锚定的深度恰好为海水的吃水深度。则这个吃水深度就是本题目中的实际吃水深度。模拟结果表明,末节锚链与海床夹角为2.4°,说明此时系泊系统处于抓系状态。表2中给出了两种风速下的模拟结果。

表2 不同风速条件下的模拟结果Table 2 Simulation results at different wind speeds

4.2 不同风速下锚链形状

根据各个组件的倾角,可以获得每个组件相对浮标中心的位置,从而可以得到锚链形状曲线,如图6所示。

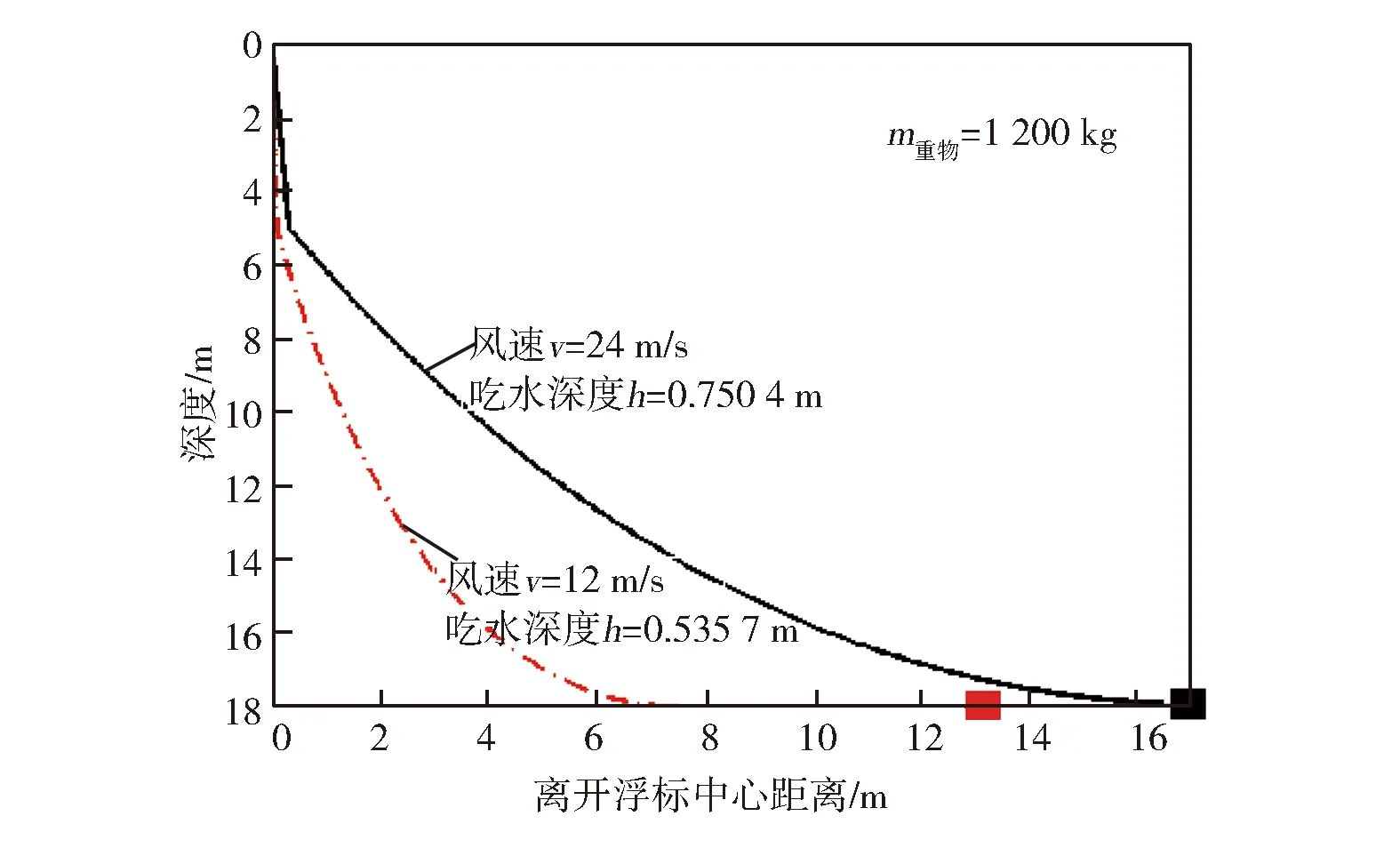
图6 不同风速下的锚链形状曲线Fig.6 Simulated curves of cable shapes under different wind speed

模拟结果显示:

1)风速对浮标的游动区域影响较大。风速为24 m/s时,浮标的游动半径为16.963 4 m;当风速为12 m/s时,浮标的游动半径减小为13.510 0 m。

2)风速小的时候,吃水深度小,风速大的时候,吃水深度增加。

3)风速小的时候,系泊系统部分锚链平卧在海床,对锚作用力仅在水平方向,系统处于悬系状态;当风速大于某个强度的时候,系泊系统末节锚链对锚处于抓系状态,容易产生移位,且系统可能处于不稳定状态。

4.3 重物球对系泊系统的影响

在MALTAB中继续仿真模拟,继续增大风速,当风速过大时,仅仅调整浮标的吃水深度,无论如何都可能无法使这个系统处于稳定状态。比如,当风速为36 m/s时,发现重物球M重物=1 200 kg的配重给出的锚链末端的切线与海床的夹角大于16°,而且钢桶的倾角大于5°。因此,该条件下,系统处于不稳定状态。适当增加重物球的质量,模拟结果如表3所示。

表3 不同重物情况下得到的模拟结果对比Table 3 Comparison of the simulated results for different weights

为了使系统保持稳定,需要增加重物球的质量。模拟结果表明,重物球的质量大于2 200 kg时,钢管和钢桶与垂直方向夹角小于5°,末节锚链切线与海床夹角也小于16°。随着重物球质量的增加,系统越来越稳定,浮标的游动半径逐渐减小,钢桶的倾角也在变小如表2中所示。相应于这三种典型配重,图7中给出了锚链形状。

图7 不同质量的重物球对锚链形状的影响Fig.7 The effect of the ball weight on the cable shape

综合上述模拟结果,我们发现如下几个结论:

1)增加重物球的质量,可以减小钢桶的倾角以及锚链末端和海床的夹角;

2)增加重物球的质量,使浮标的吃水深度也相应增加;

3)在2 200 kg和3 500 kg之间,浮标游动半径的差异并不明显。

考虑到锚链和钢管等材料的应力有限,我们认为2 200 kg的重物球不仅可以使钢桶的倾斜角度小于5°,锚链在锚点与海床的夹角不超过16°,而且使浮标的吃水深度也较小。

4.4 潮汐对系泊系统的影响

将潮汐影响下的各组件倾角的数学方程在MATLAB中仿真模拟,且假设布放海域的实测水深介于16 m～20 m之间。布放点的海水速度最大可达到1.5 m/s、风速最大可达到36 m/s。则为了使系泊系统能够全天候正常工作,则要求该系统可以工作的最大水深为20 m、最大海水速度为1.5 m/s、最大风速为36 m/s的极端条件下。并忽略了水流对锚链的冲力,水深、风速和海水速度会显著影响重物球的质量,同样会影响锚链的型号和长度。

以表3中的给出的五种锚链为例,分别仿真优化了使用各种锚链时浮标的吃水深度和游动区域及钢桶的倾斜角度如表4所示。表中给出了在临界稳定状态(也就是钢桶倾角约为5°,锚链末端与海床夹角约为16°)情况下,所需五种锚链的最小节数、重物球的质量和最小吃水深度。同时也给出了相应的浮标游动半径(R)。由于潮汐等因素的影响,海水深度减小,风速和水流速度也可能较小,设计的系泊系统则处于更稳定的情形。

表4 五种锚链型号对应的优化设计Table 4 Optimized design of five cable types

从系泊系统的优化设计的角度,也就是满足浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小的要求,对锚链型号的选择给出了合理的选择。不同类型的锚链,临界稳定状态下,锚链的形状也不同,如图8所示。

图8 海底深度为20 m时锚链形状Fig.8 Cable shape at a depth of 20 m

分析和小结:

1)各种型号的吃水深度近似相等;

2)从表3中给出的模拟结果可以看出,如果选用第一种型号的锚链,至少需要310节;如果选用第五种型号的锚链,则仅仅需要93节就可以;

3)锚链型号对浮标游动区域的影响较大。第一种锚链游动半径最大,第二到第五种锚链对应的浮标游动区域逐渐变小;锚链型号的对所需的重物球的配重也有显著影响。越粗的锚链,所需的重物球质量越小。第一种型号的锚链所需的重物质量最佳m重物=4 100 kg,第三种型号的锚链所需的重物质量m重物=3 900 kg,对于第五种型号的锚链仅仅需要m重物=3 700 kg;

4)研究结果表明,从系泊系统的优化设计的角度,也就是使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小的要求,本文可以用于优化锚链型号的选择以及系统参数的优化设置。针对本研究给出的五种型号选择,V型锚链最佳。

5 结束语

本文从力学原理出发并结合MATLAB仿真技术给出一种系泊系统设计的方案,为今后系泊系统中重物球、浮标吃水深度、锚链型号等的选择有借鉴经验。