无中继光传输系统中KNN非线性补偿技术研究

田 霖，林 睿，龙 函，徐 健，朱一峰，徐自闲，陆国生，陈保豪

(1. 中国南方电网有限责任公司超高压输电公司，广州 510623；2. 武汉光迅科技股份有限公司，武汉 430074)

0 引 言

分布式拉曼放大无中继传输技术主要通过在发送和接收端注入拉曼泵浦激光，利用传输光纤对信号实现分布式放大，具有建设和维护成本低等优点，在电力、军事和岛屿间通信等场景应用广泛[1-3]。目前，延长单跨无中继距离的技术主要可以分为两大类：一类是针对噪声受限系统，通过提升系统的光信噪比(Optical Signal Noise Ratio, OSNR)以尽可能地延长无中继单跨距离，其主要方式包括利用新型超低损光纤和遥泵放大等新型低噪放大方式[4-5]；另一类是针对非线性受限系统，主要通过非线性补偿技术来延长无中继单跨距离，目前最有效的非线性补偿技术是数字背向传输算法[6-7]，该算法在理论上可实现链路非线性效应的完全补偿，但其计算复杂度高。近些年，机器学习算法被广泛应用到光纤通信系统中，实现了诸如调制格式识别、性能监测和均衡等[8-9]。基于机器学习算法的非线性补偿技术，特别是针对分布式拉曼放大无中继传输系统中的非线性补偿技术还有待进一步研究。本文针对112 Gbit/s偏振复用—正交相移键控(Polarization Division Multiplexing-Quadrature Phase Shift Keying，PDM-QPSK) 350 km色散管理分布式拉曼放大无中继光纤传输系统，研究了基于K最邻近(K-Nearest Neighbors，KNN)聚类算法对链路光纤非线性的补偿效果以及K值对非线性补偿性能的影响。仿真结果表明，在系统误码率(Bit Error Rate，BER)为10-3时，经KNN算法非线性补偿后，输入端信号的光功率可提升约1 dBm。该技术可用于早期部署的低速直接检测色散管理无中继光纤传输系统(如：早期电力光纤通信系统)到高速相干检测系统的升级，以提升系统抗非线性能力。

1 KNN算法原理

KNN算法常用于对数据进行分类。对于QPSK信号，根据信号点在星座图中的分布可以将其分为4类，并将每一类分别标注为对应的标签L={1，2，3，4}，如图1所示。为利用KNN算法实现QPSK信号的非线性补偿，我们将从接收到的QPSK复数信号中随机选取N个样本x={x(1)，x(2)，…，x(N) }进行训练，剩下的M个样本y={y(1)，y(2)，…，y(M)}进行测试。然后按照如下过程对测试样本进行分类[9]：

(1) 按照图1所示的规则对测试数据进行标签标记，得到带有标签的测试数据集{(y(1),L(1))， (y(2),L(2))，…，(y(N),L(N))}。

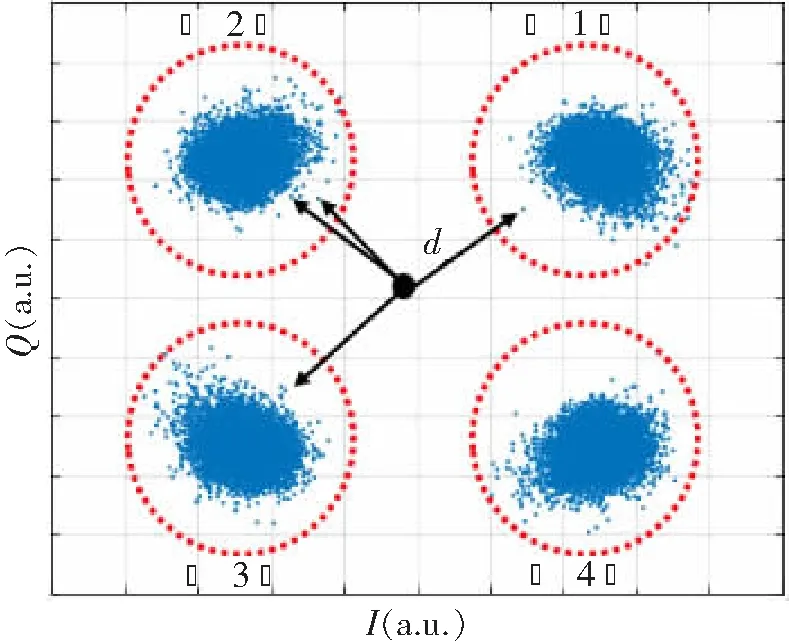
图1 QPSK信号星座图和对应标签

(2) 计算每个测试数据到所有训练数据点的距离d，其中第i个测试样本到第j个训练样本的距离d[(y(i),x(j))]可定义为

式中，Re{·}和Im{·}分别为取实部和虚部。

(3) 对每个距离进行排序，然后选择出距离最短的K个点。

(4) 对K个点所属的类别进行比较，根据少数服从多数的原则，将测试样本点归入到K个点中占比最高的那一类。例如，取K=5，若某一个测试样本y(n)到训练点距离最近的K(K=5)个点所对应的标签分别为{2，2，3，4，1}，则将该测试样本标记为第2类样本点。

2 仿真系统

图2所示为PDM-QPSK色散管理分布式拉曼放大无中继光纤通信系统框图。系统由发送端、传输链路和接收端组成。发送端用于产生112 Gbit/s 的PDM-QPSK信号，其主要由激光器、I/Q调制器和电信号源构成。激光器产生的连续光被偏振分束器分成偏振态正交的两路光并分别送到上下两臂的I/Q调制器进行电光调制。其中，激光器的中心频率和线宽分别为193.0 THz和10 kHz，电信号源产生驱动I/Q调制器的伪随机信号，波特率和码长分别为28 GBaud和213-1。上下两臂调制后的光信号经偏振合束器合成一路偏振态正交信号，最终得到112 Gbit/s PDM-QPSK信号。传输链路由两段色散补偿光纤(Dispersion Compensation Fiber, DCF)和一段标准单模光纤(Standard Single Mode Fiber, SSMF)构成，其中，每段DCF长度约为30.7 km，SSMF长度约为289.6 km，链路总长度约为350 km。DCF和SSMF的损耗系数和非线性系数均设置为0.2 dB/km和1.3 W-1/km，色散参量分别设置为17和-80 ps/(km·nm)-1。 光纤链路的损耗采用双向拉曼分布式放大进行补偿，其中拉曼泵浦源的中心波长均为1 450 nm，且前向和后向泵浦的功率分别为0.4和0.8 W。接收端，信号经放大和滤波后注入到相干接收机进行相干检测，注入到相干接收机的信号光功率和本振光功率均为10 dBm。本振光的中心频率和线宽分别为193.0 THz和10 kHz。经相干检测后的4路电信号送入到数字信号处理单元进行处理并最终解调出原始信号。数字信号处理单元包括：时钟恢复、恒模(Constant Modulus Algorithm ，CMA)均衡、载波相位恢复、KNN非线性补偿和解码。

图2 PDM-QPSK色散管理分布式拉曼放大无中继光纤通信系统框图

基于图2的系统框图，利用商用仿真软件VPI transmission Maker搭建了112 Gbit/s PDM-QPSK分布式拉曼放大无中继传输系统。在仿真过程中，每个偏振态信道的符号数为32 768个，总共2×32 768= 65 536个符号，每个符号的采样率为448 GSa/s。在接收端经过时钟恢复、CMA均衡和载波相位恢复后每个符号的采样率降为28 GSa/s，即对应每个符号一个采样点。然后针对x和y偏振信道，分别从对应的采样点中随机选取512个进行训练，剩下的用于测试。

3 仿真结果及分析

首先，我们研究了K值大小对补偿性能的影响。图3所示为系统总BER随K值变化的曲线和典型星座图。为保证系统工作在非线性受限状态，仿真过程中设置信号的入纤功率为13 dBm。图3(a)所示为信号仅经过时钟恢复、CMA均衡和载波相位恢复后的星座图(BER=1.18×10-2)。由图可知，此时信号已经历了较为严重的非线性损伤。由图3(b)可知，在K值从5到17的变化过程中，系统经KNN算法非线性补偿后的BER略有起伏。其中，当K=11时，非线性补偿后系统的总BER相对较低。需要指出的是，K值越大，非线性补偿算法的复杂度越高。从补偿性能和算法复杂度两方面综合考虑，后述性能分析时，K值均取11。

图3 系统总BER随K值变化的曲线和典型星座图

随后，研究了色散管理系统中不同入纤功率下算法的补偿性能。图4对比了接收端信号在有无KNN算法非线性补偿下，系统总BER随入纤光功率变化的曲线以及对应的典型星座图。其中，星座图(I)和(II)分别对应BER曲线中的(I)和(II)，即入纤功率分别为8和15 dBm。由图4可知，在入纤功率从-1 dBm逐渐增加到7 dBm的过程中，系统BER随信号入纤功率的增加而减小，即此时系统性能主要受噪声限制。在这种情况下，非线性补偿前后系统的总BER基本相等。这说明基于KNN算法的聚类算法对噪声引起的信号损伤基本不具有补偿效果。在入纤功率从7 dBm逐渐增加到15 dBm的过程中，系统BER随信号入纤功率的增大而增大，即此时系统主要受非线性限制。由图可知，在这种情况下，经KNN算法补偿后系统总BER有了明显的降低。特别地，在系统BER为10-3时，经KNN算法非线性补偿后输入端信号的光功率可提升约1 dBm。以上结果表明，针对色散管理链路，基于KNN算法的聚类算法能够有效地补偿链路光纤非线性引起的损伤。

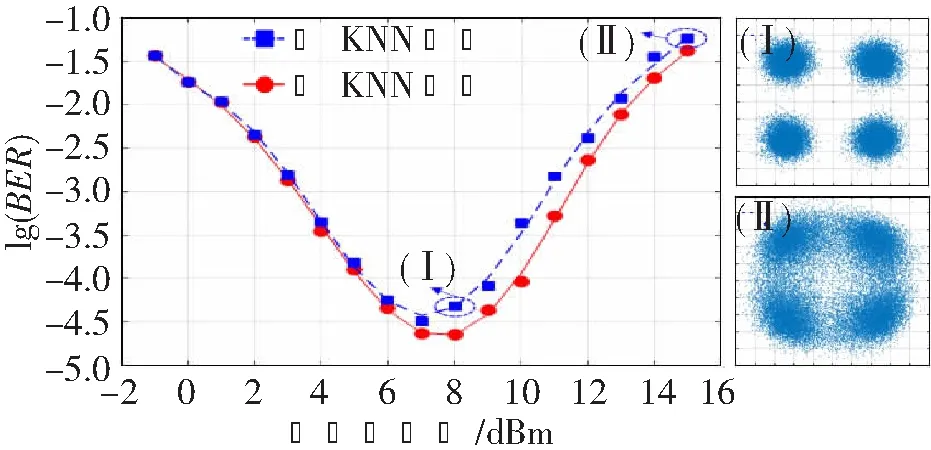
图4 系统BER随入纤功率变化的曲线和典型星座图@350 km色散管理系统

最后，进一步研究了非色散管理系统中不同入纤功率下算法的补偿性能。在非色散管理系统中，系统色散在时钟恢复后通过频域法进行补偿，然后再利用所提非线性补偿方法对非线性效应进行补偿。图5所示为350 km SSMF非色散管理系统中，经KNN算法非线性补偿前后系统BER曲线的对比结果和典型星座图。如图所示，星座图(I)和(II)对应的入纤功率分别为7和15 dBm。由图可知，对非色散管理系统，经KNN算法非线性补偿后，系统的误码性能改善十分有限。这主要是因为，在非色散管理系统中，由于色散和非线性的共同作用，信号相位和幅度的损伤比色散管理系统中更为复杂和严重。KNN算法补偿这种复杂相位和幅度损伤的能力有限。

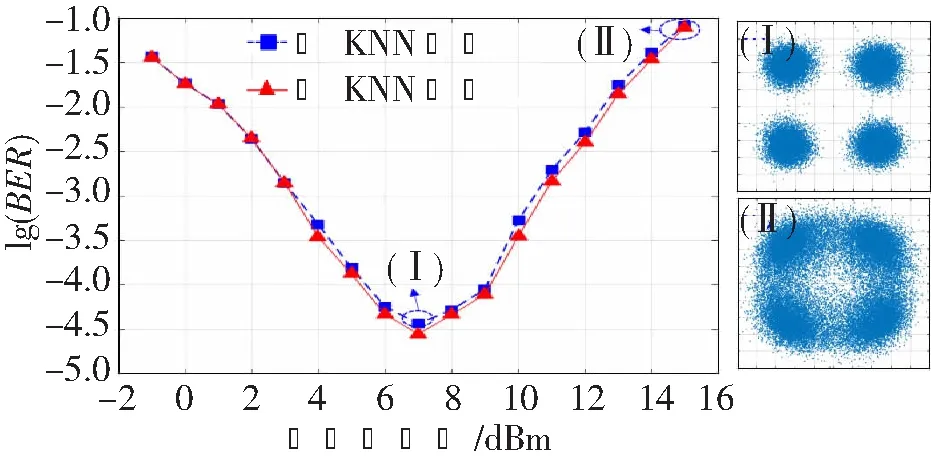
图5 系统BER随入纤功率变化的曲线和典型星座图@350 km非色散管理系统

4 结束语

本文搭建了112 Gbit/s PDM-QPSK 350 km色散管理分布式拉曼放大无中继光纤传输仿真系统。基于仿真系统研究了基于KNN聚类算法对系统光纤非线性的补偿效果以及K值对非线性补偿性能的影响。仿真结果表明，KNN聚类算法对色散管理分布式拉曼放大无中继系统中光纤非线性引起的信号损伤具有较好的补偿效果。针对本仿真系统，在系统BER为10-3时，经KNN算法非线性补偿后输入端信号的光功率可提升约1 dBm。