基于机器视觉技术的古陶瓷器型三维还原算法

张瑞瑞，周 强，王 莹，罗宏杰，张 静，王 芬

(1.陕西科技大学电气与控制工程学院，西安 710021；2.陕西科技大学材料科学与工程学院，西安 710021； 3.上海大学材料科学与工程学院，上海 200444)

0 引 言

我国陶瓷历史源远流长，文物资源丰富。随着我国人民物质生活的不断提高，愈来愈多的人对陶瓷文物产生了兴趣，古陶瓷的鉴定、保护和传承日益重要。在古陶瓷的鉴定过程中，产品的断源断代最为关键[1]，其技术难度也最高。自古以来主要的断源断代方法是利用“眼缘”[2]，即依靠鉴定人员长期积累下来的经验来判断，不可避免地融入主观因素的影响，更重要的是缺乏多元信息数据管理与大数据分析，致使隐藏在其中的许多有用信息被忽略或误读，这严重影响到古陶瓷技术的传承与发扬光大。

在多元的陶瓷产品信息中，产品器型具有鲜明的时代和地域特征，因此古陶瓷器型在鉴定中发挥着无可比拟的作用[3]。尤其是在当今的信息化时代，数字化的古陶瓷器型能够通过特征提取和分析，总结各个历史时期与不同窑口器物的结构特征，发现古陶瓷器型演变规律，为古陶瓷断源断代和真伪甄别提供参考依据，且对于深入研究陶瓷器型艺术特征与文化、审美之间的关系，甚至陶瓷器型与金属、玻璃器型之间的关系等，都十分重要。

但是由于古陶瓷产品器型的多样性和复杂性，使得精确提取陶瓷器型难度大，效率低，常规的测量方法通常难以获得器型的真实参数。而且大多古陶瓷真品保存在各大博物馆及私人收藏家之手，出于安全或隐私的考虑，这些陶瓷产品的拥有者或单位一般不愿意将其价格昂贵的古陶瓷接受仪器设备的扫描和数据采集，即使勉强同意也必须经过繁琐复杂的手续，使得古陶瓷数据三维扫描举步维艰。这些都造成了在当今信息膨胀的大数据时代，古陶瓷器型数字化资料严重欠缺的问题，从而严重制约了器型大数据研究的进程。

近年来，利用机器视觉技术将二维图像信息精确地还原为三维器型模型，已经成为古陶瓷研究的一个新方向。吴隽等[4]在撇口碗的曲线拟合方面做了一定工作，熊露等[5]对撇口碗的边缘特征进行了一定研究。虽然已经有不少研究者尝试利用各种图像处理方法获得古陶瓷器型，但是由于二维图像不同程度地存在图像畸变、图像背景复杂以及图像质量差别大等问题，使得提取到的器型模型误差大，还原出的三维器型变形严重。这些问题长期难以突破已经成为古陶瓷器型三维还原技术发展的桎梏。

为此，本文在解决复杂背景下轮廓提取、图像畸变校正等技术瓶颈的前提下，研制了一套基于机器视觉技术的古陶瓷器型三维还原算法，该算法能够通过图像增强、畸变补偿及曲线非线性拟合等机器视觉和模式识别技术构建古陶瓷器型的精确模型，以少量的参数获取完整的古陶瓷器型信息。

1 三维还原算法的结构

古陶瓷器型三维还原算法主要包括器型图像增强、图像畸变校正、古陶瓷器型建模和古陶瓷器型三维重现等模块。算法流程框图如图1所示。

图1 古陶瓷器型三维还原算法工作原理图Fig.1 Working principle diagram of 3D reduction algorithm for ancient ceramic vessel type

2 器型三维还原技术

2.1 低质量图像的器型边缘轮廓图像增强

从二维图像中精确提取古陶瓷器物轮廓是器型三维还原的第一步，但是由于目前形式多样、版本众多的古陶瓷图像普遍存在图像像素低、成像模糊、陶瓷器物与背景对比度低等图像质量问题，由这样的图像还原出来的三维模型与真实古陶瓷器型相差甚远，精度极低，甚至根本无法获得三维模型。为此，本算法先使用小波变换对图像进行边缘增强，提高古陶瓷边缘可辨识度，对古陶瓷边缘轮廓实现清晰提取和准确定位，具体过程为：

(1)原始图像的小波分解。

利用式(1)、式(2)对原始图像大小为M×N的图像f(x,y)进行二维离散小波变换，将原始图像分解成为含有图像轮廓信息的低频子图像带和以背景噪声为主的高频子图像带。

(1)

(2)

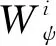
(2)滤除图像中的背景噪声成分

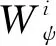
(3)

最后利用公式(3)的小波逆变换公式合成边缘增强后的图像[8]，可实现对图像边缘增强，达到突出陶瓷器物图像边缘轮廓的目的[9]。

2.2 基于二维透视变换的二维图像自适应视角校正

相机在二维成像时，由于拍摄角度、距离以及镜头差异等问题所造成的图像畸变现象，给器型的三维还原精度带来巨大的影响。为此本文提出一种利用椭圆霍夫变换的图像拍摄角度估计方法，精确估计相机相对于图像各个区域的拍摄角度，并在此基础上利用透视变换方法实现二维图像分区畸变补偿。具体步骤如下：

(1)根据古陶瓷的轮廓图像，提取其顶部和底足部分轮廓曲线；

(2)使用基于霍夫变换的椭圆轮廓检测算法[10]，拟合轮廓图像顶部和底足椭圆模型[11]；

(3)根据椭圆计算出该图像的拍摄角度。角度计算过程如图2所示。

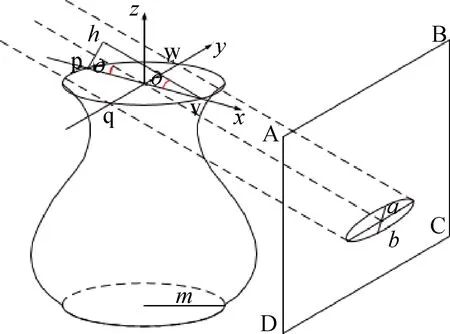
图2 拍摄角度几何模拟图Fig.2 Geometric simulation of shooting Angle

在理想条件下，假设相机为平行入射光线，相机以θ角度拍摄半径为m的陶瓷器型时，该器型顶部pqvw面在ABCD平面成像为一椭圆，拍摄角度可由式(4)计算得到，同理根据轮廓线提取器物下边沿轮廓线同样可以得出对于古陶瓷下边缘的拍摄角度θ下。

θ≈arcsin(b/a)

(4)

式中：a与b由图2中模型测量得到。

(4)图像纵向畸变矫正。根据上下两个角度θ上和θ下，可以估计古陶瓷二维平面每一水平截面的成像角度θi，利用式(5)对原始图像进行纵向的畸变矫正，式(5)中，l和l' 分别为矫正前后纵向尺寸。

l'=l/cos(arcsinθi)

(5)

(5)图像水平方向的畸变校正。采用透视变换算法[12]，根据畸变图像所在空间与标准图像空间线性对应的思想，通过透视变换矩阵，对图像镜头所造成的横向畸变进行校正，如式(6)所示。

(6)

2.3 基于神经网络技术的古陶瓷器形侧边缘建模

对经过畸变矫正后的古陶瓷边缘轮廓图像提取侧边缘轮廓基线，构建该基线的数学模型。该侧边缘轮廓模型的准确性，直接影响三维建模的效果。由于神经网络在原则上可以逼近任意非线性曲线，因此本文利用BP(Back Propagation)神经网络实现对古陶瓷侧边缘轮廓基线的精确建模。

构建输入层、隐藏层和输出层3层神经网络[17]。其中网络的输入层和输出层均为1个节点，即输入层接收为1×1的侧边缘曲线横坐标数据，输出层对应生成1×1的侧边缘曲线预测的纵坐标数据。隐藏层激活函数选用非线性的Sigmoid函数对输入输出数据进行非线性映射。在构建网络隐层节点个数时，为了保证在网络的误差收敛到尽可能小的前提下，能够减少网络的训练时间，同时避免网络对样本的过拟合现象，经多次实验调整网络参数，最终选定使用30个神经元节点用于隐藏层神经网络结构搭建。为了保证训练精度，设定网络迭代次数为500次，训练过程中均为误差(MSE)收敛到0.001为止。

将样本和标签不断送入构建的BP网络中，通过对信号的正向传播和基于误差的参数反馈修改，网络根据偏差不断向梯度下降的方向，迭代调整各神经元节点的权值和阈值，直至误差降到目标范围内。这里直接给出本文神经网络传递公式，如式(7)、(8)所示。

y'l=f(w1lxi),l=1,2,…,L

(7)

(8)

式中:xi表示输入数据，这里表示i个横坐标;y'l表示隐藏层中L个神经元对应的输出;yi表示输出结果，这里表示i个由横坐标获取的纵坐标;w表示权值，f表示网络的激活函数。

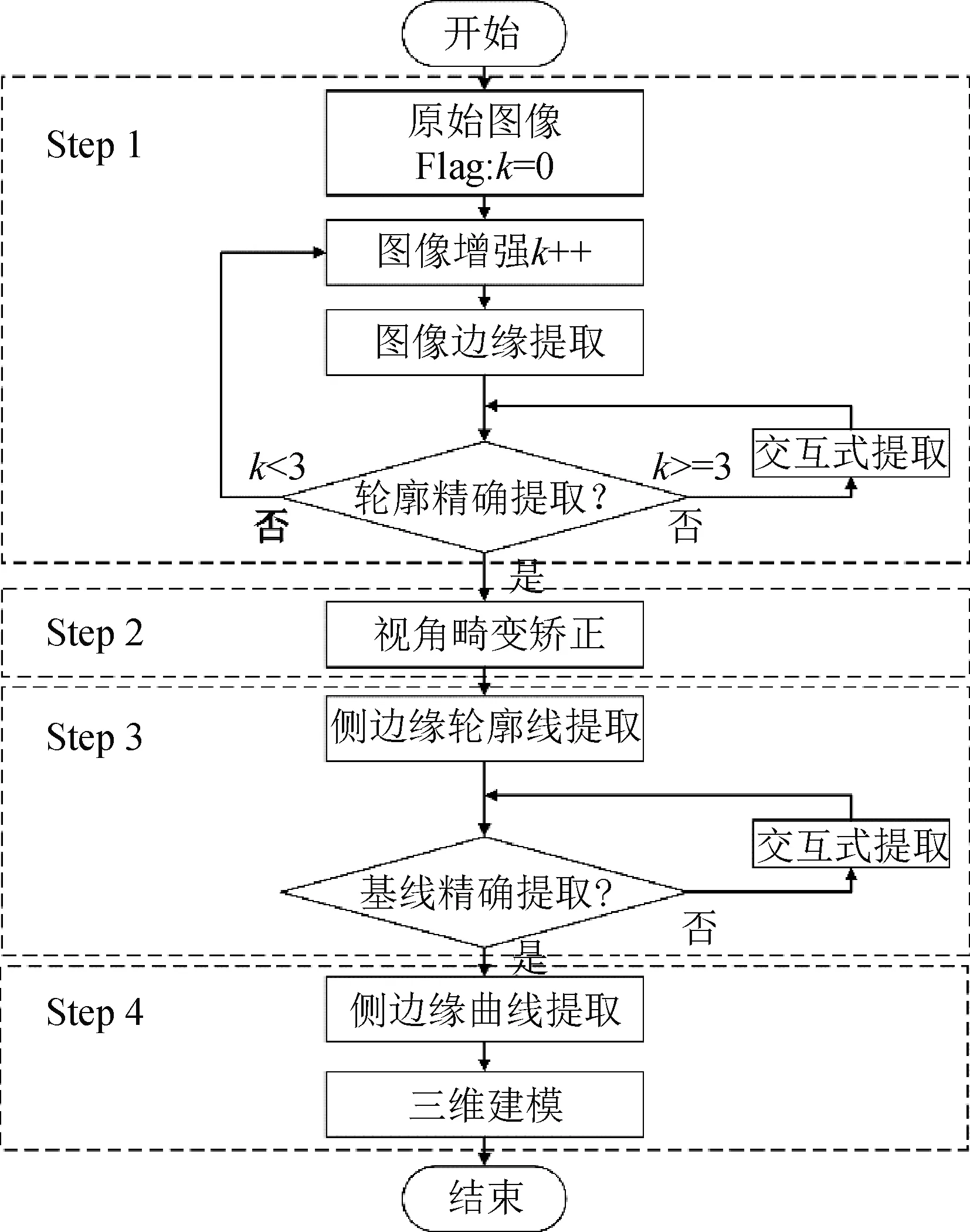
图3 算法流程框图Fig.3 Flow diagram of algorithm

BP网络建模的关键是训练样本和标签的获取。本文使用的样本和标签为侧边缘轮廓线对应的横纵坐标。将古陶瓷原始图像进行轮廓线提取和畸变矫正等处理后，根据轮廓边缘曲率变化对校正后的古陶瓷轮廓图像分别提取其左上、右上、左下和右下端点作为两条侧边缘轮廓线的起止端点，以此获取其准确的侧边缘曲线。之后再通过四个端点获取对称的中心轴线并以其为x轴，提取任意一条侧边缘轮廓线上的每一个像素点，映射其对应x轴的横纵坐标值，作为BP网络的训练样本，用于本文BP网络的样本及标签训练。

2.4 古陶瓷三维重现

BP神经网络建立的古陶瓷侧边缘轮廓曲线模型包含着旋转体古陶瓷器型的完整信息，可以作为器型的原始数据保存，因此可以通过该曲线模型，绕器型中心轴线旋转获取器型三维模型，即为最终古陶瓷器型三维重现模型。

2.5 古陶瓷器型三维重建算法流程

本文算法完整的流程图如图3所示。流程中k用来表示图像增强算法的使用次数，而交互式提取模块则是属于自动曲线提取不够精确时的辅助手段。其具体步骤如下：

(1)对读取的原始图像使用小波变换，在锐化增强轮廓的同时对图像降噪，再使用边缘检测算法提取图像边缘轮廓，图像增强算法可重复使用达到最佳效果，这里设定上限最多为三次，超出上限后使用交互式提取算法辅助提取；

(2)对提取的轮廓图像执行视角畸变校正算法，获取矫正之后的古陶瓷轮廓图像；

(3)对校正后的图像提取侧边缘轮廓基线，同时在程序中使用交互式操作辅助提取算法对其进行增强；

(4)将提取的侧边缘轮廓线使用神经网络建模，之后对其绕中轴线旋转，获取该旋转体古陶瓷图像的三维模型。

3 计算机实验与分析

使用上海大学文物器型非接触数字化扫描测量设备(SDGTC-2017)对古陶瓷器物进行三维模型扫描，以所获得的古陶瓷实物标准的点云数据作为标准尺寸，用于验证本文方法的准确性。

3.1 三维还原算法工作过程

本实验以常见的玉壶春瓶和采桑葡罐的二维图像作为还原对象，详细展示古陶瓷从二维图像到三维模型的完整还原过程。通过对二维图像的轮廓增强、视角畸变矫正、侧边缘轮廓曲线建模和器型三维重现等步骤完成对陶瓷器型的三维还原。还原步骤如图4和图5所示。Sample 1与Sample 2分别代指玉壶春瓶与采桑葡罐。

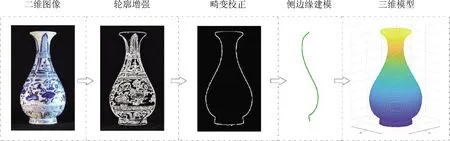
图4 玉壶春瓶三维还原步骤Fig.4 Steps of 3D restoration of the sample 1

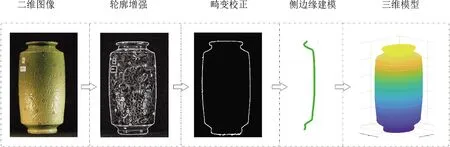
图5 采桑葡罐三维还原步骤Fig.5 Steps of 3D restoration of the sample 2

3.2 对本算法关键技术作用的分析

3.2.1 自适应视角矫正技术对提高三维还原精度的作用

通过仿真实验，分别采用本文的自适应视角矫正算法和传统畸变矫正算法提取古陶瓷侧边缘轮廓，然后对比二者的精度。实验结果如图6所示，图中的左右两条红色曲线为标准的玉壶春瓶侧边缘轮廓曲线，它是根据三维扫描仪获取的实物标准点云数据由插值函数拟合而成；左边的蓝色曲线为采取传统的视角矫正方法对二维图像进行处理后获得的玉壶春瓶侧边缘轮廓曲线；右侧的蓝色曲线为采用本文的视角矫正算法对二维图像进行处理后获取的玉壶春瓶侧边缘轮廓曲线。

对比发现：本文算法对于提高曲线拟合误差较大区域(图6中圈出部分)的拟合精度作用十分显著，使得整个陶瓷边缘轮廓曲线的拟合误差由原来2.6%下降为0.8%。

3.2.2 神经网络技术提高三维还原精度

为了验证BP神经网络拟合曲线的精度，通过实验对比本文的神经网络算法与传统多项式插值函数，比较两种方法在构建古陶瓷侧边缘模型上的精度差别。图7(a)为使用古陶瓷侧边缘曲线的样本数据训练BP网络时，MSE误差随迭代训练的收敛曲线。图7(b)为使用以上两种方法构建的采桑葡罐侧边缘轮廓曲线建模的效果图。

由图7(a)可知，500次迭代后，曲线MSE误差只有5.12×10-3左右，而由图7(b)可以看出，两种方法对采桑葡罐侧边缘建模的整体效果都比较好，但通过图8构建的采桑葡罐侧边缘局部轮廓细节模型效果图可看出，本文方法构建的曲线模型更为逼近采桑葡罐的颈部、尾部以及底座等形状较为奇异部分的轮廓细节，数据表明，其模型拟合精度的均方误差(MSE)仅为5.12×10-3，远小于传统方法的均方误差(MSE)1.82×10-2，为实现古陶瓷的三维精确还原打下坚实基础。

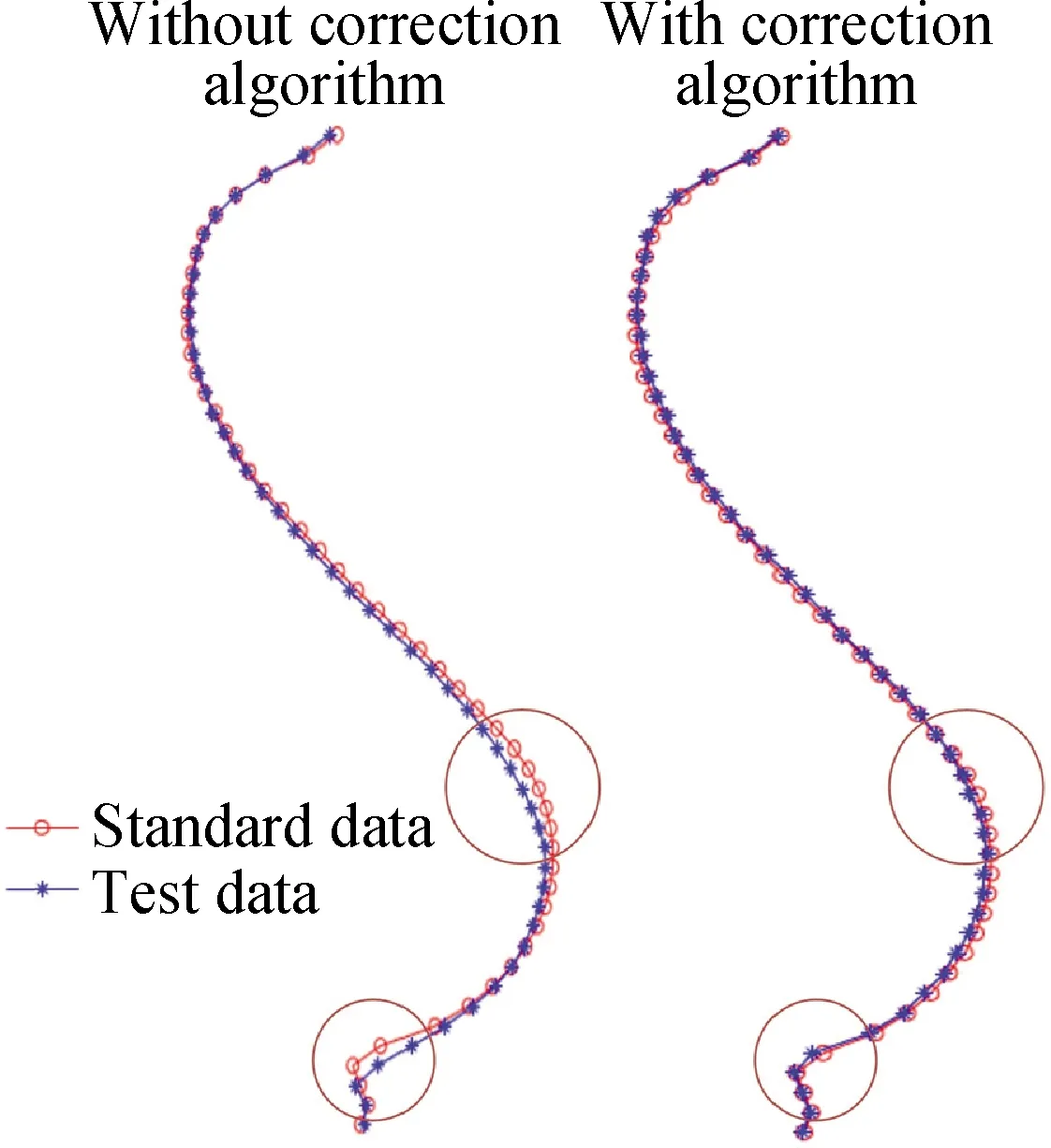
图6 对玉壶春二维图像侧边缘轮廓线畸变校正效果对比Fig.6 Compares of distortion correction effect of side edge contour curve of the 2D image of sample 1

图7 BP网络训练过程误差曲线(a)和采用2种方法构建的采桑葡罐侧边缘轮廓曲线模型的效果图(b)Fig.7 Error curve of BP network training process (a) and effect diagrams of side edge contour curve model of sample 2 with two methods

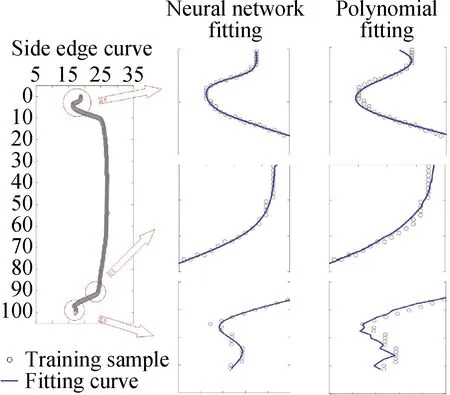
图8 采用本文及传统方法构建的采桑葡罐侧边缘局部轮廓细节模型的效果图Fig.8 Effect diagrams of side edge contour local detail model of sample 2 by using this paper's method and traditional method

3.3 三维还原算法精度实验

3.3.1 黑底红纹小嘴瓶和采桑葡罐图像三维还原实验

对黑底红纹小嘴瓶和采桑葡罐二维图像构建器型模型和器型三维重现的过程分别如图9与图10所示。为了验证算法还原精度，从三维扫描仪扫描实物获得的点云坐标数据中等间距提取50个点作为标准数据，用于检验算法构建器型模型的精度。Sample 3代指黑底红纹小嘴瓶。

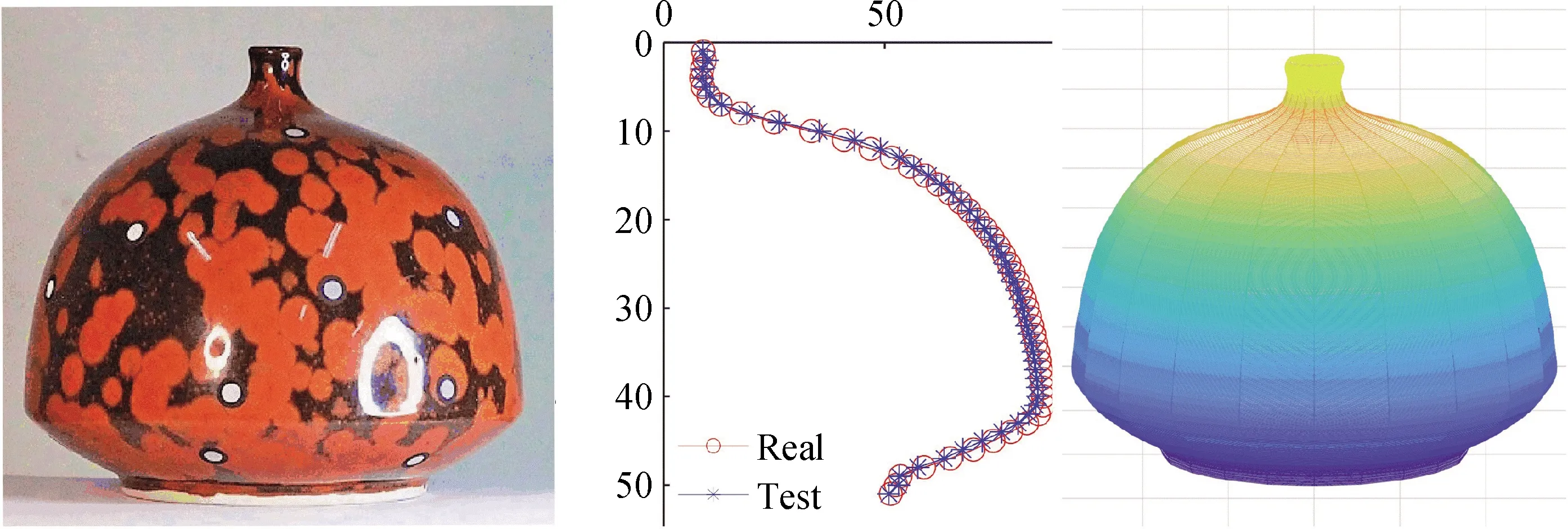
图9 黑底红纹小嘴瓶三维还原对照图Fig.9 3D reduction control diagram of sample 3

图10 采桑葡罐三维还原对照图Fig.10 3D reduction control diagram of sample 2

3.3.2 黑底红纹小嘴瓶和采桑葡罐图像三维还原的鲁棒性和精确性实验

通过改变拍摄角度、拍摄距离获得不同古陶瓷二维图像，用以验证该算法三维还原的精确性和鲁棒性。

具体测试数据如表1所示。其中测试距离为相机镜头距离古陶瓷中心距离，测试角度为镜头中心对准古陶瓷器物中心时镜头与水平地面之间的夹角，使用可取度表述不同条件图片的成像质量，H_NRMSD为纵向正规化均方根误差百分数，W_NRMSD为水平方向正规化均方根误差百分数。

将拍摄的不同距离、不同角度下的两种器型图像，使用本文算法流程获取其三维还原模型与标准模型数据对比，分析发现本算法在H_NRMSD和W_NRMSD指标下的误差均在1.7%以内，可知本算法利用二维图像还原三维器物的还原精度高，其适应拍摄条件变化的鲁棒性强，克服了传统三维还原方法中无法彻底解决的图像畸变、轮廓模型非线性等技术难题。

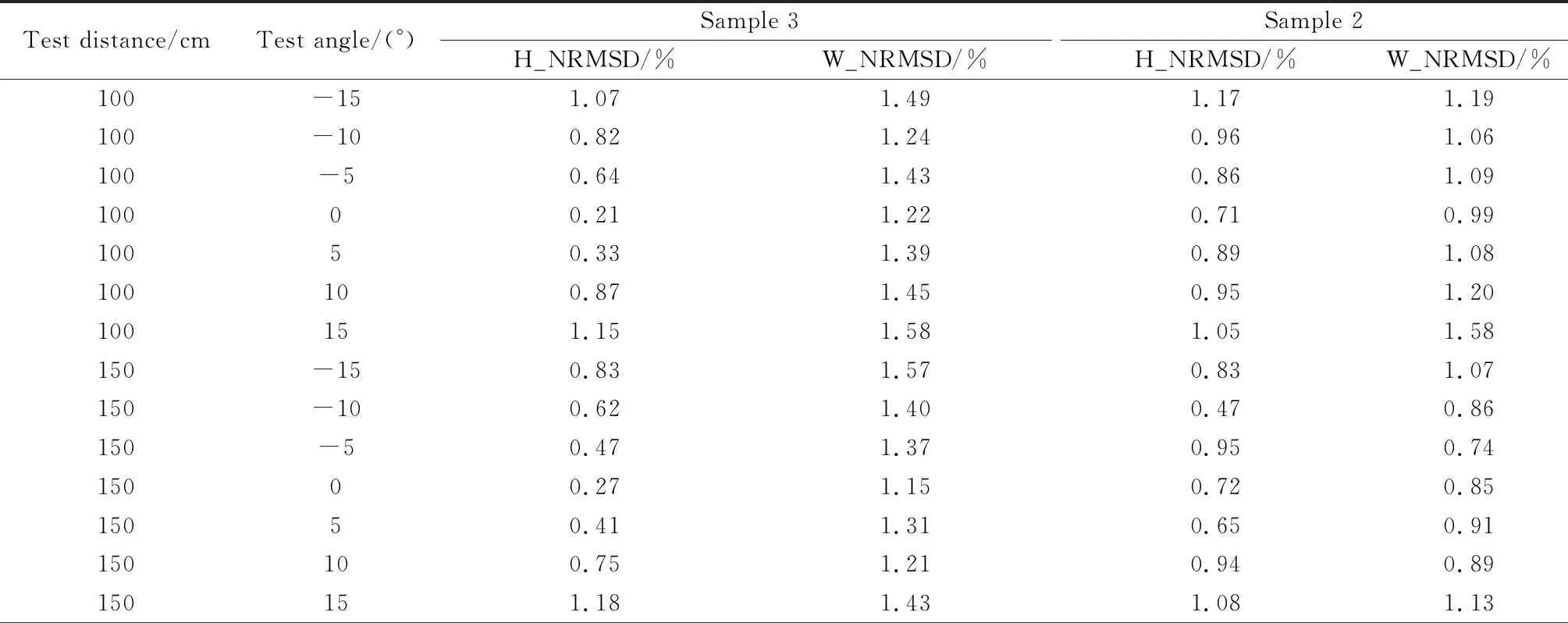
表1 黑底红纹小嘴瓶和采桑葡罐测试数据Table 1 Test data of the sample 3 and sample 2

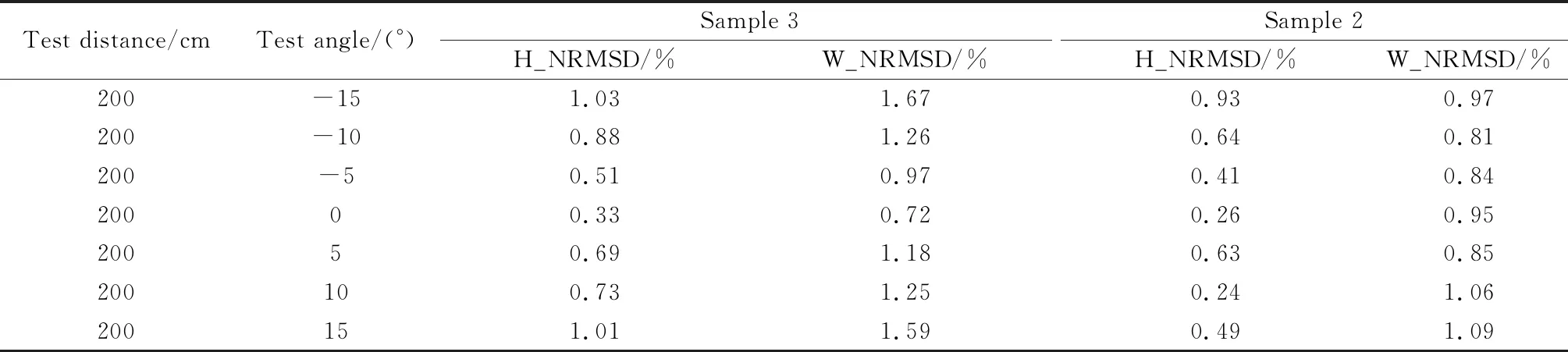
续表

3.3.3 玉壶春瓶图像三维还原的精度实验

为了进一步检验该算法的还原精度，使用上海大学文物器型非接触数字化扫描测量设备和市面上的先进三维扫描仪EinScan-SP两种三维扫描仪分别对玉壶春瓶进行扫描，下文分别记为1号和2号扫描仪，综合两组点云数据提取的高度数据和侧边缘轮廓数据并与本文算法提取的数据进行对比分析，实验测试数据如表2所示，以1号获得的数据为标准值检验并对比本文方法和2号三维扫描仪的精度。表2中H1、W1表示本文算法构建的陶瓷器型轮廓模型在竖直和水平两个方向的精度，H2、W2表示2号三维扫描仪获取数据在竖直和水平两个方向的精度。

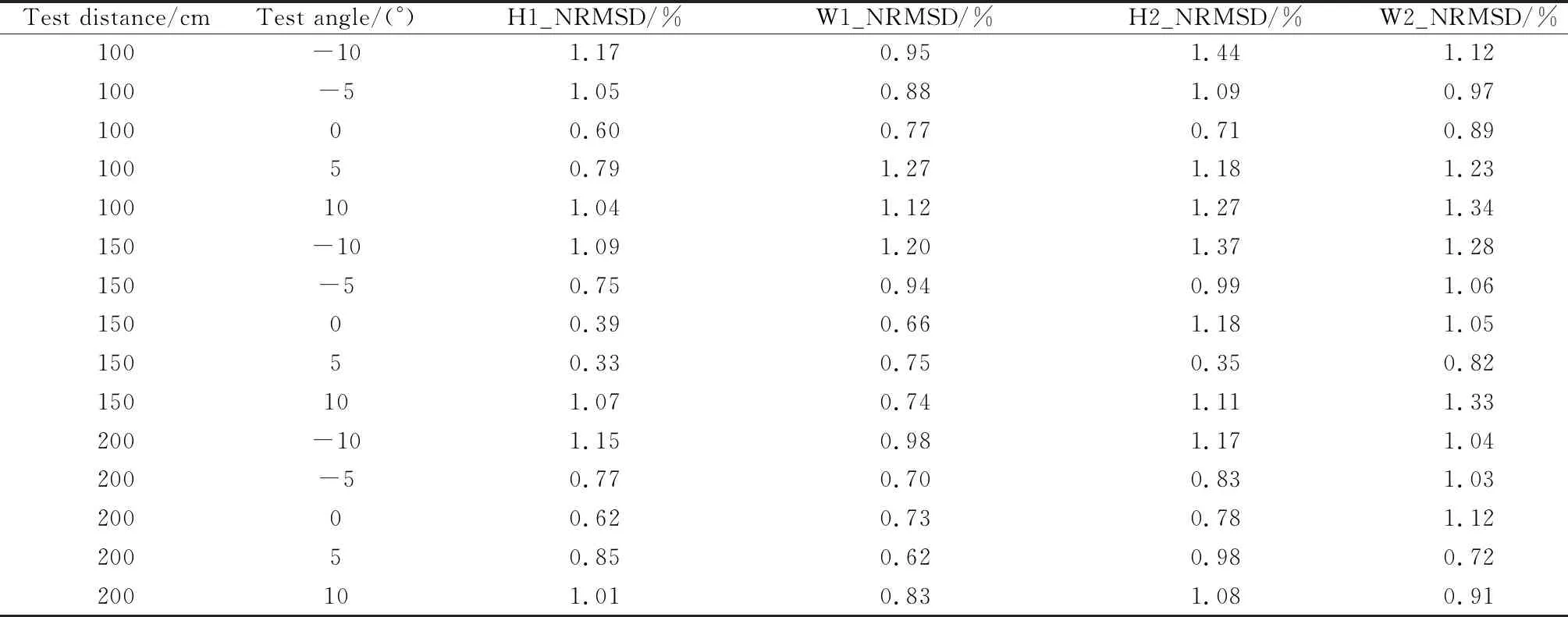
表2 玉壶春瓶测试数据Table 2 Test data of the sumple 1

根据表2测试数据可知，本文算法对器型侧边缘建模精度相比2号扫描仪更逼近1号标准数据，由图11能更直观地看到这一结论。

图11 玉壶春瓶侧边缘三组对照数据Fig.11 Comparison data of three groups of side edges of the sample 1

4 结 论

通过对器型图像增强、图像畸变校正、古陶瓷器型建模和古陶瓷三维重现等一系列算法的研究，获得了完整的古陶瓷器型三维还原算法。实验表明当拍摄角度从-10°～10°范围内，分辨率在4万像素以上时，本算法能以低于1.7%的误差精确还原陶瓷器物的三维模型。大大方便了古陶瓷的分析研究和复原展示工作，为古陶瓷器型研究提供了一种新方法。