面向大规模时间敏感网络的分组调度机制

邱雪松，黄徐川，李文萃，李温静，郭少勇

（1.北京邮电大学网络与交换技术国家重点实验室，北京 100876；2.国网河南省电力公司信息通信公司，河南 郑州 450052；3.国网信息通信产业集团有限公司，北京 102211）

1 引言

随着信息技术的飞速发展，在工厂自动化控制、自动驾驶和电力自动化等领域，对数据流传输的时延要求超出了传统以太网的可控范围[1]。为解决传统以太网中实时数据的可靠传输问题，IEEE 802工作组提出了时间敏感网络（TSN,time-sensitive network）的概念。TSN 支持时间触发流量（TT,time-triggered traffic）的传输，该类流量具有周期性传输的特点，并具有确定性的低时延要求。针对TT的调度问题出现了大量的研究[2-10]。

文献[2]使用可满足性模理论（SMT,satisfiability modulo theory）和优化模理论（OMT,optimization modulo theory）来实现有效调度。文献[3]基于整数线性规划（ILP,integer linear programming）计算式生成门控制列表，通过计算全局调度将资源最佳地分配给时间触发流量。文献[4]提出了一种混合遗传算法，用于生成时间触发流量的静态调度表，优化了时隙的分配数量并提高了传输效率。文献[5]提出了一种基于遗传算法的启发式调度算法，使用路由和调度的联合约束来生成静态的全局调度，从而使可调度性、传输效率和资源利用率得到显著提高。文献[6-7]基于ILP 提出了针对路由和调度联合问题的解决方案。文献[6]使用2 个性能指标（即端到端时延和调度能力）来评估不同流量模式和网络拓扑的实验结果。文献[7]利用ILP 解算器对参数变化很大的问题实例进行了求解，根据求解时长对算法的性能进行了评估。文献[8]基于SMT 提出了一种联合路由和调度的迭代算法，但是算法性能对流量之间传输路径的冲突程度敏感，导致成功率较低。文献[9-10]提出了时间敏感软件定义网络（TSSDN,time-sensitive software-defined network）的概念和用于计算调度的ILP 式，TSSDN 利用逻辑集中的控制平面来计算全局的调度方案。

上述研究通过不同方法给出了时间触发流量可行的调度机制，但是在大规模调度场景下的求解时间难以满足调度需求。为此，本文针对大规模时间敏感网络中时间触发流量的调度问题进行了研究，具体包括以下三部分。

1)建立了分组调度模型，在每一组流量的调度中，通过时间和空间上将待调度流量分离的时分多址（TDMA,time division multiple access）思想消除了排队时延，保证了时延的确定性。

2)针对网络拓扑规模庞大的问题，设计了一种拓扑修剪策略。通过减少不必要的约束条件简化调度模型，减少了调度的求解耗时。

3)针对流量规模庞大的问题，设计了一种基于谱聚类的流分组策略。通过分组调度的方式减少调度求解时间，同时保证较高的成功率。

2 数学模型

2.1 时延分析

时间触发流从源主机到目的主机沿着指定路径进行周期性传输，其端到端时延包括传播时延、发送时延、处理时延，当网络中发生拥塞时，还包括排队时延。时延分析如图1 所示。

图1 中，ti表示节点vi的发送时刻，dtrans、dprop和dproc分别表示发送时延、传播时延和处理时延。当发生排队时，排队时延为dqueu，D表示某个节点和下一节点之间的端到端时延，如式(1)所示。

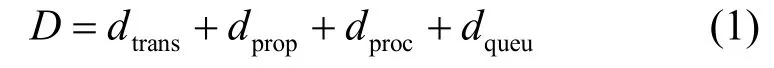
图1 时延分析

当不发生排队时，D只包含发送时延、传播时延和处理时延。传播时延由信道长度和介质中信号的传播速率决定，可以认为具有确定性。交换机内部的处理时延与其存储转发的能力有关，可以认为具有确定性。发送时延由帧大小和发送速率决定，也具有确定性。当网络中发生拥塞时，在交换机内部排队时间无法确定，导致产生的排队时延具有不确定性。

由于端到端时延的不确定性主要来源于可能包含的排队时延，因此在设计时间触发流的调度模型时，需要避免排队情况的出现，从而保证其传输的确定性。

2.2 调度模型

当多个数据分组试图在交换机的同一个输出端口进行传输时，会发生排队的情况，若在时间触发流传输时为其分配特定的链路资源仅供其传输，就可以消除排队的情况从而保证端到端时延的确定性。在时间上，可以在一个基本周期内为不同的时间触发流分配不同的时隙；在空间上，可以为不同的时间触发流分配不冲突的链路资源。通过这种在时间和空间上将不同时间触发流分离的时分多址思想，可以实现每个时间触发流到达交换机时，始终有一个空状态的队列为其开放，从而避免了排队情况的出现。

如图2 所示，一个基本周期被分为多个时隙，每个时隙从0～tmax编号，被分给特定的时间触发流进行传输，且时隙的长度足够宽，足以使最大传输单元（MTU,maximum transmission unit）的数据分组穿过最长的网络路径。

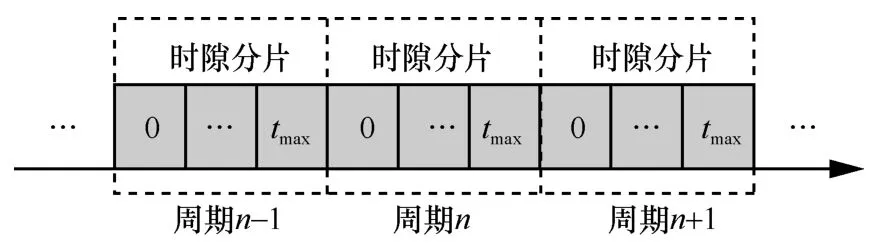
图2 基本周期的时隙分片

基本周期能提供的时隙分片数量有一个上限值。例如，对于1 Gbit/s 的链路，假设MTU 为1 500 B，数据分组允许穿越的最长网络路径为8 跳，则一个MTU 的数据分组穿越最长网络路径的总发送时延为1 500 B×8÷1 Gbit/s×8=0.096 ms。在仅考虑发送时延的情况下，5 ms 的基本周期最多可以提供5÷0.096≈52 个时隙分片，考虑到传输距离及交换机处理能力等影响因素，实际时隙分片数量的上限要更小一点。

网络的拓扑被建模为有向图G=(V,L)，其中V=S∪H是网络中所有节点的集合，S表示网络中的交换机，H表示终端的主机。L⊆V×V表示网络中相互连接的2 个节点之间的一条有向全双工链路。有序对(Vi,Vj)和(Vj,Vi)分别表示2 条独立的传输链路，有序对的第一个元素表示发送节点，第二个元素表示目的节点。定义网络中时间触发流的集合F为

所有的时间触发流按照特定的分组策略被分组为：G1,G2,…,Gmax−1,Gmax，其中max 表示分组的数量，在调度环节的每次迭代中完成一组时间触发流集合的调度。一组时间触发流集合Gm中所有流可能的传输路径的集合为

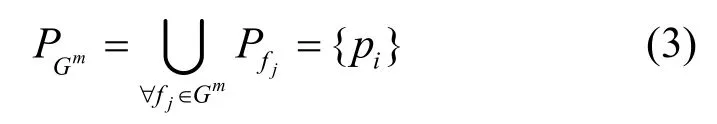
其中，fj=(s,d)表示集合Gm中的一个流，s和d分别表示fj的源主机和目的主机，表示流fj可能通过的路径的集合。在本文模型中，被设定为流fj最短路径的集合，于是PGm包括每个时间触发流fj∈Gm从源主机到目的主机的所有最短路径。时隙分片的集合T和所有链路的集合L分别如式(4)和式(5)所示。

定义如式(6)～式(9)所示映射。

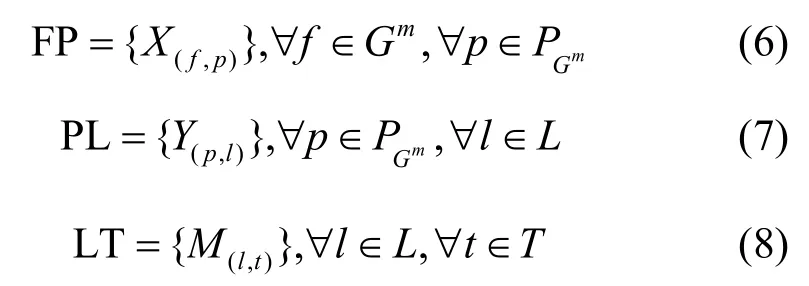
FP 为时间触发流和路径之间的映射，如果流f通过路径p从源主机到达目的主机，则X(f,p)=1；否则X(f,p)=0。PL 为路径和链路之间的映射，如果路径p包含链路l，则Y(p,l)=1，否则Y(p,l)=0。LT 为链路和时隙之间的映射，如果时隙t上的链路l在先前的迭代调度过程中已经被占用，则M(l,t)=1，否则M(l,t)=0。PT 为路径与时隙之间的映射，如果时间触发流沿着路径p在时隙t上进行了传输，则N(p,t)=1，否则N(p,t)=0。

定义如式(10)～式(12)所示约束。

约束条件(10)表示每一条路径最多只能分配到一个时隙上。每一个时间触发流最多只能分配到一个时隙上，由于该流最终只能选择一条最短路径进行传输，因此对于每个时间触发流而言，最多只能为其一条可能的最短路径分配时隙，则有约束条件(11)。如果具有相同链路的2 条路径应被分配到同一个时隙时，可能引起冲突，因此某条链路的某个时隙上最多只允许一个时间触发流进行传输，则有约束条件(12)。

在时间触发流量集合和网络拓扑已知的情况下，为了提高调度的成功率，调度机制应在保证时延确定性的前提下，尽可能地提高网络中能够容纳的时间触发流的数量。另外，由于一个时间触发流对应多个其可能传输的最短路径，但是最终只会选择其中一条进行传输，因此可以把时间触发流分配到时隙上的问题转化为把路径分配到时隙上的问题，则优化的目标是尽可能地提高分配到时隙中的路径的数量。某个流组Gm的调度模型可以形式化描述为

3 拓扑修剪策略与流分组策略

3.1 拓扑修剪策略

模型约束条件的建立与网络的拓扑具有密切关系。根据式(12)可知，拓扑结构中每一条链路在每一个时隙上都会为模型添加一条约束条件。而当拓扑规模更加庞大时，模型的约束条件数目会快速增加，从而导致问题的复杂程度急剧增加，最终导致求解时间不能被接受。

然而，对于一组待调度的时间触发流而言，每一个时间触发流最终只会选择最短路径集合中的一条路径进行传输，该组时间触发流可能占用的链路资源为最短路径集合中所有路径所包含的链路。因此，整个拓扑结构中剩余的链路在本组调度中不会有流通过，不可能发生同时传输的冲突情况。通过拓扑修剪的方式将本组时间触发流调度时的网络拓扑进行修剪，删除不会进行传输的链路，从而达到减少模型约束条件的目的。

图3 是上述拓扑修剪的一个示例。图3 (a)为网络原拓扑结构，网络中存在2 个待调度的流量，分别为flow1=(S7,S5)和flow2=(S3,S5)。flow1从源节点到目标节点有2 条最短路径，分别为path1和path2，而flow2从源节点到目标节点有2 条最短路径，分别为path3和path4。这4 条路径所包含的链路是本组调度可能占用的链路资源，每条链路都会为模型的求解添加约束条件。拓扑修剪之后的结果如图3(b)所示，链路的减少使模型的约束条件减少，从而降低了问题的求解规模。另外，由于拓扑修剪策略不会影响最终的调度结果，因此调度成功率保持不变。

图3 拓扑修剪示例

3.2 基于谱聚类的流分组策略

前文所述的调度模型是一个ILP 问题，该问题是一个NP-hard 问题。随着待调度流量数量的增加，模型的求解时间会急剧增加而变得不能被接受。首先对所有的时间触发流进行分组，然后对各个流组分别进行调度，即对每个流组的ILP 模型进行求解，并将所得的调度结果作为下一流组ILP 模型的约束条件进行输入，这种分组调度的方式可以将原来大规模的求解问题划分为较小规模的ILP 问题，从而在流的数量较多时，显著的减少最终的总耗时。

然而，这种分组调度的方式在对每组时间触发流进行调度时所获得的结果是一个局部最优的结果，最终的调度结果与原先的结果可能具有一定的偏差，从而导致调度成功率的降低。因此，在进行分组调度时，如何保证一定的调度成功率是首要考虑的问题。

谱聚类（SC,spectral clustering）[11]是一种基于图论的聚类方法，将带权无向图划分为2 个或2 个以上的最优子图，使子图内部尽量相似，而子图之间距离尽量远，所得结果是一个均匀划分，即各个划分所包含的节点数目相近。本文将谱聚类的思想引入分组策略的研究中。对于2 个待调度的流而言，如果它们各自可能传输的路径之间具有较多重叠的链路，则它们同时进行传输的难度也较大。同理，对于2 个流组而言，如果它们中所有的流可能传输的路径集合之间具有较多重叠的链路，则这2 个流组同时进行传输的难度也较大。因此，为了使分组调度之后的调度成功率尽可能高，各个流组之间路径集合的重叠链路应尽可能少。

用路径集相似度的概念来表示2 个路径集合之间的重叠程度，定义2 个流之间路径集相似度为

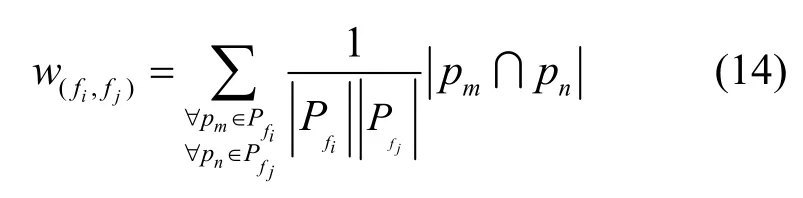
其中，w(fi,fj)是流fi和流fj的传输路径集合之间链路重叠程度的表征。对于流集F的一个划分，即G1,G2,…,Gmax−1,Gmax，其总路径集相似度为

基于流之间的路径集相似度来建立无向图ξ=(F,W)，其中顶点集F由所有时间触发流组成，边集W=F×F的权重表示2 个流fi和流fj之间的路径集相似度w(fi,fj)。2 个顶点之间相连表示对应的2 个流之间的路径集合存在一定的重叠链路，如果这2 个流之间的路径集合不存在重复链路，即路径集相似度为0，则对应的顶点之间不连接。图4 给出了待调度流量集合F={f1,f2,…,f8,f9}的一个划分，即G1={f1,f2,f8},G2={f3,f4,f9},G3={f5,f6,f7}。根据式(15)可知，图4 中虚线的权重之和表示该划分的总路径集相似度。

图4 待调度流量集合划分示例

考虑到模型求解耗时的问题，还应使各个分组的大小尽可能一致，避免出现某个分组过大的情况，否则会导致模型求解的总时间变得不再理想，而谱聚类均分划分的特点可以满足该需求。

因此，求解流的最佳分组问题被转化为求解基于路径集相似度构建的无向图ξ的最佳划分问题。在具体实现上，由于Python 中sklearn.cluster 的SpectralClustering 模块集成了谱聚类方法，将由路径集相似度构建的相似度矩阵M（Mi,j表示流fi和流fj之间的路径集相似度）和要分组的数目作为参数输入，即可获得分组结果。该结果是一个总路径集相似度最小且均匀的最佳划分，分组的结果G1,G2,…,Gmax−1,Gmax将被用于分组调度机制。

3.3 基于拓扑修剪策略和流分组策略的分组调度机制

分组调度机制的整体流程如算法1 所示。算法1 的整体输入为所有时间触发流的集合F、网络的拓扑结构G=(V,L)、分组数max，输出为路径和时隙的映射。最终获得的即为最终的调度结果。在初始化步骤中(算法的1)～3)行)，对F按照基于谱聚类的分组策略进行分组，从而得到分组结果G1,G2,…,Gmax−1,Gmax。另外还要对变量以及前一组流量的调度结果带来的约束进行初始化。在每一组的调度过程中，首先进行拓扑修剪，避免产生不必要的约束条件；然后进行ILP 模型求解，将得出的调度结果更新到中，并将本组调度带来的对后续调度的约束M(l,t)更新到中。

算法1分组调度机制

4 仿真实验和结果分析

4.1 实验环境

所提调度模型是一个ILP 问题，可直接采用CPLEX 或Lingo 等解算器进行求解，本文基于Python3.7 和IBM 的CPLEX（版本V12.10）进行了仿真实验。通过Python 的networkx 包生成网络拓扑，基于sklearn.cluster 的SpectralClustering 模块完成对调度流量的分组。实验思路是，通过不同调度规模下算法的仿真表现来验证其有效性。

仿真条件包括网络的拓扑规模和数量规模两方面，前者表现为网络中交换机的数目，后者表现为待调度流量的数目。模型的参数包括是否进行拓扑修剪（分别用1 和0 表示）、分组的数量、基本周期的时隙分片数量。

实验的仿真条件及参数如表1 所示。

4.2 仿真结果和分析

本节将分组调度机制与文献[9-10]调度方法的仿真实验结果进行对比，重点分析拓扑修剪以及流分组2 种策略在大规模调度场景下的有效性。算法性能的评价指标是求解时间与调度成功率。

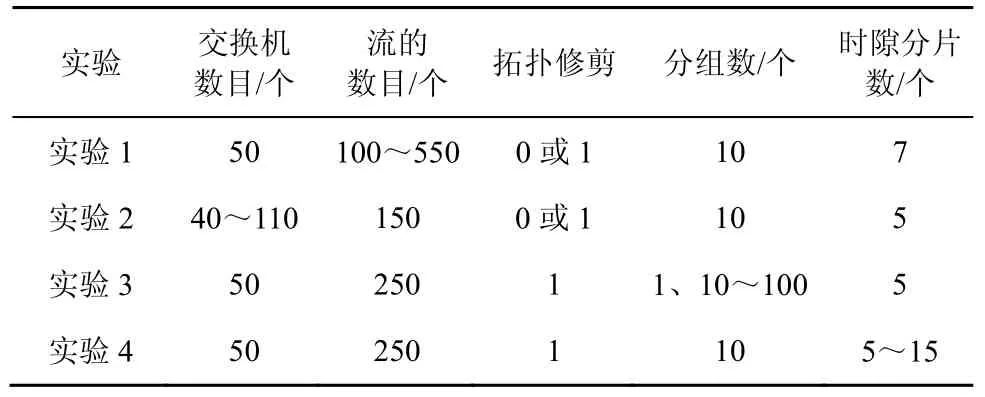
表1 仿真条件及参数的设置

4.2.1 算法随流量规模增长的表现

为了探究不同流量规模下算法性能的表现，利用表1 中实验1 的仿真条件和参数进行仿真实验，网络中交换机的数量为50 个，待调度流量的数量为100～550 个，实验结果分别如图5 和图6 所示。

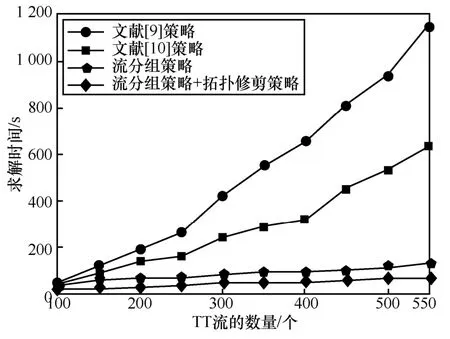
图5 求解时间随TT 流数量的变化

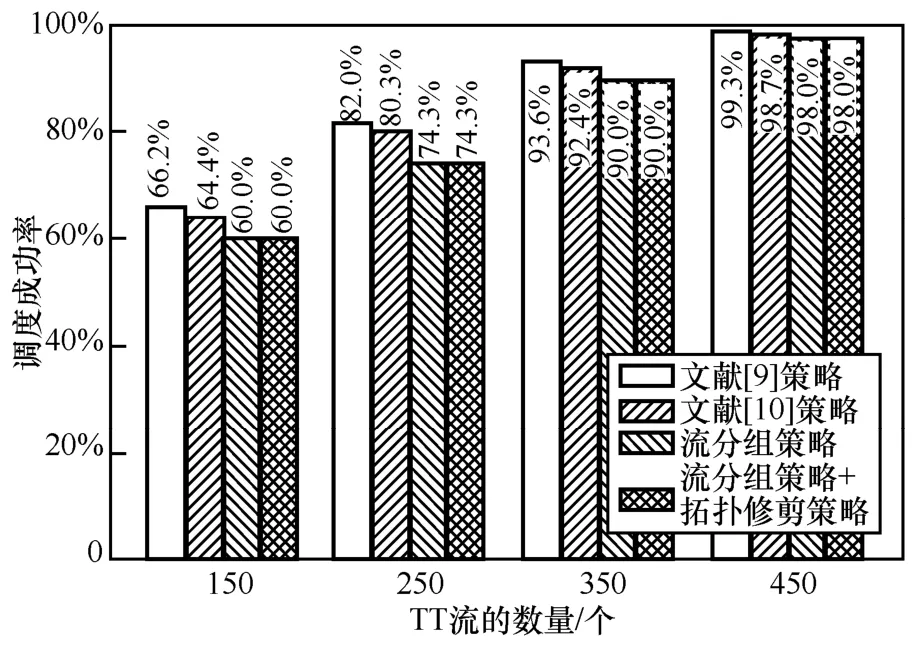
图6 调度成功率随TT 流数量的变化

由图5 可知，当采用流分组策略时，本文算法求解时间相对于文献[9-10]方法有一定下降；并且随着流量规模的增加（流量数目达到300 个以上时），求解时间降低显著。在此基础上，如果采用拓扑修剪策略，求解时间又有一定的降低。

由图6 可知，拓扑修剪策略在减少求解时间的同时，可以保证成功率不变，这与3.1 节的理论分析是一致的。对比文献[9-10]方法和采用流分组策略的结果，当待调度流量的数量为150 时，流分组策略的调度成功率与文献[9-10]方法相近。而随着待调度流量数量的增加，流分组策略会造成调度成功率出现一定程度降低，但是降低的程度是可以接受的（图6 中成功率的偏差在8%之内），同时，显著减少了求解时间。因此，综合来看分组调度机制是有效的。

4.2.2 算法随网络拓扑规模增长的表现

为了探究不同网络拓扑规模下算法性能的表现，利用表1 中实验2 的仿真条件和参数进行了仿真实验，待调度流量的数量为150，网络中交换机的数量为40～110 个，实验结果分别如图7 和图8 所示。

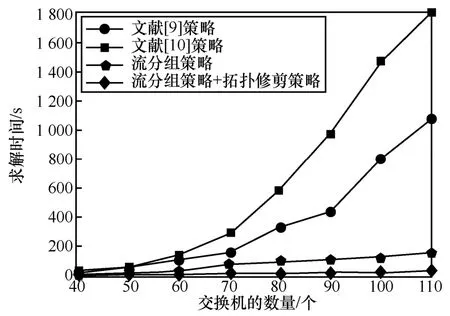
图7 求解时间随交换机数量的变化

图8 调度成功率随交换机数量的变化

几种方案的求解时间如图7 所示。当采用流分组策略时，求解时间相对于文献[9-10]方法有了一定的下降，并且随着网络拓扑规模的增加（交换机数量超过70 时），求解时间降低愈加显著。在此基础上，如果采用拓扑修剪策略，求解时间又有一定的降低。

调度成功率的结果如图8 所示。随着交换机数量的增加，可用的链路传输资源越来越多，因此各种方法的调度成功率逐渐增加。此外，通过与文献[9-10]方法的结果进行对比可以看出，随着网络拓扑规模的增加，流分组策略可以在减少求解时间的同时，保证一定的调度成功率（图8 中成功率的偏差在5%以内）。此外，对比采用拓扑修剪策略前后的结果可以看出，拓扑修剪策略在实现降低求解耗时的同时，可以保证调度成功率保持不变。

4.2.3 模型参数对于算法性能的影响

1)分组数目

通过上述实验分析，可以看出流分组策略针对大规模调度场景具有一定的有效性。为了进一步探究分组的数目对于算法性能的影响，本节利用表1 中实验3 的仿真条件和参数进行仿真实验。网络交换机数量为50，待调度流量的数量为250，分组的数量分别为一个（表示不使用流分组策略）、10～100 个，实验结果分别如图9 和图10所示。求解时间随着分组数目增加的变化曲线如图9 所示，可以看出，当分组的数量增加时，求解时间会逐渐降低，但是降低的幅度逐渐变缓。调度成功率如图10 所示，随着分组数量的增加，调度的成功率逐渐降低。

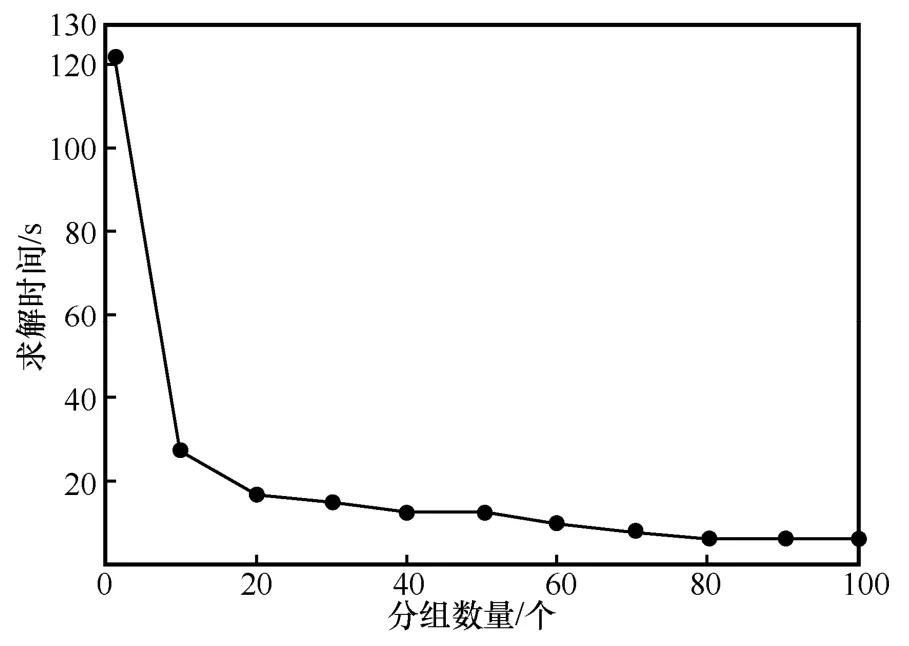
图9 求解耗时随分组数量的变化

流分组策略可以实现调度求解时间的降低，然而一直增大分组的数量也是不可取的，还应当考虑调度成功率的因素。分组数量为10 时，调度成功率为77.2%；不分组（即分组数量为1）时，调度成功率为82.8%，2 种情况下的成功率相差5%左右。随着分组数量的增加，求解时间降低的幅度逐渐变缓，但是调度成功率与不分组时成功率（82.8%）相差逐渐增大。因此，分组数目应综合考虑求解时间和调度成功率两方面因素进行选择。

图10 调度成功率随分组数量的变化

2) 基本周期的时隙分片数目

为了探究时隙分片的数目对于算法性能的影响，本节利用表1 中实验4 的仿真条件和参数进行仿真实验，网络交换机数量为50，待调度流量的数量为250，流分组的数量为10，基本周期的时隙分片数目为5～15，实验结果分别如图11 和图12 所示。求解时间随时隙分片数目增加的变化曲线如图11 所示，可以看出，随着时隙分片数目的增加，模型逐渐复杂导致求解时间逐渐增加。算法的调度成功率随时隙分片数目增加的变化曲线如图12 所示，可以看出，时隙分片的数目越多，调度成功率越高，当时隙分片的数目超过11 时，调度成功率达到100%，此时所有的待调度流量均可以在网络中传输。

图11 求解耗时随时隙分片数量的变化

时隙分片的数目代表了网络在时间维度上容纳时间触发流的能力。时隙分片的数目越多，网络中能够同时进行传输的时间触发流也越多，图12的仿真结果印证了这一点。然而，随着时隙分片数目的增加，求解时间也会增加，这是因为每增加一个时隙，模型的变量数目（即路径与时隙的映射变量）以及约束条件（即每条链路在每个时隙上的传输约束）都会线性增加，这将导致问题规模增大，从而造成求解时间的增加。此外，由于基本周期能提供的时隙分片数目是有上限的，因此时隙分片的数目应当在允许的范围内综合考虑求解时间和调度成功率两方面因素进行选择。

图12 调度成功率随时隙分片数量的变化

5 结束语

针对大规模时间敏感网络中时间触发流量的调度问题，本文提出的分组调度机制通过消除排队时延保证了时延的确定性。同时，所提拓扑修剪策略解决了由于网络拓扑规模增加而导致的求解时间剧增的问题。所提基于谱聚类的流分组策略解决了由于流量规模增加而导致的求解时间剧增的问题。仿真实验表明，该机制在大规模调度场景下可以在较短时间内求出调度结果并保证一定的调度成功率。

本文所做的工作仍有许多的不足，例如在路由策略中选择了所有最短路径的集合作为可能传输的路径集。下一步研究将综合考虑路由和调度两方面的因素来进行时间触发流量的调度研究。