双Johnson SB 分布湍流扰动OAM 光通信接收信号生成研究

陈纯毅，熊琴琴，于海洋，姚海峰，宋佳雪，娄岩

（1.长春理工大学计算机科学技术学院，吉林 长春 130022；2.长春理工大学空地激光通信技术国防重点学科实验室，吉林 长春 130022）

1 引言

光波的轨道角动量（OAM,orbital angular momentum）横向空间模为经典和量子光信息科学中的信息编码提供了一种额外的自由度，近年来受到国内外研究者的广泛关注[1-3]。在经典光通信中，人们使用OAM 来实现空间模分复用，以便提高光通信系统容量[1-2]。在光量子密钥分发领域，OAM被用于实现高维量子态，以便把超过1 bit 的信息编码在一个光子中，从而增加每个光子的密钥生成率[3]。从是否需要光缆的角度可将光通信分成光纤通信和自由空间光通信2 种形式。在这2 种形式中，前者稳定性好，但需要预先在通信双方之间铺设光缆，实施成本高；后者不需要铺设光缆，灵活机动，实施成本低，但容易受到外界环境的干扰[4]。综合比较来说，对于难以铺设光缆或者对灵活性要求很高的应用场景，自由空间光通信是一个较好的方案。

大气湍流是自由空间光通信中最重要的外界环境干扰因素之一[4-5]。为了理解自由空间光通信中大气湍流的影响，国内外学者对受大气湍流扰动的光信号的统计特性做了大量研究。目前，学者已经提出了多种描述受大气湍流扰动的光信号起伏概率分布模型，例如对数正态分布、K分布和Gamma-Gamma 分布等[6-7]。然而，这些传统分布模型在建立时没有考虑OAM 横向空间模接收的特殊性。大气湍流对OAM 光通信的影响表现为信号光功率在不同OAM 横向空间模之间的随机再分布。Chen 等[8]发现，上述光信号起伏概率分布模型不太适合用来描述因大气湍流扰动而导致的OAM接收光信号起伏，因此提出了双Johnson SB分布模型。模拟实验表明该分布模型能够很好地描述受大气湍流扰动的 OAM 接收光信号起伏统计特性。

在用蒙特卡洛方法来分析 OAM 光通信系统性能时，需要模拟生成受大气湍流扰动的OAM 接收光信号的时域随机样本。受大气湍流扰动的光信号起伏具有时间相关性，属于时域自相关信号。模拟生成受大气湍流扰动的OAM 接收光信号的关键是，要使生成的随机光信号时域样本在统计上服从双Johnson SB分布，同时具有指定的时间自相关。本文将满足这2 个条件的随机光信号称为双Johnson SB分布湍流扰动OAM 光通信自相关接收信号。文献[9-10]基于随机微分方程（SDE,stochastic differential equation）分别生成了具有指数自相关函数的Gamma-Gamma 分布和Johnson SB分布随机数序列。但目前还没有生成双Johnson SB分布湍流扰动OAM 光通信自相关接收信号时域样本的报道。文献[11]利用自回归（AR,autoregression）模型生成了具有指定时间自相关的复高斯随机样本。文献[12]利用逆变换法将自相关高斯随机样本变换为服从特定统计分布的随机样本。然而，采用逆变换法将自相关高斯样本转换为双 Johnson SB分布样本的过程较复杂。文献[13]提出的秩匹配技术通过排序操作将自相关瑞利序列的时间自相关传递给服从Nakagami 分布的白噪声随机数序列，避免了逆变换法中对目标分布的求逆运算，对生成服从双Johnson SB分布的时间自相关随机光信号的时域样本具有参考价值。

本文基于AR 模型和秩匹配法，提出一种模拟生成双Johnson SB分布湍流扰动OAM 光通信自相关接收信号的方法。所提方法分为2 个步骤：首先用AR 模型生成具有指定时间自相关的高斯随机样本；然后生成一个服从双Johnson SB分布的白噪声随机数序列，并对该白噪声随机数序列进行适当的重新排列，以匹配指定的时间自相关。其中，重排的顺序由自相关高斯过程的统计秩决定。根据指定的指数形式的时间自相关函数，本文利用所提方法生成了双Johnson SB分布湍流扰动OAM 光通信接收信号，并将生成信号的自相关系数与理论自相关系数的均方误差作为生成信号的自相关性匹配精度，由此分析了不同的双Johnson SB分布模型参数对OAM接收光信号时域样本的自相关性匹配精度的影响。

2 OAM 光通信湍流扰动接收信号模拟模型

生成自相关高斯随机数序列的常用方法为采用线性滤波，高斯白噪声随机数序列经过线性滤波后可获得指定的自相关，并且服从其原有的高斯分布[11]。当目标分布为非高斯分布时，仅进行线性滤波不再可行，例如，对指数序列进行线性滤波时，输出的自相关随机数序列将不再服从指数分布。对于双Johnson SB分布来说，这个结论同样适用。为了对双Johnson SB分布湍流扰动OAM 光通信自相关接收信号进行蒙特卡洛模拟，本文提出如图1 所示的原理框架。首先使用AR 模型生成具有指定自相关的高斯随机信号，将其作为辅助集；然后利用蒙特卡洛接受−拒绝采样法[15]生成服从双Johnson SB分布的白噪声随机信号，即样本集；最后通过秩匹配将样本集按照辅助集的统计秩进行重新排列，在不改变分布特性的情况下使样本集具有指定的自相关。

2.1 基于AR 模型的自相关高斯过程

AR 模型本质上是一种线性滤波器，能生成具有指定自相关的高斯随机过程。由文献[9]可知，指数形式的归一化时间自相关函数如式(1)所示。

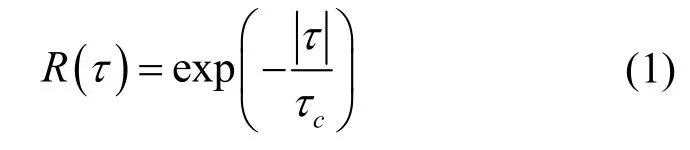
其中，τ表示时延，τc表示时间自相关长度。基于AR模型生成的自相关高斯过程称为AR高斯过程，一个p阶AR高斯过程通过时域递归[11]表示为

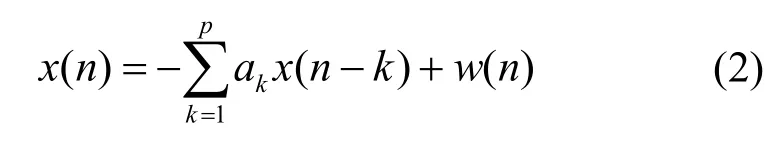
其中，ak(k=1,2,…,p)表示AR 模型系数，p表示AR 模型的阶数；w(n)表示高斯白噪声信号，其均值为0、方差为。AR 模型的参数包括系数ak和高斯白噪声的方差，它们和指定的自相关序列R(n)间的非线性关系用Yule-Walker方程[14]可表示为

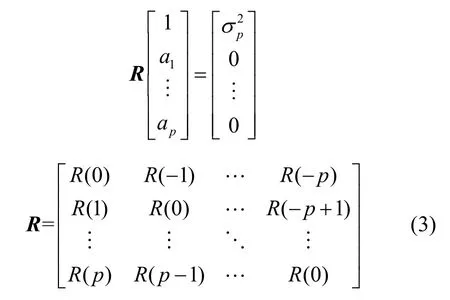
其中，R表示由R(n)构成的自相关矩阵，R(n)表示式(1)对应的自相关值序列，具体为

其中，Δt表示采样时间间隔；对于本文的p阶AR高斯过程，n满足−p≤n≤p的条件。

本文利用Levinson-Durbin 递推算法来快速地求解式(3)，得到AR 模型的参数。该算法的初始值[14]为

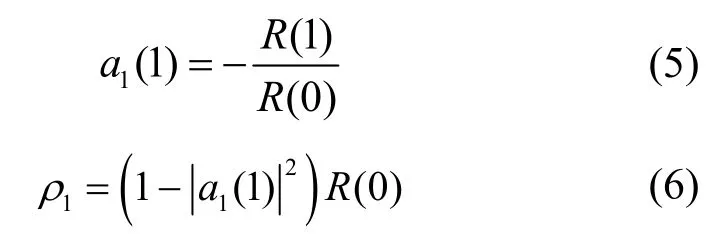
对于k=2,3,…,p，递推写为[14]

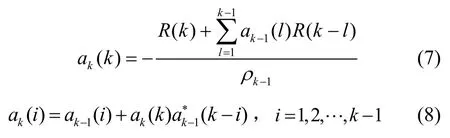
其中，

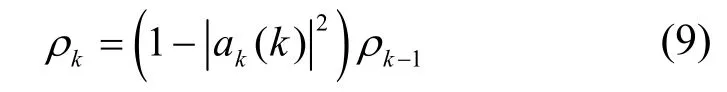
其中，ρk为k阶预测误差方差。递推完成得到参数集{a1(1),ρ1},{a2(1),a2(2),ρ2},…,{ap(1),ap(2),…,ap(p),ρp}。最后的p阶参数集就是Yule-Walker方程的解，即ap(i)=ai,i=1,2,…,p，。对式(4)的自相关序列进行一次Levinson-Durbin 递推后，式(9)中的预测误差方差便不再随p的增加而变化，由此确定AR 模型的阶数p为1。

由式(2)可以看出，若要得到x(n)，除了AR 模型的参数外，还需要计算前p个平稳输入序列元素的初始值[11]。对于本文的一阶AR 模型，其初始条件x(0)是均值为0、方差为1 的高斯变量。最后将AR 模型的参数和初始条件代入式(2)，就得到自相关高斯过程。

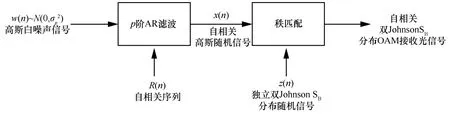
图1 本文的原理框架

2.2 自相关双Johnson SB 分布接收光信号

由自相关高斯过程生成自相关非高斯过程的标准方法是非线性逆变换法[12]。在这种方法中，目标分布的累积分布函数（CDF,cumulative distribution function）非常重要，因为在构建合适的非线性变换和高斯过程的自相关函数时都需要目标CDF的反函数。对双Johnson SB分布来说，其概率密度函数比较复杂，不便于获得其CDF 的反函数，因此本文不考虑使用该方法而是利用统计秩来匹配指定自相关[13]。

统计秩是按指定（递减或递增）顺序排列的样本列表中一个值的序数[13]，本文选择升序排序。假设样本长度为5，对应的统计秩向量如图2 所示，其中，第i个元素表示排列中第i个原始样本的统计秩。对于平稳随机过程，样本的自相关函数近似于其统计秩的自相关函数[13]。因此，AR 高斯过程和双Johnson SB分布随机过程具有式(10)所示关系。

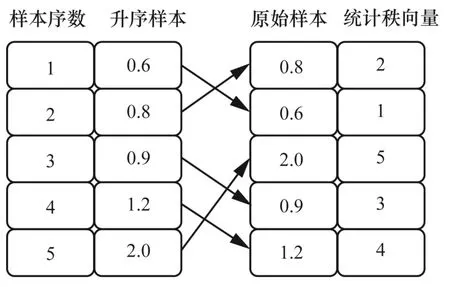
图2 统计秩向量原理

其中，RGau和分别表示AR 高斯过程及其统计秩的自相关函数；RJoh和分别表示双Johnson SB分布随机过程及其统计秩的自相关函数。若双Johnson SB分布随机过程的统计秩与AR 高斯过程的统计秩相同，则二者统计秩的自相关函数相同，为

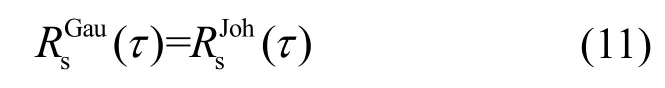
由式(10)和式(11)可得

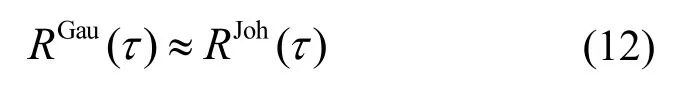
由此可知，将服从双Johnson SB分布的样本按照AR 高斯过程的统计秩进行重排，可以得到与AR高斯过程秩匹配的自相关双Johnson SB分布随机过程，实现过程如图3 所示，具体步骤如下。

步骤1生成服从双Johnson SB分布的白噪声随机信号。双Johnson SB分布的概率密度函数（PDF,probability density function）为[8]

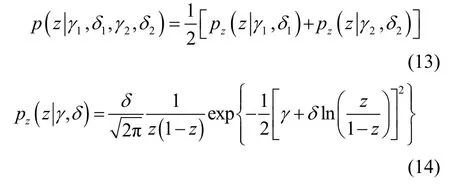
其中，4 个模型参数满足条件δ1＞0，δ2＞0，γ1≤γ2；pz(·)表示Johnson SB分布的PDF。为了避免数值拟合双Johnson SB分布CDF 的反函数，本文采用蒙特卡洛接受−拒绝采样法[15]生成服从双Johnson SB分布的白噪声随机信号，计算方法 如下。

1)分别生成在[c,d]和[0,1]范围内均匀分布的随机变量u和v。

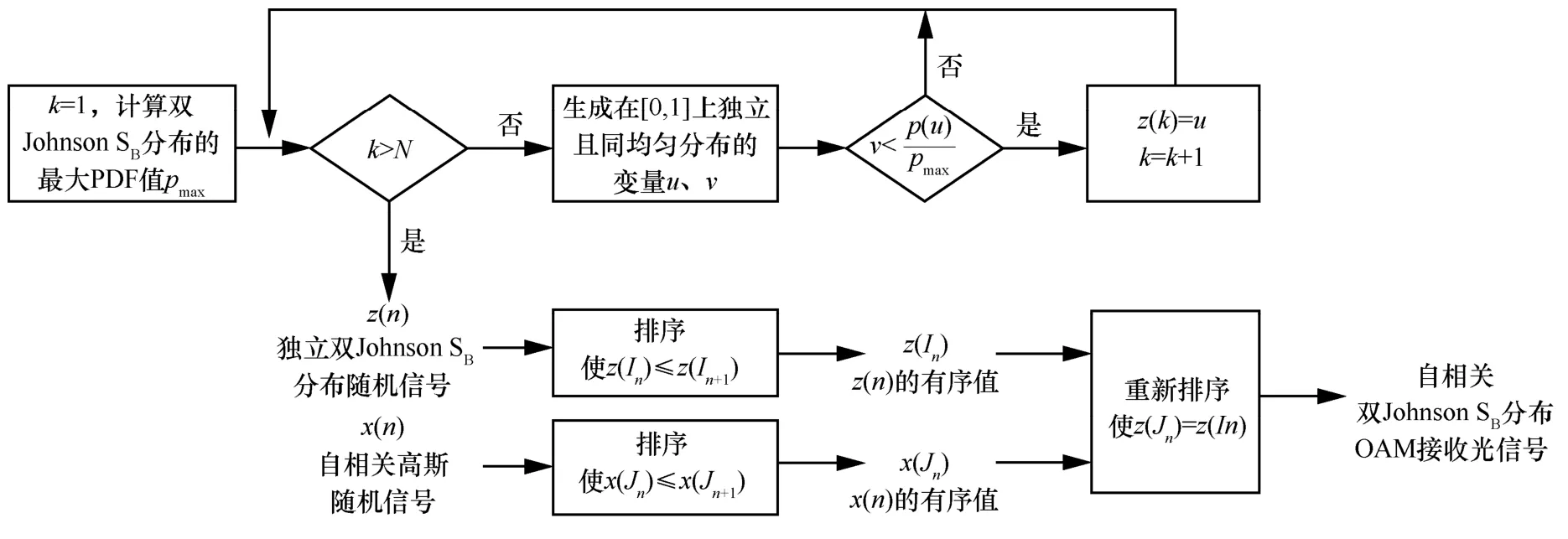
图3 双Johnson SB 分布湍流扰动OAM 光通信自相关接收信号的秩匹配流程

3)重复1)和2)，直到生成N个被接受样本，其中，N表示样本长度。

步骤2找到自相关高斯随机信号x(n)的统计秩向量。由图2 可以看出，原始样本的统计秩向量与其进行递增排序后的索引向量相同。因此，对x(n)升序排序，得到x(Jn),n=0,…,N−1，其中索引Jn使x(J0)≤x(J1)≤…≤x(JN−1)，Jn即为x(n)的统计秩向量。

步骤3根据Jn对双Johnson SB分布白噪声随机信号z(n)进行重新排列，使z(n)的最小值放置在与x(n) 最小值相同的位置，z(n)的第二小值位于x(n) 第二小值的位置，以此类推。首先将z(n)升序排序，使z(I0)≤z(I1)≤…≤z(IN−1)，有序值记为z(In),n=0,…,N−1；然后重排z(n)，即

最后得到的重排信号z(n) 就具有指定的时间自相关并且服从双Johnson SB分布。

3 仿真实验与讨论

通过模拟仿真实验来验证图1 所示的原理框架，所有仿真的样本长度N=105、采样时间间隔Δt=0.1 ms。为了更准确地描述双Johnson SB分布OAM 光通信接收信号的自相关性，所有仿真实验重复100 次，并根据这100 次仿真得到的数据来计算自相关系数。

图4(a)为τc=10 ms、δ1=3、γ1=1.1、δ2=5、γ2=2.4的双Johnson SB分布湍流扰动OAM 光通信自相关接收信号，其中，双Johnson SB分布的4 个模型参数的取值源自文献[8]。图4(b)为对应仿真信号的自相关系数随时延变化的曲线，与式(1)的理论归一化自相关函数基本一致。为了进一步分析仿真信号的自相关性是否与理论值匹配，本文以仿真信号的自相关系数与理论自相关系数的均方误差（MSE,mean square error）作为自相关性匹配精度，即

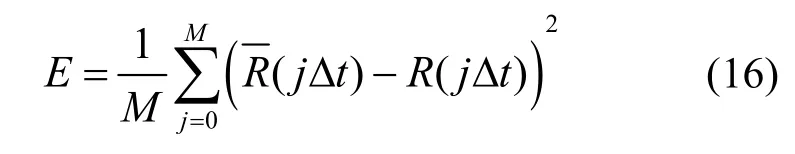
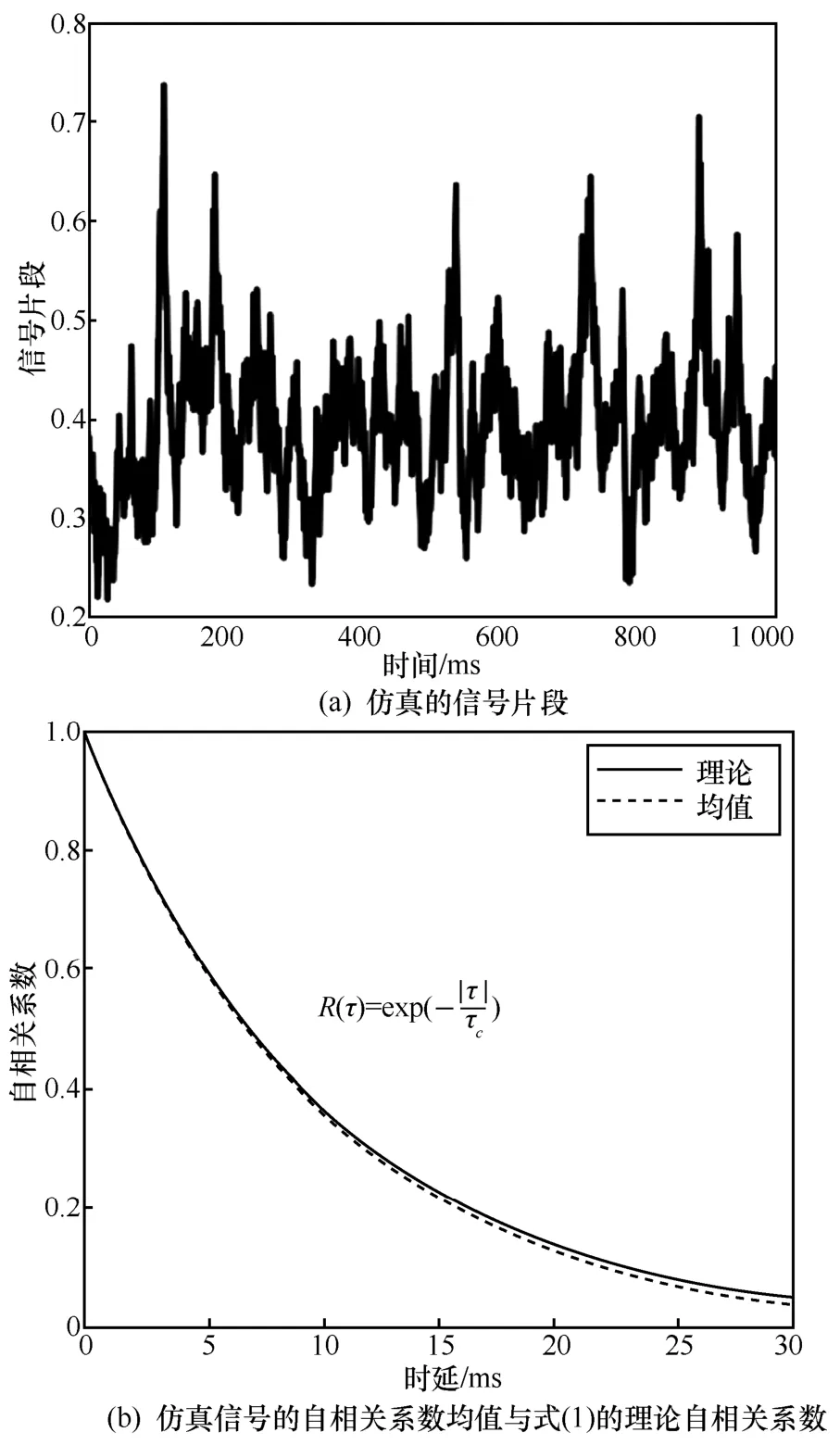
图4 双Johnson SB 分布OAM 光通信接收信号及其自相关函数示例

为了验证所提方法的有效性，根据文献[8]提供的查找表，另外设置了6 组双Johnson SB分布的模型参数进行仿真实验，如表1 所示。当τc=10ms 时，根据表1 的参数仿真生成信号的概率密度如图5所示。OAM 功率传输系数为接收的特定OAM 模中的功率与特定OAM 模的发射功率之比[8]。本文通过生成的双Johnson SB分布湍流扰动OAM 光通信自相关信号对应的功率传输系数扰动来表征OAM光信号功率接收时域扰动。

表1 6 组双Johnson SB 分布模型参数值

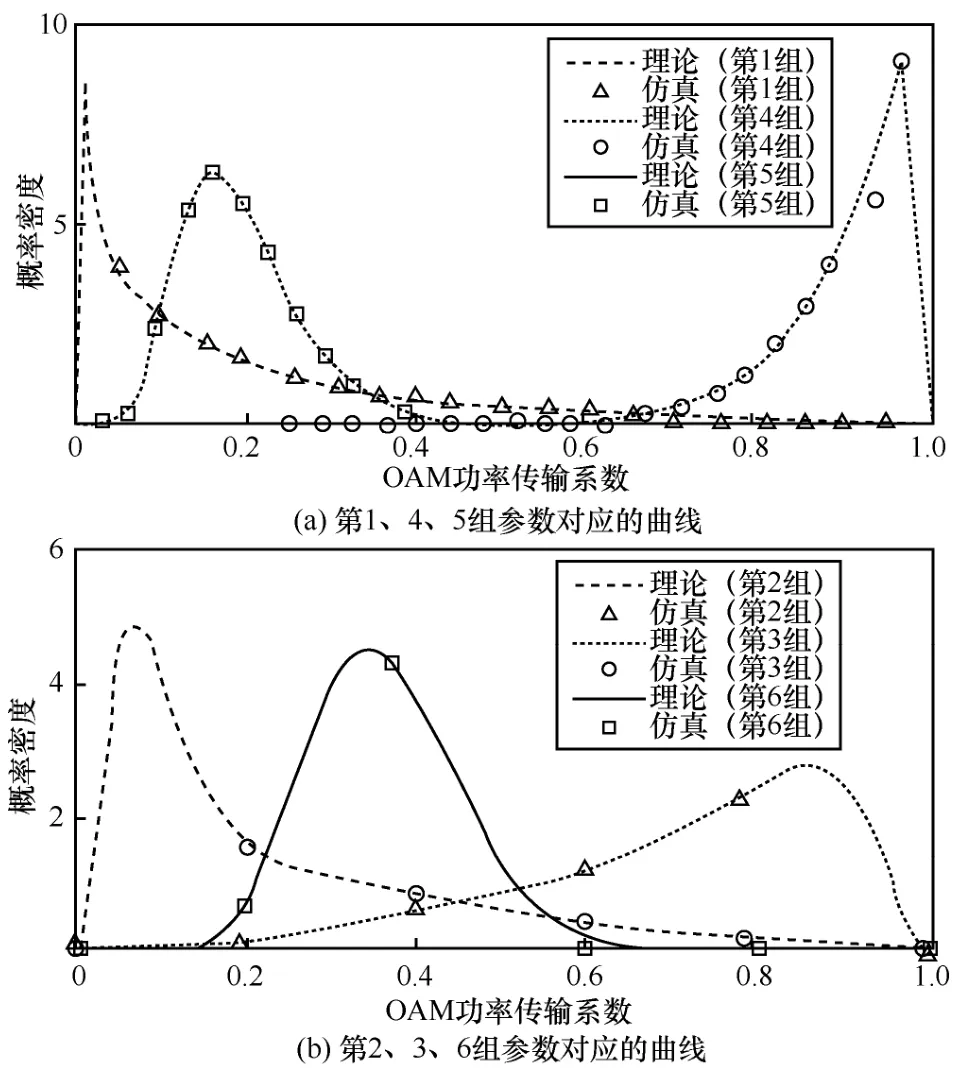
图5 根据表1 的参数仿真生成信号的样本概率密度与理论概率密度的对比(τ c=10ms)

图6 表示当τc为10 ms 和20 ms 时，根据表1的参数仿真生成信号的自相关系数与理论自相关系数。从图6 可以看出，仿真信号的自相关性基本匹配理论自相关性。当双Johnson SB分布的形状与高斯分布比较相似时，误差会减小。通过式(16)的自相关性匹配精度对此进行详细分析，M的取值如图4 所示。

表1 中模型参数对应的匹配精度如表2 所示。从表2 可以看出，τc=10 ms 时的匹配精度与τc=20 ms 时的精度基本上接近。其中第4 组和第6 组参数的匹配精度最好，结合图5 的概率密度曲线可以看出，这是由于第4 组和第6 组模型参数对应的概率密度曲线形状类似于高斯分布。值得注意的是，AR 模型的输出是均值为0、方差为1 的自相关高斯过程。进一步分析可知，当进行秩匹配的2 种分布相似时，本文所提方法的仿真精度更高。

为分析双Johnson SB分布的模型参数值对仿真信号的自相关性的影响，对表2 进一步研究：将第1 组参数与第6 组参数的自相关性匹配精度进行比较可以看出，随着δ1和δ2的增加，接近或者大于2 时，自相关性匹配更好；根据第6 组参数的匹配精度优于第4 组参数的精度和第2 组参数的匹配精度优于第5 组参数的精度可以发现，当越小时，自相关性匹配越好；通过对比第3 组与第5 组的匹配精度发现，当的比率接近于1 时，匹配精度更高。对于表2 中的6 组双JohnsonSB分布的模型参数，对应的自相关性匹配精度基本保持在10−3以下，再次说明了所提的双Johnson SB分布湍流扰动OAM 光通信自相关接收信号蒙特卡洛模拟方法的有效性。该方法生成的信号可用于研究大气湍流对OAM 光通信的影响。

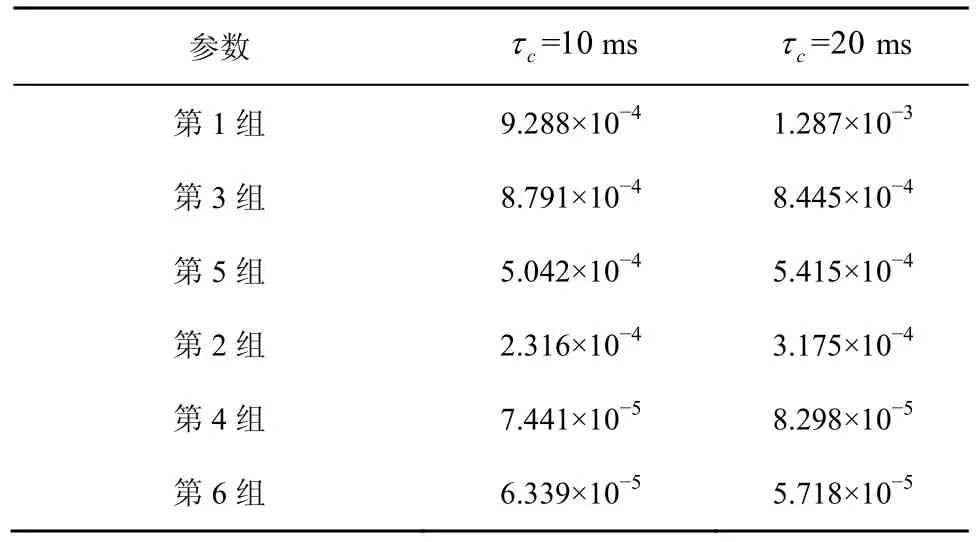
表2 表1 的6 组模型参数的自相关性匹配精度

4 结束语

本文提出一种基于AR 模型和秩匹配的双Johnson SB分布湍流扰动OAM 光通信自相关接收信号蒙特卡洛模拟方法。由于AR 模型的参数计算简单，秩匹配法仅涉及排序，因此本文所提方法具有复杂度低、便于工程应用的优点。通过模拟仿真实验发现，模拟生成的信号在统计上满足双Johnson SB分布且具有指定的时间自相关，进而证明了本文所提方法的可靠性。本文所提方法生成的双Johnson SB分布湍流扰动OAM 光通信自相关接收信号，可以为用蒙特卡洛方法分析大气OAM 光通信系统性能提供支持。

图6 不同条件下的仿真生成信号自相关函数与理论自相关函数的对比