基于蚁群算法的骨干网络发现

吕芳，柏军，黄俊恒，王佰玲

（1.哈尔滨工业大学（威海）计算机科学与技术学院，山东 威海 264209；2.哈尔滨工业大学（威海）网络空间安全研究院，山东 威海 264209）

1 引言

信息交互网络指由实体之间信息的流通构建的有向网络结构，例如电话网络、金融网络、路由网络、交通网络等。此类网络与社交网络的显著不同在于，后者中边的存在表示其连接的实体之间存在相似性关系，而前者中的边只依赖于实体之间的信息交互需求，不具有传递性和相似性。以金融网络为例，其中庞大、繁杂的交互关系，是真实社会中个人、组织进行有目的的经济活动的产物。研究交互网络中实时动态的交互关系，对分析网络结构背后的组织活动有直接的指导意义，多年来引起了研究者的广泛关注[1-2]。目前，针对金融网络中交互路径的研究可归为以下3 类：辅助表示节点特征[3-4]、检测异常交互路径[5-6]和可疑关系分析与预测[7-8]。上述研究集中于解决动态[3,5]、稀疏[8]的金融网络中异常节点和异常边的识别。由于金融网络数据中的噪声、冗余信息明显，上述算法的设计均需要在一定程度上考虑算法的稳健性。如何抽取出能够反映真实交互关系的核心网络，为研究人员提供一个相对纯净、可靠的骨干网络，是本文关注的核心。

为解决上述问题，本文提出模拟信息交互在时空上呈现的交互路径，即发现核心流通轨迹，以实现骨干网络的提取。核心流通轨迹发现可抽象为网络中的最优路径选择，属于组合优化问题。路径寻优是一类NP-hard 问题，长期以来都是研究者的关注热点。给定有向图G=(V,E)，若V中节点的平均出度为d，则G中长度为的路径总个数约为条，可见路径条数随l呈指数增长。当G的规模变大，使用传统算法解决此类问题的计算成本将无法承受。近年来，众多研究发现仿生智能算法在解决组合优化问题时体现出了良好的性能，为很多NPC（non-deterministic polynomial complete）问题的求解提供了新的思路和解决方案。其中，蚁群算法（ACA,ant colony algorithm）[9]是一种可用来解决路径优化问题的概率型智能仿生优化算法。作为一种启发式全局优化算法，ACA 不依赖于严格的数学定义，而是利用信息反馈机制进行启发式搜索，具有较强的稳健性和并行性[10]，在解决复杂优化问题方面有着很好的性能。ACA 的研究应用从最初的旅行商问题（TSP,traveling salesman problem）[10]逐渐拓展到了路径规划、车间作业调度、图像处理等很多领域。特别地，在图结构的路径寻优问题上，搜索蚂蚁系统（GBAS,graph-based ant system）[11]最早证明了ACA 在图结构上进行路径寻优的合理性。GBAS 将图上的可行路径视为优化目标的最优解，实现了蚁群模型向图结构路径寻优问题的迁移，此后涌现出一系列针对图分析领域不同应用的蚁群优化模型[12]。

金融网络利用实体间的交互关系，由真实的交互信息流数据构建得到，具有复杂网络特点的图结构[6]。交互实体可抽象为节点，实体间的有向交互关系抽象为节点间的有向边，实体间的交互信息量、交互频次等信息表示有向边的权重。图1 为由真实金融流通日志数据构建的局部网络示意，其中边的箭头方向为交互信息的流通方向。

图1 金融局部网络示意

真实的信息交互网络具有如下特点：节点规模庞大，节点之间的路径不止一条且存在环路，且节点的度分布差异性较大。网络中存在着少数的活跃节点，其度、交互频次均显著高于其他节点。这些活跃节点处于交互网络中的关键位置，对网络的连通性有着重大的影响。此外，交互网络的边会随着时间的改变而发生变化。本文将其简化为静态网络，将在一定时间周期内存在有序交互活动的连续流通路径视为有效运行轨迹。核心流通轨迹在时间上具有一定的规律性，且往往流通了网络中的大部分信息，因此可以反映一定时间内信息的主要活动与分布。以图1 中的实际金融网络为例，其核心流通轨迹如图2 所示。可见，金融网络中有向边的双向流通权重不等价；网络规模较大且稀疏；两实体间的最优交互路径不止一条且存在环路。为了实现利用蚁群路径选择模拟信息流通，利用蚁群信息素更新标识路径的重要性，本文提出了一种蚁群模型FNT-Ant，该模型对传统蚁群模型做了如下改进。

1)根据网络中心性理论，改进了蚂蚁初始位置的选择策略，以保持节点的重要性与选中概率一致。

2)设计了一种适用于发现核心流通轨迹的蚁群路径选择机制，以模拟网络中的信息流通行为。

3)借鉴GBAS 思想，制定了一种动态自适应的信息素更新策略，以保证模拟过程收敛。

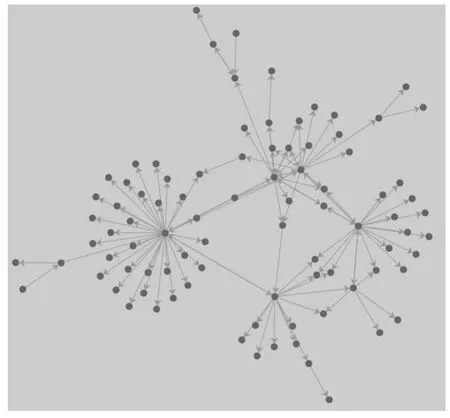
图2 核心流通轨迹示意

本文提出的FNT-Ant 算法相对传统蚁群算法收敛速度更快，解的性能更好。在真实数据上的实验结果表明，FNT-Ant 算法提取的骨干网络覆盖了65.57%的网络关键节点。这一结果优于传统算法，证明了FNT-Ant 算法优化思想的合理性，简化了后续在信息交互网络中的异常检测、可疑路径分析等任务。

2 相关工作

在金融网络中，核心流通轨迹发现的研究尚处于初级阶段，从网络理论上来说，其与骨干网络发现属于相近的研究范畴。

Chawla 等[13]在对交通网络进行骨干网络发现时，采用贪心算法和基于原始对偶的算法，考虑到边的中介中心性和通勤时间中心性，引入伸缩因子的概念，然后将其定义为加权调和平均数对算法进行优化。文献[13]的优化目标与本文要解决的问题类似，也是要找出网络中的主干路径。但是，文献[13]中的交通网络图数据规模较小且节点的空间分布位置固定，而信息交互网络的数据集规模庞大，网络节点相对位置不固定，边具有方向性，网络中存在环路且信息流通轨迹不止一条。此外，随着网络规模的扩大，网络结构愈发复杂，轨迹发现的难度也随之大大增加，这使传统算法难以求解。Katsikouli 等[14]在研究分布式道路系统时采用了一种随机抽样算法进行频繁的路径挖掘，其在保证算法准确性的基础上，大大提高了相对确定性算法的运算效率，证明了随机算法的高效性和准确性。该问题和本文交互网络中核心流通轨迹发现问题均为NP-hard 问题，其解决方法为本文提供了思路。

蚁群算法作为随机算法的一种，综合了贪心算法和概率的思想，既弥补了贪心算法容易陷入局部最优的不足，又通过概率反映了不同解的最优程度。因此，蚁群算法常被广泛应用于解决路径规划相关的优化问题，如车辆路径规划[15]、数据挖掘[16]、网络路由[17]、图像处理[18]、机器人路径规划[19]等。蚁群算法是一种通过模拟自然界真实蚂蚁的群体行为来寻求问题最优解的仿生优化算法。它的基本模型最早是在1991 年由Colorni 等[20]提出，此后结合实际应用问题的优化方案层出不穷[9]，如Gambaedella 等[21]提出的Ant-Q System 和Gutjahr[11]提出的基于图的蚁群系统（GBAS,graph-based ant system）。Gutjahr[11]首次对蚁群算法的收敛性进行了证明，随后将其应用于图结构中的路径寻优。他将图中的可行路径视为蚁群系统在图结构中路径优化问题的可行解。Gutjahr[11]还提出了图中边、全局路径上信息素的累积和挥发策略，之后又相继提出了GBAS/tdev 和GBAS/tdlb 算法[12]。他的研究证明了通过改变信息素的挥发因子或给信息素设置下界可加快算法收敛到最优解的速度。为了避免寻优过程的过早停滞，Stuetzle 等[22]改进了信息素更新策略，提出了最大−最小蚂蚁系统（MMAS,max-min ant system）。MMAS 只更新本次迭代最优路径上的信息素，并通过设置边上信息素浓度的上下限来避免寻优过程过早停滞。近年来，我国学者对蚁群算法也做了大量的研究[23-25]。在理论方面，段海滨等[23]利用Markov 链和离散熵对信息素轨迹向量的收敛性进行了理论证明，给出了基本蚁群算法首达时间的定义及其理论分析；杨佳等[24]提出了一种新的量子蚁群优化算法，结合量子计算理论、进化计算理论和蚁群算法解决连续空间的优化问题。在算法优化方面，朱庆保等[25]提出了一种基于变异策略，采用最近邻居节点选择原则并对信息素进行动态更新的蚁群优化算法，大大提高了蚁群算法的收敛速度，该算法可用于解决大规模优化问题等。蚁群模型在图结构上路径寻优的研究，为本文利用基本蚁群模型解决流通路径寻优问题提供了理论依据和实验指导。

为了说明蚁群算法对路径寻优的原理，本节对其原理进行简要介绍。蚁群算法最早成功应用于TSP[10]问题中。下面，以TSP 为例，对传统蚁群算法的数学模型进行描述。设TSP 问题中的城市规模为n，蚂蚁的总数目为m，任意t时刻城市i中蚂蚁的数目为bi(t)，则

在初始时刻，将各路径上信息素浓度设为定值tij(0)，其中，tij(t)为t时刻路径(i,j)上的信息素浓度。在蚂蚁行走过程中，使用禁忌表tabu 依次记录蚂蚁k(k=1,2,…,m)走过的城市，并随蚂蚁的迭代过程对tabu 进行动态更新。现有针对蚁群算法的研究核心为路径选择机制和信息素调节机制，对其介绍如下。

1)路径选择机制

路径选择机制是蚂蚁在转移过程中根据当前路径上信息素的浓度来决定下一步要到达的城市。蚂蚁k的路径选择可使用状态转移概率获得，则在t时刻蚂蚁k由节点i转移到节点j的状态转移概率为

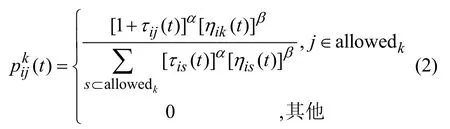
其中，allowedk={C−tabuk}为k下一步允许选择的城市集合；α为信息素启发因子，用来表示信息素积累项的重要度；ηik(t)为t时刻路径(i,k)的期望启发函数，反映了蚂蚁从城市i到k的期望程度，为城市(i,k)间的距离；β为期望启发因子，表示信息素能见度项的重要度，β取值越大，蚂蚁的路径选择策略越接近于贪心。

2) 信息素调节机制

为了避免因为路径上的信息素过多而削弱启发信息的作用，蚁群算法需要对路径上的信息素进行更新，更新方法主要有2 种：一种是局部更新，即蚂蚁每走完一步就利用局部信息对路径上的信息素进行更新；另一种是全局更新，即蚂蚁在完成一个循环后利用整体信息对所有路径上的信息素进行更新。根据信息素积累和挥发规则，调节路径上的信息素浓度。用表示本次循环结束时第k只蚂蚁在路径(i,j)上信息素的增量，τij(t+1)表示t+1 时刻路径(i,j)上的信息素总量，两者分别按照式(3)和式(4)进行更新。

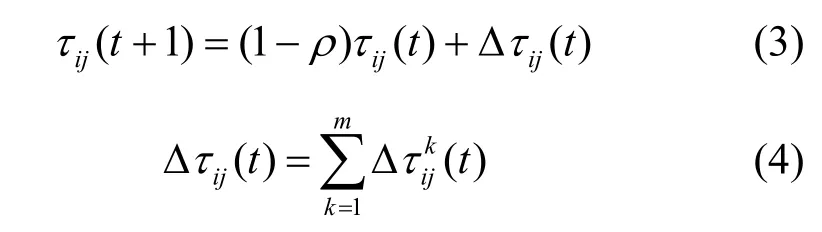
其中，ρ为信息素挥发因子，1−ρ为信息素残留系数。根据信息素的更新策略不同，Colorni 等[20]提出了 3 种不同的基本蚁群算法模型，分别为Ant-Quantity 模型、Ant-Density 模型和Ant-Cycle模型，这3 种模型的差别在于的计算方法。Ant-Quantity 模型和Ant-Density 模型采用的是信息素局部更新，而Ant-Cycle 模型采用的是信息素全局更新，具体计算式为

其中，Q和Lk分别表示信息素强度和第k只蚂蚁在本次循环过程中所走路径的总长度。相较另外2 种模型，Ant-Cycle 模型在求解TSP 问题时性能更好，因此该模型被视为蚁群算法的基本模型。

3 FNT-Ant 算法

在传统蚁群算法的理论基础上，本文根据信息交互关系的特点，设计了一种适用于发现交互网络中核心流通轨迹的FNT-Ant 算法。FNT-Ant 算法引入网络中心性设置蚂蚁初始点，设计了符合信息流通特点的路径选择机制，制定了自适应的信息素动态更新策略，有效地将传统蚁群算法迁移到了交互网络路径寻优问题中。下面，将首先给出问题定义，然后详细介绍FNT-Ant 算法的具体构建方法。

3.1 问题定义

实体之间的动态流通数据体现了复杂的信息交互关系，可构建成有向加权时序交互网络。交互实体抽象为网络节点，实体之间的交互关系抽象为网络中的有向边，实体之间的交互信息量、频次特征作为有向边的权重。有向加权时序交互网络的定义如下。

定义1信息交互网络。一个信息交互网络可表示为G=（V,E,W），其中，V={v1,v2,…,vn}为节点集合；E={eij=＜vi,vj＞|vi,vj∈V,vi对vj至少有一次交互}⊂V×V为边集合。W={wij|eij∈E,1 ≤i,j≤n},，wij={(t(1)ij,r(1)ij),(t(2)ij,r(2)ij),…,(t(Nij)ij,r(Nij)ij)}，其中，t(k)ij、r(k)ij分别表示节点vi向vj的第k次交互时间、信息量，Nij表示vi向vj的总交互次数。

G中边的权重反映了节点的关系强度，eij流通的信息量越大，交互越频繁，说明vi对vj的联系越紧密，影响作用越强。因此，利用交互信息量和频次这2 个因子度量边eij的权重，如式(6)所示。

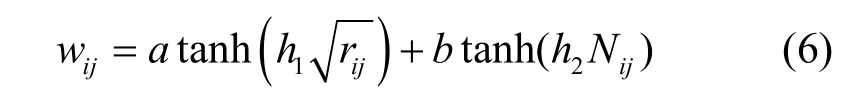
其中，a、b=1−a分别表示信息量、频次所占的权重，h1、h2分别表示对应系数。wij采用模糊集合论中隶属度的思想，对两因子进行规范化，即利用tanh 函数构造隶属度函数，以缩小权值之间的差异。本文交互网络中的骨干网络定义如下。

定义2骨干网络。给定G=（V,E,W），若存在子网络H=(V′,E′,W′)，满足

则称子网络H为G的骨干网络，其中，分别为集合W和W′中元素的个数，M和K为阈值。

核心流通轨迹可反映出交互网络中信息的主要流向，表现在全局交互网络中即为网络的主干路径。核心流通轨迹发现问题可抽象为从交互网络G中抽取出主干路径构成骨干网络H。

3.2 FNT-Ant 蚁群模型

在蚁群算法中，蚂蚁初始位置的选择和信息素的更新策略对算法的收敛速度和解的质量有很大影响，而蚂蚁的路径选择机制则需要依据具体的问题进行设置。下面，针对FNT-Ant 蚁群模型中蚂蚁初始位置的选择、路径选择机制的设置和自适应的信息素动态更新策略进行详细阐述。

3.2.1 蚂蚁初始位置的选择

传统蚁群算法在解决TSP 问题时，蚂蚁的初始位置是随机放置的，这在处理TSP 问题时是可行的，原因在于：1) 在求解TSP 问题时，要求每只蚂蚁遍历所有节点，该过程构造出来的所有路径均为问题的可行解；2)算法优化目标为找到一个最优解。然而上述思路难以直接迁移到文本问题中，因为：1)交互网络规模庞大节点众多，遍历网络中的所有节点难以实现；2) 优化目标为最优信息流通路径集合，即每只蚂蚁所找到的路径可能只是最优解的一部分。在蚁群算法中，初始位置的选择对算法执行的效率和求解的性能均有着很大的影响。4.3 节将蚁群初始位置随机设置和本文对初始位置的改进进行了对比实验，对比分析发现，随机放置蚂蚁时得到的解的性能较差，算法容易出现早熟停滞现象。由此可见，随机放置蚂蚁在本文问题中显然是不可行的。因此，本文基于交互网络的特点以及复杂网络中的节点中心性理论[26]，改进了初始位置选择策略，其中对网络中处于关键位置的节点给予了更多的关注。

网络中节点的重要程度可以通过节点的中心性来进行评价[27]，包括节点的度中心性、介数中心性等。节点的度中心性[28]是节点中心性最直接的度量指标。节点i的度中心性DCi为

其中，ki为节点i在网络中的连边数，n为网络中的节点数目，n−1为节点可能的最大度值。DCi通过节点邻居数量多少来反映节点的影响力大小，也就是说节点的度越大，它的重要性也就越大。可见，节点的度中心性是网络局部特性的重要评价指标。

节点的介数中心性[29]指图中经过该节点的所有最短路径的比重。节点i的度中心性BCi为

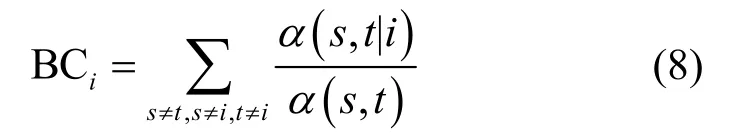
其中，α(s,t)表示节点s到节点t的最短路径数目，α(s,t|i)表示节点s到节点t的最短路径中经过节点i的数目。可见，BCi反映了网络的全局特性。

对于节点i来说，DCi和BCi这2 个指标评价依据不同且各有侧重，为了避免单一指标评价过于片面，本文综合两者对节点i的重要性进行度量，具体计算式为

其中，k1和k2为比例系数，且k1+k2=1。G中V的节点重要性总和为SP，本文使用轮盘赌方式为蚂蚁选择起始位置，节点i的选择概率为

本文中蚂蚁初始位置的选择对网络中的重要节点给予了更多关注，增大了网络中重要节点作为蚂蚁起始节点的概率，提高了算法的收敛速度和求解质量。

3.2.2 路径选择机制的设置

以金融网络为例，交互日志数据中包含的信息有原账号、对手账号、金额、频次等，部分数据如表1 所示，其中权值项由式(6)得到。

表1 金融网络日志记录数据示例

蚁群算法的优化目标与实际应用问题直接相关，在解决不同的问题时需要构建不同的目标函数。例如，TSP 问题的目标函数是路径长度和最小[30]；车辆路径规划问题的目标函数是汽车总的行驶路程最短和车辆数目最少[31]；图像处理的目标函数是蚂蚁与聚类中心的相似度最大[32]。本文问题与其他同类问题对比如表2 所示，可见研究问题都属于组合优化问题中的路径优化问题，但是数据类型以及规模不同，优化目标不同。

蚂蚁在选择路径的过程中，目标函数会通过一系列约束条件来不断调整蚂蚁的前进方向，将优化方向向着最优方向引导。本文所解决的问题相对较复杂，作为优化目标的核心流通轨迹要能体现出在整个网络中信息的主要流动方向，这就需要通过对具体的实验数据进行分析来构造出合适的目标函数。基于定义1，本文的优化目标为网络中的核心流通轨迹整体权重之和占据网络总权重的比重尽量大，且轨迹中每条边的权重尽量大，能够表现出信息的主要流动方向。据此，本文设计的目标函数如下。

表2 本文问题与其他同类问题对比

设路径为Γ=v1,v2,…,vl−1,vl,vl+1，路径上的边权重为wij,1≤i＜j≤l+1，设计的目标函数为

其中，fk(t)为第t代第k只蚂蚁走过路径的目标函数，lk(t)为此蚂蚁走过的路径长度，ωij为蚂蚁走过边的权值。蚂蚁从节点的邻居集合中选择一个节点u，计算此时的fl+u，若fl+u＞fl，则选中该有向边为转移路径，反之则排除该节点，重新进行路径选择，直到无边可选。当一只蚂蚁停止，即可得到一条局部最优路径；一代蚂蚁走完之后，得到本代的最优路径集合及其目标函数值之和。表1 中日志数据交互关系如图3 所示。具体地，图3 中最优路径集合的目标函数之和计算过程如下。

图3 表1 中数据的交互关系

假设蚂蚁当前已经走过的路径为a→b→c，则fac为

若选择边(c,d)，则fad为

由于fad＜fac，则放弃边(c,d)，尝试走(c,e)，则fae为

此时，fae＞fac，则沿边(c,e)转移，并将当前走过的路径更新为a→b→c→e，直到达到算法结束条件时蚂蚁停止行走。

该目标函数也可以作为蚂蚁行走轨迹质量评优标准，并权衡了路径边权值和和边平均权值两者之间的关系，利用α和β来调节两者的比重，并采用乘积的形式来放大结果之间的差异。目标函数取值越大，表示路径上边的信息流通权重越大，则该轨迹越有可能组成骨干网络。

3.2.3 自适应的信息素动态更新策略

在传统蚁群算法中，路径上的信息素用于引导蚁群找到到达食物源的最短路径。在蚁群每次迭代完成之后，都需要对信息素进行更新，更新具体包括信息素积累和挥发2 个方面。本文算法借鉴GBAS 算法[11-12]中的信息素更新方式，即采用信息素浓度反馈填补机制，在每次迭代结束后，将图中所有路径上挥发的信息素作为蚂蚁走过的路径上的积累信息素的总量，这种回填机制保证了整个网络中信息素浓度总量的恒定，即为初始时刻图中每条路径上的信息素浓度总和。

在信息素浓度迭代更新的过程中，往往存在某些路径上的信息素持续积累或挥发，进而导致路径之间浓度差异逐渐增大的现象。一些路径上的信息素一直挥发，使这条路径被选中的概率也越来越低；进而，频繁被选中的路径会积累更多的信息素。这一循环加剧了路径上信息素的差异，破坏了路径选择的随机性，使算法过早收敛。因此为了保证蚂蚁始终有着足够大的解空间，算法不会过早停滞，本文借鉴了MMAS 算法[22]的思想，为路径信息素浓度设置一个浓度变化区间，以保证路径上的信息素不会无限制的增加或减少。此外，利用回填机制为路径分配信息素积累量时，按照本代蚂蚁走过路径的目标函数值Fij(t)占路径集合目标函数之和SF(t)的比例进行计算，即。

然后根据蚁周模型将增加的信息素平铺在路径包含的所有的有向边上。值得注意的是，网络总体信息素量为定值，则每次挥发出的信息素总量也是定值，回填机制保证了网络信息素总量恒定。关于信息素浓度的具体计算式为

其中，ρ为信息素挥发系数，τij(t+1)为更新后边上的信息素浓度，τij(t)为第t代图中＜vi,vj＞边上的信息素浓度，(1−ρ(t))τij(t)为每条边上的信息素挥发后的残余量，Q为挥发的信息素总量。

在信息素的更新机制中，挥发因子的大小直接影响到蚁群算法的全局搜索能力和收敛速度，在处理大规模问题时，它的影响更突出。因此，本文在调节挥发因子的过程中引入动态自适应调节策略，即将挥发因子定义为一个和目标函数相关的值，根据每次迭代目标函数取值与历史取值的差异进行动态调整。具体地，当本次迭代的目标函数取值相比之前有所增大时，增大挥发因子，以增加蚂蚁走过路径的信息素积累量，从而加快算法的收敛速度；反之，则减小挥发因子，进而扩大蚁群的搜索空间。同时，为避免挥发因子过小，影响算法的收敛速度，对其设置一个阈值下界。动态改变的挥发因子ρ的计算式为

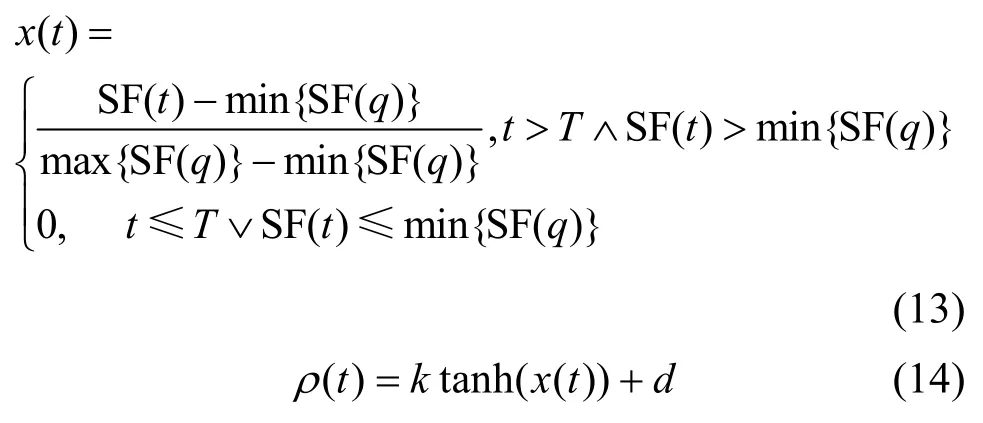
其中，q∈[t−T,t)，T为考察代数。对于时刻t，若t＞T，则考察[t−T,t)代的max{SF(i)}和min{SF(i)}，利用计算出每次迭代得到的目标函数值在历史迭代中的相对大小。

在迭代结束后，利用式(13)和式(14)计算出ρ(t)的值，再通过式(11)和式(12)对信息素τ进行更新。

在本问题中，每只蚂蚁所构造的解可能只是问题解的一部分，即每只蚂蚁的最优路径是骨干网络H的路径分支。定义2 中M和K的取值由实验确定。

本文采用的自适应动态调节机制利用信息素回填机制保证了蚁群有足够大搜索空间，利用挥发因子根据目标函数的变化进行动态调整，保证了算法可以得到一个满意解。

3.3 FNT-Ant 蚁群算法描述

输入信息交互网络G=（V,E,W）；参数α、β、ρ、m；挥发因子阈值X；迭代计数器NC；最大迭代次数NC_MAX

输出骨干网络H=(V′,E′,W′)

步骤1初始化α、β、ρ、m、NC_max ；根据式(6)初始化G，NC=0。

步骤2根据式(9)按照轮盘赌算法选择m个网络节点作为蚂蚁的初始位置。

步骤3针对任意蚂蚁k，若allowedk≠ϕ，则k根据式(1)选择下一节点，更新tabuk、allowedk，根据式(10)计算当前fl+1；若为空，则算法终止。

步骤4如果fl+1＞fl，则继续步骤5，否则回到步骤3 重新进行选择。

步骤5将所有蚂蚁走过路径的目标函数进行加和，按照式(13)和式(14)更新ρ值，进而按照式(11)和式(12)更新全局信息素。

步骤6NC+1，若NC＞NC_max，则转步骤7，否则转步骤2。

步骤7输出H={ρab|τ(ρab)＞X}。

4 实验与分析

根据前面的算法介绍，本文分别设计并实现了FNT-Ant 算法、贪心算法，然后对FNT-Ant 算法改进前后进行了对比实验，下面对实验结果进行比较分析。

4.1 实验设置

本文的实验环境为Windows 10，MATLAB R2017b。

4.2 实验数据

本文使用真实的金融日志，每条日志信息包含账号、对手账号、时间、方式、金额等属性信息。首先根据已获涉及金字塔影响的可疑名单调集其日志记录，随后又根据其对手进行两轮调集，形成包含35 842 个实体自其开卡之日起的所有日志组成的数据集，时间跨度为2014 年1 月到2018 年4月。本实验将数据集以年为单位进行划分并选取了2015 年的数据进行实验，利用该数据构建的交互网络中共包含35 842 个节点、101 699 条边。可见本文的交互网络存在骨干网络，即可疑涉及金字塔营销人员的交互关系网络。由于金字塔式经营模式中成员缴纳会费和收益的关系呈现金字塔型，因此担任不同角色的实体具有不同的信息流通特点。例如申购实体具有入对手多、出对手少且信息流通总量、频率皆较高的特点；Boss 实体具有出入对手数量少、流通频次低但流通量大的特点。可见，上述金融交互网络中不同角色的实体呈现不同交互特点（细节请参考文献[33]）。因此，在缺乏特定组织运作背景知识的前提下，难以量化实体的交互差异。但是，网络中信息的流向与分布，反映了核心骨干的收益情况。对该包含金字塔式经营的交互网络中骨干网络，可通过本文提出的FNT-Ant 算法进行提取。

4.3 对比实验结果分析

为了验证本文提出的FNT-Ant 算法的有效性和可行性，将FNT-Ant 算法和改进前的蚁群算法在目标函数值和收敛速度上进行比较，并将FNT-Ant 算法和贪心算法在骨干网络中的重点（可疑）节点覆盖率、准确率和节点角色分布进行了对比分析。具体介绍如下。

4.3.1 对比实验

为对比不同挥发因子和信息素更新策略和对算法结果的影响，设计了 FNT-Ant(S)算法、FNT-Ant(SP)算法和FNT-Ant 算法进行比较。其中FNT-Ant 算法的挥发因子根据目标函数动态调整，而FNT-Ant(S)算法和FNT-Ant(SP)算法均采用固定值；FNT-Ant 算法和FNT-Ant(SP)算法的信息素更新采用回填机制，而FNT-Ant(S)算法采用非回填机制。为了比较起点随机选择和起点结合网络中心性进行概率选择对算法结果的影响，对比分析了FNT-Ant(R)算法和FNT-Ant 算法。此外，本文还设计了贪心算法和FNT-Ant 算法进行对比，其区别在于贪心算法在进行路径选择时完全依据贪心策略，而FNT-Ant 算法则采用轮盘赌算法进行概率选择。具体的对比实验设置如表3 所示。

4.3.2 评价标准

本文将算法的收敛速度和最终得到的目标函数值作为评价算法性能优劣的标准，利用数据中已标记的重点节点及其角色信息，将轨迹中重点节点的覆盖率和准确率以及找到的节点角色分布作为算法有效性的判断标准。

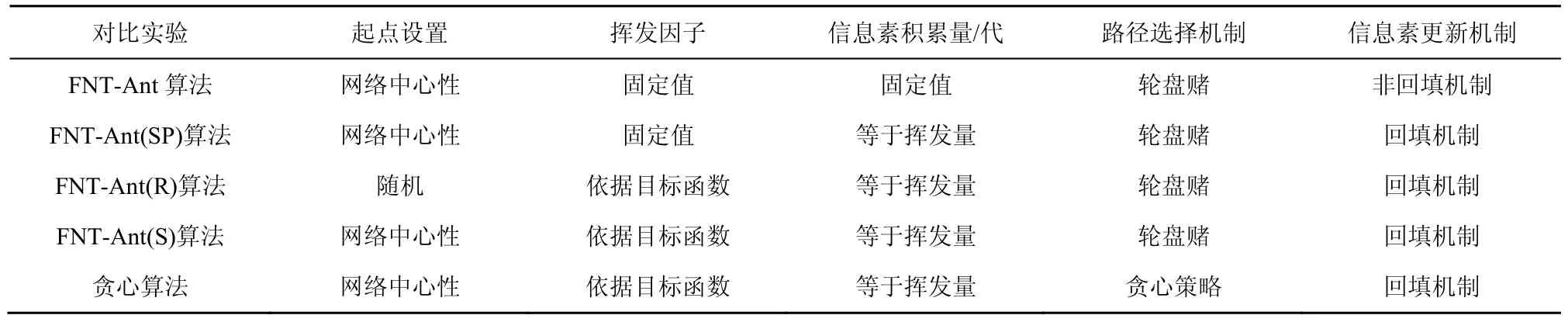
表3 对比实验设置

4.3.3 参数分析

本文构建的金融网络原始节点中心性分布数据如表4 所示。

表4 原始节点中心性分布数据

由于网络中节点的介数中心性数值过低，为使介数中心性重要度得以体现，需对其值进行放大处理，并利用tanh 函数进行规范化处理，如式(15)所示，即=tanh(k3BCi)，其中k3为介数中心性放大系数，其对金融网络中Level1 级别的节点（金字塔顶层节点，为Boss 角色）作为蚂蚁初始节点的概率变化曲线如图4 所示。

图4 Level1 级别的节点作为初始点的概率与k3 的关系

图4 中，横坐标为介数中心性的放大系数，纵坐标为Level1 级别的节点作为初始节点的概率，曲线上的圆圈表示最优值。由图4 可知，概率曲线随着介数中心性的增大，先迅速升高后开始趋于平稳并缓慢下降，当k3=62 时，Level1 级别的节点作为蚂蚁初始节点的概率最高。

当k3=62 时，k1和k2的取值对Level1 节点作为起始节点概率和所有异常节点（涉及金字塔经营的所有账户，记为全Level 节点）作为起始点概率的影响如图5 所示。

图5 Level1 和全Level 节点作为初始点的概率与k1 的关系

图5 中，横坐标为节点的度中心性系数k1，介数中心性系数k2=1−k1，纵坐标为网络中节点作为初始节点的概率，其中k1=0.4、k2=0.6为Level1节点作为起始点概率和全Level 节点作为起始点概率随k1变化曲线的拐点。此参数取值使起始概率在介数中心性作用下，重点异常节点作为起始点概率较大；在度中心性作用下，起始点有着足够大的扩展范围，蚁群可以进行大范围搜索。

实验的具体参数设置如下。信息素启发因子α=1，期望启发因子β=1，式(6)中的信息量、频次所占的权重分别为所占的权重a=0.5、b=0.5，对应系数分别为h1=1 ×10−5、h2=1 ×10−1。度中心性、介数中心性、介数中心性放大系数分别为k1=0.4、k2=0.6、k3=62。考察代数T=30，式(14)中的挥发因子更新系数k=0.05，挥发因子最小值d=0.005。

4.3.4 算法性能测试

算法的目标函数值代表了蚁群在骨干网络上积累的信息素总量。通过比较目标函数值的大小及算法的收敛速度对不同算法的性能进行分析。本节分别分析FNT-Ant 算法采用不同信息素更新策略和初始位置选择机制对算法性能的影响。信息素更新策略改进前后目标函数值的变化对比如图6 所示。

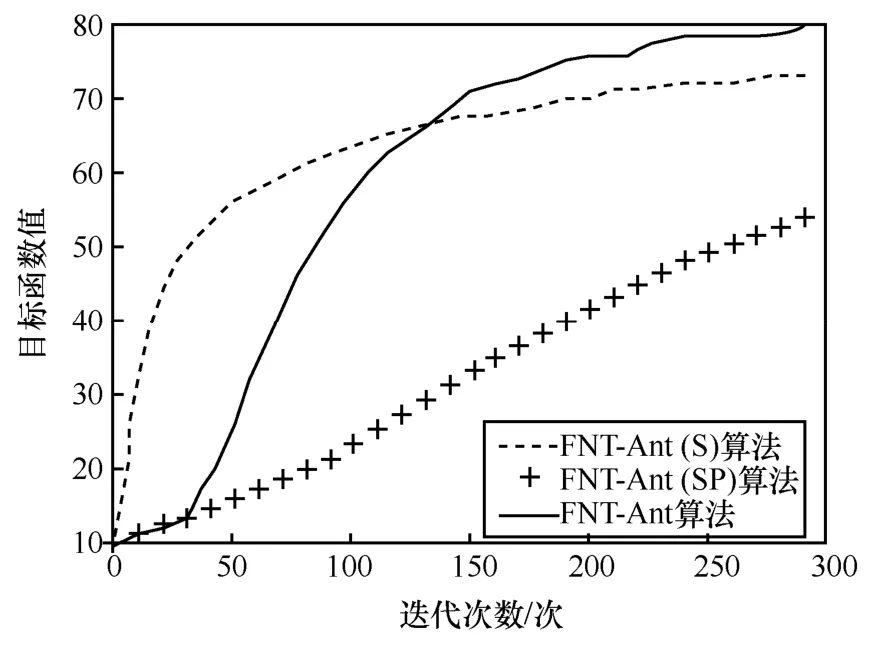
图6 算法目标函数值变化对比

图6 中横坐标为算法迭代次数，纵坐标为每代对应的目标函数值。从图6 中可以看到，FNT-Ant算法的收敛速度位于 FNT-Ant(S)算法和 FNTAnt(SP)算法之间，且在曲线走势趋于平缓时，FNT-Ant 算法得到的目标函数值高于其他2 种算法，这说明信息素的动态更新策略在一定程度上加快了算法的收敛速度，避免了算法早熟、停滞，且提高了解的性能，使最终得到的目标函数值更大。

当蚂蚁初始点设置采用不同策略时，算法目标函数值变化情况对比如图7 所示。

图7 算法目标函数值变化情况对比

图7 中横坐标为算法迭代次数，纵坐标为每代对应的目标函数值。从图7 中可以看到，采用起点结合网络中心性进行选择的FNT-Ant 算法的收敛速度及目标函数值均高于采用起点随机策略的FNT-Ant(R)算法。可见，起点选择策略改进后的FNT-Ant 算法具有更快的收敛速度，并且所得解的性能更优，避免了蚁群算法在未找到较好解时便早熟停滞。

4.3.5 算法有效性测试

本节通过对比不同算法对重点异常节点的覆盖率和准确率及角色分布来对算法的有效性进行说明。由于本文数据来源为涉及金字塔式经营实体的金融日志数据，因此该金融网络中隐藏着大量设计金字塔式经营的流通轨迹。为解决这一实际问题，FNT-Ant 算法的优化目标为尽可能让蚂蚁模拟有向流通路径，当算法收敛时，骨干网络中可疑节点的覆盖率和准确率越高，算法的性能也就越好。因此本文将标注数据中确定的重点异常参与者及其角色信息作为算法评价依据，对比分析了FNT-Ant 算法和贪心算法得到的骨干网络的覆盖率和准确率，实验结果如图8 所示。

图8 骨干网络可疑节点覆盖

图8 中横坐标为骨干网络包含的节点数量，纵坐标为异常节点的覆盖率和准确率，覆盖率即骨干网络中包含的异常节点占网络中所有异常节点的比重，准确率即骨干网络中包含的异常节点占其覆盖的所有节点的比重。这2 条曲线分别为FNT-Ant算法和贪心算法随着骨干网络的规模扩大，轨迹覆盖的异常节点个数的变化情况。

从图8 中可以看出，前期在相同轨迹节点数目情况下，贪心算法比FNT-Ant 算法找到的异常节点数目增速快，但当贪心算法找到的异常节点数目达到389 个时出现了转折，增速急剧放缓，很快覆盖率低于FNT-Ant 算法，并且之后一直低于。可见，贪心算法虽然在前期因优先选择权值大的路径所以快速找到了大量可疑节点，但由于其策略固定，没有发散能力，故在找到一部分权值大的路径后陷入局部最优，增速急剧放缓；而FNT-Ant 算法则能保持其增速直到找到所有可疑节点，FNT-Ant 算法在收敛速度、覆盖率和准确率这3 个方面均高于贪心算法。FNT-Ant 算法在最高准确率为28.52%时可疑节点的覆盖率达到了65.57%，而贪心算法在覆盖率同样为65.57%时，准确率为22.14%，由此可见，在找到同等数量可疑节点的情况下，FNT-Ant 算法比贪心算法的准确率更高，说明了FNT-Ant 算法在解决实际应用问题时的有效性。

金字塔式经营模式的成员角色关系架构也呈金字塔型，其组织发展模式具有固定性和裂变复制性。不同节点的信息流通量、交互频率等对组织的重要性不同，因此在组织中具有不同的角色。根据节点在组织中的重要性，将其按照重要程度递减的顺序依次划分为Level1、Level2 和Level3 共3 种角色。本文针对FNT-Ant 算法和贪心算法找到的可疑节点进行了进一步的角色分析，具体结果如图9 所示。

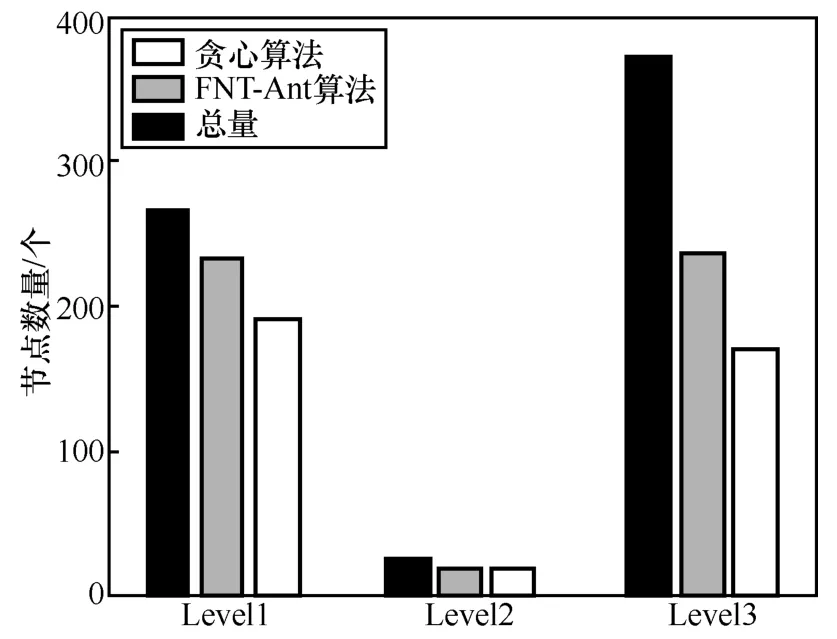
图9 可疑节点角色分布

图9 中横坐标为节点数量，纵坐标为角色层次。从图9 中可以看出，FNT-Ant 算法找到的所有层次中的角色数目均高于贪心算法，其中FNT-Ant 算法覆盖率最高的为位于Level1 层次的角色，其覆盖率达到了87%，而贪心算法的覆盖率为70%。由此可见，相比于传统的贪心算法，FNT-Ant 算法对具有重要角色的可疑节点覆盖率更高，这也说明了FNT-Ant 算法在骨干网络的发现上具有一定的应用价值。

5 结束语

本文将交互网络中的核心信息流通轨迹发现问题转化为网络上的路径寻优问题，提出了一种基于组合优化思想发现骨干网络的FNT-Ant 算法。FNT-Ant 算法以传统蚁群模型为依据，结合复杂网络中的节点中心性理论改进了交互网络中蚂蚁初始位置的选择策略，依据信息流通特点提出了一种交互网络中的路径转移机制，此外，为保证模型的收敛性能和寻优性能，提出了一种动态改变信息素挥发因子的自适应信息素更新机制。实验结果表明，FNT-Ant 算法在骨干网络发现问题上具有较好的求解性能和较快的收敛速度，并在金融网络的约减和异常分析上具有相当的应用价值。

本文的研究为蚁群算法在交互网络上应用的初探，算法为解决组合优化问题、资金追踪问题、主干路径发现问题提供了新思路。现阶段，算法对蚁群初始位置选择参考因素较少，在参数优化、算法的时间空间复杂度等方面还有进一步的研究空间。