地震行波对跨河谷高墩大跨桥梁地震反应的影响

郭昆霖 李小军 吴敬武 孙平宽 李邦武

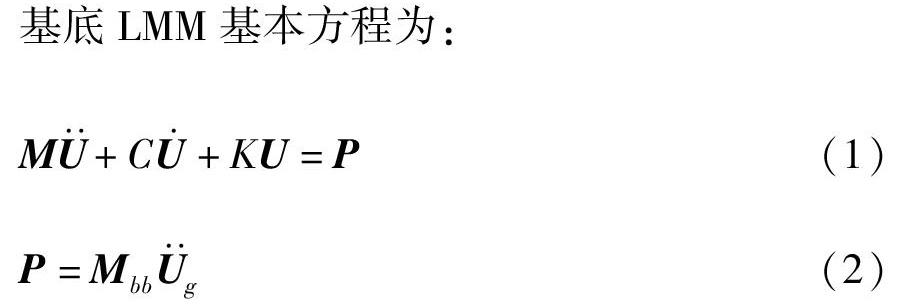
摘要：地震波行波效应会导致跨河谷高墩大跨桥梁各墩底基础处地震动到时产生差异，使桥梁结构地震反应变得更为复杂。通过构建高墩大跨桥梁结构模型，考虑墩高对称与非对称两种结构模型和不同频谱特性的地震动输入，采用大质量法开展了桥梁结构反应数值模拟，探讨了地震波斜入射的行波效应导致的桥梁各桥墩处输入地震动的时差对桥梁结构反应的影响。计算分析表明：①各桥墩处输入地震动的差异导致对称结构桥梁的反应出现极为不对称性，也加大了非對称结构桥梁的反应的复杂性;②桥梁结构反应内力改变且影响程度空间分布极为不均匀，高墩中间跨及高墩墩底受到影响较大;③随着地震波入射角度的加大，桥梁结构反应的改变程度总体呈增大趋势;④地震波入射角度对桥梁结构反应的影响特征与输入地震动的频谱特性密切相关。

关键词：河谷地形;大跨高墩桥梁;地震波入射角;地震动时差;地震反应

0 引言

我国位于环太平洋和亚欧地震带之间，地震灾害严重（胡聿贤，2006）。我国中西部多为山地、高原地区，在其公路、铁路交通工程建设中，多支撑的高墩长、大跨桥梁以其卓越的跨越能力得到快速发展，发挥着越来越重要的作用。近年来，大量的多支撑高墩大跨桥梁陆续建成，如 “亚洲第一高”——赫章特大桥、三水河特大桥和腊八斤沟特大桥等，其中桥墩高度超过 100 m的刚构桥已经超过 30 座，位居世界第一。

由于地形条件的限制，跨山区河谷高墩大跨桥梁一般具有以下特点：平、竖曲线的半径往往比较小，一般采用变墩高的曲线桥;其上部通常采用多联连续梁或连续刚构，下部多采用薄壁空心墩，墩高相差悬殊，结构复杂，长细比较大。高墩大跨桥梁在地震作用下的破坏有以下几种形式（叶爱君，管仲国，2001）：①桥台移位，倾斜;②墩台破坏及混凝土桥墩下部钢筋屈服、混凝土崩裂、压碎等;③支座破坏或脱落及支座本身构造上的破坏等;④相邻墩间相对位移过大导致主梁坠落。由此可见，地震造成山区跨河谷高墩桥梁结构破坏，很重要的原因是桥墩刚度和质量的不平衡。受地形条件限制，山区桥梁很容易形成结构刚度质量不平衡，相邻桥墩因高度不同导致刚度相差极大，使得水平地震力分布不均，导致刚度大的桥墩承受较大的水平地震力。因此，高墩大跨桥梁结构的地震影响已成为需要深入研究的一个问题（范立础，1997）。

地震波的传播特别是在斜入射情况下，会引起场地地表地震动空间上的差异，而局部场地地形和土层影响还将导致地震动强度和频谱上的差异，形成地震动的空间变化。在地震动的空间变化影响分析方面，最简单直接的是将其考虑为地震行波效应，即认为是地震波的传播导致地震动到时上的差异（Abrahamson et al，1991;Nelson et al，1977;Sand，1970），忽略幅值、频谱、持时等特性的改变。由于地震波的传播速度有限，地震波到达空间跨度较大的工程中的基础或支撑的时间必然存在差值（范立础，1997）。基于行波效应的地震动非一致输入方法是研究长大跨桥梁工程地震影响的主要方法，已取得了很多研究成果。目前，高墩大跨桥梁考虑行波效应主要关注地震动到达桥梁结构各基础处的时差对桥梁结构地震反应（Nazmy，Abdel-Ghaffar，1992;王明哗，2007;何庆祥，沈祖炎，2009;张沧海，2011;罗强，2014;王再荣等，2016;贾毅等，2019）、内力及位移（李忠献等，2005;张文，2009;陈清军等，2014;赵青等，2017）的影响。

以往对高墩大跨桥梁进行多点激励研究往往采用对称的桥梁模型，而在实际的工程中由于场地条件限制，桥梁结构往往难以做到对称。本文主要研究在桥梁主体结构相同的条件下改变墩柱高度以考虑非对称的桥梁结构模型，并输入不同特性的地震波，探讨行波效应对桥梁结构地震反应的影响特征。

1 结构多点激励的分析方法

工程结构多点激励分析的理论方法是相对运动法，但该方法基于叠加原理，原则上只适用于线弹性体系，因此限制了其在大型结构有限元程序中的应用。大质量法（Large Mass Method，简称LMM）由于计算路径简单，降低了大型复杂结构的计算难度，常被应用于实际工程问题。

LMM（Zhao et al，2006;Leger et al，1990）的基本思想是将结构基础假设为1个或多个附着于结构支撑点的具有大质量的集中单元M0（一般取值为104～106倍结构总质量），并释放基础运动方向的约束，在大质量点施加动力P（t）（其数值等于结构总质量与地震动加速度的乘积）模拟基础运动，实质是一种近似的方法。本文借鉴周国良等（2012）提出的LMM改进法，对输入进行了修正，提高了计算精度。

将式（3）第二行展开，当采用非质量相关阻尼，可推导出U · · g≈U · · b，输入基低的加速度U · · g=U · · b（a），若采用Rayleigh阻尼或质量相关阻尼，可推导出U · · b+αU·b=U · · g，即基底输入加速度应大于U · · b，才能使得式（3）成立，则输入应调整为U · · gnew=U · · b+αU·b（b）。

2 桥梁计算模型构建

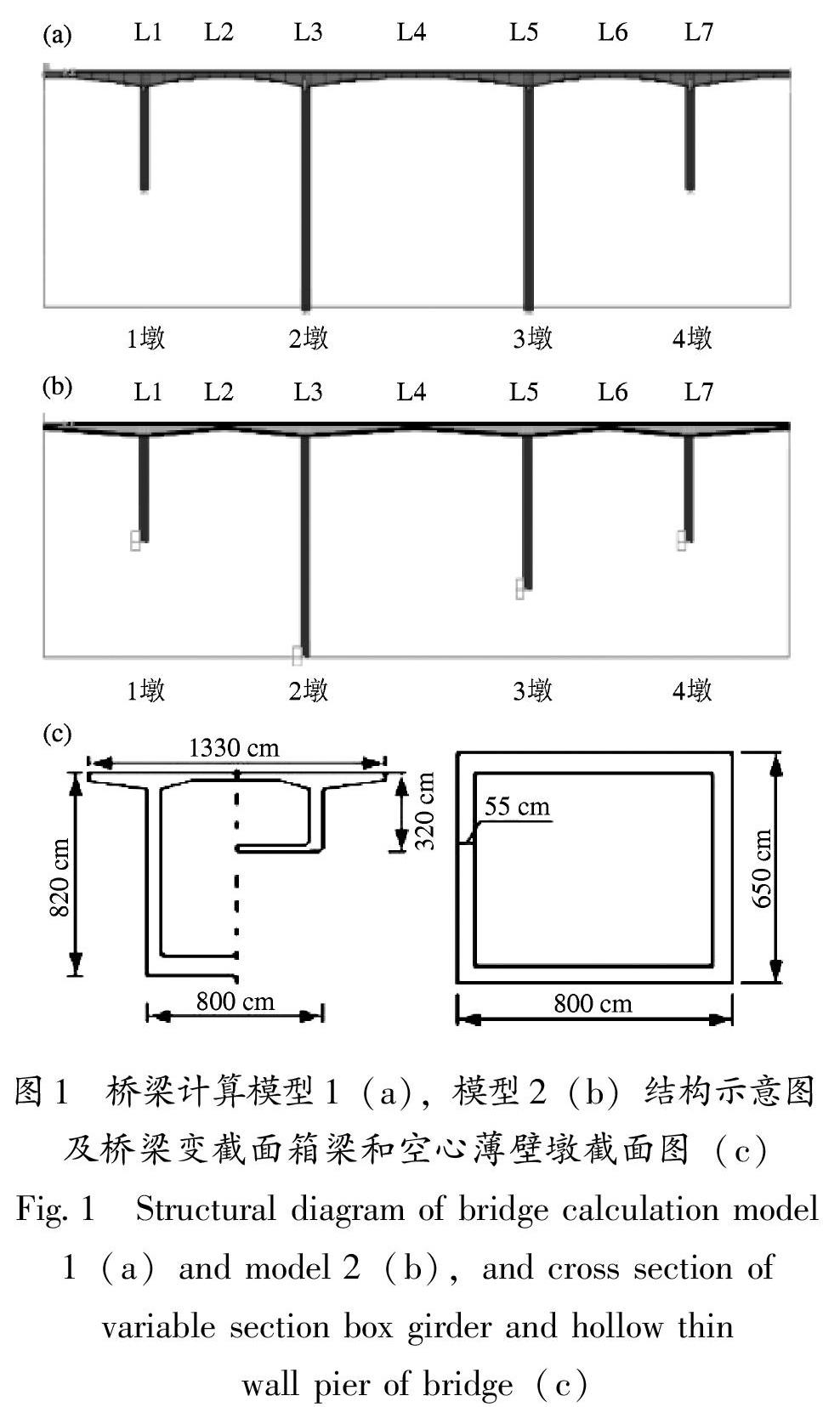
为了探讨地震行波效应对对称性与非对称性高低墩桥梁地震反应影响的差异性，根据高墩大跨桥梁抗震设计要求，本文分别构建了桥墩高度中心对称和非对称两个形式的桥梁结构计算模型。桥梁计算模型1为跨度组合为80+130+180+130+80 m的高墩大跨连续刚构桥（图1a），其主梁为变截面单室箱梁，桥墩为单室单箱薄壁空心墩（图1c），墩高分别为65，137，137，65 m，桥墩与主梁之间的连接形式为固结，梁、墩混凝土标号分别为C50和C40，其他构件混凝土标号为C30。主梁两端施加竖向位移约束、绕顺桥向转动约束;纵桥向采用线性弹簧单元支座，其他自由度释放（表1）。桥梁计算模型2如图1b所示，仅将桥梁计算模型1中3号桥墩高度改为95 m，其他参数不变。在有限元程序csibridge中采用空间梁单元模型，全桥划分600个单元，不考虑结构材料的非线性，结构视为粘弹性体。采用Rayleigh阻尼考虑结构阻尼，阻尼系数取值为α=0.314，β=0.007 63（周国良等，2012;周国良，2010;马保林，2001）。

3 数值模拟结果

在跨河谷桥梁地震反应计算中确定桥梁各桥墩基础处的输入地震动时，由于山区河谷场地地形效应会导致地震动强度和频谱上的差异，因此应综合考虑地震波传播的行波效应和地形效应的影响。但为了更清晰地分析地震波行波效应的影响，本文暂不考虑地形效应的影响，即各桥墩基础处输入地震动时程相同但存在到时差，其差值基于半无限弹性基岩空间中平面波传播理论解确定，基岩介质剪切波速设为1 000 m/s。

选用有限元软件csibridge，建立桥梁模型进行分析计算，计算中不考虑桥梁基础与地基的相互作用，即视地基为刚性。本文主要考虑2个不同入射角的地震波斜向入射情况进行数值模拟。桥梁结构地震反应分析工况设置见表2，其中工况①为地震波垂直入射情况，即视各桥墩基础一致地震动输入;工况②，③，④和⑤分别为地震波左侧30 °，60 °和右侧30 °，60 °入射角入射，各桥墩基础非一致地震动输入。由于模型左右两侧桥墩高度对称，只计算了地震波左侧30°和60°入射工况。数值模拟计算中，为了展示不同特性的输入地震动对桥梁结构反应的影响，分别采用El Centro地震动记录的SN分量（以下简称EC记录，PGA=3.42 m/s2）和Wolong地震动记录的EW分量（以下简称WL记录，PGA=9.57 m/s2）作为输入地震动，2条地震动记录的加速度时程和加速度反应谱如图2所示。由图2可见，EC记录和WL记录加速度反应谱明显不同，EC记录的频谱较宽，且有相对更丰富的低频成分。

考虑到跨河谷场地高墩大跨桥梁结构地震破坏的部位特点，选取主梁主要节点L1，L2，L3，L4，L5，L6，L7的轴力、剪力、弯矩以及各桥墩墩底节点P1，P2，P3，P4的剪力、弯矩进行具体计算分析研究。

在EC记录不同入射角输入情况下，计算得到桥梁模型1反应最大值影响的相对量（相对于入射角0的情况的差异相对值百分比）（表3）和主梁反应主要节点轴力、剪力和弯矩及墩底剪力、弯矩的最大值对比（图3a）从表3和图3a可看出，地震波入射角度不同对桥梁结构不同部位不同反应量有显著的影响，且反应量的变化并不一致，加大或减小并存;随着地震波入射角度增大，反应量差异总体上呈相对增大的趋势。桥梁主梁多数节点处的轴力增大（L5和L7最大值相对变化达到约20%），但桥梁主梁左侧跨和中跨L2，L3和L4的轴力有不同程度的减小，达到-22%;主梁中跨和左 侧跨L1，L3和L4的剪力增加（在L4达到176%），而主梁其它节点的剪力一定程度减小，达到-20%;主梁节点处弯矩变化的趋势与剪力的基本相反，主梁中跨和左侧跨L1，L3和L4的弯矩有一定程度的减小（节点L3处达到-23%），主梁其它節点的弯矩轻微增加。输入地震动的时差使得桥梁左侧P1和P2的剪力增大（P2达到75%），而桥梁右侧P3和P4的剪力减小（P4达到-31.7%）;桥墩墩底的弯矩变化的趋势与剪力的基本一致，桥梁左侧P1和P2的弯矩增大（节点P2处达到75.5%），而其右侧P3和P4的弯矩减小（P4达到-27.5%）。

综上，在一致地震动输入下，左右对称的桥梁结构模型1具有对称性的反应，但在地震波斜入射时，桥梁结构反应变得极为不对称，使得桥梁结构一些部位的反应量增大一些部位的反应量减小，且影响十分显著。对于桥梁主梁反应，影响最大的是中间跨主梁（节点L4处），剪力最大值提高了176%;对于桥梁桥墩反应，影响最大的是中间的高墩，墩底剪力最大值提高了75%，墩底弯矩最大值提高了75.5%。

在EC记录不同输入角输入情况下，计算得到桥梁模型2反应最大值影响的相对量（相对于入射角0的情况的差异相对值百分比）（表3）和主梁反应主要节点轴力、剪力和弯矩及墩底剪力、弯矩的最大值对比（图3b）。从表3和图3b可看出，地震波入射角度不同，对非对称桥梁结构反应的影响更为复杂;随着地震波入射角度增大（即各桥墩输入地震动时差的增大），反应量差异总体上具有相对增大的趋势，但地震波从左右两侧输入的影响程度有明显的不同。输入地震动的时差使桥梁地震波入射一侧两跨主梁节点处的轴力增加，最大值相对变化达20%，其它三跨主梁节点处的轴力减小，达-38%。当地震波从左侧入射时，桥梁主梁中跨L4的剪力出现了大幅度的增加，达145%，L3节点全部增加，而其他节点的剪力均有一定程度的减小，达到-20%;当地震波从右侧入射时，桥梁主梁节点的剪力均有一定程度的增加，L4达到179%。输入地震动的时差对桥梁主梁节点处的弯矩的影响相对较小，大多数节点的反应量有所减小，但最高墩顶位置L3和地震波输入一侧跨中L2或L6的反应量有一定程度的增加，达到13%。输入地震动的时差对桥墩反应的影响较大，地震波入射一侧的桥墩墩底的剪力增大，中间桥墩节点处达到80%，而另一侧桥墩墩底的剪力减小，两边桥墩节点达到-31.6%。输入地震动的时差对墩底的弯矩影响趋势与剪力的基本一致，地震波入射一侧的桥墩墩底的弯矩增大，中间桥墩达到82.6%;地震波左侧入射时的桥墩P2的弯矩略有增大、P4的略有减小，而另一侧桥墩墩底的弯矩减小，达到-37.5%;地震波右侧入射时桥墩P2的弯矩略有减小，P4的略有增大。

综上，在一致地震动输入下，不对称的桥梁结构模型2已具有明显的不对称性反应，当地震波斜入射时，桥梁结构反应变得更为不对称，桥梁结构一些部位的反应量增大，一些部位的反应量减小，且影响十分显著;对于桥梁主梁反应，影响最大的仍然是中间跨主梁（L4），剪力最大值提高了179%;对于桥梁桥墩反应，影响最大的是最高桥墩，墩底剪力最大值提高了80%，墩底弯矩最大值提高了82.6%，另一个高墩受到的影响与最高墩的很接近。

在WL记录输入情况下，计算得到了桥梁模型1和模型2的结构反应结果（图3c，d）。从图中可以看出，地震波的入射角对桥梁结构反应的影响与EC记录下的总体特征相近似，差别仅为在WL记录输入情况下，一致输入地震动的桥主梁轴力远大于地震波斜入射的轴力，这一现象产生的原因可能是结构自振频率与WL记录输入地震动的卓越频率成分接近有关，而地震动行波效应却改变了这一现象。该研究结果说明输入地震动的频谱特性对桥梁结构反应的影响显著，必须受到重视。

在不同角度地震波入射下，桥梁对称结构模型1和非对称结构模型2的地震反应规律有所不同。为进一步展示其影响特征，对2种模型的主梁反应的轴力、剪力和弯矩及墩底剪力、弯矩的最大值进行比较分析如图4所示，由图可见，地震波入射角度对对称结构还是非对称结构的高墩大跨桥梁地震反应的影响均很大，地震波入射角越大（即地震行波效应导致输入地震动的时差越大），其影响越明显;相对而言，对非对称结构桥梁的影响大于对称结构桥梁的;对主梁反应的影响中，高墩跨主梁的影响程度最大，且显著增大主梁跨中的剪力;对桥墩反应的影响中高墩的影响程度较大，且显著增大对称桥梁高墩的剪力和弯矩。这表明地震行波效应对高墩跨主梁及高墩反应不利，且十分敏感。另外，不同频谱特性的地震动输入时地震行波效应对高墩、低墩的影响程度不同，这说明地震行波效应的影响还与地震波频谱特性有一定关系。

4 结论

本文以高低墩大跨桥梁对称结构模型和非对称结构模型为对象开展数值模拟，探讨了地震波斜入射行波效应导致的桥梁各墩基输入地震动的时差对桥梁结构反应的影响，得到以下结论：

（1）地震行波效应对高低墩大跨桥梁地震反应有显著影响，相对而言，对非对称结构桥梁的影响程度要大于对称结构桥梁的。

（2）地震行波效应使得原本对称的结构桥梁反应也变为极为不对称，并显著加大了桥梁结构的一些部位的反应量;对于桥梁主梁反应，影响最大的是高墩中间跨主梁反应的剪力，剪力最大值提高可达175%以上。

（3）地震行波效应导致桥梁结构反应的内力改变显著，但影响程度空间分布极不均匀，且与地震波入射方向有密切关系;随着输入地震动时差的增大，桥梁结构反应的改变程度总体上具有相对增大的趋势。

（4）高低墩大跨桥梁结构抗震设计时应充分考虑非一致地震动输入的影响，应对地震波入射方向及其不确定性的影响给予足够重视。

本文研究结果主要针对所采用的桥梁结构模型和输入地震动特性得到，其对于其他结构形式的桥梁情况是否也适用，还有待于进一步研究。同时，研究复杂地形条件对桥梁结构地震反应的影响时，不应仅局限于地震行波效应导致的桥墩基础处地震动到时差异的影響，还需要考虑地形条件对桥墩基础处输入地震动的强度和频率变化的影响，今后将作进一步研究。

参考文献：

陈清军，张婷，陈志海，等.2014.长周期随机地震作用下超大跨斜拉桥的行波效应分析[J].湖南大学学报：自然科学版，41（4）：1-9.

范立础.1997.桥梁抗震[M].北京：人民交通出版社.

何庆祥，沈祖炎.2009.结构地震行波效应分析综述[J].地震工程与工程震动，29（1）：50-57.

胡聿贤.2006.地震工程学[M].北京：地震出版社.

贾毅，王永宝，李福海，等.2019.高墩大跨曲线连续刚构桥地震响应研究[J].沈阳建筑大学学报（自然科学版），35（1）：39-48.

李忠献，黄健，丁阳，等.2005.不同地震激励下大跨度斜拉桥的地震反应分析[J].中国公路学报，18（3）：48-53.

罗强.2014.基于ANSYS的连续钢构桥地震反应影响分析[J].山西交通科技，（1）：66-68.

马保林.2001.高墩大跨连续刚构桥[M].北京：人民交通出版社.

王明晔.2007.非一致输入下多跨连续梁桥地震反应分析[D].上海：同济大学

王再荣，孙利民，程纬.2016.超大跨斜拉桥地震行波效应分析[J].同济大学学报（自然科学版），44（10）：1471-1473.

叶爱君，管仲国.2001.桥梁抗震[M].北京：人民交通出版社.

张沧海.2011.大跨度桥梁多向多点激励下地震反应分析[D].哈尔滨：中国地震局工程力学研究所.

张文.2009.高墩大跨曲线连续刚构桥地震响应分析[D].成都：西南交通大学.

赵青，程旭，张宇.2017.行波效应对斜拉桥索力的影响分析[J].世界地震工程，33（1）：1471-1481.

周国良，鲍叶欣，李小军，等.2009b.结构动力分析中多点激励问题的研究综述[J].世界地震工程，25（4）：25-31.

周国良，李小军，李铁萍，等.2012.SV波入射下峡谷地形对多支撑大跨桥梁地震反应影响分析[J].岩土力学，33（5）：1185-1190.

周国良，李小军，刘必灯，等.2011.大质量法在多点激励分析中的应用＼误差分析及改进[J].工程力学.28（1）：45-48.

周国良，李小军，喻畑，等.2009a.结构地震作用的基底激励模型及其适用性[J].建筑结构学报，31（增刊2）：82-88.

周国良.2010.河谷地形对多支撑大跨桥梁地震反应影响[D].哈尔滨：中国地震局工程力学研究所.