集成学习在直线振动筛的应用及参数优化

李威宏，童昕，2，李占福，王耀坤

(1. 华侨大学 机电及自动化学院, 福建 厦门361021；2. 福建工程学院 福建省数字化装备重点实验室, 福建 福州 350108；3. 中建海峡建设发展有限公司, 福建 福州 350000)

筛分是日常生活中常见的粒子分离方法，广泛应用于煤矿开采、食品加工、垃圾处理等各个行业.筛分机械作为筛分作业使用的设备，对于产品的生产效率和生产质量都有着重要的提升作用[1-2].振动筛按其筛面振动的形式可分为直线振动筛、椭圆振动筛、圆振动筛，直线振动筛因其结构简单、工作可靠，备受企业的关注与应用.近年来,众多学者[3-4]展开了对直线振动筛筛分效率的研究，逐渐完善振动筛的筛分机理及参数优化.由于振动筛的筛分过程颗粒碰撞、受力与复杂多变运动，在实物试验中也难以进行测量，为此,采用EDEM软件在计算机上进行仿真模拟[5-6].Wang等[7]研究发现,用球形颗粒模拟自然界砂石颗粒，虽然具体的实验结果可能与非球面颗粒的结果有所差异，但所得出的变化规律却是相近的，说明用球形颗粒进行仿真模拟的可行性.Li等[8]应用机器学习的各种优化算法,对振动筛的筛分特征量和筛分参数展开深入的研究，发掘了更多潜在的规律，说明了机器学习算法在实验数据研究上的优势和便捷.但不管采用何种方法进行研究分析，都是基于一定量的实验数据，数据量的短缺很可能会造成所得到规律的不完整性及不确定性.为此，本文增加实验次数，从而获取更加全面可靠的数据，并使用集成学习对实验数据进行建模分析，力求更加全面准确地描述数据，最终输出高筛分效率下的筛机振动参数，为实际工程应用提供理论基础[9-12].

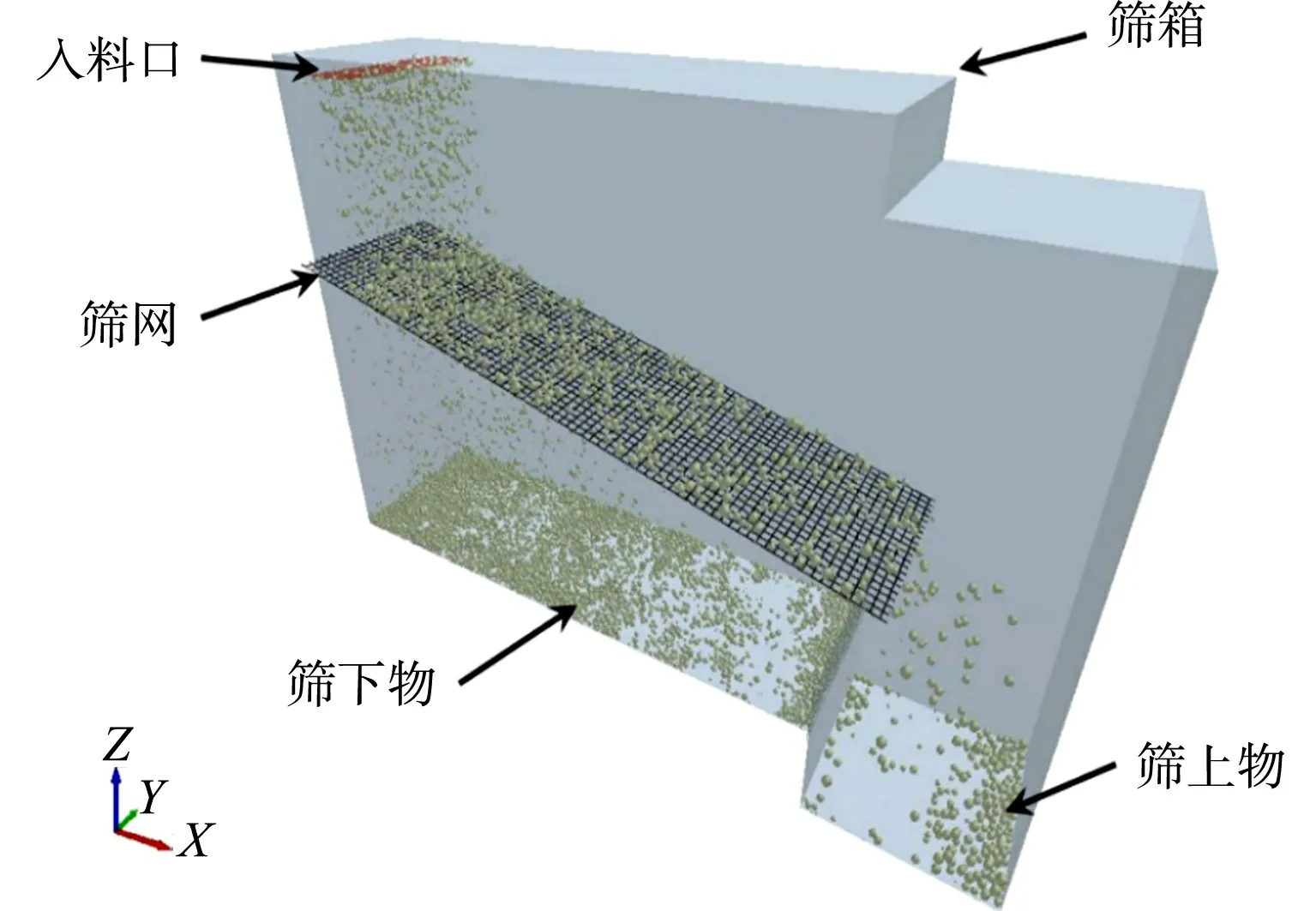
图1 EDEM软件中振动筛简化模型Fig.1 Simplified vibration screen model in EDEM software

1 模型的建立与仿真实验的设计

1.1 EDEM筛机模型的建立

采用EDEM软件仿真模拟筛分过程，分析筛分过程中的颗粒在筛面上的位置，确定其是否透筛.EDEM软件中振动筛简化模型，如图1所示.由图1可知：模型简化振动筛中其他多余的机械结构，主要保留了筛箱、筛网及产生颗粒的入料口3大部分.筛网模型作为仿真模型的核心部件，其形状大小主要根据工业上常用的钢丝编制的，孔型为正方形的筛网.

为了更好模拟自然界颗粒的分布状态，分别采用直径均值为0.5，1.0 mm双峰正态曲线生成的颗粒物料，颗粒的总数为20 000个，产生速率为13 333 颗·s-1[13].筛网的振动参数可以通过加载在筛网上的运动参数进行控制.EDEM模型材料的泊松比为0.30；剪切模量为23；密度为2 678 kg ·m-3.EDEM模型筛网、筛箱的泊松比为0.29；剪切模量为79 920；密度为7 861 kg ·m-3.EDEM模型材料颗粒与颗粒碰撞的恢复系数为0.1；静摩擦系数为0.545；滚动摩擦系数为0.01.EDEM模型颗粒与筛网、筛箱碰撞的恢复系数为0.2；静摩擦系数为0.500；滚动摩擦系数为0.01.

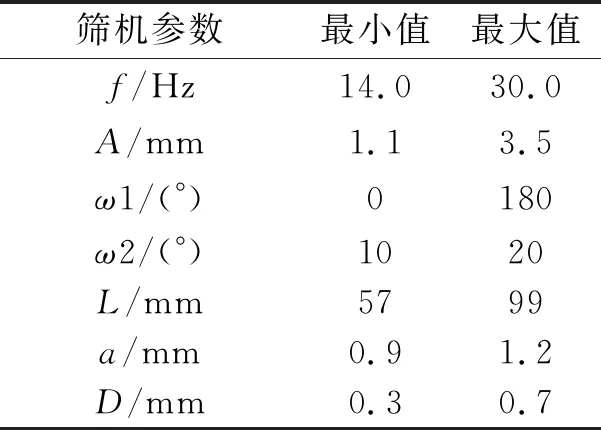
表1 筛机参数选取范围Tab.1 Selection range of screen machine parameters

1.2 仿真实验的设计

振动筛可控的参数很多，如颗粒的大小、形状、入料的速度、筛机的尺寸大小、筛网的形状等，因此，很难全部综合研究.而文中重点在于筛机的振动参数，其中，筛长将以其在水平面方向上的投影进行代替，方便实验的记录与进行.筛机参数选取范围,如表1所示.表1中：f为振动频率；A为振动幅度；ω1为振动方向角；ω2为筛面倾角；L为筛长；a为筛孔尺寸;D为筛丝直径.

根据以上7个因素取值范围，分别对每个因素取不同的水平值，再对这些实验组进行合理的筛选，在保证实验方案的均匀性和代表性的情况下减少实验次数，选出442组实验方案进行模拟仿真[14].

2 数据的处理与分析

2.1 筛分效率的定义

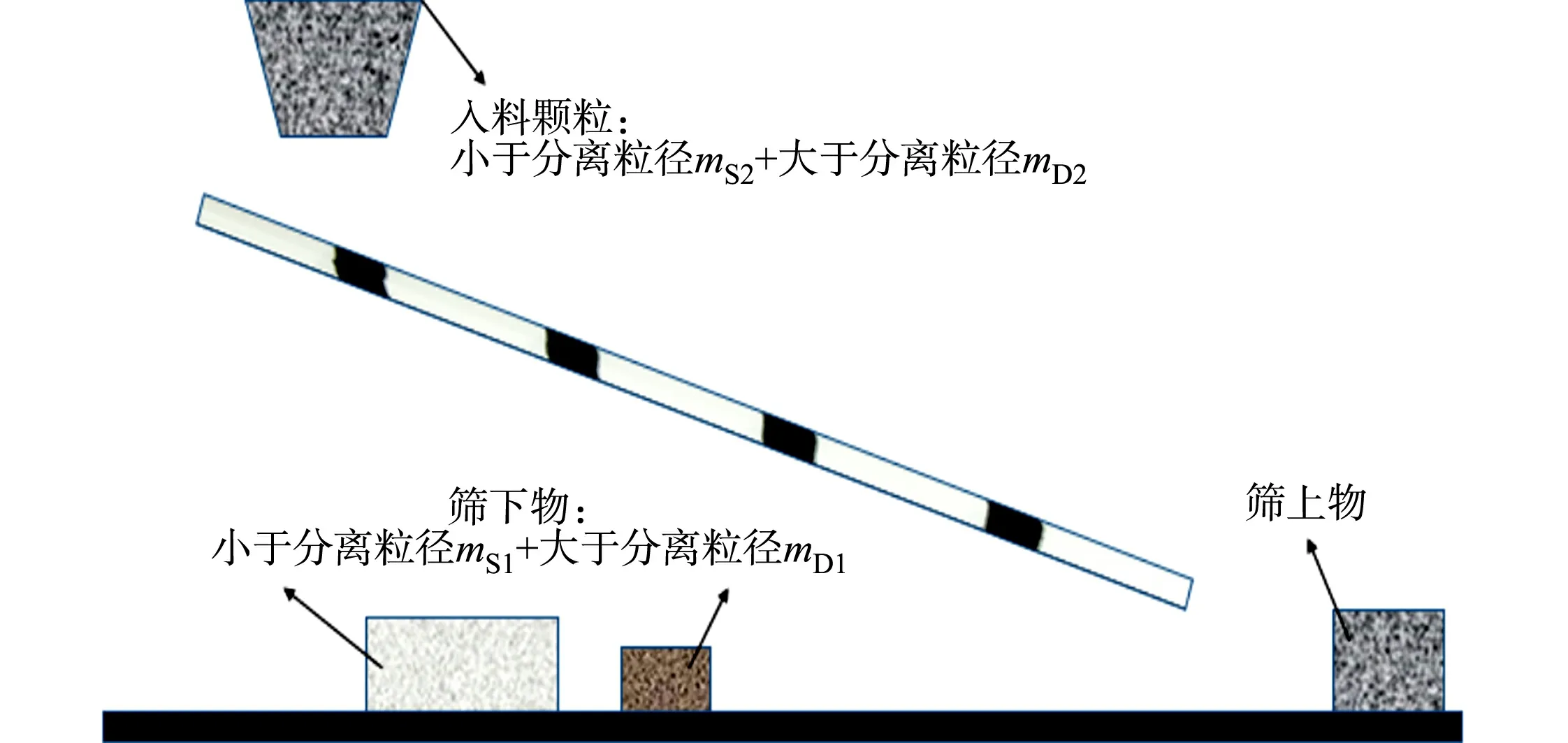
图2 入料与被筛物料关系Fig.2 Relationship of feeding and screened materials

根据与目标分离粒径，入料颗粒可分为小于分离粒径的,以及大于等于分离粒径的，这两部分的质量分别用mS2,mD2表示，文中所用的目标分离粒径均为0.9 mm.经筛分后，入料颗粒或者成为筛下物，或者成为筛上物.试验中出现筛孔尺寸大于分离粒径的情况，因此，筛下物中不仅有小于分离粒径的颗粒，还可能会存在着大于分离粒径的颗粒，其质量分别用mS1,mD1表示.入料与被筛物料关系，如图2所示.筛分效率为

(1)

2.2 数据模型的建立

2.2.1 集成学习 集成学习的主要思路是集合多个子模型，综合每个子模型的判断结果进行投票选择，最终做出判断.在每个子模型判断精度不需要都很高的情况下，最后的决策也能达到很高的精度，同时，还可以兼顾到每个不同子模型的优势[15].如在二分类问题中，在每个子模型的判断精度仅为p=60%的情况下，当集合了N=500时，其准确率为

(2)

由式(2)可知：集成学习在数据处理上的能力和准确性都是不错的.将实验得到的442组数据分为两组：训练集占80%；测试集占20%.训练集用于模型的训练，而测试集则用来测试所得模型的准确性和泛化性，以免模型发生过拟合或者欠拟合.

集成的子模型是决策树模型，经过多次的调参后，确定决策树中的最大深度为4层，并使用有放回取样(out of bag,OOB)模型[16]，样本为500个，每次取320个，模型在训练集的训练效果及测试集的训练效果，如图3，4所示.图3,4中：ηp为预测筛分效率；ηe为实验筛分效率.

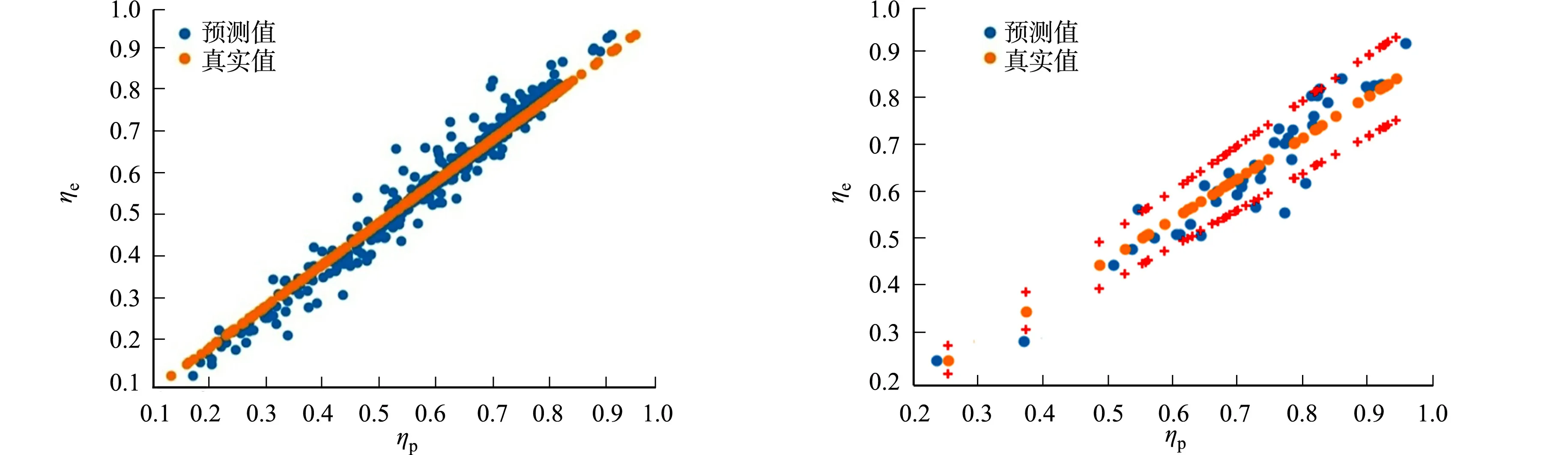
图3 模型在训练集的训练效果 图4 模型在测试集的训练效果Fig.3 Training effect of model in the training set Fig.4 Training effect of model in test set

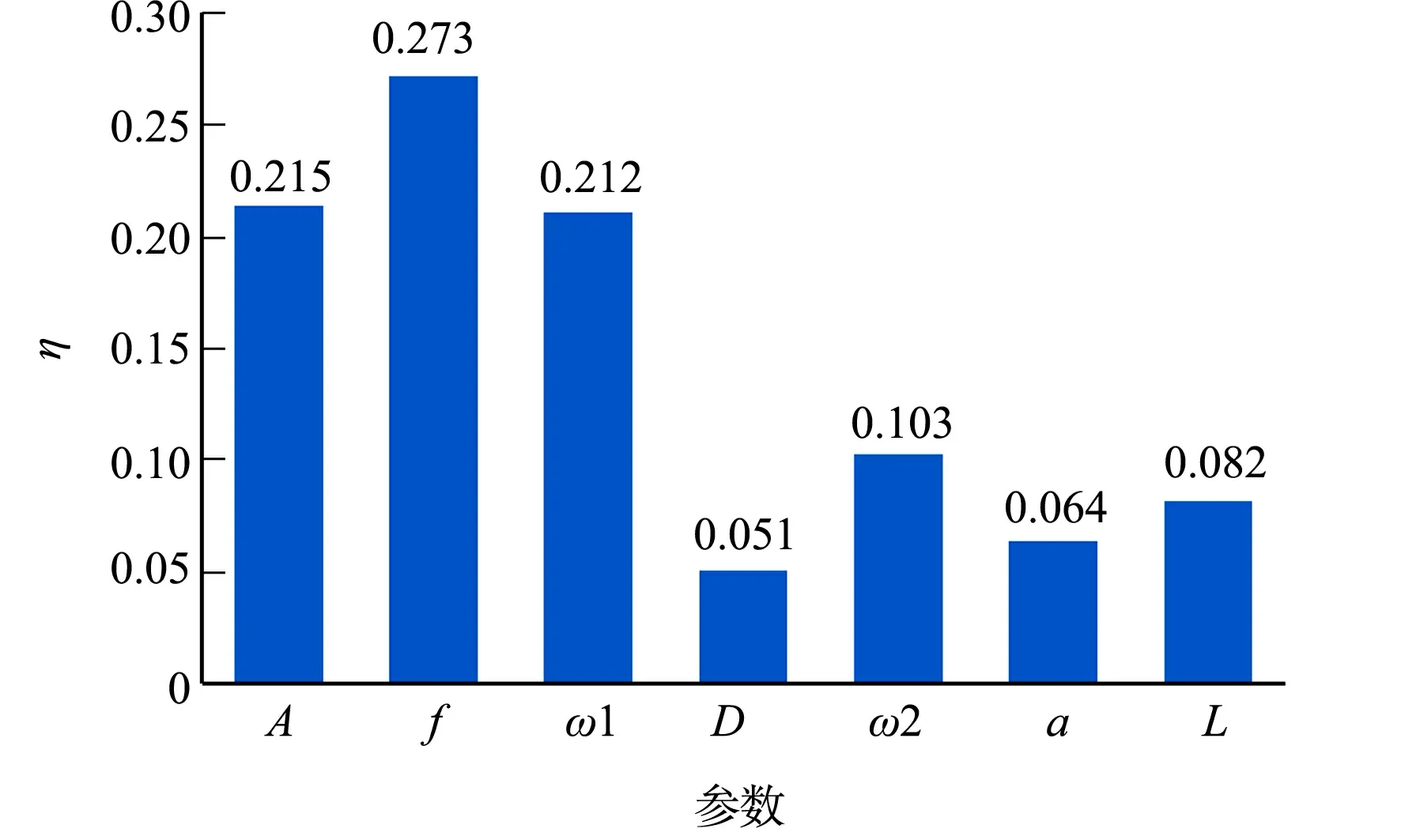
图5 筛机参数影响筛分效率的权重Fig.5 Weights of different vibration parameters on screening efficiency

由图3,4可知：模型不管在训练集还是测试集上都有较好的吻合度，尤其是测试集上的表现效果，更能体现模型的适用性及可靠性，其预测值偏差基本都在10%以内，少数几个偏差在10%以外.

2.2.2 影响权重的分析 筛机的筛分效率影响因素众多，在工程上的调整难免会出现一定的盲目性，导致调整的效果变化多样.采用集成学习的XGBoost(extreme gradient boosting),对训练好的模型进行筛机参数影响权重的分析[17]，筛机参数影响筛分效率的权重,如图5所示.图5中：η为筛分效率.

对筛分效率影响最大的是振频、振幅及振动方向角(图3，4).在振频和振幅的协同作用下，筛面上的颗粒在一定的空间范围内上下窜动.当筛网由波谷向波峰运动时，筛面上的颗粒不断被挤压堆积；当筛网从波峰向波谷运动时，筛面上的颗粒在重力的作用下开始散落.通过不断挤压和松散，小颗粒不断下沉和透筛，大颗粒不断上浮和流动.筛面位于波峰时，筛上颗粒平均质心位置与筛网位置的距离为d1，筛面位于波谷时，筛上颗粒平均质心位置与筛网位置的距离为d2.实验表明：d1与d2之差d约为1.3倍筛孔尺寸a时，筛分效果较优，即

d=d2-d1≈1.3a.

(3)

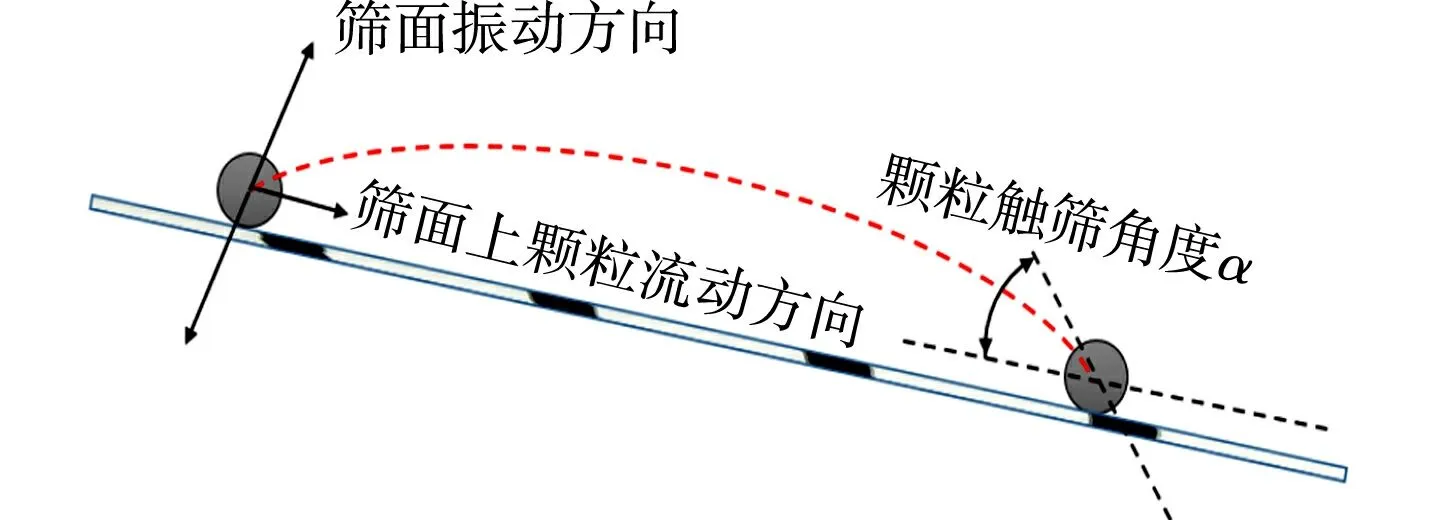
图6 筛上颗粒在筛分过程中的触筛角度Fig.6 Contact angle of particles on screen during screening

振动方向角主要作用是控制着筛上颗粒跳动的方向，从而直接影响着颗粒的触筛角度α，进而引起筛分效果的变动.触筛角度α过小时，筛上颗粒得不到充分的松散，不利于小颗粒的下沉透筛；而当α值过大时，筛上颗粒的流动能力受到限制，从而影响筛分的效率.实验数据的统计表明，当触筛角度α控制在12°～23°时，可以实现良好的筛分效果.筛上颗粒在筛分过程中的触筛角度,如图6所示.

3个振动参数为筛面上颗粒的跳动提供了主要的能量，使其在一定的空间范围内错开分布，便于小颗粒的下落透筛，以及大颗粒的流动转移，促进物料的持续筛分.而对于筛孔和筛丝直径，一旦确定整个筛网镂空面积和筛网总面积比例，他们两者的变化对筛分效率就起不到太大的作用，因此，影响权重较小.

2.3 粒子群算法参数寻优

最优化问题的目的是找到使目标函数达到最值条件.传统的优化方法有牛顿法、共轭梯度法、模式搜索法和单纯形法等，通过一次次的迭代寻找最优值[18].近年来，粒子群算法在数据处理上有了更多选择，其特点是简单便捷、收敛速度快、不易陷入局部最值、涉及的理论知识较少等.

粒子群算法是受鸟群觅食行为的启发而建立的一种智能优化算法，可运用在多种情况下的最优化问题.粒子群算法流程图,如图7所示.算法迭代的效果,如图8所示.图8中：fbest是函数最优值;n为迭代次数.

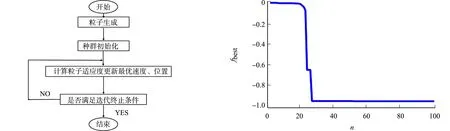
图7 粒子群算法流程图 图8 算法迭代的效果Fig.7 Flow chart of particle swarm algorithm Fig.8 Effect of algorithm iteration

首先，在7个维度上随机生成500个粒子，且在每个维度上设置其搜索的范围.初始化后每个粒子都包含两个信息量：位置信息P，速度信息V，将其两个信息量代入适应函数fx，i,求出其适应值，比较得到粒子i在7个维度中经历过的最好位置pbesti为

pbesti=(pi1,pi2,pi3,pi4,pi5,pi6,pi7).

(4)

所有种群粒子经历过的最好位置gbesti为

gbesti=(g1,g2,g3,g4,g5,g6,g7).

(5)

每个粒子i在不同维度μ移动搜索过程中的速度更新公式为

(6)

位置更新公式为

(7)

为了遵循优化算法的惯例，将是筛分效率最大值转化为最小值问题，目标函数为fi=-η.

完成基本参数的设置之后,将训练好的模型放入粒子群算法中进行迭代搜索.经过迭代后,最优参数组合及筛分效率如下：振幅为1.27 mm；振动方向角为17.0°；振频为14.1 Hz；筛长为98.9 mm；筛孔尺寸为0.90 mm；筛丝直径为0.67 mm；筛面倾角为-10.7°；筛分效率为0.946.

2.4 优化结果的验证

为了验证模型建立和优化算法的可靠性与准确性，随机选取优化筛分效率较高的10组筛机参数，将其再进行一次仿真实验，得到的结果与算法预测值对比分析，优化筛机参数的验证，如表2所示.

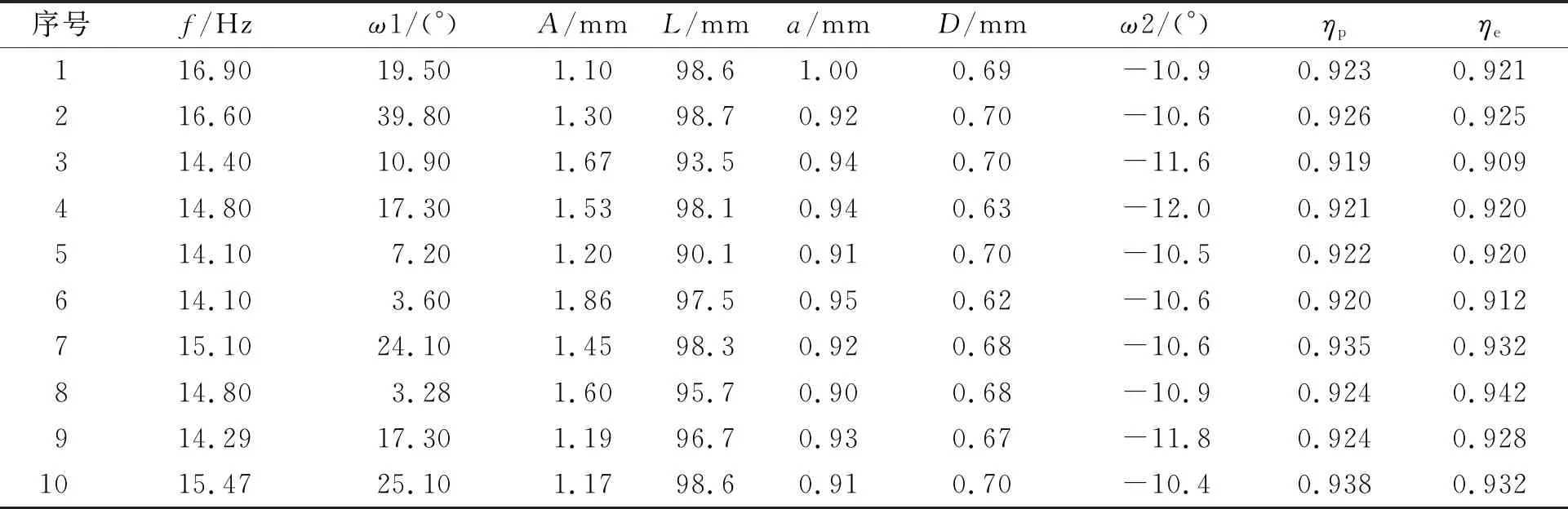
表2 优化筛机参数的验证Tab.2 Verification of optimized screen machine parameters

由表2可知：预测的优化参数在仿真实验中同样有着良好的表现，其最终的效率值和预测值差异性只在4%的范围内波动，说明了文中模型建立和优化算法的准确性和稳定性.

实验数据统计分析图，如图9所示.由图9可知：当d约为1.3倍的筛孔尺寸a时，其筛分效果好，且对应的触筛角度α在12°～23°浮动.

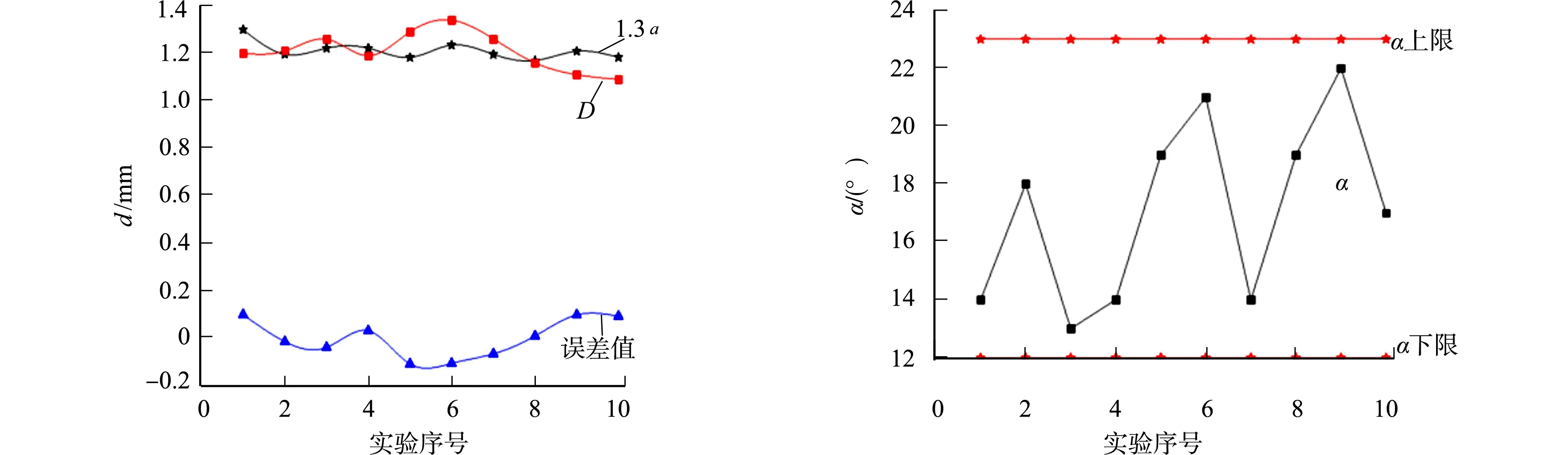
(a) 距离差值 (b) 触筛角度值图9 实验数据统计分析图Fig.9 Statistical analysis chart of experimental data

3 结束语

对直线振动筛的筛机参数展开优化求解，通过对实验的设计到数据的处理，最终得到高筛分效率值的各个筛机参数，为工程上的筛分优化提供理论基础和指导方案，有以下3个结论.

1) 对7个筛机参数选取合适的水平值，在确保实验全面性和代表性的前提下减少试验次数，最终设计442组试验，简化筛机模型，将其核心部分导入离散元EDEM软件进行筛分仿真实验.

2) 提取仿真实验的实验数据，运用集成学习的方法集成多个决策树子模型对数据进行分析建模，得出7个不同筛机参数对筛分效率的影响权重，并对前3个影响权重最大的参数进行探讨，当d约为1.3倍的筛孔尺寸a时，具有良好的筛分效果，且对应的触筛角度值α在12°～23°浮动.

3) 采用粒子群算法对建立好的数学模型进行参数寻优，求出高筛分效率对应的筛机参数值，此外，再随机挑选出10组优化过的筛机参数值，重新做一次仿真实验，验证模型建立和算法优化结果的准确性及所得结论的可靠性.