预压力对压电驱动履带移动系统的性能影响*

王 亮， 陈 迪， 王 鑫， 张 泉， 金家楣

(1. 南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

(2. 上海大学机电工程与自动化学院 上海，200072)

引 言

深空探测技术已成为衡量一个国家综合国力和高端技术创新能力的标杆，在提升国际影响力、保障国家国防安全等方面发挥着重要的推进作用[1]。我国在本世纪初制定了嫦娥探月工程计划，拟在2020年前后完成对月球开展的“绕”、“落”、“回”三步探测任务，为我国进一步开展载人登月以及在未来实施火星等外太空行星的探测进行技术储备[2]。美国制定了2024年前载人重返月球的计划[3]。

在探月工程实施方案里，月面巡视器(俗称“月球车”)扮演了重要的角色，是月面探测任务的重要载体和探测装置[4]。2013年，我国研制并成功发射的嫦娥三号探测器所携带的“玉兔”一号月球车在月面上行驶的辙印是我国首次在月球上留下的足迹。2018年底，嫦娥四号探测器开启了探月之旅并成功着落在月球背面，携带的“玉兔”二号月球车也成功落月，截至目前为止，“玉兔”二号月球车仍在月面上工作。虽然多功能集成化设计能够保证月球车同时执行多项探测任务，但是功能模块的不断增加及其相互之间的交叉融合以及复杂的月面环境，使得月球车的可靠度保障成为一项艰巨任务。随着传感、人工智能技术的快速进步，微小型群机器人系统成为了月面巡视器发展的新方向。

尽管轮式机构已成为月面巡视器的主流移动系统，但是越障能力差以及非道路机动性能受限等缺点，仍对轮式月面巡视器适应复杂月面环境提出了严峻的挑战[5]。履带式机构的设计是为了适应崎岖、凹凸不平的行星表面形貌，具有较强的越障能力和较高的稳定性，但结构复杂、机动性能差、控制系统冗余，距离实际应用还有很多工作要做[6]。2000年，欧洲空间局研制了一款微小型履带式火星探测车，可实现5 m/h的运行速度和0.1 m的越障高度[7]。2009年，日本宇航探测局研制了一款微小型多履带式月面巡视器，可实现高机动性能[8]。2012年，美国国家航空航天局开发出了一款可在行星表面进行勘探任务的微小型履带车[9]。上述微小型履带车的设计方案给微小型月面巡视器提供了新思路，但是系统结构复杂、笨重、磨损严重、效率低和功耗大等问题仍未被彻底解决。课题组在长期研究行波型旋转超声电机的基础上[10-13]，利用超声电机具有的环境适应性好、结构简单紧凑、直接驱动无需减速机构、断电自锁和快速响应等优点，提出了结构功能一体化的压电驱动履带移动系统的设计思路[14-18]，解决了传统履带系统存在的驱动轮系复杂、重量大、能耗高和磨损严重等问题，特别是消除了真空环境下运动副需要润滑的问题。

利用环形结构的面内弯曲振动，基于环梁结构复合形式，课题组提出了贴片式和夹心式两种行波型压电振子用于驱动履带构建移动系统[14-16]。4个圆环通过4根粘贴了压电陶瓷片的直梁构建了平行四边形框架式压电振子，其中4个圆环位于四边形的4个顶点。两相面内弯曲模态在4个圆环上耦合出同向旋转的行波，通过摩擦作用驱动张紧在4个圆环外表面的履带运动[14-15]。由于利用了压电陶瓷的d31振动特性，贴片式四环形压电振子存在机电耦合效率低和驱动效果差等问题，导致构建的履带移动系统输出性能较差，现阶段难以满足微小型月面巡视器的应用需求。在此基础上，课题组利用压电陶瓷的d33振动特性设计了夹心式双环形压电振子，利用两相面内弯曲振动在2个圆环上形成同向旋转行波，经摩擦作用驱动履带运动，从而构建履带式移动系统[16-18]。初步实验结果已表明，夹心式压电振子的驱动性能优于贴片式压电振子，但仍无法满足微小型月面巡视器对移动系统的应用需求。其主要原因在于夹心式压电振子驱动的履带移动系统没有考虑预压力对系统输出性能的影响关系，两者之间的预压力仅靠履带自身的张紧力，无法满足系统性能提升的要求[19]。

课题组在原有夹心式压电驱动履带移动系统的基础上设计了预压力调节机构，用于调整夹心式压电振子与履带之间的预压力，从而改进履带移动系统的机械输出性能。首先，通过有限元仿真分析讨论了设置有预压力调节机构的夹心式压电振子的动力学特性；其次，开展了预压力调节机构作用下不同预压力对夹心式压电驱动履带移动系统性能影响关系的实验研究，并与无预压力调节机构的夹心式压电驱动履带系统的性能进行了比较；最后，总结了预压力调节机构对夹心式压电驱动系统的性能影响关系。

1 预压力调节机构的设计

笔者提出了一种U型预压力调节机构，如图1所示，具有灵活调节夹心式压电振子与履带之间预压力的能力。2个半U型夹持机构通过螺栓固定在夹心式压电振子的连接块中央，构成一个完整的U型结构。此外，半U型夹持机构的侧面设置了U型凹槽。一根在两端设置了外螺纹的金属杆通过2个螺帽固定在2个半U型夹持机构的U型凹槽内，用于调节履带与夹心式压电振子的预压力。其中，在金属杆的中央固定了一个滚动轴承，以减小预压力调节机构对履带移动系统性能的影响。

图1 U型预压力调节机构示意图Fig.1 Schematic of the U-shaped preload adjustment mechanism

图2为安装了预压力调节机构的夹心式压电驱动履带移动系统示意图。为了降低预压力机构对夹心式压电振子的振动特性影响，2个半U型夹持机构安装在夹心式压电振子的连接块中央，此处位于兰杰文换能器的3阶纵振和10阶弯振的公共节点。

图2 安装预压力调节机构的夹心式压电驱动履带移动系统示意图Fig.2 Schematic of the sandwich piezoelectric actuated tracked mobile system with the preload adjustment mechanism

2 仿真分析

为了研究U型预压力机构安装在夹心式压电振子上对其振动特性的影响关系，笔者利用有限元软件ANSYS/Workbench对安装有U型预压力机构的压电振子进行了仿真分析。首先，建立了2个半U型夹持机构与夹心式压电振子复合后的有限元模型，如图3所示。整个复合结构的有限元模型共有39 096个单元和67 440个节点。压电振子与半U型夹持机构的材料选择如下：变截面梁和驱动圆环为磷青铜，连接块为65Mn，5个螺栓为45钢，半U型夹持机构为不锈钢，压电陶瓷片为PZT-8型号(无锡海鹰集团，部分材料参数为d33=250 pC/N，Kp=0.31，Qm=1 500，长为12 mm，宽为8 mm，厚度为2 mm，中间设有直径为4 mm的通孔)，具体材料参数见文献[17]，其中，半U型夹持机构的尺寸示意图如图4所示。在保证计算精度的条件下，对实际的夹心式压电振子做了必要的简化和假设。没有考虑预紧螺栓施加在压电陶瓷片上的预紧力，且假设所有零件之间的结合面都是连续的。

图3 2个半U型夹持机构与夹心式压电振子复合结构的有限元模型Fig.3 Finite element model of the composite structure of the two half-U-shaped clamping mechanisms and the sandwich piezoelectric actuator

图4 半U型夹持机构的尺寸示意图(单位：mm)Fig.4 Dimensional view of the half-U-shaped clamping mechanism (unit: mm)

对4组压电陶瓷片进行了零电压约束，通过模态分析计算得到了压电振子的2个工作模态(模态A和模态B)，如图5所示。在模态A中，兰杰文换能器呈现出3阶纵振，2个驱动圆环呈现出在4阶面内弯振，并且2个半U型夹持机构位于兰杰文换能器3阶纵振的节点位置。在模态B中，兰杰文换能器呈现10阶弯振，2个驱动圆环也呈现出4阶面内弯振(但与模态A中的4阶面内弯振在空间上存在π/2相位差)，同样2个半U型夹持机构位于兰杰文换能器10阶弯振的中间节点位置。模态A和模态B分别对应的共振频率为35.122 kHz和35.529 kHz。可以看出，在计算得到的2个模态中，2个半U型夹持机构均呈现出弱振动的形态。虽然2个半U型夹持机构的安装未改变压电振子原有工作模态的振型，但由于附加质量的增加以及整体结构的改变，导致2个工作模态的共振频率发生漂移，同时加大了2个工作模态的频率差。

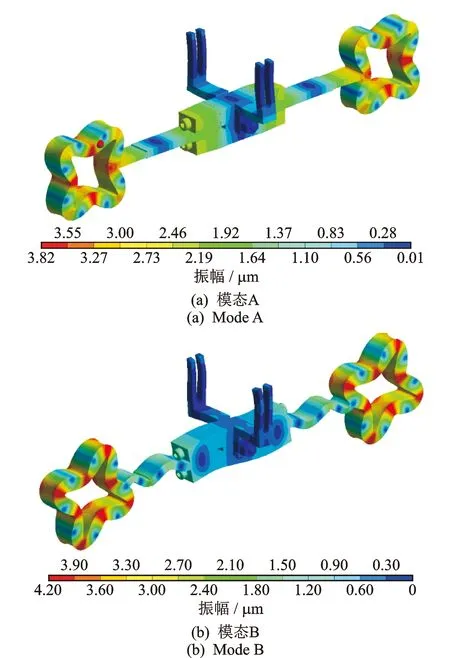
图5 模态分析计算得到的2个工作模态Fig.5 Two operating vibration modes calculated by the modal analysis

为了进一步研究半U型夹持机构的安装对夹心式压电振子的影响特性，笔者开展了谐响应仿真分析。选取了100 V的激励电压和35.35 kHz的激励频率，计算得到了夹心式压电振子在一个振动周期内的振型变化情况，如图6所示。将夹心式压电振子的一个振动周期分为4个阶段，可以看出，在这4个阶段里，一个完整的沿周向行进的行波在夹心式压电振子的驱动圆环上形成。此外，从夹心式压电振子的变形云图可以看出，2个半U型夹持机构在一个振动周期内始终处于微弱振动状态。因此，2个半U型夹持机构的安装并未改变夹心式压电振子的振动模态。

图6 夹心式压电振子在一个振动周期内的振型变化情况Fig.6 Vibration shapes of the sandwich piezoelectric actuator during one vibration period

3 实验研究

为了研究预压力对夹心式压电驱动履带移动系统的机械输出性能的影响关系，将 U型预压力调节机构安装在夹心式压电驱动履带移动系统上，如图7所示，并开展了相关的实验研究。

图7 设置了U型预压力调节机构的夹心式压电驱动履带移动系统的原理样机图Fig.7 Prototype of the sandwich piezoelectric actuated tracked mobile system assembled with the U-shaped preload adjustment mechanism

3.1 测振实验

首先，利用多普勒激光测振仪(Polytec， PSV-330F-B，德国)对安装了U型预压力调节机构的夹心式压电振子进行测振实验，确定其振动特性。测振实验结果如图8所示。以夹心式压电振子的一根变截面梁以及与之相连的一个驱动圆环为测试对象，通过扫频实验得到了如图8(a)所示的幅频曲线图。测试得到的两相工作模态的共振频率分别为35.14和35.44 kHz，频率差为300 Hz。对应工作模态的共振频率与有限元仿真结果接近，说明有限元仿真结果的正确性。基于扫频结果得到的两相工作模态的共振频率，对夹心式压电振子进行了定频实验，结果如图8(b)所示。可以看出，夹心式压电振子通过测振实验得到的两相工作模态A和B的振型与有限元仿真结果基本一致，进一步验证了有限元仿真分析的正确性。

图8 安装有U型预压力调节机构的夹心式压电振子测振实验结果Fig.8 Vibration measurement results of the sandwich piezoelectric actuator assembled with the U-shaped preload adjustment mechanism

3.2 最佳预压力测试

在课题组之前的工作中发现，履带靠自身的张紧力与夹心式压电振子的驱动圆环接触，一旦履带移动系统样机工作时间长，履带内表面存在磨损，从而改变了履带与驱动圆环之间的预压力，原理样机的输出性能受到影响，导致系统稳定性下降[16]。因此，开展最佳预压力实验研究对于提高系统的稳定性和工作效率十分必要。预压力调节方法如图9所示，改变金属杆与连接块上表面的距离h以实现履带与压电振子的预压力调节。通过测试金属杆在不同高度位置施加给履带的支撑力，以获得履带和压电振子之间的预压力。通过改变预压力，测试获得了不同预压力下原理样机的最佳工作频率及其对应的最大平均运行速度，如图10所示。两相具有π/2相位差、幅值为300 V的电信号同时施加在原理样机上。在未改变履带和夹心式压电振子之间的预压力时，即预压力由履带自身张紧力确定，金属杆与压电振子连接块上表面的高度距离为7 mm。实验过程中，每一个预压力值的增加意味着金属杆上调高度增加1 mm。实验结果表明，随着金属杆上调高度的逐渐增加，预压力调节结构施加在履带上的支撑力以及原理样机的最佳驱动频率均呈现不断递增趋势，而原理样机的最大平均运行速度则表现为先增加再减小变化趋势。因此，存在一个最佳的支撑力对应原理样机最大的平均运行速度，同时最佳支撑力对应着履带与夹心式压电振子的驱动圆环之间的最佳预压力。当金属杆上调高度为17 mm时，通过测算得到预压力调节机构施加在履带上的支撑力为28.3 N，此时原理样机的最佳驱动频率为34.925 kHz，最大平均运行速度为42 mm/s。

图9 施加在原理样机上的预压力大小测试方法Fig.9 Measured method of the preload applied on the system prototype

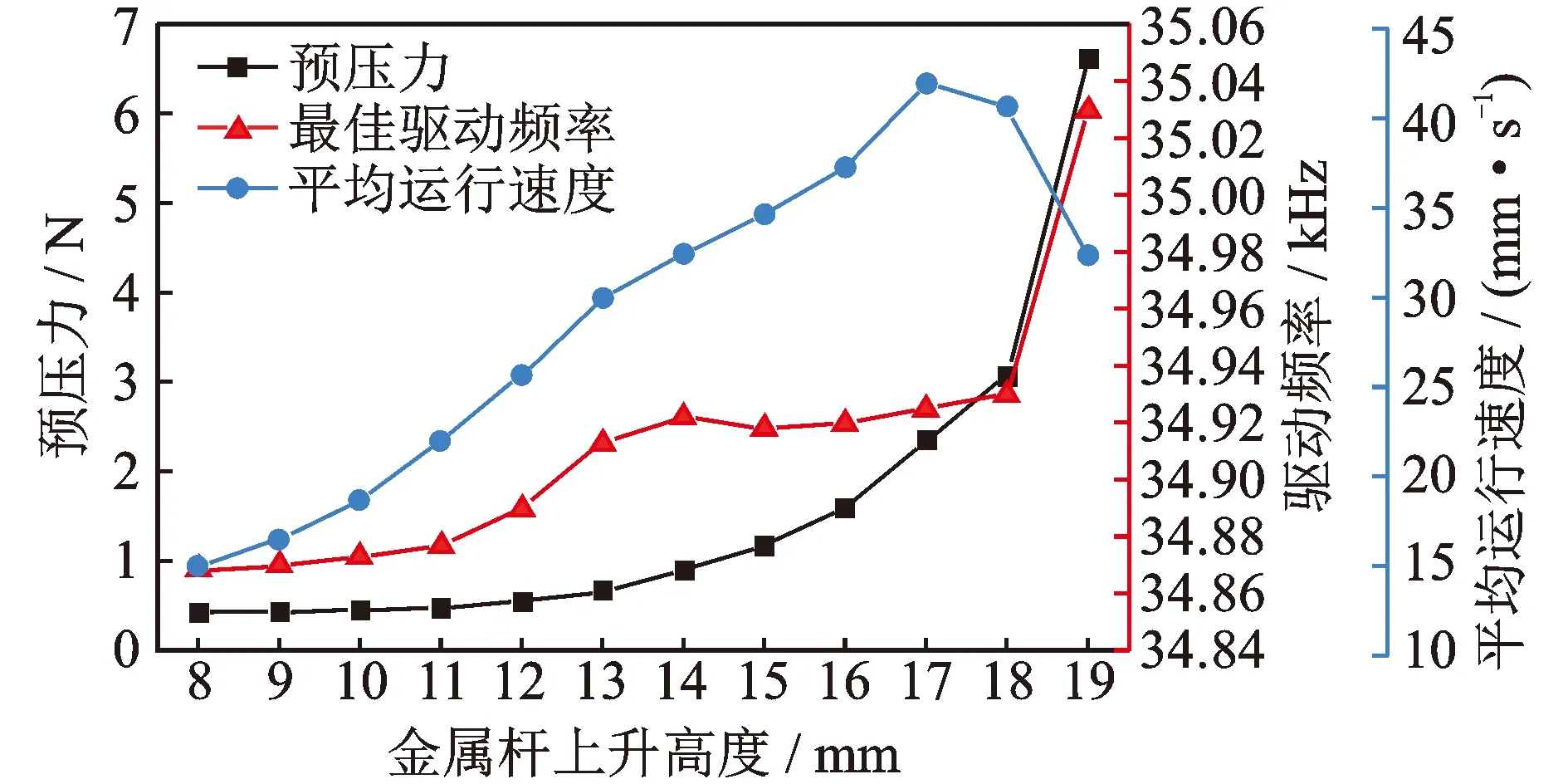
图10 原理样机的预压力特性曲线Fig.10 Preload characteristic curves of the system prototype

3.3 牵引力特性测试

为了进一步评估原理样机在上述最佳预压力情况下的系统输出性能，开展了牵引力特性测试实验研究。为了研究预压力对原理样机输出牵引力的影响关系，进行了原理样机在无预压力调节机构和最佳预压力这两种工作状态下的牵引力特性对比实验。在上述2种预压力状态下，施加在原理样机上的两相激励信号的相位差均为π/2，驱动频率均为原理样机在上述2种工作状态下对应的最佳工作频率。在不同驱动电压下，测试了原理样机在上述2种预压力工作状态下的最大输出牵引力，实验结果如图11所示。随着驱动电压幅值的增加，原理样机在最佳预压力下和无预压力装置2种工作状态下所输出的最大牵引力均呈现线性增加的变化趋势。通过对比两种预压力工作状态下原理样机输出的最大牵引力特性可以看出，在任意相同驱动电压下，原理样机在最佳预压力工作状态下输出的最大牵引力均大于无预压力调节装置工作状态。当驱动电压为400 V时，原理样机在最佳预压力工作状态下的最大牵引力为6 N，而在无预压力调节装置工作状态下的最大牵引力仅为0.578 N。因此，当原理样机工作在最佳预压力工作状态下输出的最大牵引力超过了无预压力调节装置工作状态下的10倍，充分说明在最佳预压力工作状态下，原理样机的输出性能得到了大幅提高。

图11 原理样机在2种预压力状态下的牵引力特性曲线Fig.11 Tractional characteristic curves of the system prototype under two preload states

为了研究原理样机在最佳预压力工作状态下的牵引力与平均运行速度之间的关系特性，开展了相关的实验测试，结果如图12所示。两相激励电压的幅值为250 V，驱动频率为34.925 kHz，相位差为π/2。可以看出，随着原理样机输出的牵引力增加，其平均运行速度逐渐减小。当原理样机的输出牵引力达到3.5N，其平均运行速度小于5 mm/s。

图12 原理样机在最佳预压力状态下的平均运行速度与牵引力之间的关系Fig.12 Relationship between the mean velocity and tractional force of the system prototype under the optimal preload state

3.4 越障性能

为了评估原理样机在最佳预压力工作状态下的越障性能，笔者以原理样机攀爬台阶为例进行了实验研究，如图13所示。两相激励电压的相位差为π/2，幅值为250 V。原理样机攀爬不同斜坡角度台阶的实验结果如图14所示。可以看出，在最佳预压力工作状态下，随着台阶斜坡角度的增加，原理样机所能攀爬的台阶高度值先增加后减小。原理样机攀爬的最高台阶高度为207.8 mm，对应台阶的斜坡角度为60°。当台阶的斜坡角度大于60°时，原理样机的驱动性能难以克服重力所带来的阻力，从而无法再攀爬台阶。实验结果表明，原理样机具有良好的台阶攀爬性能，展示出了作为微小型月面巡视器移动系统的可能性。

图13 原理样机攀爬台阶示意图Fig.13 Schematic of climbing stairs for the system prototype

图14 原理样机在最佳预压力下攀爬台阶的高度与台阶的斜坡角度之间的关系曲线Fig.14 Relationship between the height of the climbed stairs and the slope angle of the stair under the optimal preload

月球表面多处存在沟壑，因而能否跨越沟壑以及最大能跨越的沟壑宽度成为了评估月面巡视器移动系统性能的重要指标。为了测试压电驱动履带移动系统跨越沟壑的能力，开展了最佳预压力工作状态下原理样机在不同驱动电压下跨越沟壑宽度的实验研究。两相电信号的相位差为π/2，驱动频率为原理样机在最佳预压力工作状态对应的频率。原理样机跨越沟壑的实验结果如图15所示。随着驱动电压的升高，原理样机能够跨越沟槽的宽度线性增加。原理样机跨越沟槽的最大宽度为78 mm，所对应的驱动电压为400 V。上述实验结果说明原理样机具有良好的跨越沟槽能力。

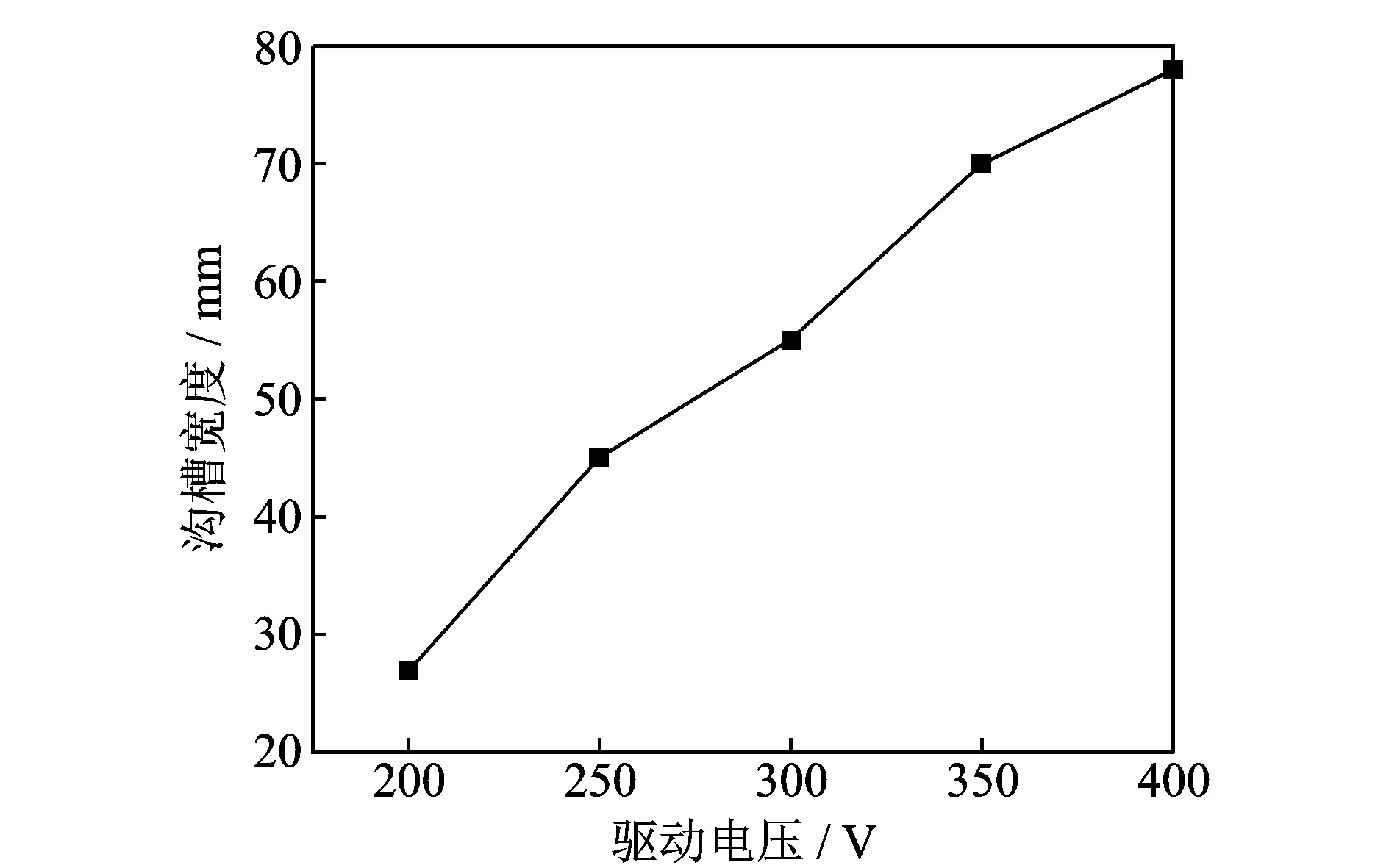
图15 原理样机在最佳预压力状态下跨越沟槽的宽度与驱动电压之间的关系Fig.15 Relationship between the width of crossing the trench and driving voltage under the optimal preload

3.5 模拟月壤环境下的运动速度特性

为了测试压电驱动履带移动系统在月壤/月尘环境下的运动特性，笔者进行了最佳预压力工作状态下原理样机在不同直径的月壤颗粒环境下的实验研究。选取了火山灰(颗粒直径约为0.01 mm)作为月尘以及5种不同颗粒直径的沙粒作为月壤，并且由单一粒径的月壤/月尘构建的工作界面厚度均为5 mm。

当两相幅值为250 V、具有π/2相位差的激励信号施加在原理样机上，实验结果如图16所示。当原理样机分别运行在火山灰工作界面以及直径为0.1，0.8和3 mm 3种沙粒工作界面上，其平均运动速度均超过40 mm/s，由此可以说明由这些尺寸的火山灰和沙粒构建的工作界面对原理样机的运动性能并未产生阻碍作用。当沙粒的直径为0.5 mm和5 mm时，原理样机运行的平均运动速度均低于30 mm/s，说明这两种直径的沙粒对原理样机的运动性能产生了阻碍作用。实验过程中发现，微米尺度的颗粒(火山灰和直径为0.1 mm的沙粒)容易进入到履带与驱动圆环的接触界面，但在超声振动作用会随着履带的运动排出接触界面。虽然微米尺度的沙粒进入接触界面会改变界面的粗糙度，但履带与驱动圆环之间的预压力同时发生改变，因此接触界面产生的摩擦力并未因沙粒的进入而产生波动，保证了原理样机的运动性能不发生较大改变。直径为0.5 mm的沙粒对原理样机的运行性能产生影响的主要原因是由于这种沙粒的直径与履带块之间的间隙大小相近，导致沙粒容易卡在相邻两片履带块之间，改变履了带的柔度，从而影响了原理样机的运行性能。当沙粒直径为0.8 mm和3 mm时，沙粒构建的工作界面适合原理样机运行。因为这2种沙粒的直径已经大于相邻履带块之间的间隙以至于不能影响履带的柔度，并且不能随着履带的运动进入原理样机的接触界面。当原理样机运行在直径为5 mm的沙粒构建的工作界面时，由于沙粒的直径较大，阻碍了履带的运动，致使原理样机的运动性能下降。实验结果表明，夹心式压电驱动履带移动系统能够在月壤和月尘的模拟环境中工作。

图16 原理样机在最佳预压力下的平均运行速度与沙粒直径之间的关系Fig.16 Relationship between the mean velocity and sand diameter under the optimal preload

月球表面分布着多处月壤厚度不一的地带，因此有必要开展原理样机在不同厚度的月壤模拟环境下的实验研究。笔者选取了火山灰和3 mm粒径的沙粒构建的不同厚度的沙堆作为原理样机运行的月壤模拟环境。驱动电压的幅值为250 V，驱动频率仍为原理样机在最佳预压力工作状态下的频率。在上述两种月壤模拟环境下，原理样机的运动情况如图17所示。可以看出，沙堆厚度以5 mm的间隔从5 mm增加到25 mm，原理样机在上述两种模拟月壤环境中的运行速度波动较小，说明模拟月壤厚度对原理样机的运行性能影响较小。

图17 原理样机在最佳预压力下的平均运行速度与沙堆高度之间的关系曲线Fig.17 Relationships between the mean velocity and height of sand pile under the optimal preload

4 结 论

1) 通过预压力调节实验研究发现，原理样机存在最佳预压力使得系统的平均运行速度最大。

2) 在最佳预压力的工作状态下，对原理样机进行了牵引力特性实验研究，结果表明：在相同驱动电压下，原理样机在最佳预压力工作状态下输出的牵引力均优于无预压力装置的情况下输出的牵引力。

3) 在最佳预压力的工作状态下，对原理样机进行了越障性能测试，结果表明：原理样机攀爬的最大台阶高度为207.8 mm，跨越的最大沟槽宽度为78 mm。

4) 在最佳预压力的工作状态下，对原理样机进行了模拟月壤环境下的运动特性实验。结果表明，原理样机能够在不同粒径的模拟月壤上平稳运行。实验结果充分表明，通过改变原理样机的预压力可以有效提升系统的机械输出性能。