基于哑变量的闽楠人工林单木树高曲线模型

颜佳睿，李际平，曹小玉，唐 涛，孙 宇，王奕茹

（中南林业科技大学 林学院，湖南 长沙 410004）

闽楠Phoebe bournei为中国特有植物，俗称楠木，是国家II 级珍稀渐危树种。闽楠主要分布于我国南方地区，多生长于海拔1 000 m 以下的常绿阔叶林中，在我国湖南祁阳金洞林场有一定面积的闽楠人工林和闽楠混交林。闽楠树干高大通直，木材芳香耐久，纹理结构美观，不但具有极高的经济价值，被称为“木中金子”，而且具有涵养水源、保持水土的功能。由于闽楠苗木死亡率较高、生长特别缓慢、人为砍伐和自然环境改变等因素造成濒危。目前对于闽楠人工林的林分生长规律研究并不多见，且缺乏长期监测与动态调查。仅有部分学者对闽楠的林分生长规律进行了研究，王文意[1]和刘宝[2]等人对闽楠人工林生长规律进行了研究；石乐[3]基于解析木数据构建了闽楠人工林生长模型；曹梦[4]基于哑变量构建了闽楠天然次生林单木胸径和树高生长模型；李琪媛[5]构建了杉木-闽楠混交林单木生长模型，但目前对于闽楠生长规律的探究仍然不多。

胸径和树高作为野外调查的重要调查指标[6]，也是森林质量、林木蓄积量鉴定、森林生长、采伐和立地指标评价的重要依据。同时，与胸径相比，树高在野外测量中，由于树冠重叠，所以导致测量难度较大，精度不高[7]。而胸径调查数据精准且易得，不会因树冠遮蔽造成人为测量误差。因此，通常根据一些精确测量的树高和胸径数据建立的回归模型来估计其他树的树高[8-10]，从而可以节约数据调查成本。

树高和胸径之间的关系通常又受到树种结构、立地条件等其他条件的影响，所以在不同树种之间由于林分和立地条件的不同而导致树高-胸径的关系存在较大差异[11]。近年来，普通树高曲线模型已经广泛的使用在林业实践与生产中[12-13]，但是，普通树高-胸径关系模型无法有效地反映不同立地类型下的树高、胸径生长差异[14-15]。通过哑变量可以解决相应的区域性的问题[16-19]，因此，建立立地类型哑变量的闽楠人工林单木树高曲线模型，对于研究闽楠人工林的生长预估和收获具有重要意义。

以湖南省金洞林场闽楠人工林为研究对象，通过固定样地获取闽楠数据，选取应用较为广泛的树高曲线模型作为基础模型，得出最适基础模型。考虑到不同立地类型对树高、胸径生长有影响，建立以立地类型为哑变量的单木树高曲线模型，以此探索闽楠人工林的生长规律，为金洞林场闽楠人工林的目标树经营和生长预估提供理论依据。

1 研究区概况

金洞林场位于湖南省永州市祁阳县南部，湘江支流白水河上游，南岭余脉的东北部，26°21′10″～26°21′37″N，110°53′43″～112°13′37″E 之 间，东西宽约33 km，南北长约36 km，总面积635 km2。金洞林场属中亚热带东南季风湿润气候区，年平均气温16.3～17.7 ℃，极端最高气温40 ℃，极端最低气温-8 ℃。年降水量约为1 600～1 900 mm，年蒸发量约1 225 mm。年有效日照时数1 617 h，相对湿度75%～82%，全年无霜期260～344 d，植物生长期280～300 d。最高海拔1 435 m，位于白果市乡与大江林场交界处的雄霸岩主峰，最低海拔108 m。林区土壤以黄红壤和山地黄壤为主，海拔1 000 m 以上为山地黄棕壤，丘陵地区以红壤为主，土层厚度一般在60 cm 以上，土壤较疏松，通气良好，质地轻至中壤，石砾含量一般在20%～30%，土壤有机质含量平均在2%以上，最高达11%。土壤微生物小循环非常明显，有利于形成树木生长所需的养分。

金洞林场植物资源丰富，共有135 科972 种。主要木本植物90 科、290 属、794 种；其中：具有栽培价值的210 种，特用经济价值的25 种，速生树种30 多种。目前尚存的国家重点保护的Ⅰ级植物伯乐树Bretschneidera sinensis、银杏Ginkgo biloba等；国家Ⅱ级保护植物有闽楠Phoebe bournei、福建柏Fokienia hodginsii、篦子三尖杉Cephalotaxus oliveri、花榈木Ormosia henryi、厚朴Magnolia officinalis等。

2 材料与方法

2.1 数据来源

以金洞林场闽楠人工林为研究对象，通过对金洞林场内所有闽楠人工林的全面勘察基础上，共设置了18 块闽楠人工纯林固定样地，其中600 m2（20 m×30 m）样地有15 块，400 m2（20 m×20 m）有3 块。并在2015年至2019年对样地进行每木检尺，本研究数据调查的起止时间为2017年8月到2019年8月。固定样地基本情况详见表1。

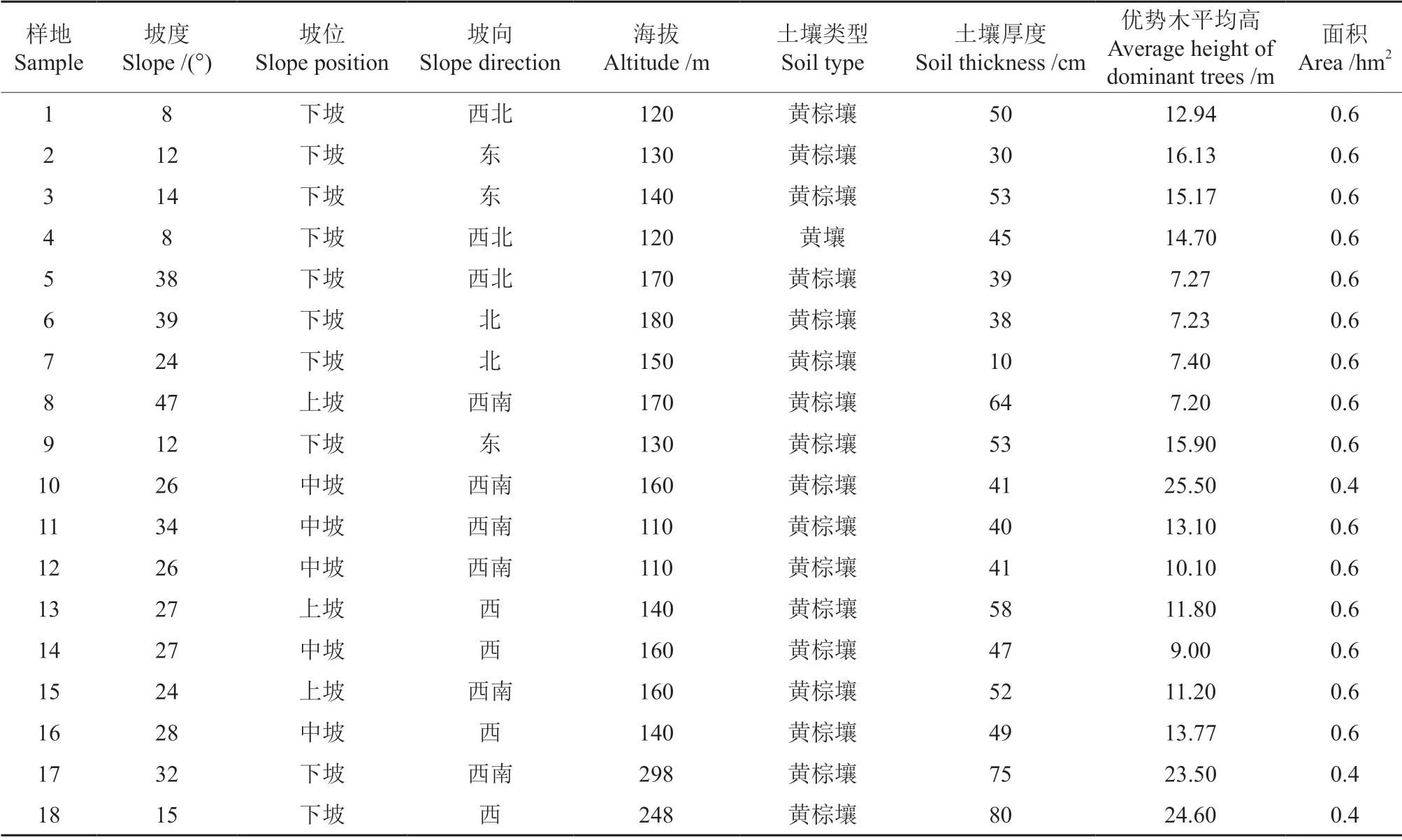
表1 固定样地基本情况Table 1 Basic information of fixed sampling plots

对闽楠人工林经营历史和经营措施进行相应了解和调查，所有样地都采用相邻网格法以10 m作为标准，把样地分隔成若干个10 m×10 m 的小样方作为调查单元，对样地内达到起测径胸径5 cm的闽楠进行每木检尺，通过中林遥软件记录样地的地理位置、经纬度、坡位、坡度、坡向，对土壤进行取样，了解土壤类型、土壤厚度。记录每株树木的坐标(x,y)、胸径、树高、东西冠幅、南北冠幅等基本因子。调查生活力，干形质量，林木等级等生长评价因子。对林场资料整理，获得林分起源、林龄。

本数据来源为金洞林场固定样地2019年实测数据，闽楠人工林样地共计18 块样地611 个单株木数据。所有建模数据如表2所示。

2.2 研究方法

2.2.1 立地类型划分

采用Forstat2.2 软件中的“数量化方法Ⅰ”，将样地内的3 株优势木树高平均值作为因变量，以坡度、坡位、坡向、海拔、土壤类型和土壤厚度这几类立地因子和林分年龄为自变量，通过对以上立地因子的显著性进行分析，筛选出显著性影响因子。为了便于知道金洞林场的经营，对显著性影响因子进行等级划分后，对样地进行聚类分析划分立地类型。

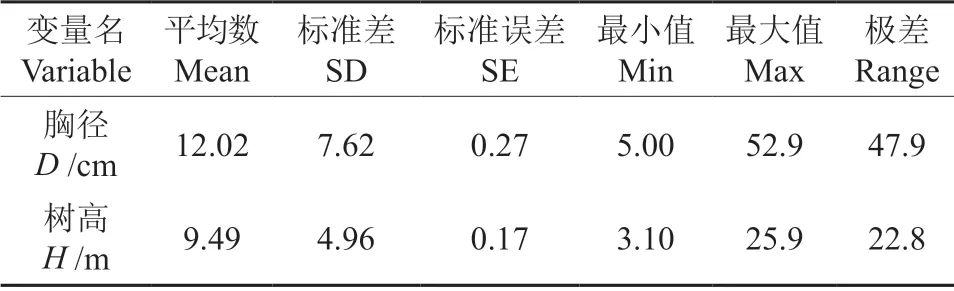
表2 建模数据统计Table 2 General situation of sample data

2.2.2 基础模型选择

目前国内外对于树高曲线模型研究十分广泛，同时有线性模型和非线性模型，树高曲线又称树高曲线模型，本研究中采用最常见的11 种应用较为广泛的树高曲线作为研究闽楠人工林树高与胸径关系的基础模型进行拟合，模型形式如表3所示。

表3 基础模型†Table 3 Foundation models

2.2.3 哑变量设置

哑变量，又称虚拟变量[20-21]，是对等级性（定性）数据x，用变量d（x,i）表示成关于定性因子的（0,1）展开，即关于d（x,i）=（d（x,1），d（x,2），...d（x,m）），其中一个定性变量（m个等级）对应一个向量，一个定性变量就变成可以进行数值运算的数值向量。根据立地类型划分结果，以立地类型做为哑变量，并利用定性代码ki表示不同立地类型，将定性数据ki转化为（0,1）：

式中：i=1,2,...,m。

2.2.4 模型精度检验

模型精度检验采用决定系数（R2）、均方根误差（RMSE）、平均绝对误差（MAE）3 个指标对模型进行评价，当决定系数（R2）越大，代表模型精度越高，均方根误差（RMSE）、平均绝对误差（MAE）越小代表模型精度越高，拟合效果越好。

3 结果与分析

3.1 立地类型划分结果

使用ForStat 2.2 软件中的“数量化方法Ⅰ”，取3 株优势木树高的平均值作为因变量，以定性因子坡位、坡向、土壤类型；定量因子坡度、海拔、土壤厚度和林分年龄为自变量，对以上立地因子进行显著性分析。通过对方差分析表中各因子的“Pr＞F”值分析，当“Pr＞F”值小于0.05 时，则可以认为该因子对林分优势高影响显著，剔除不显著因子后重复进行显著性分析。

由表4筛选结果可得，对林分优势高影响显著的主要立地因子为坡向和海拔，由表1可知金洞林场所有闽楠人工林固定样地分布中，不存在坡向为阳坡（即南坡）的情况，且海拔基本处在300 m 以下，可通过对显著因子坡向、海拔进行等级划分，划分结果详见表5。

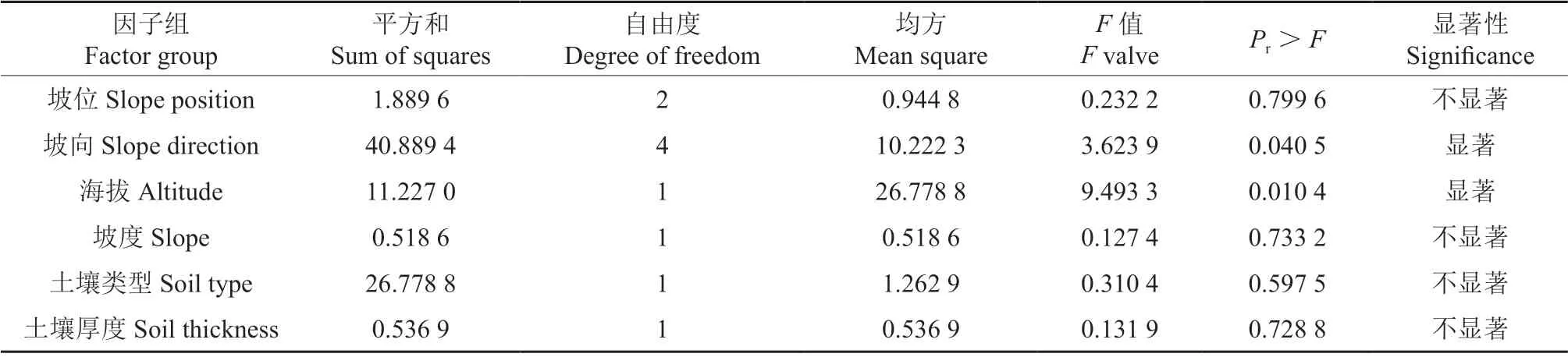
表4 立地因子显著性检验Table 4 Site factor significance test

表5 显著因子等级划分Table 5 Classification of significance factors

为便于更好地分类经营和添加哑变量，采用离差平方和法将立地类型进行聚类，恰好将18 块样地划分为3 个主要立地类型，编号和数量详见表6。

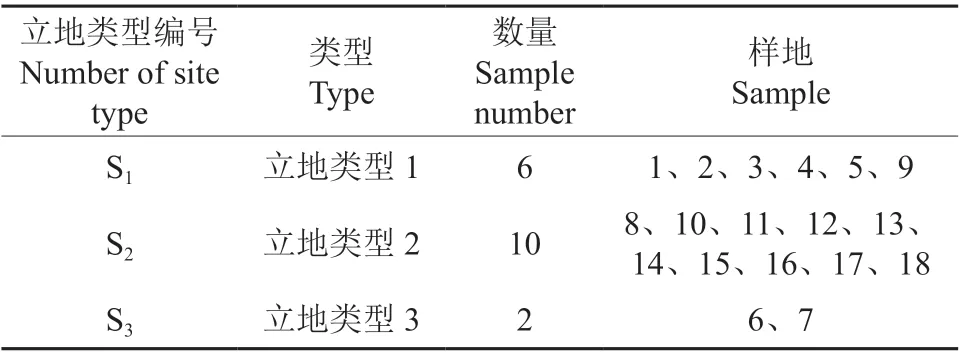
表6 主要立地类型编号和数量Table 6 Main site type number and quantity

3.2 基础模型拟合结果

预测和研究金洞林场闽楠人工林的生长规律，基于实测的树高-胸径数据，通过比较分析11 个基础模型。用ForStat 2.2 中的非线性回归模型拟合了11 个备选模型，并对其参数进行了估计，楠木共计611 组数据。闽楠人工林树高-胸径基础模型拟合结果如下表7所示。

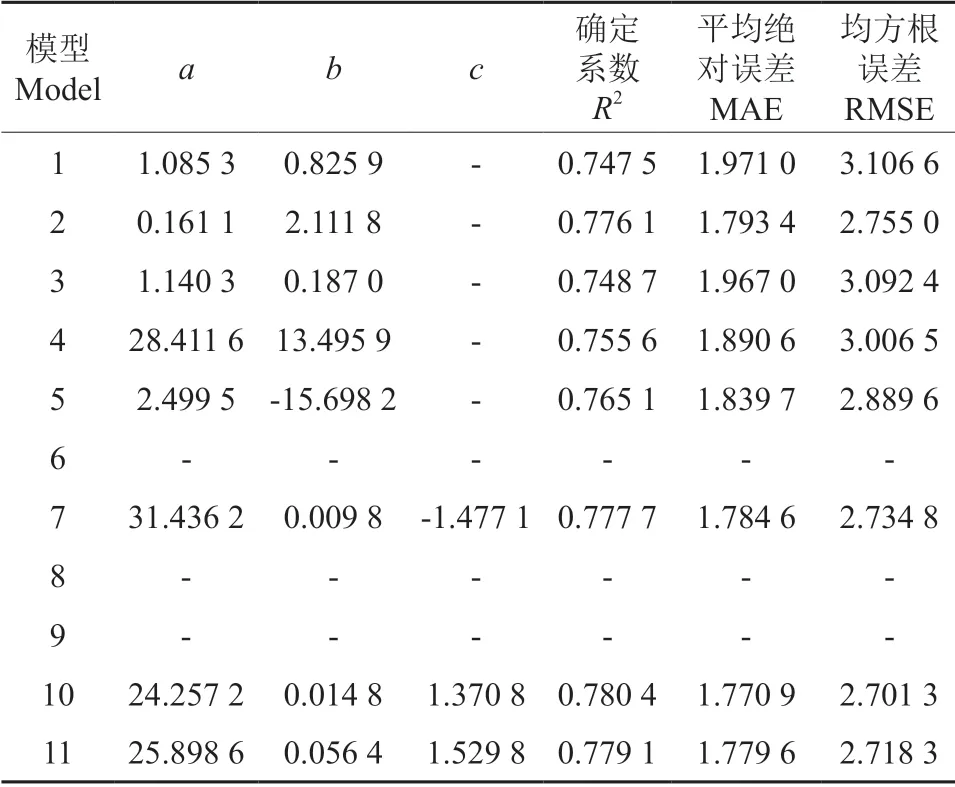
表7 楠木基础模型拟合结果Table 7 Fitting results of candidate models

由表7可以看出，11个方程中除了Strand模型、Ratkowsky 模型、Pearl,Reed 模型不收敛外，其他8 个树高曲线的决定系数在0.747 5～0.780 4 之间，平均绝对误差（MAE）在1.770 6～1.971 0 之间，均方根误差（RMSE）在2.701 3～3.106 6 之间。由此可知表7中不同的方程拟合效果差异并不大，但是三参数的树高曲线模型的拟合精度普遍高于两参数的树高曲线模型，平均绝对误差和均方根误差相比更低。其中Weibull 方程的拟合效果最佳，其决定系数（R2）为0.780 4 最大，平均绝对误差（MAE）为1.770 9 与均方根误差（RMSE）为2.701 3最小，所以选择Weibull方程作为模拟单木闽楠树高-胸径生长的基础模型，其模型的形式为：

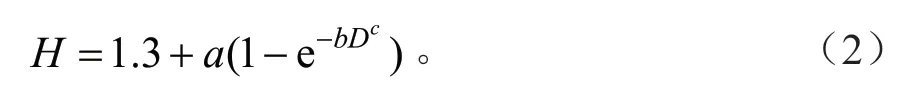
式中：D为单木胸径，H为单木树高，a、b、c为模型参数。

3.3 哑变量模型拟合结果

选出闽楠人工林树高-胸径拟合效果最好的模型作为基础模型，使用Forsata2.2 的非线性回归模块，将立地类型作为哑变量，加在最优基础模型Weibull 方程中的不同参数（a；b；c；a、b；a、c；b、c；a、b、c）上拟合，得出哑变量添加在参数值较大的a；c；a、c上拟合结果可信，不存在不收敛的情况，最为稳定，并通过决定系数、MAE、RMSE 来选择最优哑变量参数组合。

3.3.1 将哑变量添加在参数a 上

模型表达式为：

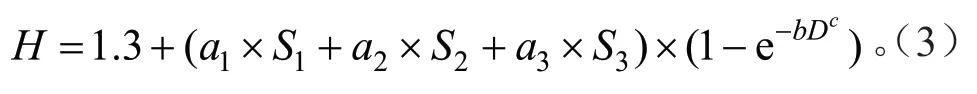
式中：D为单木胸径，H为单木树高，a1、a2、a3、b、c为模型参数，S1、S2、S3为立地类型。通过模拟，模型的决定系数为0.811 2，平均绝对误差（MAE）为1.603，均方根误差（RMSE）为2.322 3。拟合结果如表8所示：

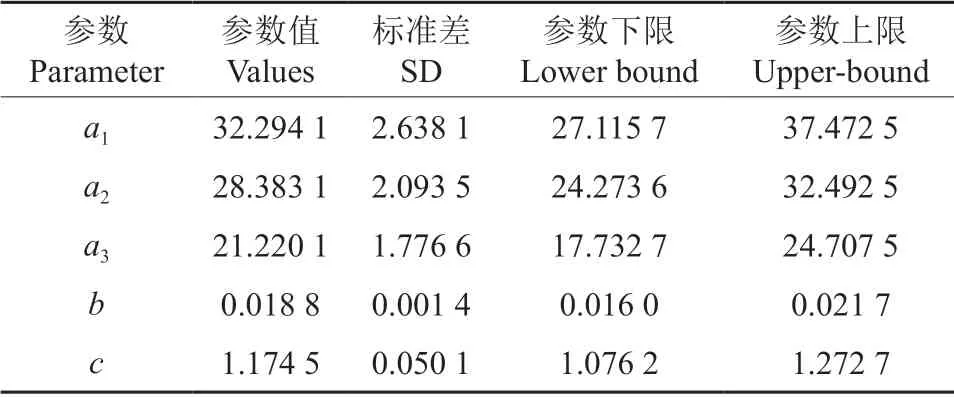
表8 哑变量添加在a 上的参数Table 8 Parameters of dummy variable added to a

3.3.2 将哑变量添加在参数c 上

模型表达式为：

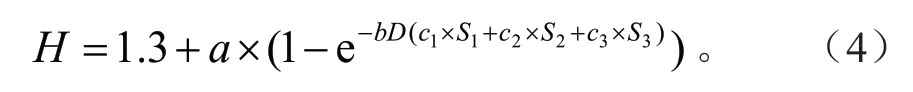
式中：D为单木胸径，H为单木树高，a、b、c1、c2、c3为模型参数，S1、S2、S3为立地类型。通过模拟，模型的决定系数为0.834 9，平均绝对误差（MAE）为1.529 5，均方根误差（RMSE）为2.131 6。拟合结果如表9所示。

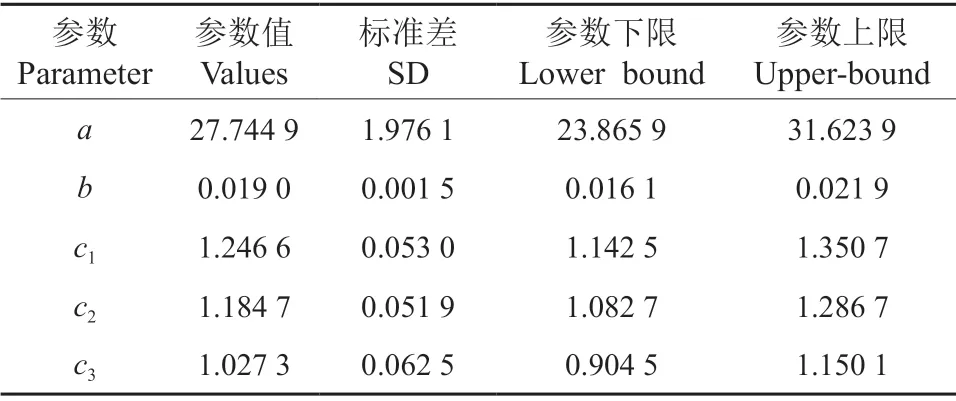
表9 哑变量添加在c 上的参数Table 9 Parameters of dummy variable added to c

3.3.3 将哑变量添加在参数a、c 上

模型表达式为：

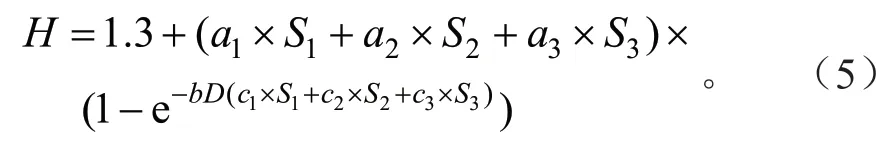
式中：D为单木胸径，H为单木树高，a1、a2、a3、b、c1、c2、c3为模型参数，S1、S2、S3为立地类型。通过模拟，模型的决定系数为0.811 6，平均绝对误差（MAE）为1.595 6，均方根误差（RMSE）为2.317 6。拟合结果如表10所示：

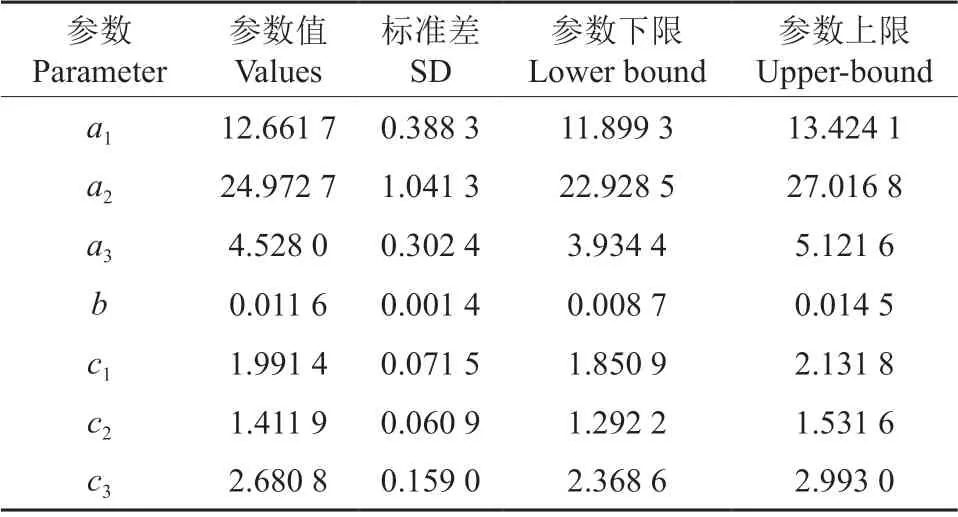
表10 哑变量添加在a、c 上的参数Table 10 Parameters of dummy variable added to a and c

3.3.4 最佳单木闽楠树高曲线模型

由表11可知，通过在Weibull 方程上添加哑变量，所获得的3 个哑变量模型精度均优于基础模型。3 个哑变量模型中，哑变量添加在参数c 上的模型4 精度优于其他两个模型。最优模型4 相比于基础模型2 来说，决定系数提升了6.98%，平均绝对误差（MAE）降低了13.6%，均方根误差（RMSE）降低了26.7%。由图1所示，最优模型4 的残差为随机分布，未出现显著的异方差，因此不考虑对模型消除异方差。

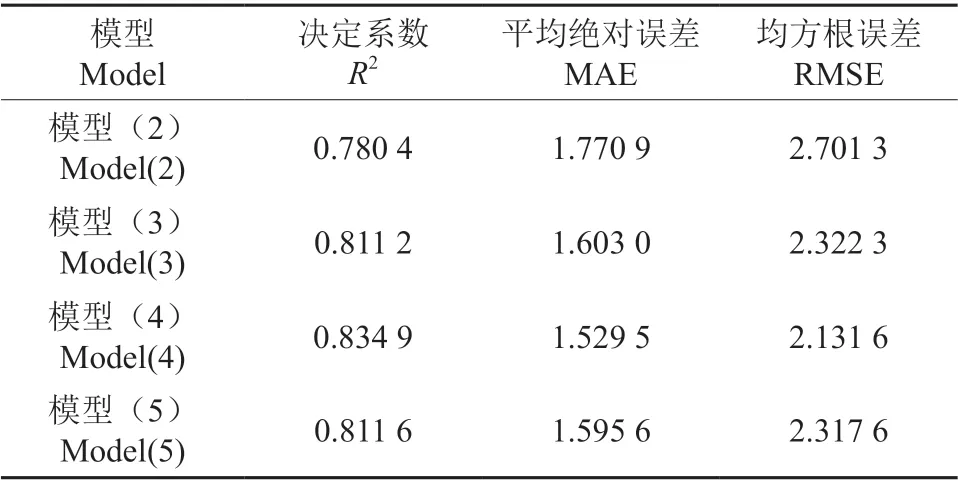
表11 基础模型与哑变量模型精度对比Table 11 Accuracy comparison between basic model and dummy variable model

综上所述，最终闽楠单木树高曲线模型表达式为：

式中：D为单木胸径，H为单木树高，S1、S2、S3为立地类型。

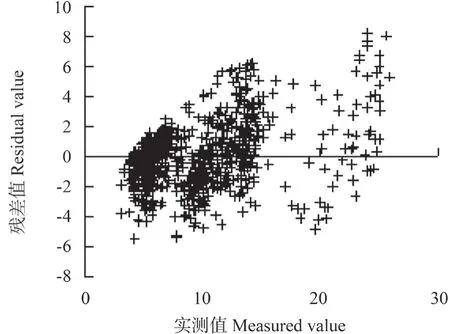
图1 残差分布Fig.1 Residual distribution

4 结论与讨论

4.1 结 论

本研究通过用金洞林场18 块固定样地的2019年实测数据为基础，构建了闽楠人工林单木树高-胸径关系模型，并构建了立地类型哑变量模型得到如下结论：

1）基于实测数据，采用11 个候选基础模型进行拟合，11 个方程中除了Strand 模型、Ratkowsky 模型、Pearl，Reed 模型不收敛外，其余8 个基础模型对单木树高-胸径关系的拟合精度都在0.747 5～0.780 4 之间，平均绝对误差在1.770 6～1.971 0 之间，均方根误差在2.701 3～3.106 6 之间。其中Weibull 方程拟合效果最好：H=1.3+a(1-e-bDc)，决定系数为0.780 4 最大，平均绝对误差（MAE）为1.770 9，均方根误差（RMSE）为2.701 3 最小。

2）将立地显著因子分级并聚类后，划分出的立地类型做为哑变量，添加在Weibull 方程的3 个参数7 种形式上，得出添加在b；a、b；b、c；a、b、c上拟合结果不可信或不收敛，得出添加在a；c；a、c上拟合结果可信，且不存在不收敛的情况。将构建的3 个哑变量模型和基础模型进行比较，决定系数提高了3.95%～5.45%，MAE降低了0.167 9～0.241 4，RESE 降低了0.379 0～0.569 7，说明3个哑变量模型普遍优于基础模型。

3）构建的3 个哑变量模型中，哑变量添加在参数c上的模型4 精度优于其他两个模型，模型形式为：H=1.3+27.744 9×(1-e-bD(0.019×S1+1.1847×S2+1.0273×S3))，决定系数为0.834 9，平均绝对误差（MAE）为1.529 5，均方根误差（RMSE）为2.131 6。对比于基础模型，确定系数提升了6.98%，平均绝对误差（MAE）降低了13.6%，均方根误差（RMSE）降低了26.7%。说明含立地类型哑变量模型的拟合效果较好，有更强的适用性，可以为湖南省金洞林场闽楠人工林的目标树经营和生长预估提供理论依据。

4.2 讨 论

1）本研究基于金洞林场2019年实测数据，由于闽楠样地不多，观测年龄不够全面，以至于模型精度不够高，需要在日后继续对闽楠人工林继续进行观测以便获得更加精准和全面的数据。并且该套模型只针对于金洞林场闽楠人工林的生长预测，不适用于其他地域条件下的闽楠生长过程，应用于其他地域条件下的闽楠生长可能会出现预估值过高的情况。

2）本研究基于筛选出显著的立地因子，并以此为依据将立地进行组合与聚类，同时作为哑变量添加在模型参数上。部分学者曾在建模时采用除立地类型以外的其他哑变量，如林分类型、竞争指数等，今后也可以尝试采用相关哑变量建模预估闽楠的生长。

3）本研究采用单株木数据进行建模，但被压木数据也可能在单木数据中，以至于建模精度不高。在今后的研究中可以参考其他学者建立的以优势木数据为基础的树高曲线模型，提高模型精度。