华北落叶松与白桦混交林树高与胸径关系研究

王冬至，刘红艳，张冬燕，b，宋晓彤，徐安阳，李 静

（河北农业大学 a.林学院；b.经济管理学院，河北 保定 071000）

树高和胸径是森林资源调查工作中最重要的两个观测因子，不仅是构建森林生长与产量模型的基础变量[1-2]，而且在预测林分结构[3]、材积分布以及蓄积量[4-5]等研究中具有重要意义。Vargas等[6]研究表明，相比树高而言胸径的观测不仅快速、准确，并且观测成本较低，而树高的观测则耗时耗力且费用较高[7]。因此，在森林资源调查工作中，通常对样地内所有立木胸径进行实测，通过树高与胸径关系模型来预测样地内树高，从而在满足预测精度前提下可降低调查成本[8-9]。

目前，国内外许多学者[10-15]大都基于不同形式线性和非线性模型来研究不同林分类型树高与胸径关系预测模型，其中非线性模型能够更好地描述树高与胸径的关系[13，15]。最初树高与胸径关系模型中仅包含胸径一个自变量[16-17]，随着林龄的增加，树高与胸径关系通常会受到多种林分因子及立地因子的影响[18]。为了提高模型预测精度及适用性，Sánchez 等学者[19-21]在研究中加入了立地因子、林分因子及环境因子，构建了包含不同变量及变量组合的树高与胸径关系模型。然而这些模型大都基于最小二乘法来估计模型参数[10,22]，在研究中由于调查数据经常会存在观测误差、时间相关性和空间异质性[3,23-24]，导致模型在应用过程中产生较大预测误差，而非线性混合效应不仅能有效解决这些问题，而且在应用过程中具有更好的灵活性[22-23]。Sharma 等学者[15,25-26]研究杉木纯林和油松纯林树高与胸径关系时，表明固定效应模型预测及拟合精度均低于混合效应模型。当前，大多数学者均基于非线性混合效应模型来构建纯林树高与胸径关系模型，然而针对多树种、结构复杂的针阔混交林，如何基于主要影响因子来构建不同树种树高与胸径关系的模型研究较少。因此，基于非线性混合效应模型构建针阔混交林不同树种树高与胸径关系模型具有重要意义。

在研究多树种树高与胸径关系模型中，通常采用哑变量[20]来解决树种效应对模型预测精度影响，Eerikäinen 等[27]研究表明包含哑变量预测模型比分树种建立模型具有更好的预测效果。因此，本研究以河北省塞罕坝华北落叶松Larix principisrupprechtii与白桦Betula platyphylla针阔混交林为研究对象，首先基于候选树高与胸径关系模型，确定能够描述树高与胸径关系的最优基础模型；其次通过相关性分析确定影响树高生长主要因子；最后基于最优候选模型和主要因子，构建包含哑变量的多树种非线性树高与胸径关系混合效应模型，为多树种混交林立地质量评价及森林可持续经营提供科学依据。

1 研究区概况

河北省塞罕坝机械林场（41°22′～42°58′N，116°53′～118°31′E）位于河北省最北部，地势北高南低，处于阴山山脉与大兴安岭余脉的交接地带，属华北暖温带立地类型区，林场总面积约为9.2×104hm2，总蓄积约为8.1×106m3。研究区海拔在1 010～1 940 m 范围内，年均气温-1.2 ℃，年均最高气温33.4 ℃，年均最低气温-43.3 ℃；年均降水量约452.2 mm，年均蒸发量1 339.2 mm；土壤类型主要以褐色森林土、棕色森林土、砂壤土、壤土、风沙土为主。研究区主要乔木树种包括华北落叶松、白桦、蒙古栎Quercus mongolica、樟子松Pinus sylvestris、云杉Picea asperata、山杨Populus davidiana、棘皮桦Betual davurica等，主要灌木树种有胡枝子Lespedeza bicolor、绣线菊Spiraea salicifolia、稠李Prunus padus、忍冬Lonicera japonica等，草本植物主要有曼陀罗Datura stramonium、地榆Sanguisorba officinalis、唐松草Thalictrum aquilegifolium、歪头菜Vicia unijuga、铁线莲Clematis florida、紫斑风铃草Campanula punctata、风毛菊Saussurea japonica等。

2 研究方法

2.1 数据来源

研究数据源于2015—2018年华北落叶松与白桦针阔混交林（华北落叶松为人工栽植、白桦为天然更新）标准地调查数据，在河北省塞罕坝机械林场下属的阴河、第三乡、北曼店和大唤起四个分林场，共设置华北落叶松与白桦针阔混交林标准地83 块（30 m×30 m）。在样地内对海拔、土壤质地、土层厚度、坡位、坡度、坡向等立地因子进行观测，并对样地内胸径≥5 cm 立木进行每木检尺，共调查立木3 586 株（白桦1 698 株，华北落叶松1 888 株）。研究过程中，分树种将观测数据分别按3∶1 比例分为建模数据（62 块标准地）和检验数据（21 块标准地），数据基本信息如表1、表2所示。

2.2 基础模型选择

当前有近百种适用于不同林分类型的树高与胸径关系预测模型表达式[28]，本研究根据以往学者[16，28-31]的研究结果，选择了5 个应用范围较广且具有生物学意义的候选树高-胸径模型（表3），作为研究华北落叶松与白桦针阔混交林树高与胸径关系模型的基础模型。

表2 模型检验数据Table 2 Data of test model

表3 树高与胸径基础模型Table 3 Basic model of height-diameter function

2.3 非线性混合效应模型

树木在生长过程中，树高与胸径关系通常会受到多种因子影响[10,32]，研究中采用非线性混合效应建模技术[30-35]来构建混交林中不同树种树高与胸径关系模型，混合效应模型一般形式可表示为：

式（1）中：yijk为第i个样地中第j个树种的第k株立木树高值，M是样地水平分组数量，Mi是样地水平内树种分组数量，nij为第i个样地第j个树种株数，f为包含参数向量ψijk和变量xijk的非线性胸径-树高曲线模型，eijk为误差项，β为固定效应参数向量，Aijk、Bi,jk、Bijk分别为β、bi、bij的设计矩阵，μi、μij分别为第i个样地中第j个树种随机效应，ψ1、ψ2分别为μi、μij的方差-协方差矩阵且为正态分布，Rij为第i个样地中第j个树种的方差-协方差矩阵。

非线性混合效应模型中内方差-协方差残差效应由包括相关因子和加权因子的矩阵Rij来平衡误差，其误差项方差-协方差矩阵结构如公式（2）所示。

式（2）中：Gij为描述异构方差的nij×nij对角阵；Gij为误差自相关矩阵nij×nij；s2为误差扩散的比例因子即模型剩余方差值[35]。

本研究中构建树高与胸径非线性混合效应模型，采用广义正定矩阵表示随机效应的方差-协方差矩阵（D），样地及混角比方差-协方差随机效应矩阵结构如公式（3）所示。

式（3）中：为样地间随机效应参数方差；为不同混交比随机效应参数方差；s1s2和s2s1为随机效应参数协方差（s1s2=s2s1）。

2.4 模型检验与评价

研究中基于模型确定系数（R2）、绝对误差（Bias）、均方根误差（RMSE）、赤池信息准则（AIC）及贝叶斯信息准则（BIC）对模型拟合结果进行检验与评价。R2越大，绝对误差、均方根误差、赤池信息准则及贝叶斯信息准则越小表明模型拟合精度越高。

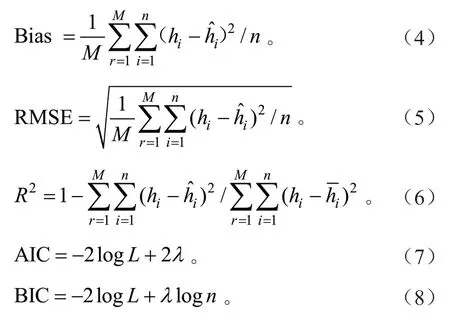
式（4）～（8）中：n为样地中第r个树种的第i株树；n为样地数；hi为树高观测值（m）；为树高预测值（m）；为林分平均树高（m）。

3 结果与分析

3.1 基础模型拟合与评价

在华北落叶松与白桦针阔混交林中，华北落叶松是优势树种且为经营目的树种，因此研究中根据华北落叶松拟合结果来确定构建华北落叶松与白桦混交林基础模型。候选模型拟合结果及评价指标如表4所示，其中Richard (M5)模型拟合效果较好，其确定系数（R2=0.918 6）最高，均方根误差（RMSE=2.405 8）以及绝对误差（Bias=0.194 5）最小，因此选择Richard 模型作为本研究基础模型。

表4 基础模型拟合与评价Table 4 Basic model fitting and evaluation

3.2 相关性分析

主要林分因子（密度、优势种断面积、林分总断面积）与立地因子（海拔、坡度、土层厚度）和树高Pearson 相关性分析如表5所示，其中海拔和林分总断面积与树高生长在P＜0.05 水平上存在显著相关性，因此将海拔和林分总断面积作为主要影响因子来构建华北落叶松与白桦树高曲线，从而提高模型预测精度及适用性。

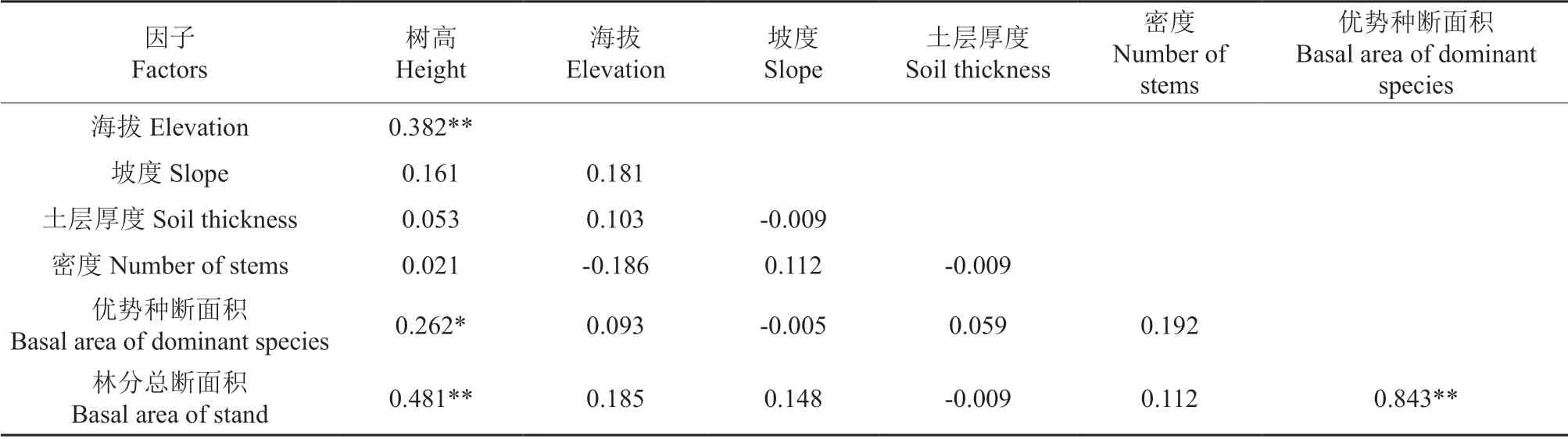
表5 相关性分析†Table 5 Correlation analysis of different factors

3.3 非线性混合效应模型构建与评价

利用拟合精度较高的树高与胸径关系模型（Richard），基于逐步回归分析和方差膨胀因子检验，最终确定林分总断面积及海拔是影响树高主要因子，因此将这两个因子加入基础模型参数a中，生长速率参数b与形状参数c受林分总断面积及海拔影响较小，那么基于哑变量构建的包含林分总断面积及海拔的针阔混交林树高与胸径关系模型可以表示为：

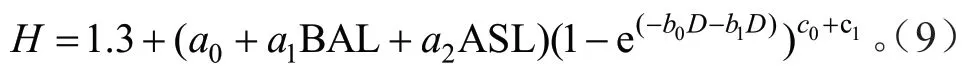
式（9）～（11）中：a0、a1、a2为模型参数；bi和ci为哑变量，当b0=0，b1=1，c0=0，c1=1 为白桦，当b0=1，b1=0，c0=1，c1=0 为华北落叶松；BAL为林分断面积（m2/hm-2）；ASL 为海拔（m）；μ1、μ2是随机效应参数。

基于主要因子构建包含哑变量的树高与胸径关系非线性混合效应模型拟合结果及评价指标如表6～7 所示。随机效应树高与胸径关系模型拟合精度高于固定效应模型，随机效应作用于林分断面积拟合精度高于随机效应作用于海拔，其模型确定系数、均方根误差和绝对误差分别为：0.948 6、2.165 7、0.062 6。基于最优模型对不同树种预测残差进行了分析（图1），各树种残差均不存在异方差现象，表明模型具有较好预测效果。研究中，当随机效应同时作用在海拔和林分断面积上时，模型不收敛。

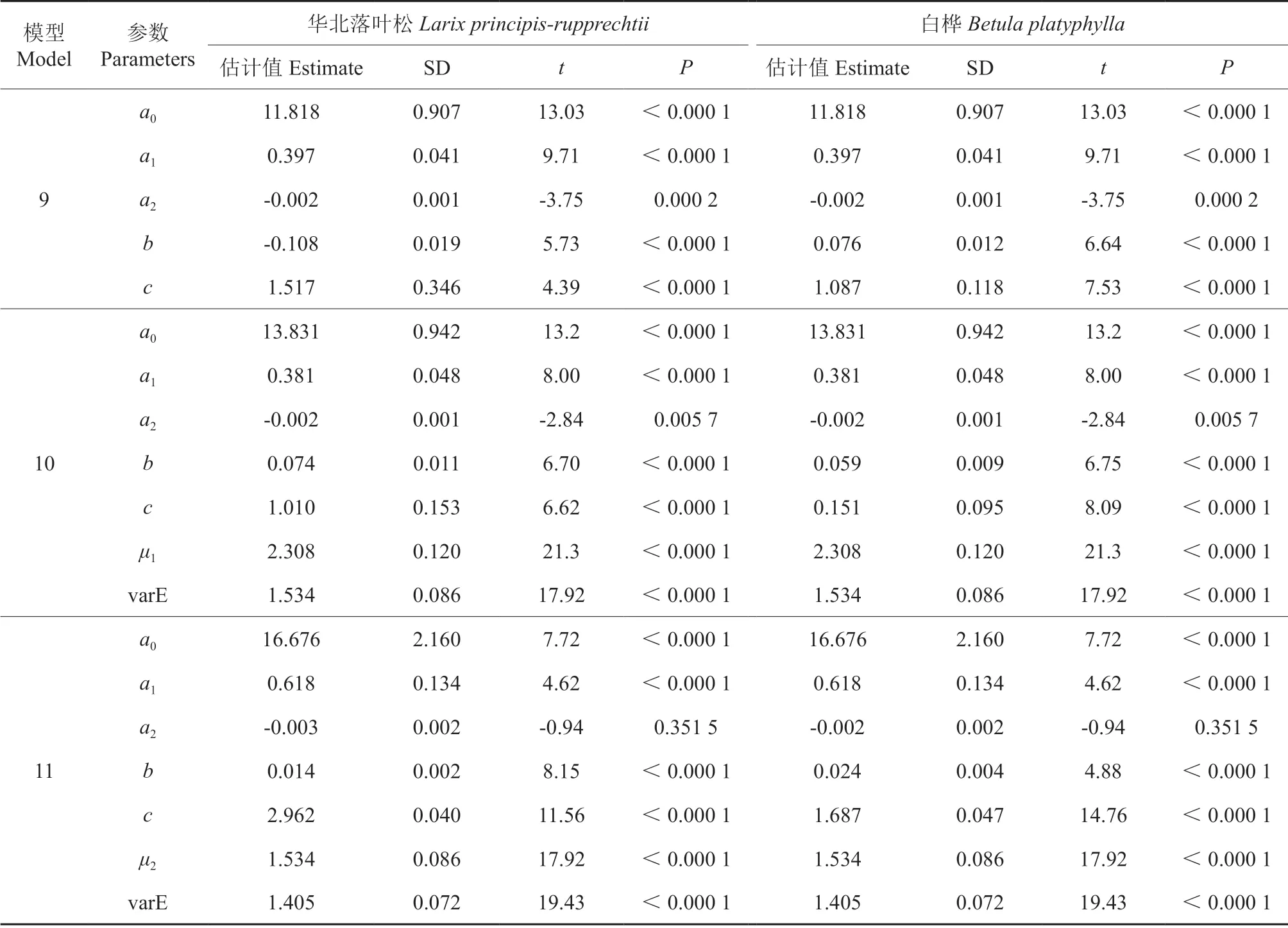
表6 非线性混合效应模型参数估计Table 6 Parameters estimation of nonlinear mixed effects model

表7 非线性混合效应模型评价Table 7 Test of nonlinear mixed effects model

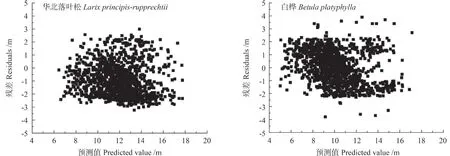
图1 不同树种的残差分布Fig.1 The residual distribution of different species

4 结论与讨论

本研究以方法研究为主，确定Richards 为构建华北落叶松与白桦针阔混交林基础模型，随着林龄的增加，树高与胸径关系受多种林分因子影响，通过Pearson 相关性分析确定了海拔、林分总断面积是影响华北落叶松与白桦混交林树高与胸径关系的主要因子；基于参数主要影响因子及最优基础模型，构建了包含哑变量的树高与胸径关系混合效应预测模型，当随机效应作用在林分断面积上时，包含哑变量的树高与胸径非线性混合效应模型具有更高的预测精度。

为了研究针阔混交林中多树种树高与胸径关系预测模型，本研究基于5 种具有生物学意义的基础模型进行拟合与评价，结果表明Richards 模型拟合精度最高，并与部分学者研究结果相同[29,34-36]。然而，有学者[10,37]认为树木生长会受到林分特征、树木竞争关系、立地条件及经营管理水平等[29,31]多种因素制约，Marziliano[17]研究表明林龄和密度是影响树高与胸径关系模型主要因子，并构建了包含林龄和密度的树高与胸径关系预测模型；而Crecente-Campo 等学者[38-40]则用含有优势木胸径、优势高以及林分密度等变量的树高与胸径关系模型来描述树木树高与胸径的关系。本研究通过相关性分析确定林分断面积和海拔是影响针阔混交林树高与胸径关系模型的主要因子，构建了包含林分断面积和海拔因子的树高与胸径关系模型，其中海拔会影响温度从而进一步对树高和胸径生长产生影响[1,7,36]，而林分断面积在一定程度上反映了林分结构对树木树高和胸径生长产生影响[28,30]。

本研究将林分断面积和海拔作为组合变量，构建了包含哑变量的多树种树高与胸径关系混合效应模型。基于哑变量构建的预测模型其拟合精度高于分树种构建的预测模型[20]，包含随机效应的预测模型精度高于未包含随机效应预测模型，其他部分学者[30-42]通过研究不同林分类型树高与胸径关系模型，均表明混合效应模型在拟合精度和预测精度上均高于基础模型，Huang 等[40]认为随机效应能够有效解决样地及单木水平间差异性。树木在生长过程中，不同林分类型其树高与胸径关系会受到多种因子影响，有学者[27,35-38]基于林分密度、优势高、林分断面积及空间位置等影响变量，构建了不同变量或变量组合的非线性混合效应模型，均在不同程度上提高了模型预测精度。当随机效应参数作用于林分断面积时的预测精度高于随机效应参数作用于海拔，当构建林分断面积和海拔两水平非线性混合效应模型时，不同模型采用了同一参数初始值和收敛准则，导致模型参数不收敛。在今后构建多树种的树高与胸径关系模型研究中，多水平非线性混合效应建模技术与方法还需进一步深入研究和探讨。