LTE高铁环境下OFDM载波间干扰消除优化研究

徐 岩， 丁 峰

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

高速铁路场景下的无线通信与传统的陆地移动通信相比有着显著的区别[1-2]，高速运行列车所引起的多普勒平移与快衰落使通信信道成为非恒定时变信道，以致产生载波间干扰，最终导致产生通信信道内的载波间干扰ICI(Inter-Carrier Interference)，这会对信号传输的误码率[3]性能产生影响，严重破坏了高速铁路的无线通信环境。

目前国内外对ICI载波间干扰的主要解决方法有均衡算法和自消除算法，文献[4]采用最小均方误差均衡算法，但该算法当载波数较大时，因其计算复杂度较高难以完全实现；文献[5]采用并行干扰消除算法，通过对子载波进行粗均衡后消除干扰矩阵中的非对角线元素，此法运算速度较快，但在高速场景下其接入信道为双选择性信道，粗均衡误差较大，准确度难以提高。对于干扰自消除技术，其核心是通过对发射信号和接收信号进行处理，使其每个接收信号上的ICI能够从内部相互抵消[6]，此类方法的优点是采用了差分调制，因此不需要对信道进行估计，但载波利用率仅为50%。文献[7]在此基础上提出相位旋转共扼消除算法，算法在时不变信道中能达到较好的ICI消除效果，但对于高速移动场景下所产生的时变信道却很难达到预期的效果。

本文提出一种重新排列发射端数据结构改变子载波序列的映射方式，将循环前缀CP(Cyclic Prefix)序列与各子序列最优函数加权相结合，这能有效抑制接收到的符号干扰，消弱LTE通信系统中由子载波频偏所引发的不良影响。

1 系统模型

本文以京张高速客专为例进行分析，通过图1测量的多场景下的信道概率密度函数PDF(Probability Density Functionn)，可以得出接近90%的信道冲击响应为单径、2径和多径的总概率只占10%左右，列车主要运行的场景为丘陵和平原高架，其多径特征相似，信道冲激响应以单径为主。

图1 京张铁路不同场景下的多径数量

高铁LTE采用双通道远端射频单元RRU (Radio Remote Unit)技术进行覆盖组网[8]，完全区别于传统低速通信场景下服从瑞利衰落分布的Jakes信道模型[9]，因此需要对现有的陆地通信结论加以改进。本文针对高铁信道模型进行建模，在实际运营环境中，郊区丘陵等地区基站和高速列车间的大型建筑物较为稀少，以直射径为主，从而存在一条较强的直射径与若干条非直射经。综合以上因素并结合考虑铁路沿线通信基站对信道的多径时延的影响，可采用莱斯衰落信道模型来模拟高铁信道，为简化其算法的复杂度，本文提出了一种线性模型，将信号接收到的到达角AOA(Angle of Arrival)均匀分布，并将散射信号相同分布，最终通过一阶泰勒级数表达，其信道的冲激响应可以表示为

h(n)≈nh1+h0

( 1 )

式中:h0为OFDM同步的平均信道数;h1为时域信道所接收到的样本信号，且它们均为常系数。

一个由N个子载波构成的模拟OFDM系统，若系统的总带宽为B，被分解成N个带宽相同的子通道，子通道间的频率间隔为

( 2 )

频域信号通过逆快速傅里叶变换IFFT表示为

0≤N≤N-1

( 3 )

式中:X(k)为OFDM输出的频域信号。为消除载波间干扰，需在各有效的OFDM符号前插入一个循环前缀CP信号，即在x(n)前插入保护时间间隔长度为Lg的循环前缀，从而生成等效传输信号。基带传输的OFDM信号的符号x(n)长度为N+Lg,可表示为

x(n)=x(n+N-Lg) 0≤n≤Lg+N-1

( 4 )

当接收信号历经频率选择性多径衰落后，则接收到的信号可以表示为

( 5 )

式中:h(n)为信道的冲激响应;w(n)为时域加性高斯白噪声。所接收到的时域信号y(n)可以通过快速傅里叶变换得到其频域表达式为

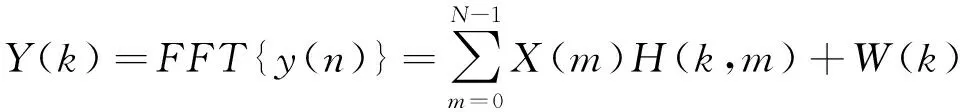
k∈[0,N-1]

( 6 )

式中:W(k)为信道加性噪声的快速傅里叶变化。

由于列车高速移动所导致的多普勒平移致使信道变成非恒定的时变信道，可分为受干扰部分的信道冲激响应式( 7 )和未受干扰下的冲击响应式( 8 )两种情况分别进行讨论。

( 7 )

(8)

式中:H(k,m)为第k个子载波与第m信道的冲激响应。高速环境下LTE的OFDM系统在一个符号的持续时间内与多普勒频率相比，子载波间隔较大，此时的信道变化充分满足线性近似，可将信道的冲激响应用线性模型来替代，将OFDM符号周期内的每一个时变信道路径用h(n)进行近似实现[10]。因此ε(k,k)和ε(k,m)分别表示为

( 9 )

(10)

代入原公式并化简可得频域信号Y(k)。

k=0,1,…,N-1

(11)

从式(11)中可以看出，接收端所接收到的频域信号Y(k)不仅包含每个载波原有发送的期望信号，还包括了式(11)中的第2项，为其他载波对当前载波的ICI干扰部分。假设信号处于传统低速通信场景瑞利衰落分布的Jakes信道模型[11]，OFDM符号将在一个信道的传输过程中不会随时间而发生改变，即每个复杂路径增益是一个时不变系统，故此时的H(k,m)=0。式(11)中的ICI干扰部分为零，此时可以判断ICI干扰项将不复存在， FFT只解调第k个子载波上的调制数据信号。然而，这种假设并不适用于高速移动列车通信条件下的时变通信系统，尤其对高多普勒引起的时变性所产生的子载波间干扰ICI有巨大影响。若不通过补偿等手段达到减小或者消除， ICI干扰项部分将得不到消除。

2 基于ICI的自消除和函数线性加权联合算法

由以上可知Lg为CP的循环前缀，并进一步假设CP循环前缀的长度比最大传播延时L-1长，因此CP循环前缀中将会出现部分未受到ICI[12]的干扰部分，如图2所示，其长度可表述为

q=Lg-L+1

(12)

图2 接收端抽取的时域信号子序列

接收端所接收到的信号，按OFDM序列的长度，可以划分为q+1个时域子序列，分别用y0,y1,…，yq来表示[13-14]，其子序列可以表示为

k=0,1,…,N-1

(13)

对时域序列进行N点的FFT变换，可以得到频域子序列Yd(k)为

X(k)ej2πm(n-d-l)/ne-j2πkn/Nej2πdk/N+

(14)

通过利用接收端所接收的每一个符号序列，对式(14)中未被干扰的序列抽取其子序列，并通过对接收的频域子序列设计合适的权值，使其能够有效减小ICI，最终得到一个使ICI减小且长度保持不变的OFDM符号序列Z(k)，可用于接收的期望信号项、ICI干扰项和高斯白噪声干扰项表示为

k=0,1,…,N-1

(15)

式中：

(16)

(17)

(18)

图3 子序列加权流程

(19)

(20)

(21)

(22)

且满足

(23)

这种权值的分配设置可将其接收到干扰部分少的子序列分配更大的权重值，使受到干扰严重的子序列分得更少的权重值，在相对于线性平均加权计算复杂度没有增加的前提下，性能却得到了大幅度提升，通过这种合理配置方案能有效地抑制ICI干扰。

图4 一次函数线性权值分配

3 试验仿真与分析

采用线性信道模型对时变信道进行仿真时，可通过SIR接收机输入端接收信号质量和BER指标对系统传输的可靠性进行评估，然后比较优化后的BER的量值，分析ICI性能与系统性能间的期望值变化，仿真参数如表1所示[16]。

表1 系统仿真参数

图5为在速度为350 km/h条件下分别对加权联合算法、自消除算法及原始标准算法进行SIR仿真分析及比较，可以看出在相同归一化多普勒频率的条件下，ICI自消除和一次函数线性加权联合算法，比使用自消除算法在性能上得到了进一步的提升。联合算法甚至比原始算法下的SIR性能至少提高10 dB以上，有效改善了系统的通信性能。究其主要原因是在没有其他衰减的情况下，接收的所有信息都被解码到了规定的信号中。这种ICI消除模式对于OFDM的影响是显著的，它保证了能量在整个SIR范围内不会快速下降。

图5 联合算法对SIR的改善(350 km/h)

从图6可以看出，采用基于ICI自消除和一次函数线性加权联合算法的BER性能，几乎能达到与莱斯信道模型理论值相接近的效果。但将系统应用于时变信道时，信道存在较为严重的多普勒频移扩展，从仿真图图7中可以看出，本文所提出的联合算法能明显降低误码率，从而说明该方法对时变和非时变信道均能够适应。

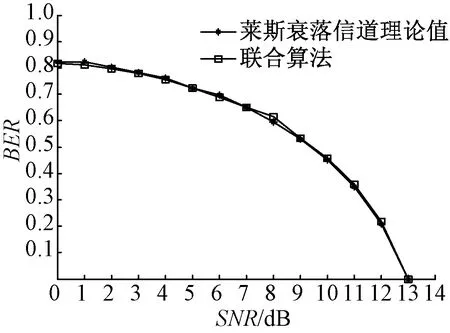
图6 莱斯衰落非时变信道模型的BER性能

图7 时变信道模型的BER性能

为了验证该方法是否能在不同的速度区间均能达到预期的效果，图8仿真了在100～400 km/h速度区间段的误码率性能，可看出本文所提出的联合算法的BER指标均明显低于OFDM系统和自消除算法对应的BER，再次验证了本联合算法在各个速度范围内均能有效地降低BER。

图8 BER随列车速度变化曲线

4 结束语

本文从载波间干扰ICI与LTE系统BER性能的角度进行分析比较，讨论了ICI对OFDM的影响。针对超高速移动场景下的非平稳时变信道LTE系统的ICI消除问题，本文在降低计算复杂度的线性模型的基础上提出了一种ICI自消除一次函数线性加权联合算法，仿真实验表明，该自消除联合算法不仅能有效减小ICI干扰，提高系统的SIR，在时变及非时变信道中均表现良好，也能在不同速度区间内有效降低通信误码率，提高车辆高速运行时的通信质量。