航道长度对波浪传播影响试验研究

乔吉平，吴月勇，郝枫楠，赵 地，柏 杨

(1.黄河勘测规划设计研究院有限公司，河南 郑州 450003；2.河南省城市水资源环境工程技术研究中心，河南 郑州 450003)

船舶的大型化以及深水化是各国航运发展的趋势，也促使了进港航道、港池深水化。然而航道的开挖会对航道区域的波浪传播变形发生影响。国内外的众多学者近年来针对航道对波浪传播的影响做了大量的研究。其中，赵智邦等[1-5]结合物理模型试验取得了一定的成果：赵智邦[1]分析了入射波浪分别呈小角度发散、临界角度入射、大角度穿越3种方式入射航道区域对港域波能分布的影响；杨宪章等[2]通过几个港口工程模型试验实例，论述了航道对波浪的作用及航道走向对港内泊稳条件的影响；陈汉宝等[3]发现了航道边坡处发生的波高水深比大于1的情况并采用极限波高理论加以论述；刘青明[4]、林尚飞等[5]探讨了波浪入射角度对港内泊稳条件的影响，并对港区航道平面布置提出建议。此外，孙克俐等[6-15]采用波浪数值模型也取得了较多研究成果：孙克俐等[6]、李思源等[7]利用波浪数值模型提出了能够减少航道外的波能集聚的航道开挖方案；刘爱珍[8]、柳淑学[9]分别利用改进的Boussinesq方程并依托理想地形，分析了波浪入射角对防波堤口门处航道及港内波高的影响；徐俊锋等[10]、冯明威[11]、郭科[12]利用MIKE21 BW模型，系统地分析了航道尺度和波浪条件对波浪传播变形的影响；张娜等[13]研究了波浪以临界入射角情况下的波浪数学模型中的航道长度选取问题；李玉成等[14]通过缓坡模型，尝试采用在航道周围局部开挖的方式来改善由于航道折射所导致的防波堤区域波高异常增大的情况；左其华等[15]以大亚湾的一典型航槽为例，分析了航道断面的波高分布规律与波浪入射角之间的关系。

前人在开展上述物理模型、数值模型试验时，要么由于试验场地限制、造波机尺寸不足、兼顾计算效率与精度的原因，常常采用截短航道的做法来进行局部地形模拟；要么并未详细考虑航道长度对港域波浪传播的影响，只是把重点放在波浪条件以及航道尺度(宽度、深度、边坡)对港域波浪传播的影响。鉴于此，本文以MIKE21数值模型试验为主，物理模型试验为辅，研究了不同波浪条件(波高、周期、波浪入射角)下，港域波高随航道长度变化的关系，并针对不同区域给出航道长度取值建议。研究成果对后续航道工程物理模型、数值模型试验的开展以及港口航道工程规划有重要参考价值。

1 模型验证

1.1 波浪物理模型

物理模型试验主要针对揭阳港南海作业区2号港池的公共航道工程和防波堤工程建立物理模型，试验遵循重力相似律并按《波浪模型试验规程》的有关规定进行模拟，模型的几何比尺为1∶55。试验采用断面板法模拟地形，模型几何误差、地形高程误差均控制在±2.0 mm以内。港池边界布置有上下3层人造消浪栅，能够较好地减少港池边界的反射作用。试验在浙江大学海洋学院的40 m×70 m×1.8 m波浪港池中进行，造波机尺寸为34 m×56 m。试验波浪采用单向不规则波，波浪谱为标准JONSWAP谱，每组不规则波采集3次，采集时间保证具有180个以上的波浪被采集到，最后取3次结果的平均值作为最终结果。此外，波面数据采用LG1型电容式浪高水位传感器采集，测量精度可达0.3 mm，模型共布置29个浪高仪，模型布置见图1。

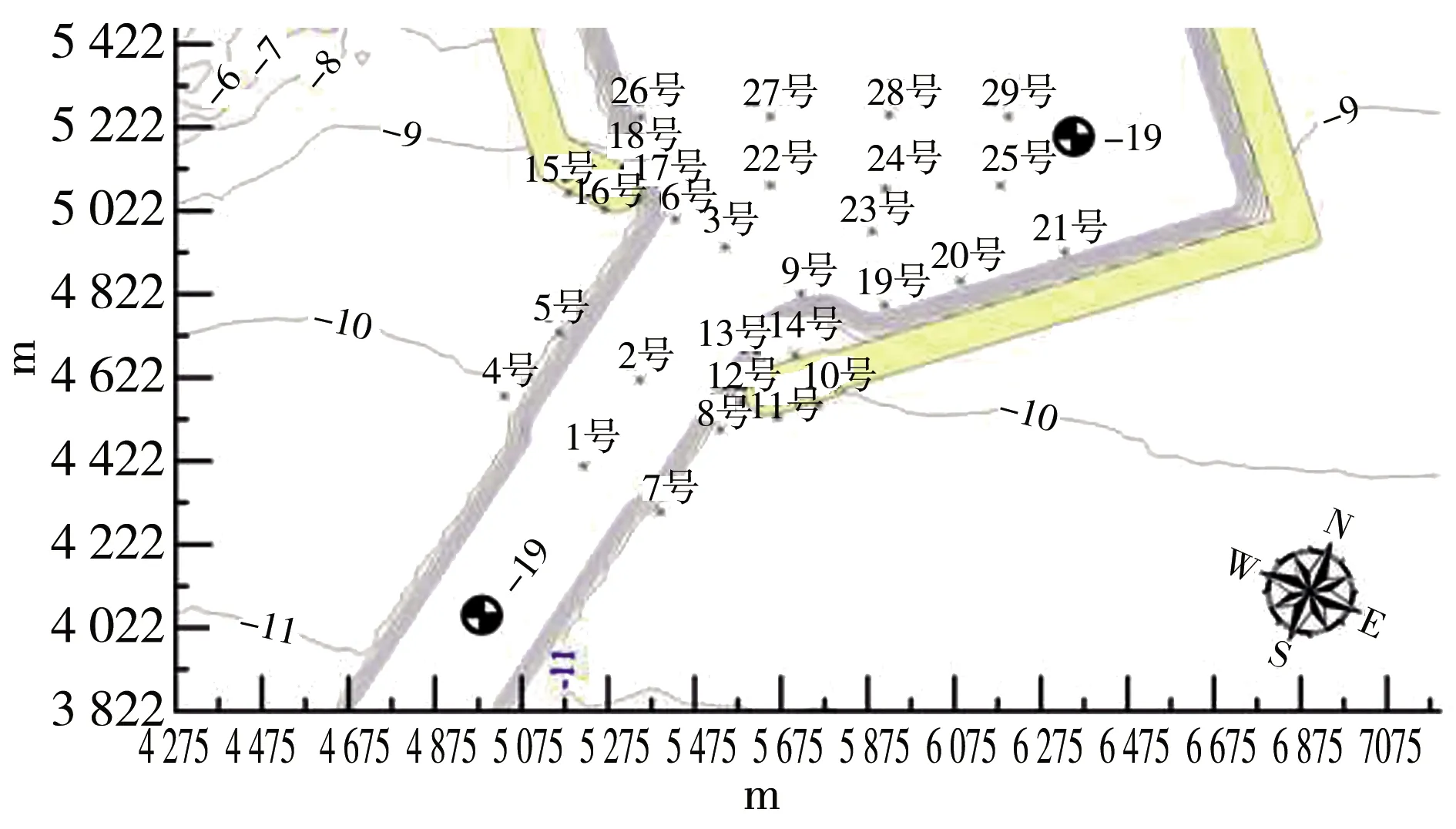
图1 模型布置

试验时以1号特征点作为控制点，试验波浪工况按表1进行组合，S、SSE和SE向波浪与主航道轴线所成的入射角θ(波向与航道轴线的夹角，按航道轴线逆时针起算)分别为10.5°、33.0°、55.5°。各特征点的平面布置暨物理模型平面布置见图1。试验工程区域海底地形模拟至-11 m附近，地形末端采用1∶10的坡度过渡到港池底部(港池底高程-19 m)，模拟航道长度l为1 580 m。

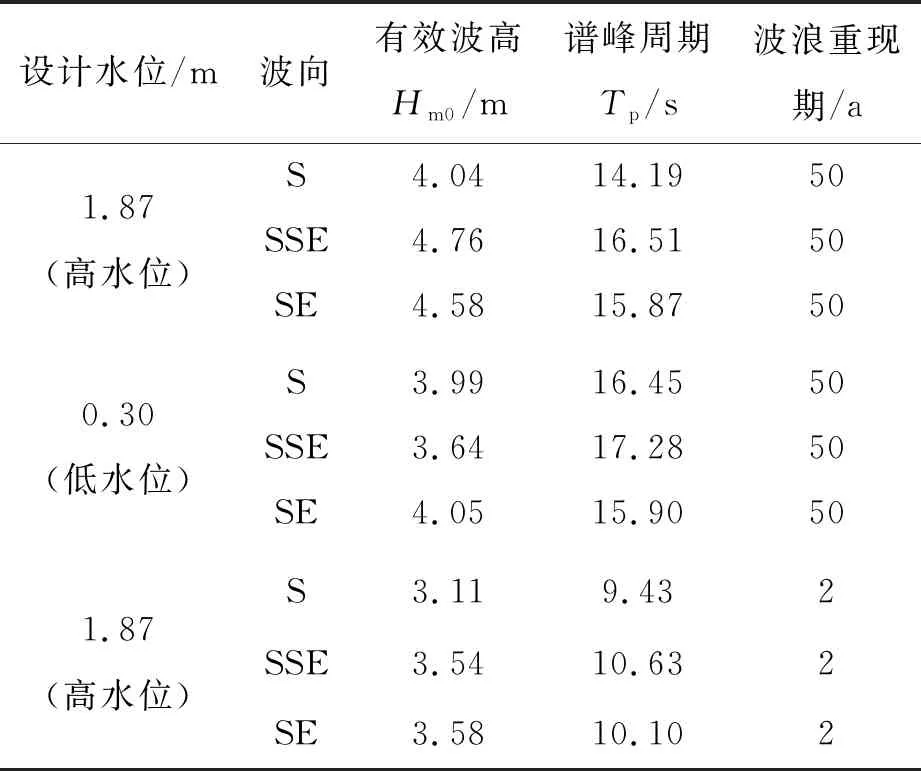
表1 特征点设计波浪要素

1.2 波浪数值模型

数值模型计算软件采用国际上公认的MIKE21软件，具体为基于Boussinesq方程的BW模块，MIKE21 BW模块能模拟缓变地形或复杂变化边界条件下的波浪传播变形。MIKE21 BW模型中采用内部内部造波源函数法进行造波，造波线设置在模型底端处深水区域，波浪由深水向浅水传播，并在造波线后方设置海绵层以达到吸收反向传播波能的目的，海绵层厚度取为20层，总厚度为120 m，见图2。

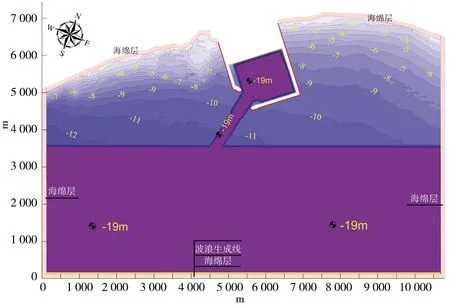
图2 MIKE21 BW数值模型设置

模型计算采用正方形网格，空间步长取为6 m，时间步长取为0.08 s；每组试验模拟时间为50 min，保证统计分析的波个数在250个以上。在港池内部及港外防波堤身、堤头处设置孔隙层以模拟建筑物的反射系数，港池外部边界区域的反射系数取为0.25～0.40，模拟扭王字护面块体的反射；港池内边界东、南、西侧反射系数取为0.99，模拟直立式结构全反射；港池内边界北侧反射系数取为0.15～0.30，模拟物理模型中的港池边界弱反射的斜坡式消浪网结构。

波浪数值模型的模拟区域范围约为10 800 m×7 440 m，航道开挖后的地形见图2。为了更好地与物理模型相验证，在数模验证时将地形、航道的模拟范围与物理模型相同，在模拟地形末端同样采用1∶10的坡度过渡到模型底部平底区域。数值模型计算的波浪类型为单向不规则波，波谱参数均与物理模型中的波谱参数相同，波浪输入条件完全与表1相同。

1.3 验证结果

通过对比分析数值模型、物理模型的试验结果发现，各波向、各重现期下的物理模型、数值模型在各测点的波高大小吻合良好。绝大部分工况的最大相对误差都在50%以下，且最大相对误差较大的工况都出现在小波高测点处，这些测点波高的绝对误差值并不明显。同样地，绝大部分工况的平均相对误差都在±10%以内，只有2组工况的平均相对误差达到了-43.30%和-40.98%，但这是由于物理模型的强非线性作用所致。图3—5列出了典型的数值模型、物理模型波高验证对比，三图说明除了波高大小外，各测点的波高分布规律也较为吻合，数值模型验证效果较好。

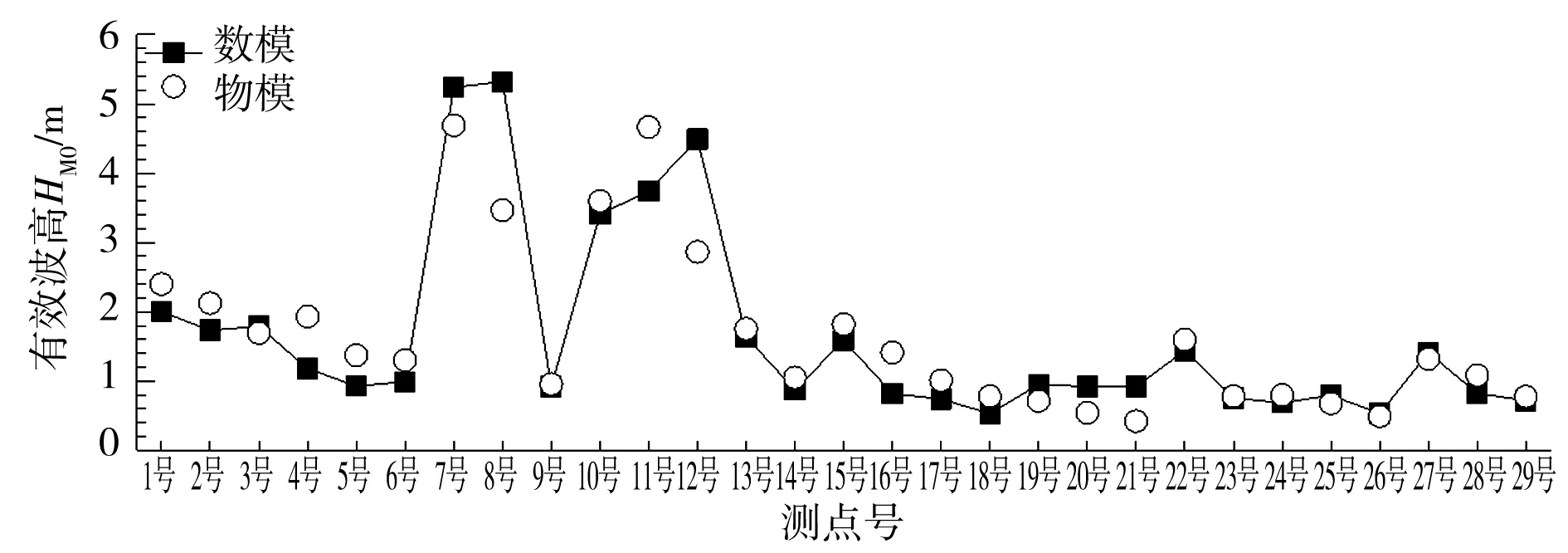
图3 S向，设计高水位，2年一遇波浪

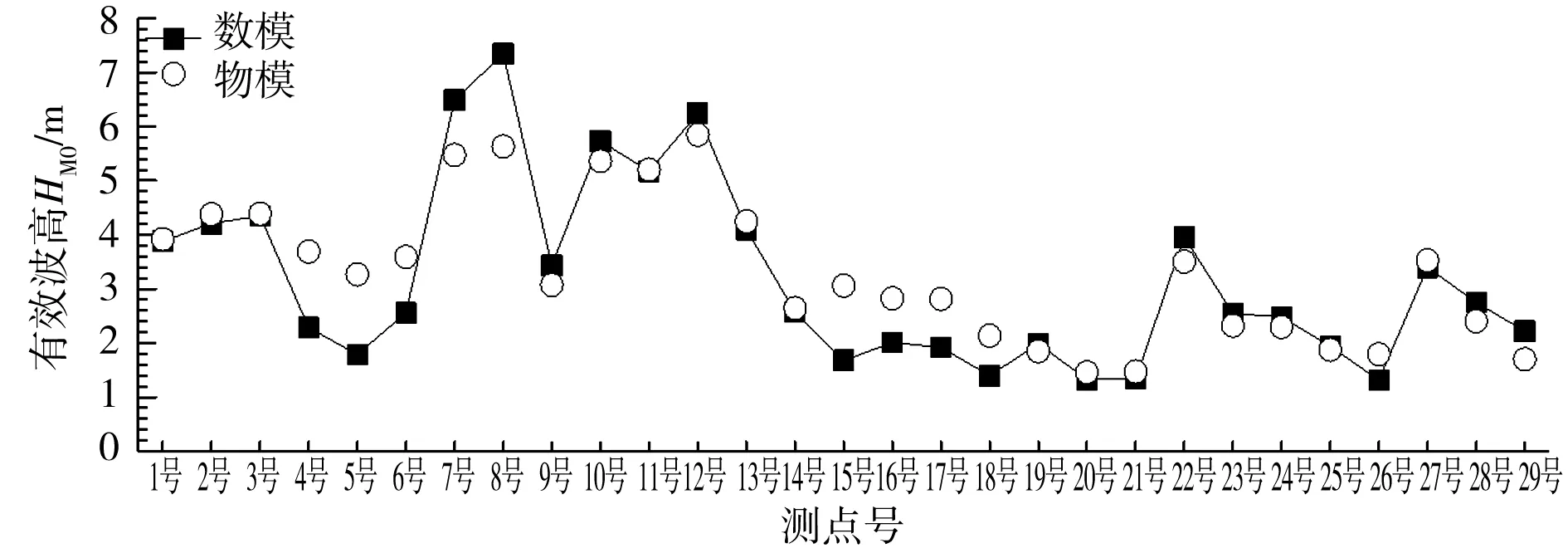
图4 SSE向，设计高水位，50年一遇波浪

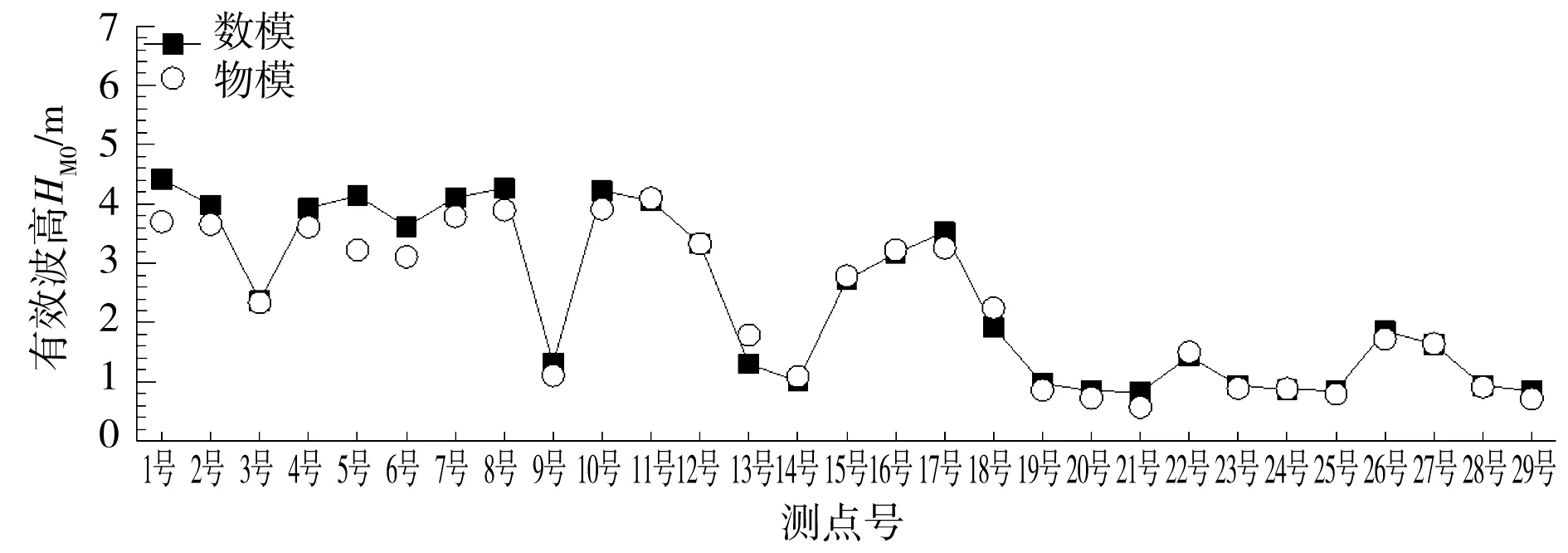
图5 SE向，设计低水位，50年一遇波浪

2 航道长度对港域波浪的影响

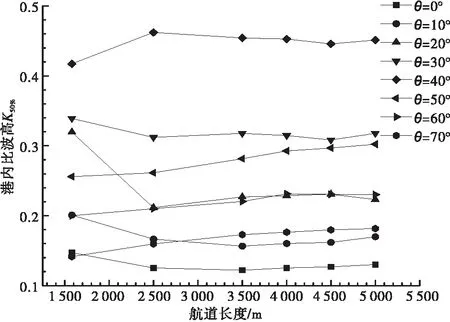
在数值模型验证较好的基础上，为了更方便、经济地分析航道长度对港域波浪的影响，继续采用BW数值模型进行后续模拟分析。数模采用的航道长度及波浪条件组次包括：航道长度l分别为1 580、2 500、3 500、4 000、4 500、5 000 m；有效波高Hm0分别为1、2、3 m；谱峰周期Tp分别为6、9、12、15、18 s；波浪入射角θ分别为0°、10°、20°、30°、40°、50°、60°、70°。试验组次采用控制变量法来进行，保持航道宽度B=240 m、航道边坡γ=1∶7、航道内水深h=20.87 m固定不变，波浪条件采用全交叉法来进行组合，试验组次共计96组。

为了分析不同波浪条件下航道长度对港域波浪的影响，将港域分为三类，分别为港池内、航道迎浪侧、航道背浪侧。引入港内比波高的特征大值Kmax、K50%这两个概念，分别表示港内所有位置比波高最大值、港内所有位置的比波高中位值。由于港内泊稳条件由大波高来控制，用这两个特征值的变化情况基本可以反映航道长度的改变对港内波高值大小及其分布的影响情况。图6中的斜线阴影区域为港内比波高特征值的统计范围。

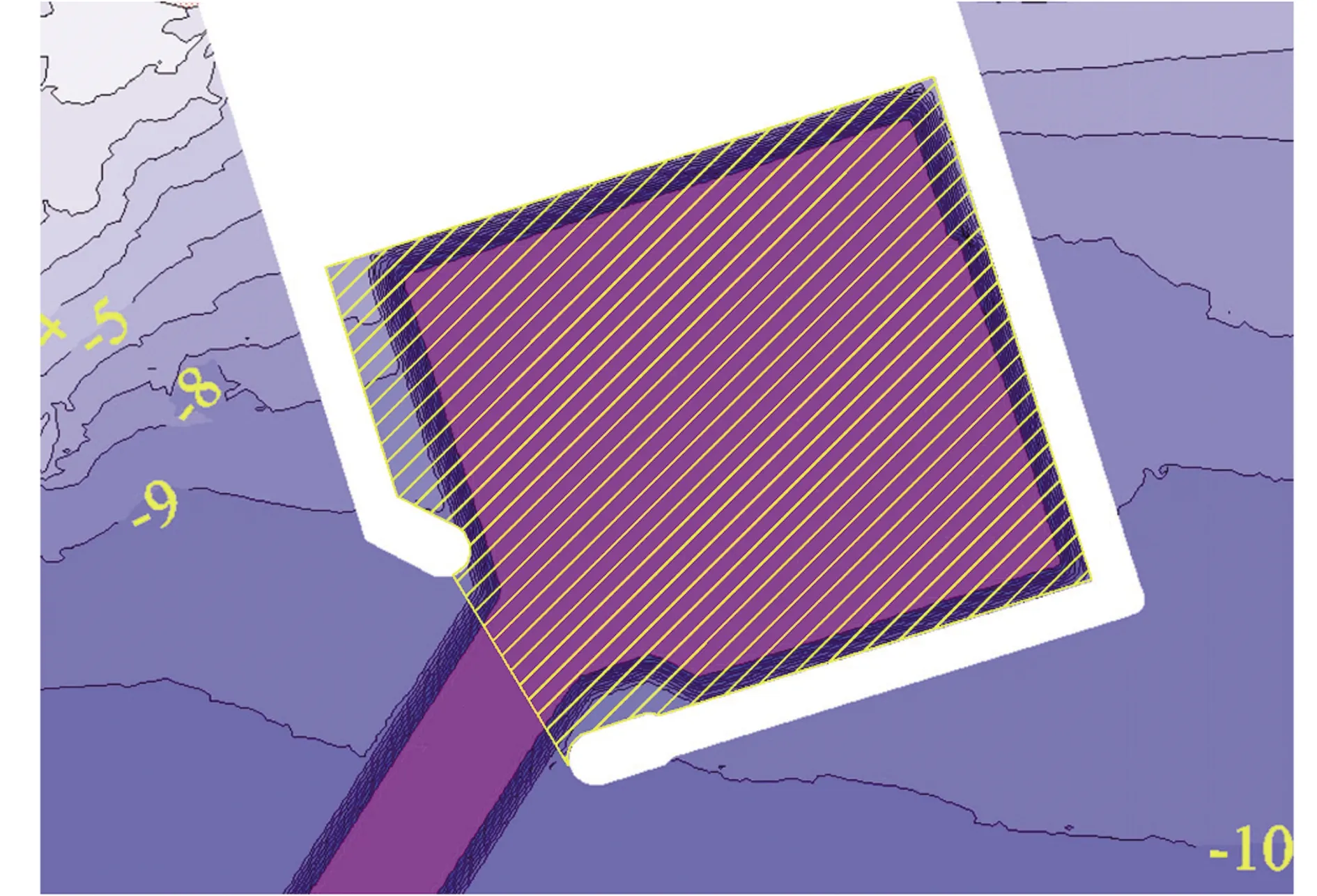
图6 港池内比波高统计范围示意

2.1 波高的影响

不同入射波高波高的工况下，波浪经由航道地形作用后传播至港池内的港内比波高Kmax、K50%值随不同航道长度l的变化规律见图7。由图7可知，港内比波高Kmax、K50%值随航道长度的变化规律都是先减小再保持稳定，临界航道长度lC约为3 500 m，此后航道长度的增加对港内比波高特征大值基本不再有影响。此外，图7中各波高代表的3条曲线彼此之间偏差很小，这说明波高大小对港内比波高特征大值的影响很小。此外，计算结果显示：各波高工况下的迎浪侧、背浪侧比波高在不同航道长度下的分布也基本相同，即波高变化对航道长度的选取并无明显影响。

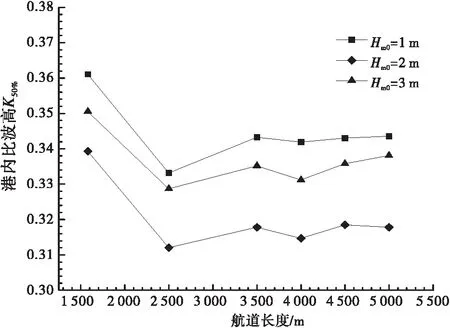
b)K50%

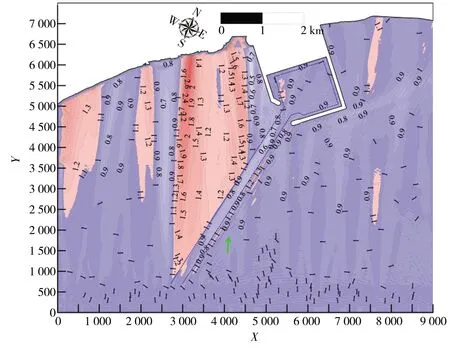
试验中发现航道长度的变化对港域不同位置处的波高影响不同，图8给出了Hm0=2 m、Tp=15 s、θ=30°的典型工况下，港域两组航道长度(短航道比上长航道)之间的波高比值分布。由图8可知：当航道长度较短时(l=1 580 m)，由于航道折射作用的差异，港内波高明显大于长航道工况，且当航道长度l达到3 500 m后，港内的波高分布基本不再发生改变，可认为航道临界长度lC=3 500 m。图8再次说明了用港内比波高特征大值的变化情况来判断航道长度对港内波高影响是正确的。

此外，通过比较图8对应工况下多组航道长度之间的波高比值分布还发现：航道长度对迎浪侧的波高分布的影响是有限度的，航道继续加长到4 000、4 500 m之后，航道折射对迎浪的波高影响有限，迎浪侧的波高比值都在0.95～1.00之间，可认为航道迎浪侧的临界航道长度lC为4 000 m。对背浪侧的波浪而言，短航道折射的波能集中带的位置更靠近港池，故当工程区域布置在航道背浪侧，则航道长度不可过短，应至少使航道背浪侧的波能集聚区域不受建筑物的反射影响；航道背浪侧存在一个有效区域，在该区域内，用截短航道的方法模拟效果近似可与长航道工况等同。当波浪入射角θ=30°时，航道背浪侧区域的有效区域为从航道末端开始，波浪入射波向与航道轴线所夹区域(自航道轴线逆时针起算)。

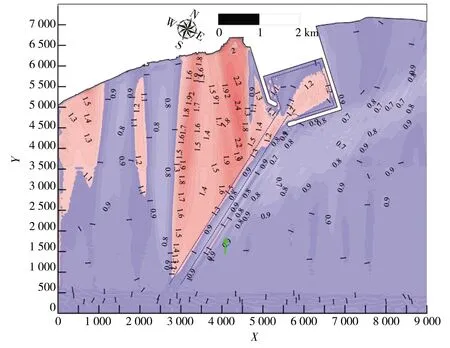
a)1 580 m长航道比5 000 m航道

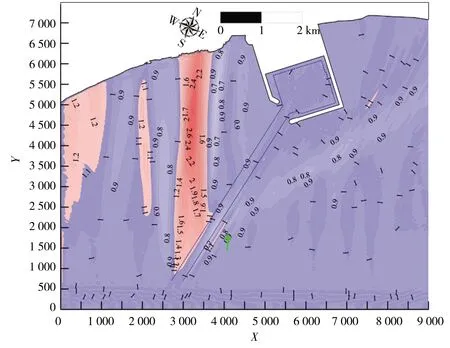
b)3 500 m长航道比5 000 m航道

2.2 周期的影响

不同入射周期T工况下，波浪经由航道地形作用后传播至港池内的港内比波高Kmax、K50%值随不同航道长度l的变化规律见图9。由图9可知，随着波浪周期的改变，港内波高的临界航道长度lC的数值均为3 500 m，这与图7所反映的结论相同。

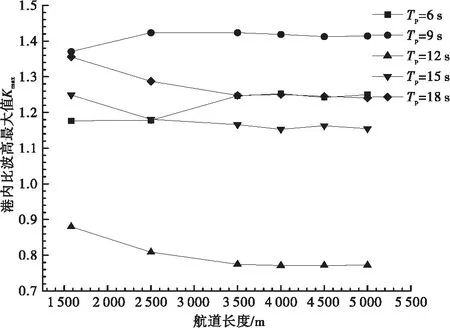
a)Kmax

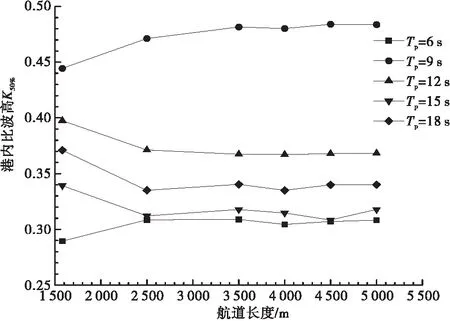
b)K50%

此外，周期的改变对临界航道长度的选取有较大影响，图10给出了Hm0=2 m、Tp=9 s、θ=30°的典型工况下，港域两组航道长度(短航道比上长航道)之间的波高比值分布。受航道折射作用的不同，导致不同周期下的港域波高分布存在差异，图8、10可分别代表长、短周期下的港内波高比值分布的变化特征。经过多种周期、航道长度组合模拟结果显示：当Tp=6～18 s时，迎浪侧的临界航道长度lC为4 000 m，该航道长度下迎浪侧的波高模拟效果可与长航道工况等同，港池内波高对应的临界航道长度lC固定为3 500 m；当Tp=12～18 s时，航道背浪侧的模型有效区域为从航道末端开始，波浪入射波向与航道轴线所夹区域(自航道轴线逆时针起算)；当Tp=6～9 s时，短航道背浪侧不存在模型的有效区域，在截短航道时需要慎重。

a)1 580 m长航道比5 000 m航道

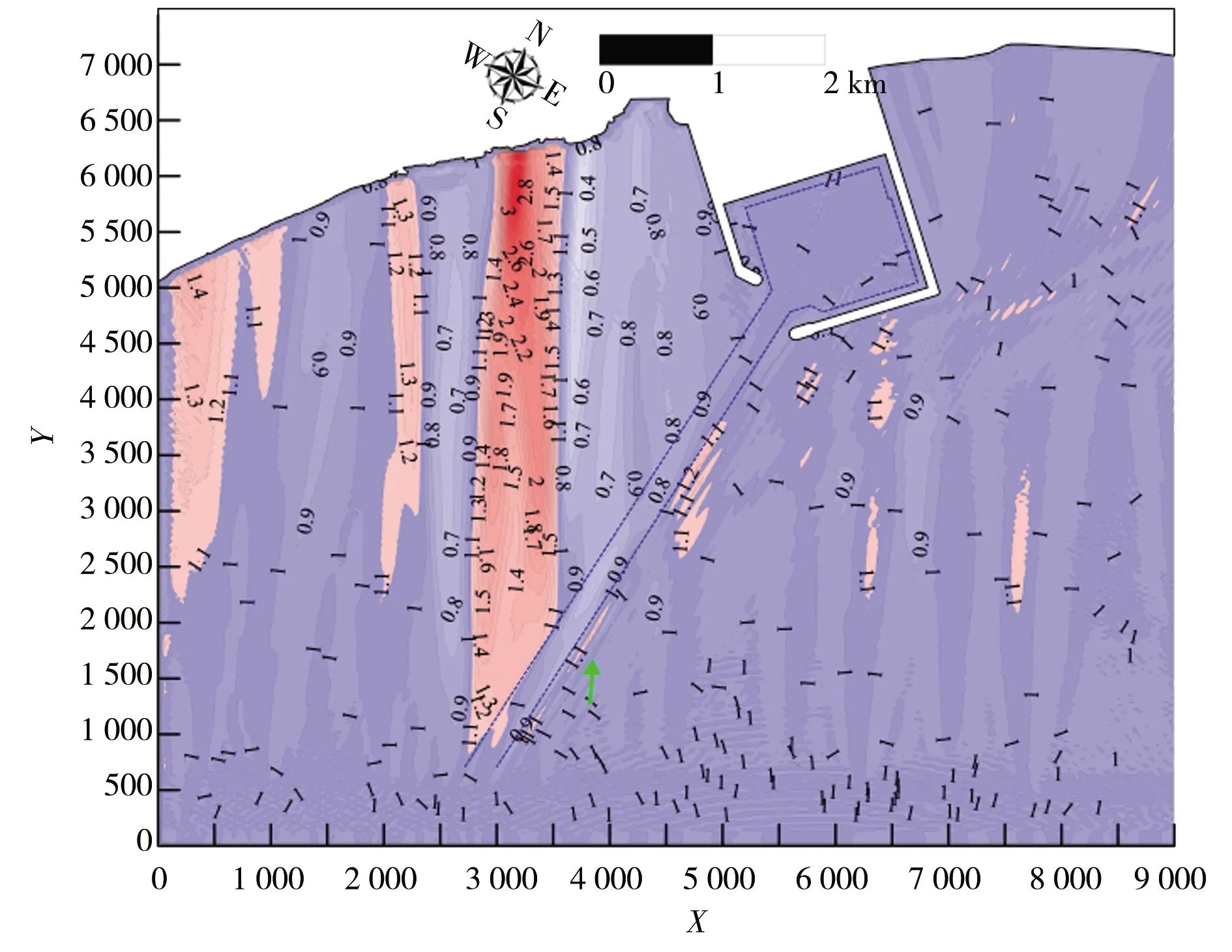
b)3 500 m长航道比5 000 m航道

2.3 波浪入射角的影响

不同波浪入射角θ工况下，港内比波高Kmax、K50%值随不同航道长度的变化规律见图11，由图11可知随着θ的改变，港内波高对应的临界航道长度lC均为3 500 m。

同样的，θ对航道长度的选取有较大影响，图12、13分别给出了θ=10°、60°两种典型工况下，港域不同航道长度的波高比值分布，其可以分别代表波浪小角度入射航道和大角度入射航道下的航道长度对港域波高分布的影响，与图8中的θ=30°工况共同展现了不同范围入射角对航道长度选取的影响。经过多种波浪入射角、航道长度组合模拟结果显示：①当θ介于40～70°，航道长度的改变对迎浪侧区域的波高分布影响很小；②当θ介于0～30°，迎浪侧对应的临界航道长度lC=4 000 m，l大于4 000 m后仅对航道末端附近的波高分布有影响；③当θ介于30～70°，航道背浪侧的有效区域为从航道末端开始，波浪入射波向与航道轴线所夹的锐角区域，在该区域内，用截短航道的方法模拟效果近似可以与长航道工况等同；④当θ介于0～20°，短航道工况下的的背浪侧波高明显大于长航道工况，在物理模型或者数值模型中截短航道时则需要慎重；⑤当θ介于0～70°，对港池内的波高分布而言，航道临界长度lC=3 500 m并保持不变。

b)K50%

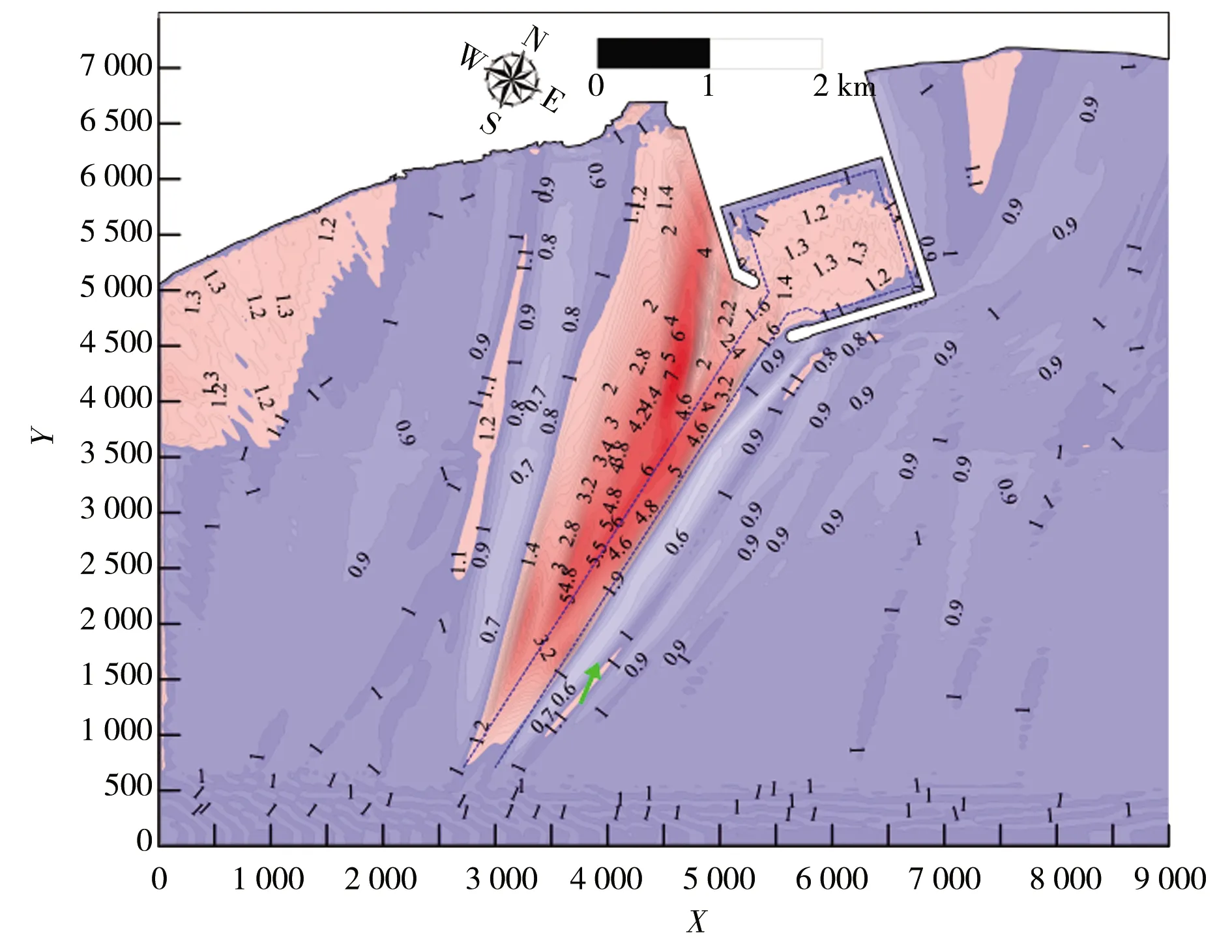
a)1 580 m长航道比5 000 m航道

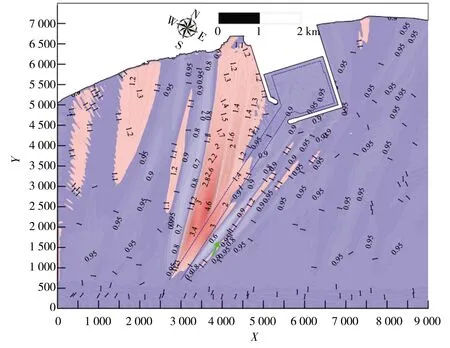
b)3 500 m长航道比5 000 m航道

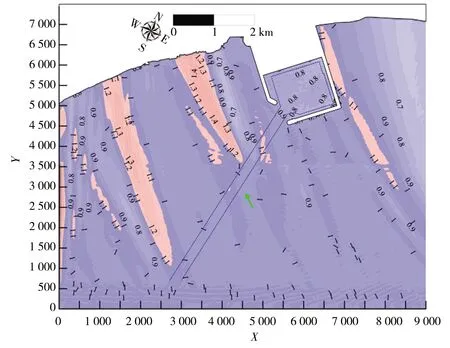
a)1 580 m长航道比5 000 m航道

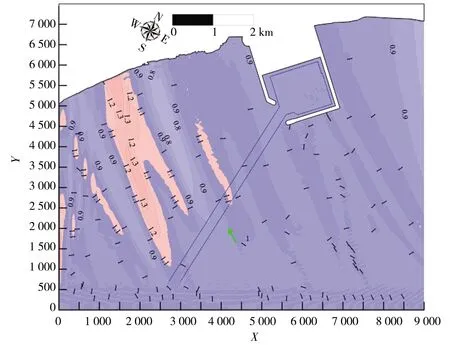
b)3 500 m长航道比5 000 m航道

3 结论

a)波高对航道长度的选取基本没有影响，周期及波浪入射角对航道长度的选取影响较大。

b)港池内波高对应的临界航道长度lC为3 500 m，不随波高、周期、波向的改变而明显变化。

c)波浪小角度入射时(0～30°)，迎浪侧的临界航道长度lC为4 000 m，该航道长度下迎浪侧的波高模拟效果可与长航道工况基本等同；波浪大角度入射时(40～70°)，航道长度的改变对迎浪侧的波高分布影响很小。

d)长周期(12～18 s)和波浪大角度入射(30～70°)时，航道背浪侧的有效区域为从航道末端开始，波浪入射波向与航道轴线所夹区域(自航道轴线逆时针起算)；短周期(6～9 s)或者波浪小角度(0～20°)入射时，短航道背浪侧不存在模型的有效区域和临界航道长度，在截短航道时需要慎重。