基于粒子群优化算法的舰机多设备组合搜潜决策方法
郁红波,张 驰,杨少伟
(1. 海军航空大学,山东 烟台 264001;2. 中国人民解放军92810部队,海南 三亚 572000; 3. 中国人民解放军91388部队,广东 湛江 524000)
随着潜艇建造技术的发展,潜艇下潜深度不断增加,降噪技术越来越成熟,单基地设备搜潜已经无法满足现代复杂的搜潜任务,因此舰机多设备组合搜潜技术是海军反潜重要的发展方向。对于舰机多设备组合搜潜,在保证搜潜效能的同时,又要兼顾经济性和隐蔽性,因此选择最优的舰机设备组合搜潜方案势在必行[1-3]。
舰机多设备组合方案博弈分析与确定性方案相比,具有复杂性,分析目标具有不确定性等问题,不易获得评价指标的权重信息,因此难以用权重已知的决策方法对舰机多设备组合方案进行计算和决策。对于多方案指标权重未知的问题,国内外也已开展了很多研究工作。汪伦焰在文献[4]中提出根据联系数理论,通过公式计算出联系数之间的距离,然后引进了相对相离度矩阵和相对相离度的定义,最后通过将区间数转化为联系数进行多属性决策;郭子雪等在文献[5]提出了基于离差最大化解决属性权重未知的方法,基于区间直觉模糊加权平均算子给出了属性权重未知情况下属性信息为区间直觉模糊数的多属性决策方法;代文锋在文献[6]中为了解决属性权重未知的多属性决策问题,运用前景理论得出了各个指标的二元前景值,并且建立了决策矩阵,根据主客观权重,计算得到指标的综合权重,基于扩展Multimoora算法对方案进行排序,最后运用占优理论进行最终的方案排序。本文针对属性权重未知多属性决策问题,提出了一种基于粒子群算法的博弈理论,通过粒子群算法的不断优化,求出均衡策略剖面,可以让各个属性在博弈中均能获得较好的收益,使得分析结果能够全面地反映各个属性包含的信息。
1 建立方案决策模型
1.1 确定舰机多设备组合搜潜方案集及评价指标集
现代反潜过程中有很多搜潜设备,针对不同的战场情况和敌我态势,通常使用单一的搜潜设备或者将搜潜设备两两组合形成主被动联合搜潜。主要的搜潜设备为声呐浮标(F),吊放声呐(D),拖曳声呐(S)。根据实际作战要求,形成如下方案集:U=(u1,u2,u3,u4)。
其中,各方案表示如下:
u1={F}为反潜直升机单独使用声呐浮标系统对潜艇进行搜索;
u2={D}为反潜直升机单独使用吊放声呐对潜艇进行搜索;
u3={F,D}表示拖曳声呐与吊放联合使用,通过吊放声呐发射声波,拖曳声呐接收声波进行主被动联合搜潜;
u4={S,F}表示拖曳声呐与声呐浮标主被动联合搜潜,拖曳声呐主动发射声波,浮标被动接收声波形成多基地搜潜方案。
对于上述的方案集,需要建立指标集对上述方案进行评价。考虑舰艇和航空反潜装备的特点,本文将从以下4个方面进行评价,评价指标集如下:P=(p1,p2,p3,p4)。
式中,p1为对潜搜索能力;p2为隐蔽能力;p3为跟踪及定位能力;p4为经济性。
通过建立方案集U和指标集P,可以得出舰机多设备组合搜潜方案决策结构,如图1所示。

图1 舰机多设备组合搜潜方案决策结构
方案ui在指标集pj上的指标值为yij(i=1,2,3,4;j=1,2,3,4),由指标值确定的矩阵为决策矩阵,记为A(yij)m×n,将矩阵A(yij)m×n规范化为矩阵R(rij)m×n,矩阵R(rij)m×n中的值蕴含着方案在各个指标集pj上的优劣顺序。
为消除不同指标集之间不同的量纲单位带来的不可公度性,可按下述规则将决策矩阵A(yij)m×n转变为规范化矩阵R(rij)m×n[7]。
根据不同类型的指标值属性,可将指标值属性分为成本型、固定型、效益型、区间型指标集。假设有m个方案,n个指标。
1)效益型指标
(1)
式中,ymax为指标中的最大值;ymin为指标中的最小值。
2)成本型指标
(2)
式中,ymax为yij中的最大值;ymin为yij的最小值。
3)区间型指标
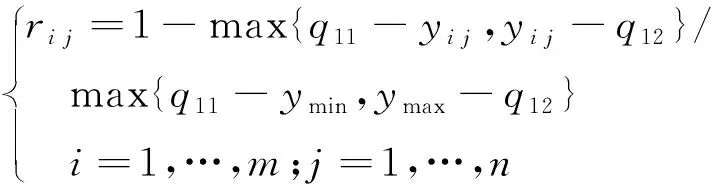
(3)
式中,ymax为yij的最大值;ymin为yij的最小值;q11、q12分别为区间的上下限。
4)固定型指标
(4)
式中,yj为目标属性的最佳稳定值。
1.2 符号的定义
1)优先序位v。假设有m种方案,对应的m个优先序位的集合记为v={v1,v2,…,vm}。根据优先序位,可以判断方案的优先顺序。在优先关系ui1>ui2>…>uim中,uik在方案序列中称为第k优先序位。在优先序位集合中,v1的优先级最高,vm的优先级最低。
2) 指标方案序p·v。对于一个特定的指标pj,方案集ui都有一个对应的指标值rij(i=1,2,…m)。根据yij确定的优先关系ui1>ui2>…>uim,称为指标pj的指标方案序。pj的指标方案序可以表示为pj·v。其中,pj·vk=xik表示指标pj确定的方案序中xik处在第k优先序位。

4)有效策略剖面。有效策略剖面σ={w1,w2,…,wn},并且满足约束条件[9-10]如下:
(5)
不符合约束条件的策略剖面称为无效策略剖面,因此,规定无效策略剖面的收益为0。
根据上述定义,舰机多设备组合搜潜博弈模型可以表示为〈I,S,H〉。其中,I表示各方案中的指标,即Ii=Yi;博弈策略S是对指标yi的权重wj进行赋值;H为博弈双方的收益矩阵,记为hj(σ),hj(σ)是决策方案序w·v和指标方案序p·v的相符度,记为Homo(w·v,pj·v)。
相同方案ui在序位v1和vm上对相符度的贡献不同。为体现相同方案在不同序位上对相符度的贡献,本文引入序位权,序位v={v1,v2,…,vm}对应的序位权为q={q1,q2,…,qm}。假设最低优先级序位vm对应的序位权为qm,则序位权的表达式为
(6)
序位权满足约束条件如下:
(7)
5)均衡策略剖面。舰机多设备方案博弈均衡时的策略剖面为σ*,由σ*产生的决策方案序σ*·v与任何指标方案序pj·v的相符度满足:
Homo(σ*·v,pj·v)≥Homo(σ·v,pj·v)
(8)
2 舰机多设备组合搜潜博弈分析算法及粒子群优化算法
2.1 博弈分析算法
舰机多设备组合搜潜博弈分析算法主要包括方案评估,求取决策矩阵,求解均衡策略剖面,利用相符度进行方案优选4个步骤。
1) 方案评估。分析舰机多设备组合搜潜方案的优缺点,获得方案对应的指标值;
2) 求取决策矩阵。根据每个方案的指标值求取决策矩阵A(yij)m×n,根据指标集的属性求取规范化矩阵R(rij)m×n,并根据R(rij)m×n,获得指标序pj·v;
3) 求解均衡策略剖面。利用粒子群优化算法,求出均衡策略剖面σ*=w*=(w1*,w2*,…,wj*);
4) 利用相符度进行方案优选。首先,使用均衡策略剖面σ*对规范矩阵R(rij)进行聚合,得出综合指标值,从而得出决策方案序ui1>ui2>…>uim;然后,计算由σ*得出的决策方案序σ*·v与指标序pj·v的相符度Homo(σ*·v,pj·v)。
综上所述,要想对舰机多设备组合搜潜方案进行决策分析,要求出均衡决策剖面σ*和相符度Homo(σ*·v,pj·v)。
2.1.1 求解相符度
1)方案ui和uj的相符度。
假设方案ui和uj在决策方案序w·v的序位分别为v1m和v2m。在指标方案序中,pj·v的序位为v1k和v2k,则在决策方案序中w·v1m=ui,w·v2m=uj,在指标序中pj·v1k=ui,pj·v2k=uj。若是在决策方案序w·v和指标序中pj·v均有ui>uj,则称决策方案序w·v和指标序pj·v关于方案ui和uj相符,其相符度定义为sub-homow·v,pj·v(ui,uj)=1,即博弈中收益为1,反之,决策方案集w·v和指标序中pj·v关于方案ui和uj不相符,sub-homow·v,pj·v(ui,uj)=0,即博弈中收益为0。
2)w·v和pj·v的相符度。
决策方案序w·v和指标序中pj·v之间的相符度定义为w·v和pj·v关于pj·v中每个方案与其他低优先级方案的相符度的加权和[8]:
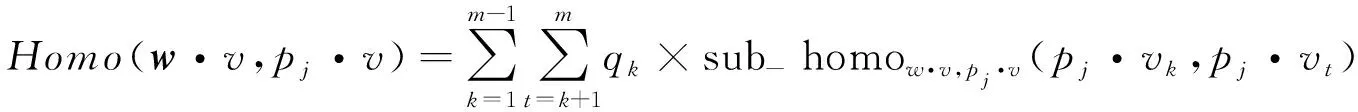
(9)
式中,qk为方案pj·vk的所在序位的序位权。
2.1.2 求解均衡策略剖面
w·v和pj·v之间的收益反映了决策方案序w体现指标pj包含信息量的大小,不同的w产生不同的决策方案序,决策方案序w·v不同,导致w·v和pj·v之间的相符度不同。均衡策略剖面σ*是指各个决策方案序w·v和指标序pj·v之间具有较好的相符度,即收益。

(10)

2.2 粒子群优化算法
粒子群优化算法(Particle Swarm Optimization)是通过模拟群鸟寻找食物得出的一种基于群体合作的最优搜索算法。优化算法过程中每个优化问题的解都是空间中的一个粒子,所有粒子都会通过适应度函数解出当前粒子位置的适应度函数值,同时每个粒子还有一个速度决定粒子飞行的方向和距离,最后鸟群会根据全体最优适应值不停地更换飞行的速度和方向,在解空间中搜索得出最优值。粒子群算法具有搜索速度快,搜索效率高,算法较为简单,适合实值型等优点。
求解均衡剖面σ*的粒子群算法的流程如下:

Step2: 定义适应度函数fitness-gbest(σ),种群中单个粒子的适应度便是剖面收益,即收益h(σj)=fitness-gbest(σj);
Step3: 初始化粒子群个体pop,计算各粒子历史最佳适应度,单个粒子的最佳历史位置,种群最佳历史位置,种群最佳历史适应度;
Step4:判断迭代次数是否满足设定的迭代次数,是则停止搜索,输出最优的结果,否则继续循环;
Step5:继续循环,对速度进行更新:
(11)

(12)
粒子元素的位置变化范围和速度变化是有一定的界限的,分别被限制在[Xdmin,Xdmax]和[Vdmin,Vdmax]中,若某一维粒子元素id或id超出边界值,则把超出边界的令其等于边界值;
Step6:通过更新后的粒子位置空间和移动速度,得出每个粒子新的适应度,通过与上一代适应度进行比较,大于上一代适应度,则对粒子最佳适应度进行更新,同时更新粒子历史最佳位置,如果小于上一代适应度,则保留粒子历史最佳适应度和历史最佳位置。同时求解种群最佳历史位置和最优适应度;
Step7:跳转至Step4。
3 示例验证及分析
在应召反潜的背景下,分别使用方案u1、u2、u3、u4对海域中的敌方潜艇进行搜索,方案u2、u3以扩展圆阵为例,方案u1、u4以圆形包围阵为例,利用Monte Carlo模型,仿真5 000次,得出了各个方案的搜潜效能,如表1所示。

表1 各方案的搜潜概率
通过表1可以发现,搜索能力u3>u4>u2>u1。在搜潜能力、隐蔽能力、跟踪及定位能力、经济性4个评价指标中,对潜搜索能力可以根据各设备组合方案的搜潜概率作为衡量标准,其他方案指标值可由专家给出评价,表2为各个方案因素指标。

表2 各方案因素指标
为了对表2进行定量分析,便于后续的数学计算,本文引入评判标度,将表2中的评判语言进行数字化转换,评判标度如表3所示。

表3 评判语言与评判标度的对应关系
通过表3的评判标度将表2转化为表4,表4也是决策矩阵A(yij)m×n。
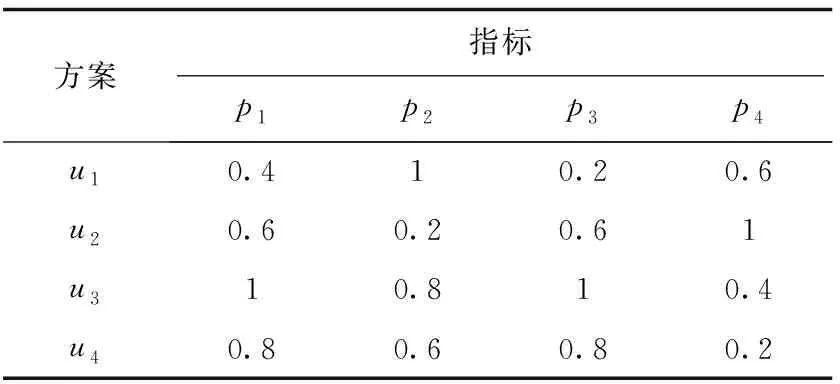
表4 转换结果
由于在求取相符度和均衡策略剖面时均是以收益为衡量标准,因此将评估矩阵A(yij)m×n规范化为矩阵R(rij)m×n时,按照指标集属性为效益型来处理,根据效益型指标集处理方法得到规范化矩阵R(rij)m×n,如表5所示。
1) 确定方案指标序。对于规范化矩阵R(rij)m×n,可以得出最直观的指标方案序如下所示:
a) 指标p1:指标方案序为u3>u4>u2>u1;
b) 指标p2:指标方案序为u1>u3>u4>u2;
c) 指标p3:指标方案序为u3>u4>u2>u1;

表5 规范化矩阵R(rij)m×n
d) 指标p4:指标方案序为u2>u1>u3>u4。
2) 求解均衡策略剖面:利用粒子群优化算法计算均衡策略剖面σ*时,相符度函数为适应度函数。求取相符度函数值时需要序位权值,如表6所示。

表6 序位权值
经过不断的迭代,以指标p1为例,得出了最佳适应度和平均适应度随迭代次数变化情况,如图2所示。
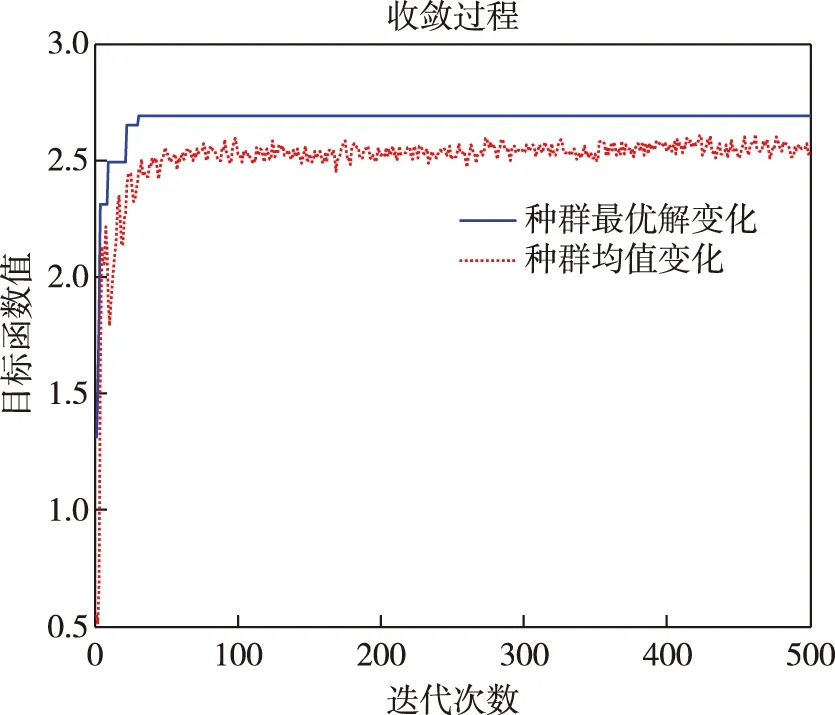
图2 经过500次迭代后的最优解和种群均值


(13)


表7 不同指标的相应参数
4)计算决策方案序。使用均衡策略剖面σ*对矩阵R(rij)m×n进行聚合,获得综合指标值z1=0.645,z2=0.427,z3=0.660,z4=0.410。根据综合指标值可以确定决策方案序w·v为u3>u1>u2>u4。
5)计算相符度。计算σ·v与指标序pi·v之间的相符度:
a)指标p1:Homo(σ·v,p1·v)=2.259;
b)指标p2:Homo(σ·v,p2·v)=0.941;
c)指标p3:Homo(σ·v,p3·v)=2.690 4;
d)指标p4:Homo(σ·v,p4·v)=0.800。
根据决策方案序w·v,舰机多设备组合方案搜潜的最优方案序为u3>u1>u2>u4,由4个指标因素得出的指标方案序中,指标p3确定的方案序u3>u4>u2>u1与最优方案序相符度较高,可作为舰机多设备组合搜潜的参考依据。在搜潜过程中,u3方案最佳,u1方案最差,因此优先选择u3组合进行搜潜。
在实际的搜潜过程中,吊放声呐与拖曳声呐组成的双基地联合搜潜模型可以提高搜潜效能,吊放声呐单基地搜潜时,搜潜效能要低于双基地搜潜。由于声呐浮标的被动工作方式,导致了其搜潜效能不佳,并且由于浮标的不可回收性,导致了u1方案的经济性较差;u4方案虽然可以提高搜潜效能,但由于浮标的不可回收性,导致其经济性不理想,而u3方案兼顾搜潜概率的同时,也具有很高的经济性,因此方案u3最佳。
4 结束语
本文根据现阶段搜潜的具体情况,建立了舰机多设备组合的搜潜方案,并且根据实际搜潜状况,给出了评价指标集。基于博弈理论,研究了多设备组合搜潜博弈分析算法,给出了求解多设备组合搜潜方案博弈模型均衡剖面的粒子群优化算法。以当今主流的搜潜设备为例,通过计算得到了各方案未知权重下组合的排列顺序,验证了本次决策方法的可行性和正确性。博弈分析结果表明:舰机多设备组合搜潜方案分析方法能够在权重等重要信息未知的情况下,通过博弈分析得出均衡策略剖面,然后根据均衡策略表面得出指标间的收益,进一步确定多方案的优先序列,为解决不确定条件下舰机多设备组合搜潜分析提供新的参考。
——工程地质勘察中,一种做交叉剖面的新方法

