用宽带超表面产生阵列贝塞尔光束
陈 磊,陆 菁,文 静
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.中科信工程咨询(北京)有限责任公司,北京 100032)
引言
理想的贝塞尔光束是一种无衍射光束,它是自由空间亥姆霍兹方程的一组解,由Durnin等在1987年发现[1]。环形狭缝和透镜(相距一个焦距)组成的简单光学系统[1],衍射光学元件(diffractive optical elements,DOE)[2],锥透镜[3]和空间光调制器(spatial light modulator,SLM)[4]等传统方法可以用来产生贝塞尔光束。和生成单个贝塞尔光束相比,阵列贝塞尔光束能够增强贝塞尔光束的某些应用的适用性,例如阵列贝塞尔光束在细胞转染应用中可以节省时间[5],对细胞进行高分辨率实时3D成像应用中能够提高扫描效率[6]等。通过将达曼光栅相位和锥透镜相位结合并加载到SLM上可以产生从中心发散的等强度阵列贝塞尔光束[7]。使用多个不同中心点的锥透镜相位全息图,并将其不同部分合并加载到SLM上能够产生等强度的阵列贝塞尔光束[8]。然而由于经典的SLM具有比可见光波长大一个数量级的像素尺寸,这限制了相位梯度的可用范围。通过周期性排列的圆锥形聚合物也能形成贝塞尔光束阵列[9],不过传统的圆锥形聚合物具有有限的数值孔径,且由于聚合物的顶端不是一个理想的圆锥,这会影响贝塞尔光束的质量。
本文设计了一种超薄的全电介质光学器件以克服以上限制,并通过FDTD软件验证了该器件的可行性。和基于达曼光栅原理产生的贝塞尔光束阵列不同[10],本文设计的器件产生的贝塞尔阵列均平行于入射光,该器件由亚波长尺寸像素点的电介质超表面构成。近年来,已经开发了大量基于超表面的光学器件,例如高效率的平面波片[11]、全息成像[12−16]、平面透镜[17−20]和无衍射光束发生器[21−25]。在本项工作中,将具有不同中心点的两个锥透镜相位的不同部分相结合,经过几何相位调制[26−27],得到了一种可以宽波段工作的阵列贝塞尔光束发生器。
1 设计的原理和方法
1.1 周期性纳米柱的特性
琼斯矩阵理论可以用来描述电磁波在超表面晶胞中的各向异性光学特性[28]。具有任意偏振态的入射光 |Einc〉 照射纳米柱产生的输出光由三个偏振分量组成:


图1 硅纳米柱的偏振转换效率Fig.1 Polarization conversion efficiencies for silicon nanopillars
超表面晶胞如图1(a)所示,它由二氧化硅基底和长方体硅结构组成。单个硅结构的长(L)、宽(W)、高(H)和旋转角度分别为180 nm、90 nm、380 nm和θ,超表面晶胞的周期P为250 nm。为了充分发挥贝塞尔阵列光束发生器的性能,本文将超表面单元设计为亚波长尺寸,通过改变单个立方柱的旋转角度θ,可以得到所需要的相位轮廓,θ的旋转角度范围为0~180°。单个晶胞在不同波长处的偏振转换效率如图1(b)所示,由于本文采用左旋圆偏振光作为入射光,此时偏振转换效率由出射光中总的右旋圆偏振光功率除以入射光的总功率得到。为了使单个结构的偏振转换效率最大化,单个纳米柱的长、宽、高和周期是由时域有限差分算法(FDTD)优化得到。在波长从580 nm到800 nm范围内,单个晶胞的偏振转换效率都超过了57%,在波长为663 nm处的偏振转换效率达到了84%。在单个晶胞的仿真中,沿x轴和y轴方向施加了周期性边界条件,沿z轴方向施加了完美匹配层(PML)。仿真中用的硅材料在波长580 nm、690 nm和800 nm处的折射率分别为4.00、3.80和3.69。
1.2 设计用于产生贝塞尔阵列的超表面器件
贝塞尔光束相位在二维空间的函数为[21]
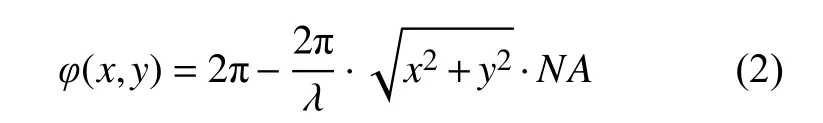
式中:λ为入射光波长;NA=sin(θ),θ为光线的折射角度;,r为径向坐标。NA值决定了贝塞尔光束的半高全宽,相位的总宽度D和无衍射距离。NA值越大,半高全宽越小。增大锥透镜相位的总宽度D,贝塞尔光束的无衍射距离会变长,减小NA值也会增加贝塞尔光束的无衍射距离。
在SLM上加载复杂的全息图可用于产生贝塞尔光束阵列[8],在SLM上加载一张相位图可以在3D空间中产生280个独立的焦点[29]。该相位图由可以在空间两个不同平面处分别产生100个焦点和180个焦点的两张相位图相加得到。借鉴以上两种方法,本文将向左偏移4μm的锥透镜相位乘以一个相同尺寸的二进制随机相位,得到了随机相位1,如图2(a)所示。图2(b)展示的相位是由向右平移4 μm的锥透镜相位和第一个随机相位的二进制补码相乘所得。图2(c)展示了本文设计的最终相位,它由相位1和相位2相乘得到。图2(c)中D为总相位图的直径。

图2 用于生成贝塞尔光束阵列的复用相位Fig.2 Multiplexed mask for generation Bessel beam array
当左旋圆偏振光入射时,通过改变位置(x,y)处纳米柱的旋转角度将总相位编码到电介质超表面上,每个纳米柱的旋转角度 θ(x,y)=φ总(x,y)/2,φ总为总相位。相位1和相位2在设计波长700 nm处的NA值都为0.3,NA值随着波长的变化而产生改变。部分超表面器件的俯视图如图3所示,所有纳米柱以直角坐标系排列且每个纳米柱的长宽高都保持一致。超表面器件总的直径为40 μm,高度为380 nm。

图3 用于生成贝塞尔光束阵列器件的俯视图Fig.3 Top view of the Bessel beam array generator
2 结果和讨论
当左旋圆偏振光照射本文所设计的超表面器件时,无需额外加一个透镜对阵列光束进行准直,就会产生两个相互平行的贝塞尔光束。由于几何相位的独特性质,本文中的器件可以宽波段工作。由于单个晶胞在波长从580 nm到800 nm内的偏振转换效率都大于57%,且当波长小于580 nm或者波长大于800 nm时,单个晶胞的偏振转换效率会急剧降低,所以本文仅展示了该器件在波长从580 nm到800 nm范围内的四个波长处的光场强度分布。不同波长的光入射该器件所得到的xz截面的光场强度分布如图4所示。图4(a)、(b)、(c)和(d)分别展示了在波长580 nm、663 nm、747 nm和800 nm处xz截面的光场强度分布。两个贝塞尔光束之间的距离为7.8 μm,基本符合理论设计值8 μm。阵列贝塞尔光束的无衍射距离随着波长的增大而变短,这是因为超表面器件的大小不变,当波长增加时,NA值会逐渐变大,所以贝塞尔光束的无衍射距离会随着NA值的增大而减小。贝塞尔光束的无衍射距离l由下式给出

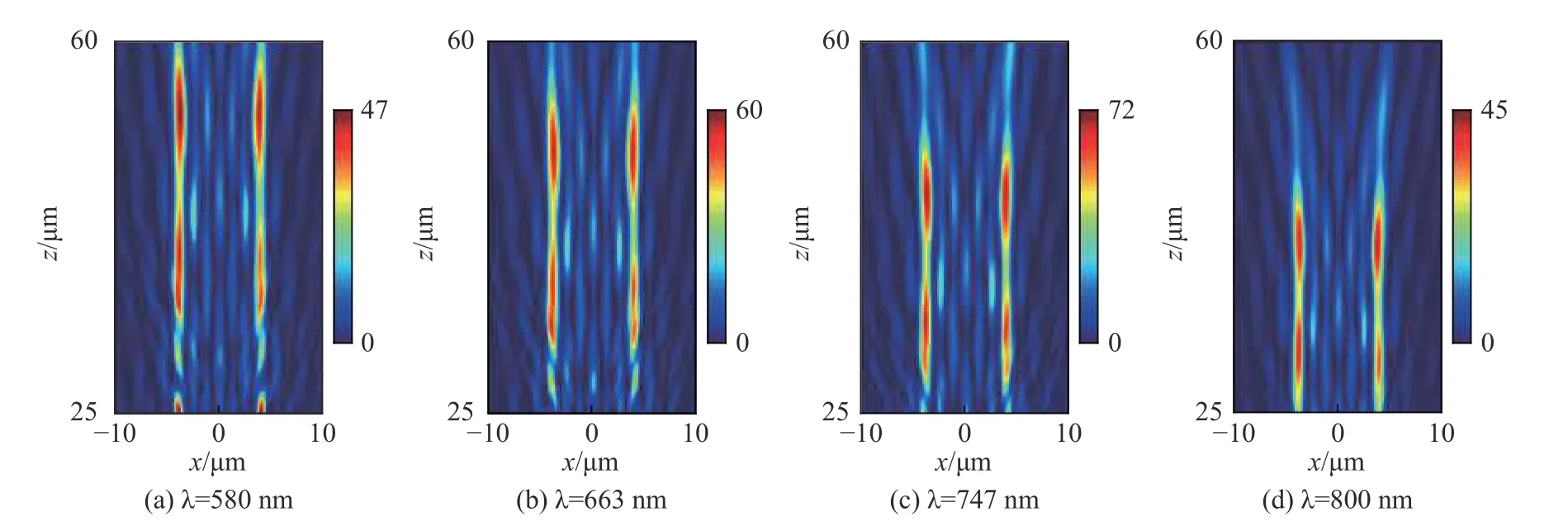
图4 阵列贝塞尔光束沿z轴方向的强度分布Fig.4 Intensity profile of the Bessel beam arrays along the z-axis direction
受单个晶胞偏振转换效率的影响,各个波长处所产生的阵列贝塞尔光束的强度值各不相同。仿真中用到的左旋圆偏振光由两个振动方向相互垂直、相位差为90°且振幅都为1的线偏振光合成。从图4可以看出,波长为747 nm时单个硅结构的偏振转换效率最高,波长为800 nm时单个硅结构的偏振转换效率最低。相对应的,波长为747 nm时器件产生光束的峰值强度最高,波长为800 nm时器件产生光束的峰值强度最低。
贝塞尔光束在非衍射方向z轴上传播的场分布表示为

式中:A为振幅;r为径向坐标;φ为相位;kz和kr为满足等式(其中λ为波长)的相应纵向和横向波矢量。由于贝塞尔光束的横向光场强度分布由kr决定,其中。在本文的设计中,根据参考文献[21],y,λ),其中φ如式(1)所示,此时kr=∇φ(x,y,λ),而基于几何相位设计的超表面器件的相位梯度和波长无关,因此,本文中基于几何相位设计的超表面器件所产生的阵列贝塞尔光束的横向光场强度分布和波长无关[21]。本文仅展示了一个波长处xy截面的光场强度分布。波长为580 nm的左旋圆偏振光照射超表面器件时,在z为50μm处得到的xy截面的光场强度分布如图5(a)所示。和基于达曼光栅原理产生的阵列贝塞尔光束不同[7−11],本文设计的阵列贝塞尔光束中的每个光斑都由单独的锥透镜相位产生。图5(b)展示了图5(a)白色虚线处的归一化强度。所形成的两个光斑的强度几乎一致,并且基本关于x轴对称。这是由于本文设计用于产生两个贝塞尔光束所对应的相位也是关于x轴对称的,且编码两个相位的超表面结构的大小也完全一致。通过改变锥透镜圆心的位置能够得到具有不同位置的阵列贝塞尔光束。在两个相位上编码具有不同NA值的锥透镜相位可以得到具有不同尺寸的阵列贝塞尔光束。由于改变单个结构的长、宽、高可以得到不同的偏振转换效率[30],所以在两个相位上编码不同的超表面结构得到不同强度的阵列贝塞尔光束,还可以用超表面编码多个锥透镜相位得到含有多个贝塞尔光束的阵列。
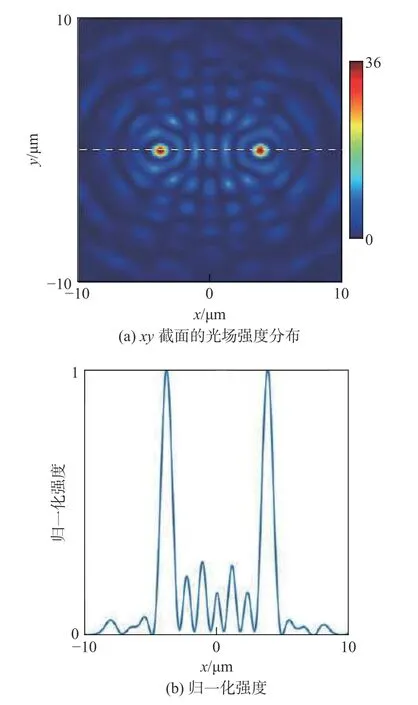
图5 阵列贝塞尔光束在xy截面的光场强度分布Fig.5 Intensity profile of the Bessel beam arrays in the xy plan
3 结论
作为用微型锥透镜阵列或在SLM加载多个锥透镜相位来产生阵列贝塞尔光束的替代方案,本文提出了用超薄超表面器件来产生阵列贝塞尔光束的一种新方法。本文通过时域有限差分算法(FDTD)验证了该器件在波长从580 nm到800 nm的范围内可以有效的工作。该器件在不同波长处产生的阵列贝塞尔光束都垂直于超表面并且每个光斑的强度基本一致。和以前用来产生阵列贝塞尔光束的方法相比,本文提出的方法显示许多重要的优点,例如全电介质超表面的优势,使器件具有亚波长像素尺寸和宽带特性。本文设计的器件对入射光的偏振比较敏感,潜在的后期工作计划可以研究偏振不敏感且高效率的惠更斯超表面。我们期待本文提出的关于阵列贝塞尔光束的设计方法,能激发关于各种类型阵列光束的设计与应用。

