单张平面圆图像的空间圆心快速提取方法

姚海滨，翁金平，程筱胜，姜 伟，沈 静

1.扬州市职业大学 电气与汽车工程学院, 江苏 扬州 225009

2.南京航空航天大学 机电学院，南京 210016

1 引言

随着计算机技术与测绘技术的发展，光学三维测量技术得到了越来越广泛的应用[1-2]。在该过程中圆形目标圆心空间坐标的精确快速提取是影响测量精度和效率的一个重要方面。

多种研究资料表明，目前空间圆心坐标提取主要依赖立体视觉方法，首先提取出椭圆中心，再利用双目成像原理求解出空间圆心坐标[3-5]，由于透视投影变换该过程中椭圆中心往往并不是空间圆心的投影点，因此重建出的空间圆心坐标精度不高，尤其是面对大型圆心目标时这个问题尤为明显。针对该问题很多学者提出了多种解决方法，主要分为两类[6-7]：一是畸变补偿法，即根据已知标记点与像平面的夹角以及标记点与像平面的距离分析设计给出圆心补偿的数学模型，根据该数学模型对提取出的椭圆圆心进行补偿，该方法虽然在仿真中得到验证，但是标记点与像平面的姿态信息在实际应用中很难获取到，因此该方法在实际应用中受到了很大的制约，在实际应用中意义不大；二是利用非线性优化方法优化位姿，即拍摄两个视角图像，根据极线匹配求解出相机姿态变换，再根据初始姿态进行边缘轮廓的重投影，构建最小二乘模型使边缘重投影误差最小化，该方法需要在两个视角图像下对边缘进行匹配，而椭圆边缘依靠极线匹配得到的效果并不好；文献[8]提出了基于对偶二次曲线的方法求解圆心，根据共面的3个标志点求解任意两个圆心之间的圆心投影向量，再通过向量叉乘求解圆心投影，该方法从一定程度上提高了圆心提取精度，但是需要标志点共面，且至少需要3 个不共线标志点，实际测量中很难保证标志点共面，且提取圆心三维坐标时也需要两个视角的图像。总体来说，目前的方法都需要多个视角图片或者多个标志点才能完成圆形目标中心三维坐标的提取[9-10]，且精度不可靠，尤其在依靠大型圆形目标定位应用，比如机器人定位[11-12]、圆形管道测量[13-14]等需求中难以取得较好效果。

针对上述问题，本文提出了一种基于单张平面圆图像的空间圆心快速提取方法。该方法利用相机光心与成像椭圆构建了空间圆锥方程，再构建出圆锥正底面，根据正底面求解出空间圆的平行平面方程，最后根据平行平面与实际半径找出正确空间圆方程，避免了空间圆心投影坐标求解问题，且只需单张图像即可求解出空间圆心坐标，该方法稳定可靠，本文首先给出了算法步骤，并且进行了完整的推导，最后给出了算法分析与实验验证。

2 算法推导

圆形目标成像模型如图1 所示，E点为视点，EXeYeZe为相机坐标系，P点为相机主点，P-XpYpZp为图像坐标系。圆锥曲线是由平面与二次锥面相交得到的曲线，该曲线具有镜像对称的特性，根据圆锥曲线理论以及上述成像模型有以下两个结论：

（1）存在唯一锐角θ，圆锥正底面绕长轴顺时针逆时针旋转θ可得两个圆截面；

（2）若平面A与圆锥交线为圆，对于任意平行于平面A的平面B，若存在交线，则该交线为圆。

图1 成像模型

根据以上结论，可以通过以下步骤求得空间圆心坐标：

（1）构建圆锥正底面；

（2）将底面所在平面绕长轴旋转，找到截面为圆的θ角，记此时平面为α；

（3）寻找与α平行且截面圆直径为D的平面β；

（4）求解此时截面圆方程，求解圆心坐标。

上述步骤中包含了椭圆锥方程的求解以及椭圆锥与平面方程交线的求解，具体计算过程推导如下。

2.1 椭圆锥一般方程

2.1.1 图像坐标系下椭圆锥方程

假设在图像坐标系P-XpYpZp下椭圆锥方程为为3×3对称矩阵，为3×1向量，为标量。取A=[aij]，B=[bi]，c=1 ，由于椭圆在XOY平面，那么y2为 0，此时令Q(Y)=0 可得：

由椭圆的标准方程式（2）可知，假设椭圆长轴半径为d0，短轴半径为d1，则在椭圆锥顶点处梯度为 0，即且Eˉ在椭圆锥上，则有，联立之可得如式（3）所示：

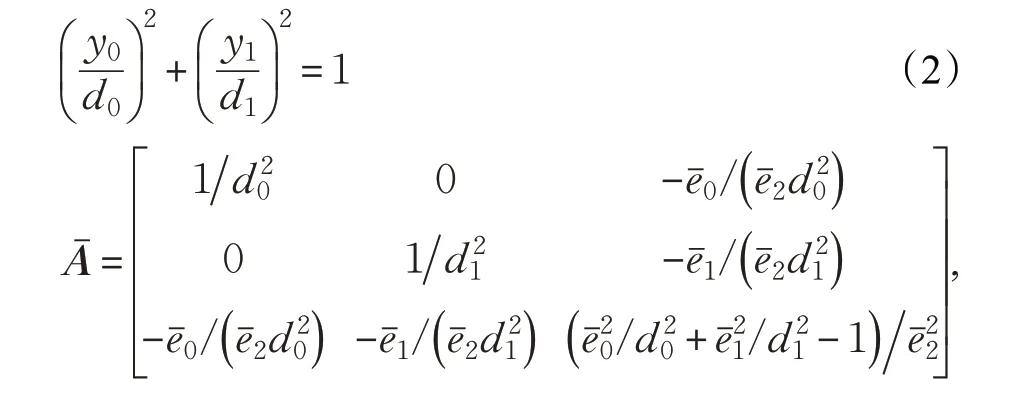
2.1.2 相机坐标系下椭圆锥方程

假设图像坐标系在相机坐标系下的一组标准正交基为Re=[Ue Ve Ne]，Re也可看作两个坐标系间的旋转变换矩阵，假设Ce为盘面上某一点在相机坐标系下坐标，X为图像坐标系下椭圆坐标，Y为相机坐标系下椭圆坐标，则有：

因此一般椭圆锥方程推导如下：

其中：

2.1.3 任意平面与椭圆锥交线方程

假设存在投影平面其原点为Cp，单位法向量为Np，构建其余两个正交单位向量Up和Vp，则旋转矩阵为Rp=[Up Vp Np]该平面与椭圆锥相交，该交线为椭圆，则该椭圆上点可由Xp=Cp+y2Up+y3，Np=Cp+JpYp表示，该椭圆方程推导如下：

椭圆方程可以重构为如下形式：

2.2 构建正底面

由椭圆锥对称性易知，圆锥顶点与正底面圆心连线必然垂直于正底面。如图2所示，在投影轮廓上任取一点c1，以c1为原点，直线c1E为法向量方向构建平面π1，交圆锥于椭圆l，根据本文2.1节算法求出圆心坐标c2，判断连线c2E与平面法向量是否夹角小于门限值，该门限值一般取e-6，若不满足则继续以c2E为法线构建平面与圆锥求交，直至找到正底面。

图2 构建正底面

2.3 求解圆形目标平面

将正底面所在平面绕长轴旋转θ角，记旋转后的平面为α，平面α与椭圆锥相交于椭圆，根据2.1节可求出该椭圆长短轴半径，以最小增量Δθ扰动该过程如式（9）所示，其中η表示学习率，用以控制扰动步长，构造最小二乘问题寻找参数θ使椭圆长短轴半径相差最小，如式（10）所示：

通过上述步骤可以求得交线为圆时平面方程，记该平面为β，原点为圆心坐标c，易知圆形目标中心必然在射线Ec上，假设该中心距离c点距离为l，那么该坐标为根据线性变换可求得该点坐标，以该点为原点构造平行于平面β的平面β′，根据2.1 节可求出β′与椭圆锥相交圆直径d，已知圆形目标直径D，那么可构造最小二乘问题如下：

通过迭代可求得正确l值，继而求得空间圆形目标方程与圆心坐标。而根据结论（1），存在顺时针与逆时针两个旋转角，具体表现为不能确定相机方向，而该二义性可以由实际圆心投影坐标与投影椭圆圆心相对位置排除。

3 算法分析与应用

3.1 参数讨论

2.3 节中参数η表示学习率，该参数一般称为超参数，易知2.3节中问题属于凸优化问题，因此利用梯度下降法一定可以求得极值，式（12）是一元函数，其导函数形式比较简单，如式（13）所示，而导函数本身表示了沿l方向的梯度方向，结合梯度下降法可以求得极值，而学习率η影响了梯度下降的速度。

实验表明，当η取值为常数时，即以恒定步长扰动最小二乘模型时，若取值较小则收敛较慢，若取值较大则会出现震荡收敛的情况，如图3 所示，而η随着求解过程逐渐衰减则能取得较好效果，起始下降速度较快，随着学习率的衰减逐渐收敛到最小值，迭代次数也较小。

图3 学习率分析

3.2 应用分析

3.2.1 管道长度测量

图4所示设备为管道测绘仪与管道检测机器人，测绘仪用于静态测量场景，而管道检测机器人则用于狭窄空间下的管道测量，两台测量设备均包含了照明装置与相机。

图4 管道测绘设备

相机由张氏标定法[10]完成内参标定，本文以实物管道测量与三维仿真环境作对比，管道长度2 m，管道口径已知为0.4 m 利用本文算法分别求出两端圆形端口中心坐标，再求出管道长度，多个角度求解20 次，统计数据如图5 所示，可见本文算法能准确求解出管道长度，实际测量平均误差在2 cm左右，而数据中实际测量方差要大于仿真环境测量方差，这是因为在实际环境中圆形目标边缘噪声较多，提取精度低于仿真环境，而在实际测量中也可以多测测量求平均来降低测量值方差。

3.2.2 圆心投影提取精度测量

为测量本文方法提取圆心精度，将如图6所示的标志圆作为靶标进行测试。

图5 管道测量

图6 圆形靶标

待测圆的半径为5 cm，中间角点即为实际圆心，在像平面与靶标平面呈45°夹角时在不同距离采集图像，并提取到角点亚像素坐标作为基准，利用本文方法求解出圆心三维坐标并通过相机模型投影到成像平面后得到像素坐标，再提取出外圆的所有亚像素轮廓坐标进行椭圆拟合[15]，将拟合出的圆心与本文结果作对比。图7 为靶标检测结果，白色部分为检测出椭圆轮廓，蓝色标记点为椭圆中心，矩形标记点为本文算法求解中心。

图7 靶标检测结果

三者结果如表1所示，本文提取的圆心坐标与基准坐标相差大概0.1～2 个像素，但是椭圆中心与基准相差了5～12 个像素，因此本文方法所求得的圆心坐标更精确，与实际坐标误差非常小。

表1 圆心坐标对比结果pixel

4 结语

本文针对目前圆心目标圆心空间坐标提取精度与效率低的问题，提出了一种基于单张平面圆图像的空间圆心快速提取方法。首先利用相机光心与成像椭圆构建了空间圆锥方程，再构建出圆锥正底面，根据正底面求解出空间圆方程，最后根据平行平面与实际半径找出正确空间圆方程，避免了空间圆心投影坐标求解问题，且只需单张图像即可求解出空间圆心坐标，方法稳定可靠，在机器人定位与圆形管道测量等问题中均具有较好的实用性。本文方法也可以应用于摄影测量领域，利用多个视角观测数据进行光束法平差，提高测量精度。