基于Schatten-p范数和特征自表示的无监督特征选择

彭 明，张海澎

1.龙岩学院 数学与信息工程学院，福建 龙岩 364012

2.国网山西省电力公司 沁源县供电公司，山西 长治 046500

1 引言

随着科学技术的快速发展，各应用领域收集的数据量越来越大，而这些数据往往具有高维特征，并且含有大量噪声和冗余信息。直接对这些高维数据进行建模学习，通常会有预测效果低、数据陷入“维数灾难”等问题。为了解决这些问题，现有的模型算法通过利用高维数据中固有的一些关联结构，例如数据的流形结构和低秩结构等，来提高模型的预测效果；通过特征选择方法有效地选出高维数据的重要特征，去除大量不重要的噪声和冗余特征进而避免“维数灾难”问题。同时，在现实世界中存在大量的无标签高维数据，对这些数据进行标记是昂贵和耗时的，甚至是不可行的。因此，对高维数据进行无监督特征选择算法[1-2]的研究是有很大现实意义的。

近年来，国内外许多专家学者基于高维数据中固有的流形结构和低秩结构对无监督特征选择算法进行了大量的研究。基于拉普拉斯打分特征选择LS[3]将数据的流形结构运用到无监督特征选择模型中，即利用高维流形上数据点间的近邻结构在低维嵌入中得以保持的特性，构建的近邻图，独立计算每个特征的得分进而选择特征；为了得到判别性的特征子集，文献[4]将谱聚类方法和流形结构结合在一起，提出了基于非负谱分析的无监督特征选择算法NDFS；针对基因表达数据，文献[5]提出了基于谱聚类的无监督特征选择算法FSSC，对所有特征进行谱聚类，将相似性较高的特征聚成一类，并定义特征的区分度与特征独立性来度量特征重要性，从各特征簇选取代表性特征，构造特征子集；基于鲁棒谱学习的无监督特征选择算法RSFS[6]提高了图拉普拉斯嵌入和稀疏谱回归的鲁棒性，进而降低了原始数据中因噪声和冗余特征对构建的图拉普拉斯的影响；根据不同的稀疏正则化方法，基于最大熵和ℓ2,0范数约束的无监督特征选择算法ENUF[7]使用了具有唯一确定含义的ℓ2,0范数等式约束来确定选择特征的数量，并结合谱分析探索数据的局部几何结构和基于最大熵原理自适应的构造相似矩阵；在保持流形结构下，嵌入式的无监督特征选择算法EUFS[8]通过稀疏学习将特征选择直接嵌入到聚类算法中，不需要伪标签的转换；基于重构的无监督特征选择算法REFS[9]是根据数据重构误差准则，将特征相关性定义为特征通过重构函数逼近原始数据，并结合重构后的流形结构保持，进而选择重要的特征；文献[10]在保持流形结构下，运用拉普拉斯矩阵的特征向量和特征值得到具有代表性的特征子集；文献[11]运用自表示方法[12]形式化特征选择算法，结合低秩近似、结构学习和稀疏正则，提出了基于低秩近似和结构学习的无监督特征选择算法LRSL，并根据Ky Fan定理对低秩进行凸优化求解；基于图学习和低秩约束的无监督特征选择算法[13]运用对系数矩阵的低秩约束控制流形结构进而减少冗余特征对性能的影响；文献[14]整合了特征选择和特征提取两种降维方式，提出了基于低秩嵌入和对偶拉普拉斯正则的无监督线性特征选择映射算法FSP，运用系数矩阵的低秩约束去重构样本点；已有算法大都运用的是流形结构中的单边信息，文献[15]提出了基于低秩稀疏非负矩阵分解的对偶无监督特征选择算法NMF-LRSR，运用低秩稀疏表示去重构拉普拉斯图，在特征选择过程中考虑数据的局部和全局结构，进而使选择的特征子集更为精确。

然而，已有的算法大都是基于凸优化的目标函数，本文基于高维数据中固有的低秩结构，提出了一种基于Schatten-p范数和特征自表示的非凸无监督特征选择算法（SPSR）。首先运用特征自表示重构无监督特征选择问题中的系数矩阵，其次结合Schatten-p范数正则项逼近秩最小化问题，即低秩结构，然后使用增广拉格朗日乘子法和交替方向法乘子法框架对目标函数进行优化，同时运用奇异值分解方法对Schatten-p范数近似的秩最小化问题进行优化求解。最后在6 个公开数据集上与RSFS算法、EUFS算法、REFS算法、LRSL算法等经典的无监督特征选择算法进行实验比较，证明本文提出的基于Schatten-p范数和特征自表示的无监督特征选择SPSR算法是有效的。

2 问题形式化

先介绍一下本文中使用的一些符号，其中，大写粗斜体表示矩阵，小写粗斜体表示向量。对于任意列向量它的ℓ2范数为对于任意矩阵，它的 Frobenius 范数矩阵的秩和转置分别用rank(M)和MT表示。对于任意方阵方阵A的迹为，可逆矩阵表示为A-1。In∈ℝn×n表示单位矩阵。

特征自表示是每个特征可以由其他的特征线性表示[12]，即，对于数据集X的每一个特征fi，有：

对于所有的特征向量，则有：

其中，#-范数 ‖ ⋅ ‖#表示某种残差度量，比如，Frobenius范数用来处理高斯噪声[16]，ℓ2,1-范数 ‖ ⋅ ‖2，1用于描述特定的样本异常点[17]，ℓ1-范数 ‖ ⋅ ‖1用来处理随机或者稀疏数据[18]。然而，当W是单位阵时，就会得到一个平凡解，即残差E=0。因此，为了指导特征子集的选择和避免平凡解，引入一个正则项R(W)，则无监督特征选择可以被形式化为：

其中，λ是用来权衡拟合精度和正则项的系数，且λ＞0。令W=[w1;w2;…;wd]，wi是系数矩阵W的第i行，wi是d维向量，且 ‖wi‖2可以表示第i个特征的重要度，则 ‖wi‖2的值越大，表示第i个特征越重要。

一方面，特征选择的目的是寻找一个低维的特征子集尽可能地刻画原来的特征空间，另一方面，已有研究表明噪声和冗余特征会导致数据矩阵的秩增大[19]，同时为了避免平凡解，引入低秩正则项来约束系数矩阵W。同时，Frobenius 范数可以利用低秩矩阵来近似单一的数据矩阵。则本文的无监督特征选择形式化为如下形式：

由于秩函数是非凸且不连续的，公式（5）是一个NP难问题，即无法在多项式时间内求解。为了解决这个问题，文献[20]中提出利用Schatten-p范数来逼近矩阵的秩。因此，公式（5）转化为如下问题，即，本文提出的基于Schatten-p范数和特征自表示的无监督特征选择SPSR算法的目标函数：

当σi=0 时，=0 ，否则=1。根据公式（7），可知也就是说，当p→0，近似等于矩阵W的秩。类似的，当p=1 时，矩阵W的Schatten-1范数为：

Schatten-1 范数又被称为核范数，记为 ‖W‖*。文献[21]用核函数作为秩最小化问题的最紧凸松弛，然而，基于核范数的模型会对数据的低秩成分进行过多的收缩。因此，用Schatten-p范数最小化问题逼近秩最小化问题[22-23]。同时，有理论证明[24]Schatten-p范数能够取得更好的效果。

3 算法模型优化

本章为基于Schatten-p范数和特征自表示的无监督特征选择SPSR 算法模型进行优化求解。首先，引入辅助变量M，将公式（6）转换为如下等价优化问题：

该优化问题可以用增广拉格朗日乘子法（ALM）算法有效地求解。优化问题（9）的增广拉格朗日函数如下：

其中，Y是拉格朗日乘子，μ＞0 是一个控制惩罚强度的惩罚参数。

本文通过交替方向法乘子法（ADMM）框架将公式（10）分解为若干子问题迭代求解W,M,Y,μ，具体迭代更新规则如下：

（1）固定变量M,Y和μ，更新变量W

关于W的优化问题可以等价转换为如下形式：

对任意矩阵A∈ℝn×d，有，同时，对于 任 意 矩 阵A1∈ ℝn×d和A2∈ ℝd×n，有 t rA1A2=trA2A1。则：

根据公式（12），对W进行求导，可得：

（2）固定变量W,Y和μ，更新变量M

关于M的优化问题，公式（10）可以等价转换为：

对上面式子做一下简单变换，得到：

根据矩阵M的Schatten-p范数的p次方则有：

为了便于对公式（16）的求解，引入文献[20]中的一个定理。

定理1对任意两个矩阵B,C∈ℝn×d，令σ(B)和σ(C)表示对角矩阵，其对角元素分别为矩阵B和C相同排序下的有序特征值，则有trBTC≤trσ(B)Tσ(C)。

根据定理1，有：

因此，根据公式（17）和公式（18），最小化公式（16）中的L(M)可以被简化为如下的最小化问题：

令δi≥0 是Δ的第i个对角元素，ai是的第i个对角元素，也就是说，δi≥0 和ai分别是矩阵M和矩阵A的第i个奇异值，则公式（19）可以等价转换为如下最小化形式：

用f(δ)表示公式（20）中的目标函数，即：

根据δ≥0 的约束，求得f(δ)的梯度如下：

继续求f(δ)的二次梯度，得到一个拐点如下：

根据以上公式，最小化问题（20）的最优解可以通过如下公式求得：

其中，ϖ是一次梯度函数f′(δ)=0 的解。

（3）固定变量W和M，更新变量Y和μ

矩阵Y的迭代更新公式为：

其中，惩罚系数μ的迭代更新公式为：

以上是运用增广拉格朗日乘子法和交替方向法乘子法框架关于SPSR 算法模型的求解过程，具体算法步骤如算法1所示。

算法1基于Schatten-p范数和特征自表示的无监督特征选择算法（SPSR）。

输入：数据集X∈ℝn×d（n个样本，d个特征），选择的特征个数m和两个参数p,λ。

1.初始化μ=0.1,ρ=1.3,μmax=108,Y=0,W=M=Id；

2.repeat

3.通过公式（14）更新W；

4.通过问题（16）的最优解更新M；

5.通过公式（25）更新Y；

6.通过公式（26）更新μ；

7. until 满足收敛条件

输出：降序排列 ‖wi‖2，i=1,2,…,d，选出前m个特征作为特征子集。

4 实验与结果分析

本章通过现实世界中的数据集来验证所提算法SPSR的有效性。

4.1 实验数据集

实验选用了6个现实世界中的数据集进行研究，相关数据集可从feature selection dataset（shttp：//featureselection.asu.edu/datasets.php）中获取。数据集的详细信息如表1所示。这些数据集包含了人脸数据集Yale 和PIE10P，基因表达数据集 ly mphoma、GLIOMA 和 T OX-171，数字识别数据集gisette。

表1 实验数据集描述

4.2 度量准则

为了验证算法的有效性，文中采用聚类精度（clustering accuracy，ACC）作为判断标准，来衡量不同算法选择不同特征子集时的效果，其中，ACC的值越大表示算法效果越好。

聚类精度（ACC）：

其中，n为样本数，l(xi)和l′(xi)分别为样本xi自带的类别标签和聚类算法得到的类别标签，δ(x,y)是指示函数，当x=y时，值为1，否则为0。

4.3 实验参数设计

为了验证所提算法基于Schatten-p范数和特征自表示的无监督特征选择SPSR的性能，实验比较了SPSR算法与基于鲁棒谱学习的无监督特征选择算法RSFS[6]、嵌入式的无监督特征选择算法EUFS[8]、基于重构的无监督特征选择算法REFS[9]、基于低秩近似和结构学习的无监督特征选择算法LRSL[11]，以及选择所有特征（Baseline）在表1数据集上的实验结果。

对比算法 L RSL、EUFS 和 R SFS 中关于ℓ2,1范数正则项和局部结构学习正则项的超参数均设置为1，LRSL中关于低秩近似的正则项超参数设置为1E4，同时RSFS中谱学习约束正则项和ℓ1范数正则项的参数均设置为1；对比算法REFS中惩罚没有被选择的特征重构错误的正则项和控制重构后保持原有特征结构的正则项参数均设置为0.1；4 个对比算法LRSL、REFS、EUFS、RSFS中涉及到的近邻数均设置为5；所有的实验将公式（6）中的正则化参数λ设置为，其中d是数据集的特征维数，Schatten-p范数中参数p设置为{0.1，0.2，…，0.9，1}。对表1 中所有的数据集，特征选择的个数设置为{20，30，…，100}。同时，实验选用K-means 算法进行聚类，而K-Means算法对初始选取的聚类中心点是敏感的，因此，K-means 算法对选取的特征子集运行30 次实验记录平均值。

4.4 结果分析

为了比较分析不同无监督特征选择算法的性能，表2和图1给出了不同算法的聚类精度。其中，表2给出了所有对比算法在不同数据集上的最大聚类精度，图1展示了所有对比算法的聚类精度与选择的特征个数的关系。从表2 中可以看出，所提算法SPSR 的聚类精度都高于保留所有特征（Baseline）的聚类精度，其中，在数据集 Y ale、lymphoma、GLIOMA 和 T OX-171 上，SPSR 比Baseline 的聚类精度高出5～8 个百分点，而在数据集gisette 和 P IE10P 上，SPSR 均比 B aseline 的聚类精度高出20个百分点。同时，除了lymphoma数据集上的聚类精度仅低于REFS 算法，所提算法SPSR 的聚类精度均优于其他对比算法。由图1 中算法的聚类精度与选择特征数量的关系可看出，所提算法SPSR在数据集Yale、gisette 和PIE10P 上的聚类精度均高于其他对比算法。尤其是，相对比于有低秩近似约束的LRSL算法来说，所提算法SPSR 无论选择特征的个数为{20，30，…，100}，在数据集Yale、lymphoma、gisette 和 P IE10P 上都以绝对的优势高于LRSL 的聚类精度；在数据集GLIOMA 和TOX-171上，所选择特征数在60个以内，所提算法SPSR均高于LRSL的聚类精度。说明了相对于LRSL中的低秩约束优化，所提算法SPSR 中的Schatten-p范数更能捕捉到数据集中真实的低秩结构。

综合表2和图1的对比信息可知，对比LRSL、REFS、EUFS、RSFS 等经典的无监督特征选择算法，本文所提基于Schatten-p范数和特征自表示的无监督特征选择SPSR算法的聚类效果更好。这也验证了，SPSR能选择出更有代表性的特征子集，同时也说明Schatten-p范数正则在特征选择算法中是非常有用的。

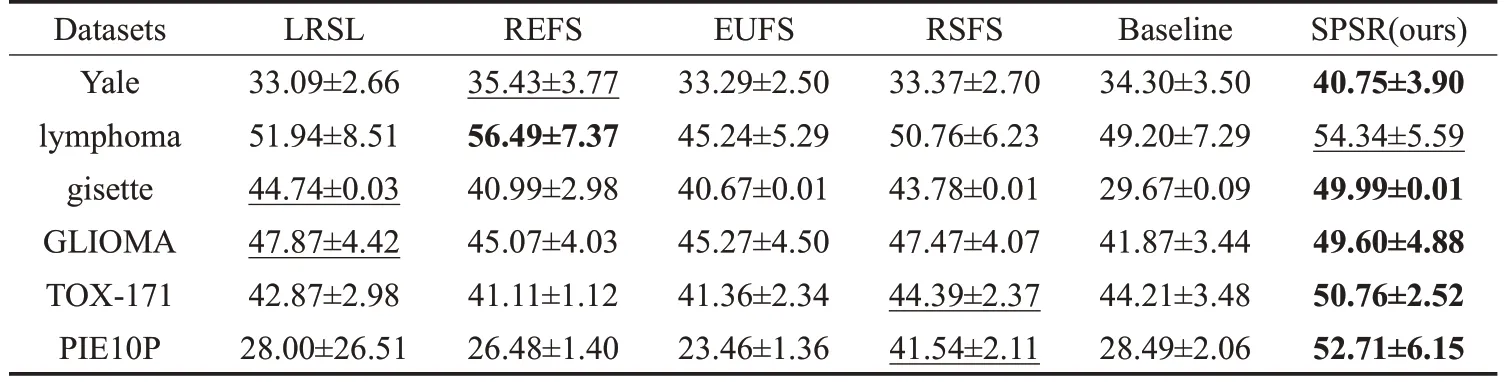
表2 在不同的数据集身上不同无监督特征选择算法的最大聚类精度（ACC±std）%

4.5 参数 p 和λ 的敏感性分析

参数p和λ是所提算法SPSR 中最重要的参数，本节分析它们对所提算法的影响。为了较好地展示SPSR 在不同参数下的聚类性能，只从一定范围内记录采样点的变化搜索区域。使用网格搜索策略，参数p的搜索区域为{0.1，0.2，…，0.9，1}，参数λ的搜索区域，其中d是相应数据集的特征维数。

图2展示了SPSR关于参数p的聚类精度，其中参数λ设置为d-1。从图2 中，可以看出除了数据集gisette，SPSR在其他5个数据集上在不同的p值处聚类精度是有所波动的。但SPSR在6个数据集上均在p=0.1 处得到较好的聚类精度，验证了参数p越低越逼近原始数据集的秩。

图3 所提算法SPSR关于参数λ 的聚类精度(p=0.1)

图3 展示了SPSR 关于参数λ的聚类精度，其中参数p设置为0.1。从图3中，可以看出数据集Yale和TOX-171在λ=d-1处取得较高的聚类精度，gisette、GLIOMA和PIE10P 在λ=d0处取得较高的聚类精度，lymphoma在λ=d-1/2处取得较高的聚类精度。也就是说，对于不同的数据集，SPSR 的目标函数中损失项和低秩正则项的平衡系数λ是不相同的。对于如何自适应获得不同数据集对应的平衡系数λ依旧是一个开放式的问题。

5 结束语

本文提出了一种Schatten-p范数和特征自表示的无监督特征选择SPSR 算法，通过特征自表示重构无监督特征选择中的系数矩阵，并运用Schatten-p范数正则项挖掘重构系数矩阵中真实的低秩结构，进而利用增广拉格朗日乘子法和交替方向法乘子法框架求解得到有效的特征子集。实验证明本文提出的SPSR算法是有效可行的。

所提算法SPSR为特征选择问题的研究提供了一个有趣的低秩近似方法，但在未来的研究中仍有一些问题需要解决，例如：SPSR算法能否整合数据固有的流形结构为统一的框架、能否根据数据集本身自适应地选择特征个数、如何有效地处理类别不平衡数据集，这些问题都将是下一步所关注和解决的问题。