参数动态调整的自适应布谷鸟算法

宋 钰，石立宝

电力系统国家重点实验室深圳研究室（清华大学深圳国际研究生院），广东 深圳 518055

1 引言

布谷鸟算法（Cuckoo Search algorithm，CS）是由学者Yang X S 和Deb S 于2009 年提出的一种智能优化算法，算法提出的灵感来源于自然界布谷鸟的寄生性育雏行为[1]。相比于其他智能优化算法，CS具有控制参数少、算法易实现、寻优路径优以及全局搜索能力强的优点[2]，近年来被广泛应用于优化[3-4]、预测[5-6]以及图像去噪[7]等领域。学者们针对布谷鸟算法展开了系统而深入的研究。文献[8]通过马尔科夫链模型证明了布谷鸟算法的收敛性。为克服布谷鸟算法后期收敛速度变慢、搜索能力降低的缺点，一些学者提出将布谷鸟算法与其他智能优化算法相结合，充分利用两种算法的优点以获得更佳的求解效果[9-11]。另外一些学者则致力于提升布谷鸟算法本身的性能。2011 年Valian E 等人提出了一种基于自适应机制的布谷鸟算法，通过动态改变布谷鸟算法中的参数提高了算法的局部和全局搜索能力，进而提升了算法的计算精度和收敛速度[12]。此后，国内外学者分别提出了多种动态改变布谷鸟算法参数的自适应机制。其中，部分研究依据当前迭代次数来改变该次迭代中各参数的大小[12-14]，另一些研究则依据每次迭代中各解的好坏来改变本次迭代中各解相应的参数[15-17]。这些研究在一定程度都取得了较好的改进效果。

本文首先简述了布谷鸟算法的基本原理。为了进一步提高布谷鸟算法的计算精度和收敛速度，本文在已有研究成果基础上提出了一种新的自适应布谷鸟算法。该算法可依据解的好坏来控制其发现概率的大小，并在运算初期依据迭代次数、解的好坏、种群规模和总迭代次数动态改变步长，在运算后期，不考虑迭代次数、种群规模的影响，仅依据解的好坏动态改变步长。最后，本文利用仿真实验对比了所提算法与其他算法的求解效果，证明了所提算法的优越性。

2 布谷鸟算法基本原理

布谷鸟算法的灵感源于布谷鸟的育雏行为。一些布谷鸟会将自己的蛋产入云雀、黄莺等宿主鸟的巢中，让它们代替自己育雏。由于布谷鸟蛋与宿主鸟蛋外表相似，往往不易被宿主鸟发现。当宿主鸟没有发现布谷鸟蛋时，它会同时孵化布谷鸟蛋和自己的蛋。由于布谷鸟蛋的孵化时间短于宿主鸟蛋，先孵化的布谷鸟幼雏本能地破坏鸟巢中的其他鸟蛋以获取更多的资源。当宿主鸟发现布谷鸟蛋时，它会抛出布谷鸟蛋或放弃整个鸟巢并选择其他地方重新筑巢。为了简化和模拟布谷鸟的育雏行为，学者Yang X S 和Deb S 提出了以下三条理想规则。

规则1每只布谷鸟每次只产一个蛋，并随机选择一个寄生巢来放置。

规则2在随机选择的一组寄生巢中，最好的寄生巢会被保留到下一代。

规则3可利用的寄生巢的数量是一定的，布谷鸟蛋被宿主鸟发现的概率为Pa。

此外，研究表明自然界中许多动物的觅食路径可以用 Lévy 飞行描述。Lévy 飞行是服从 Lévy 分布的随机搜索路径，由频繁出现的短步长和偶尔出现的长步长组成。在布谷鸟算法中，学者Yang X S 和Deb S 利用Lévy 飞行描述布谷鸟的飞行轨迹并更新鸟巢的位置。Lévy 飞行中大量的短步长有利于布谷鸟算法局部寻优，可以提高算法的搜索精度，同时少量的长步长可以扩大算法的搜索范围，有助于算法跳出局部最优。

将布谷鸟、宿主鸟巢以及布谷鸟蛋均看作解，则从自然界布谷鸟行为中抽象出布谷鸟算法的主要步骤为：

步骤1初始化各参数，随机生成一组初始解并计算它们的适应度。

步骤2通过Lévy飞行对解进行更新，如式（1）所示：

式中，xi(t)和xi(t+1)分别为第t次和t+1 次迭代时的第i个解，α是步长参数，Levy(β)代表遵循Lévy 飞行的随机步长。

步骤3比较新解的适应度值和旧解的适应度值，若新解的适应度值优于旧解的适应度值，则用新解替换旧解。

步骤4根据发现概率丢弃部分解，然后随机偏好游走生成同样多的解来代替被丢弃的解，如式（2）所示：xi(t+1)=xi(t)+r⊗Heaviside(Pa-ε)⊗(xk(t)-xj(t))（2）式中，r和ε为[0,1]区间内正态分布的随机数，Heaviside(u) 表示阶跃函数，Pa为发现概率，xk(t) 和xj(t)为第t次迭代时的两个随机解。

步骤5计算通过步骤2至步骤4产生的新一代的解的适应度值并挑选出最优解。

步骤6重复步骤2至步骤5，直到达到最大迭代次数。

3 改进的布谷鸟算法

在布谷鸟算法中，参数α控制每次迭代的步长δ（即变异量），并且α越大，步长δ越大。发现概率Pa控制产生新解的概率，并且Pa越大，产生新解的概率越大。而步长和产生新解的概率越大，每次迭代的搜索范围就越大，算法的全局寻优能力就越强，收敛速度也就越快。但随着搜索规模的扩大，算法的局部寻优能力会下降，算法的搜索精度也会下降。与之相反地，α和Pa越小，每次迭代的搜索范围就越小，全局寻优能力就越差，收敛速度也就越慢，但算法的局部寻优能力会增强，搜索精度也会提高。针对不同的优化问题，应选取适当的α和Pa以同时获取较快的收敛速度与较高的搜索精度。然而目前并没有一种系统的方法来确定α和Pa。此外，还应在较差解附近用较大的α和Pa全局寻优以提高收敛速度，用较小的α和Pa在较好解的附近局部寻优以提高搜索精度。而在传统的布谷鸟算法中，α和Pa为定值，不能根据解的好坏进行动态调整。针对以上问题，本文在文献[14-16]的基础上提出了步长δ和发现概率Pa的动态调整机制，令δ和Pa随着解的好坏、迭代次数的大小而自发地朝着合适的方向变化。

3.1 步长δ 的动态调整机制

假设优化问题的目标为求解函数最小值，xmin(t)和xmax(t)分别表示第t次迭代时的最优解和最差解，它们对应的适应度值分别为fmin(t)和fmax(t)，即第t次迭代时求解出的最小和最大适应度。则对于最差解xmax(t)，其步长δmax(t)应为一个很大的值。受到文献[18]思想的启发，δmax(t)可采用如下方式确定：

上述解的更新过程如图1 所示，其中a和b点分别代表。

图1 解的更新过程

而对于最优解xmin(t)，其步长δmin(t)应为一个很小的值。此外，随着迭代次数的增加，xmin(t)应逐渐趋于最全局优解，相应地，其步长δmin(t)也应逐渐趋于一个很小的值。同时，当迭代次数很大时，种群规模对于求解结果的影响较小。综合考虑这些因素，提出采用如下表达式来确定δmin(t)的第k个分量δmin,k(t)：

式中，p为种群规模。经过大量实验发现，当其指数取2.5时效果最好。

由于种群规模最小为1，因此在任何一次迭代时，δmin,k(t)都小于，不存在变异后解超出约束范围的情况。此外，智能优化算法的求解精度和稳定程度会随着种群规模和迭代次数的增加而提高，但种群规模和迭代次数的增加会导致运算时间和规模的扩大，同时种群规模和迭代次数的不同取值也可能对优化结果造成较大影响。而在式（4）的机制下，δmin,k(t)会随着种群规模和迭代次数的增加而减小，这将制约种群规模和迭代次数增加对优化结果的正面影响，进而减小种群规模和迭代次数的不同取值对优化结果造成的影响。

而对于第t次迭代时的第i个解xi(t)，它的步长δi(t)应位于区间[δmax(t),δmin(t)]内，并且它对应的适应度fi(t)越大，δi(t)就应该越大。鉴于此，本文采用指数形式来描述δi,k(t)和fi(t)的关系，即有：

式中，δi,k(t)为步长δi(t)的第k个分量，ai,k(t)和bi,k(t)分别为相应的系数。当xi,k(t)在区间内时取-，反之取+。结合式（3）与（4），可得到：

解得ai,k(t)和bi,k(t)分别为：

在以上提出的步长动态调整机制下，在算法运行的初期，迭代次数较小时，由于各解对应的适应度差值较大，根据式（5）和式（7）可知，此时算法的步长较大，算法的全局搜索能力较强，收敛速度较快。而到了算法运行的后期，大多数解对应的适应度会趋近最小适应度，根据式（5）和式（7）可知，此时步长δi,k(t)会趋近式（4）。由于该式的分母中存在t+p2.5，在算法运行后期迭代次数t很大时，搜索步长δi,k(t)会急剧减小，导致算法的全局搜索能力和收敛速度下降，甚至还可能使算法陷入局部最优。为解决这个问题，本文在算法运行前期使用式（5）来控制步长，在算法运行后期引入一种不考虑种群规模和迭代次数的自适应机制来控制步长，其基本原理如式（8）和式（9）所示：

式中，为第二种自适应机制下第t次迭代时第i个解的步长参数分别为第二种自适应机制下步长参数的最大值和最小值，为第二种自适应机制下的步长，xi,k(t)是第t次迭代时第i个解的第k个分量，‖xi(t)-xmin(t)‖为xi(t)与xmin(t)之间的距离，dmax(t)为最优解和其他解距离的最大值。

当解越接近最优解时，其‖xi(t)-xmin(t)‖和(xi,k(t)-xmin,k(t))的值越小，由式（8）和式（9）可知，其搜索步长也越小，有利于在最优解附近局部寻优；反之，当个体距离最优位置越远时，其‖xi(t)-xmin(t)‖和(xi,k(t)-xmin,k(t))的值越大，相应搜索步长也越大，有利于差的解跳出当前的不利位置。因此该自适应机制可以提高算法的全局寻优和局部寻优能力。此外，式（9）还通过引入Lévy飞行避免使算法陷入局部最优。

将上述两种步长动态调整策略相结合，可使算法在避免陷入局部最优的同时获得较快的收敛速度和较高的搜索精度。结合后的步长动态调整机制为：

式中，T为转折代数，大量实验的结果表明，T取50～150之间的值时优化效果最佳。

3.2 发现概率的动态调整机制

本文采用文献[16]所提出的自适应机制来描述发现概率，如式（11）所示：

式中，pa,i(t)为第t次迭代时第i个解的发现概率，pa,max和pa,min分别为发现概率的最大值和最小值。当某个解对应的适应度接近最小适应度时，其发现概率接近最小值，说明它不容易被抛弃；反之，当个体的适应度与最小适应度相差很大时，其发现概率接近最大值，说明它容易被抛弃。这有利于好的解被留下而坏的解被替换，从而可以加速算法的收敛速度。

3.3 参数动态调整的自适应布谷鸟算法

参数动态调整的自适应布谷鸟算法流程图如图2所示。

图2 参数动态调整的自适应布谷鸟算法流程图

相应的伪代码为：

1.Initialize a population withnsolutionsxi( 1),i=1,2,…,n

2.For all solutions do

3.Calculate fitness value byFi(1)=f(xi(1))

4.End for

5.While iteration numbert＜max iteration number

6.Calculate mutation step size by formula（10）

7.Generate new solutions according to mutation step size

8.Calculate fitness values of new solutions by

11.End if

12.Calculate discovery rate by formula（11）

13.Abandon some solutions according to discovery rate and generate new solutions to replace them by formula（2）

14.Calculate the fitness values of all solutions and pick out the best solution

15.Iteration numbert=t+1

16.End while

4 数值仿真与分析

4.1 仿真实验设计

为验证所提出的自适应布谷鸟算法的有效性，本文选取表1所示的10个标准测试函数进行仿真分析，并对比常规布谷鸟算法（以下记为CS）、文献[12]、[13]、[15]、[16]提出的改进的布谷鸟算法（以下分别记为ICS1、ICS2、ICS3 和ICS4）、粒子群算法（以下记为PSO）以及本文提出的参数动态调整的自适应布谷鸟算法（以下记为ACS）的测试结果。各算法的参数设置分别如表2和表3所示。其中，ACS的最优参数设置通过大量实验获得，其余各算法分别依照文献[12]、[13]、[15]、[16]设置参数。实验的测试平台为Matlab™环境，所用计算机硬件配置为（Intel®Core™i5-5200U）2.2 GHz，内存为4 GB。

表1 测试函数

表2 各种布谷鸟算法参数设置

表3 粒子群算法参数设置

4.2 实验结果及分析

针对不同测试函数，各算法独立运行100 次，得到的实验结果如表4 所示。其中，f1为单峰函数，但由于它在全局最小值附近函数值变化极为缓慢，因此常被用于评价算法的后期搜索性能。从100 次实验结果的最大值、最小值、平均值以及达到目标值的次数可以看出，ACS 的求解精度较 CS、ICS 以及 PSO 有大幅提高。同时，ACS 求解结果的方差远远小于其余算法，说明ACS的求解结果更加稳定。f2是一个复杂的多峰函数，拥有无数的局部极小值和局部最大值，常导致算法在求解时陷入局部最优。可以看到，虽然ACS 的求解精度和稳定性远远高于其他算法，但在求解后期却陷入了局部最优值4.44E−15。f3是典型的非线性多模态函数，搜索空间大并拥有许多局部极小点，通常被认为是智能优化算法很难求解的复杂问题。虽然从100 次实验结果的平均值和最大值来看，ACS的求解精度只是略微优于其他算法，但ACS达到目标值1E−05的次数更多，并且能够在其余算法的最好求解结果达不到1E−05 时搜索到全局最优解0，这说明ACS 的求解能力高于其余算法。与此类似，同样f4也是一个典型的非线性多模态函数。它的局部极小值的个数与问题的维数成正比，且函数峰谷起伏不定，因此也很难求解出全局最优值。可以看到，虽然ACS的100次实验结果均值和方差都与其他算法的结果相差不大，但ACS 可以搜索到全局最优解0，并且有更大的概率达到目标值。f5的全局最小值位于一个抛物线形的山谷中，由于山谷内函数值变化很小，很难求解出全局最优值，常被用于评价算法的搜索能力。可以看出，ACS在求解这个问题时的求解精度和稳定性都远远高于其余算法，说明ACS 的搜索能力很强。f6是一个复杂的二维函数，拥有无数个局部极小值并具有强烈振荡的特征，是评价算法收敛性和搜索能力的经典函数。可以从100次实验结果的最大值看出，ICS1、ICS2、ICS3、ICS4 以及 PSO 均在求解时陷入了局部最优值9.71E−03，而ACS 则避开了该值。同时，ACS可以搜索到全局最优值0，并且求解结果的最大值、平均值、方差以及达到目标值的次数均远远超过了其他算法。说明ACS 具有很强的收敛性和搜索能力。f7、f8和f9均为复杂多峰值函数，拥有许多局部极小值点。可以看到，ACS 的求解结果的最值、平均值以及稳定性均优于其他算法，并且ACS 大多数时候总能达到目标值。f10为一单峰函数，常被用于检测算法的寻优能力。可以看到，ACS的求解精度和稳定性均远远优于其他算法，说明ACS的寻优能力很强。

表4 多种算法的计算结果

各算法求解10 个标准函数的收敛曲线分别如图3至图12所示。可以看到，在求解初期，多数时候ACS的收敛速度虽然小于PSO 的，但大于其余算法。而PSO到了求解后期会陷入局部最优，ACS 除去在求解f2时陷入了局部最优，其余情况下都能在求解后期依然保持很快的收敛速度。

图3 f1 的收敛曲线

图4 f2 的收敛曲线

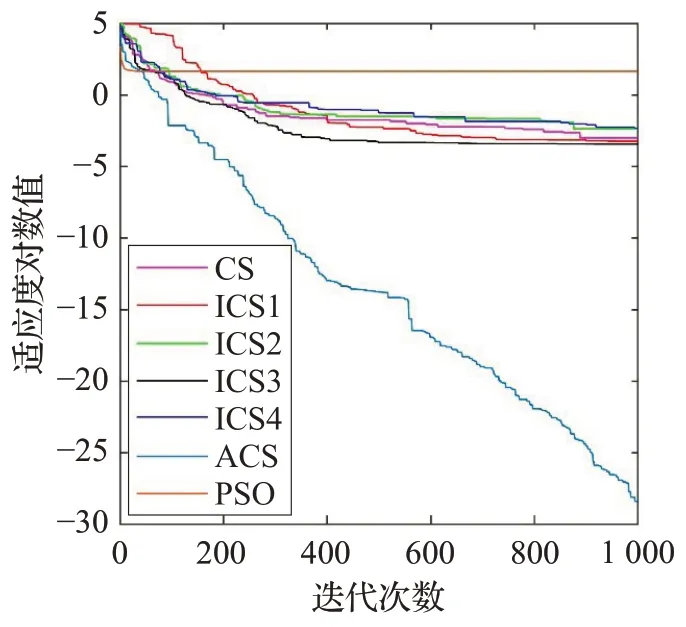
图5 f3 的收敛曲线

图6 f4 的收敛曲线

图7 f5 的收敛曲线

图8 f6 的收敛曲线

图9 f7 的收敛曲线

图10 f8 的收敛曲线

图11 f9 的收敛曲线

图12 f10 的收敛曲线

CS和ACS求解各函数所需的时间如表4中平均运行时间所示。可以看到，CS 与ACS 求解各函数的运行时间都很短，说明两种算法的运行速度均很快。此外，ACS求解各问题所需的时间略大于CS的求解时间。这是由于ACS 在CS 的基础上增加了自适应机制，使得ACS 的计算复杂度有一定的提高，导致ACS 求解优化问题所需的时间有所变长。需要说明的是，本文所提出的自适应机制仅需简单的代数运算即可实现，不会对算法造成很大的运算负担。

综上所述，相较于其他各算法，ACS 具有更高的计算精度和稳定性，收敛速度更快，不易陷入局部最优。此外，所提出的自适应机制在一定程度上没有给ACS增加运算负担。

5 结束语

本文简述了布谷鸟算法的基本原理。在前人研究基础上，本文提出了一种基于参数动态调整机制的自适应布谷鸟算法。所提出算法会依据解的好坏动态改变发现概率的大小，并在运算前期和后期分别利用两种自适应机制控制步长动态变化。通过对比该算法与其他算法求解10 个标准测试函数的结果，可知本文所提算法计算复杂性较低，并且在计算精度、稳定性以及收敛速度上均具有一定的优势。