高速磁浮组合式轨道梁的温度变形
莫然 滕念管
(上海交通大学船舶海洋与建筑工程学院,上海 200240)
磁浮交通是一种潜力巨大、高速节能、舒适安全的轨道交通方式,相比于轮轨系统,磁浮列车通过非接触的电磁悬浮力作用在轨道梁上,能以更快的速度运行。磁浮系统轨道梁的造价占磁浮系统总造价的60%~80%[1],研究磁浮轨道梁对于工程成本的控制至关重要。传统磁浮轨道梁由功能件与混凝土梁通过预埋件进行连接,其整体需在工厂内恒温环境下制作,工作量巨大且带来了一系列运输吊装的问题。而组合式轨道梁由承重梁与轨道板组成,重量大的承重梁在现场按常规精度制作,上部轨道板在工厂连同功能件在恒温环境下精确加工。该梁型大大简化了轨道梁的制作工艺以及对加工设备、场地、运输的要求,节省了建设投资的同时也加快了施工进度,拟在新一代高速磁浮交通中采用。
近年来,国内外对混凝土梁的日照温度效应做了大量研究。李全林[2]将太阳辐射分为太阳直射、太阳散射和地面反射3种方式,并考虑翼缘的遮挡作用,分别用平面梁模型和空间模型计算了箱梁温度应力,采用最小二乘法进行了曲线拟合。Taysi 等[3]通过试验对三维箱梁模型温度场的合理性进行了验证,并研究了影响箱梁温度分布的因素。朱小进[4]研究了在周围遮蔽物的影响下,混凝土表面水平向与垂直向受太阳辐射强度和太阳辐射通量的变化规律,发现太阳辐射的遮蔽作用仅对混凝土板的浅表层有明显作用。陈贤俊[5]等考虑太阳辐射、长波辐射、对流换热、风速等因素,建立桥墩三维瞬态日照温度场有限元数值仿真模型,有限元分析结果与实测数据吻合,验证了温度场有限元数值分析的准确性和实用性。王祥[6]采用双塔叠合梁斜拉桥的有限元模型,研究了在施工过程中各种温差环境对主梁挠度的影响。孙国晨等[7]利用ANSYS 有限元软件对实桥钢-混凝土叠合梁截面在日照作用下的温度分布进行时程仿真计算,评价了不同材质在叠合梁截面中的热力学性能。
磁浮轨道梁对温度极为敏感,而日照温差是造成轨道梁变形的主要原因之一。以往的研究多侧重于二维热分析,且组合式轨道梁的结构形式不同于其他等截面结构,现有规范无法对其进行温度变形分析。本文建立组合式轨道梁热-结构耦合有限元三维空间模型,研究连接构件对其温度场及温度变形的影响。
1 组合式轨道梁模型
组合式轨道梁(以下简称组合式梁)由下部的承重梁与上部的钢筋混凝土预制轨道板经连接构件整体浇筑而成,见图1。承重梁采用简支结构,轨道板中间部分预留定位开孔后运输至现场,承重梁顶部设置可伸入轨道板开孔的预设钢筋。承重梁与轨道板精确定位后,浇筑混凝土于轨道板的开孔内形成刚性连接。
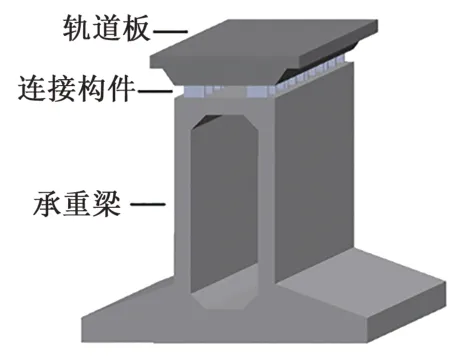
图1 组合式梁模型
承重梁跨度为24.768 m,每一跨上部混凝土预制轨道板分为4块,每块轨道板长6.192 m。承重梁梁高2.9 m,左右腹板厚0.2 m,组合式梁截面见图2。该尺寸下组合式梁在静荷载下的变形、一阶频率均符合磁浮轨道梁的要求,连接构件的抗弯、抗剪承载力均符合要求。功能件与轨道板在工厂组装完成,其对刚度影响较小,但是在日照情况下对梁的遮挡作用比较明显,因此建模中未考虑其刚度贡献,只考虑对太阳辐射的遮挡作用。每一块轨道板留有2×3排列的定位开孔,连接构件与上下梁整体浇筑后每一跨共有24个连接构件,其截面尺寸为0.2 m(长)×0.3 m(宽)。
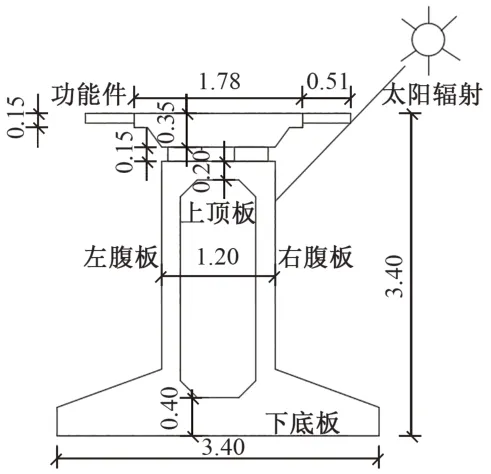
图2 组合式梁截面(单位:m)
2 温度场数值模拟
2.1 有限元模型
采用ANSYS 建立组合式梁有限元模型。由于连接构件的厚度与梁跨长相差较大,且梁为变截面梁,对连接构件及其附近采取网格加密处理,梁端铰接,取1跨梁为计算单位。温度场计算时采用solid70实体模型进行瞬态热分析,后续处理中可转换网格类型计算结构温度变形。混凝土的质量密度ρ为2 400 kg/m3,导热系数λ与比热容c分别为1.758 W(/m·℃)和916.7 J(/kg·℃)[8]。
2.2 热传导理论及边界条件
组合式梁的下部承重梁可视为没有上顶板的箱梁,且属于变截面梁,温度场分布较为复杂,是三维不稳定的热传导问题。其温度T与时刻t、空间坐标有关[9],表达式为

假定组合式梁为均匀、连续且各向同性的结构,连接构件与上下梁呈刚性连接。根据Fourier 热传导理论,热传导方程为

在日照环境下轨道梁温度场的计算中,如果没有轨道梁的实际温度,一般取当天的平均温度或上午6:00太阳未升起时的气温作为初始值[10]。本文取后者作为温度的初始值。
组合式梁在日照环境下受太阳辐射、对流换热的影响。根据介质与其周围介质热交换相互作用的特点,太阳辐射属于第二类边界条件,即
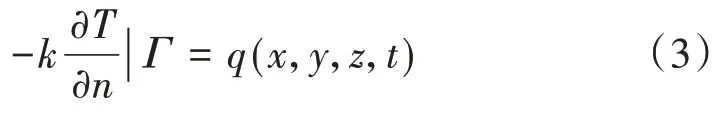
对流换热属于第三类边界条件,即
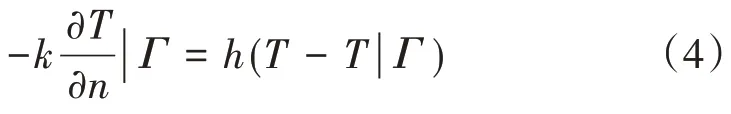
组合式梁所处热交换环境的边界条件为
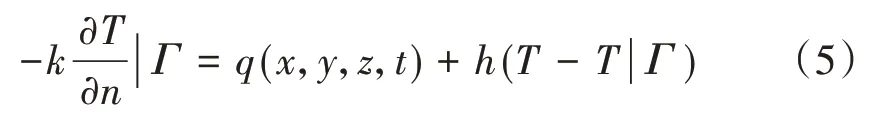
式中:k为导热系数,k=λ/(ρc);q为太阳辐射热流密度;h为考虑对流与辐射的综合换热系数;T|Г为结构初始温度;n为表面竖向矢量方向。
2.3 边界条件的处理及计算
假定组合式梁的走向为南北向,太阳轨迹与其垂直时太阳辐射对梁的影响最大[10];假定轨道梁附近没有任何遮挡。太阳辐射qs包括太阳直射、太阳散射和地面反射。太阳辐射量与太阳常数、太阳赤纬、太阳时角、轨道梁走向有关[11]。太阳赤纬与太阳时角共同决定了太阳的入射角、高度角及方位角,倾斜度不同,受太阳直射的影响不同。此外,梁各表面的位置不同,受地面反射及太阳散射的影响也不同,因此各表面须单独计算。由于600 km/h 磁浮试验线将在青岛建设,本文选取青岛7 月23 日的太阳赤纬,根据文献[11]的方法计算得到组合式梁各表面的太阳辐射量,见表1。
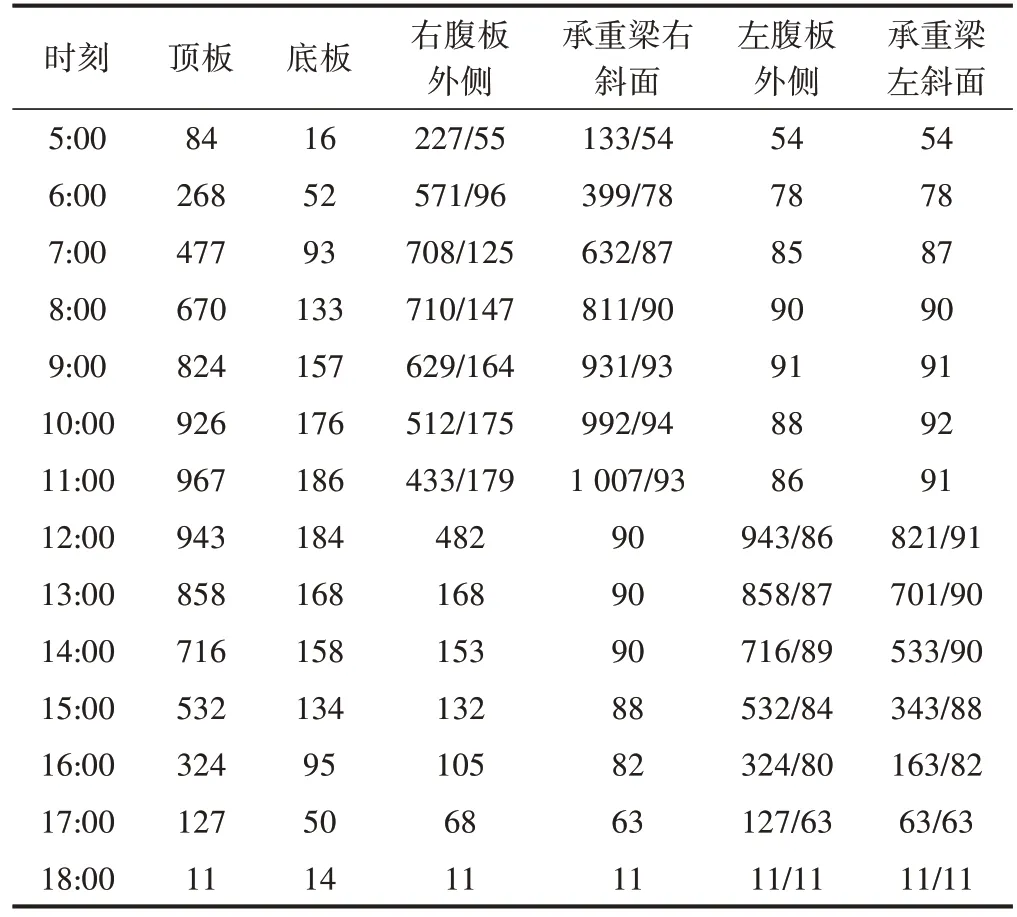
表1 太阳辐射量 W·m-2
查询近10 年青岛的天气情况,可知2017 年7 月23 日最高气温为33 ℃,最低气温为28 ℃。一天中气温随时间正常变化的规律符合正弦函数曲线,即
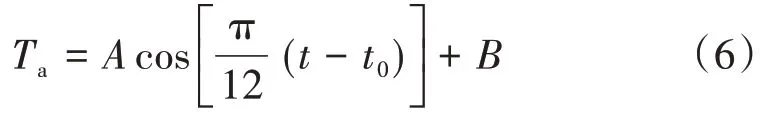
式中:t0为出现最高气温的时刻;Ta为t时刻的大气温度;A和B为待定系数。
一般最高气温出现在14:00左右,结合式(6)绘制青岛的气温变化曲线,如图3所示。
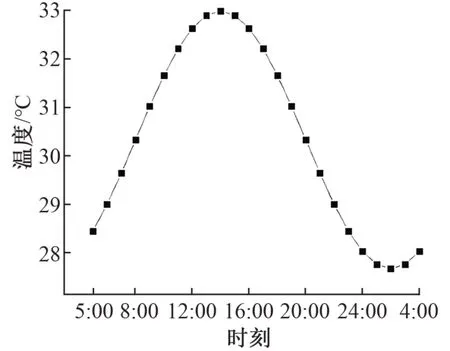
图3 日温度变化曲线
对流换热系数主要取决于风速、表面方位、材料属性等,其中风速的影响最大。对于组合式梁而言,对流换热系数hc[8]可以表示为
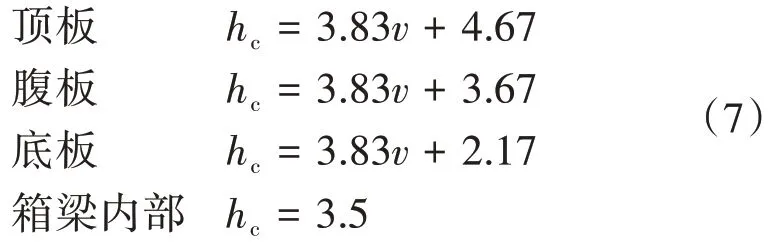
式中:v为风速,查询可知青岛7 月以3 级风为主,故v=3.5 m/s。
长波热辐射换热是指物体与介质之间通过长波辐射进行热量交换,其系数hr[8]可表示为
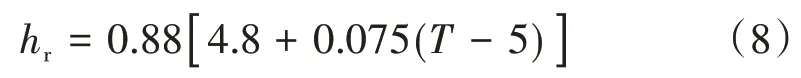
在自然条件下,长波热辐射换热系数差别不大,夏季取T=30 ℃。根据上述参数计算得到组合式梁各表面综合换热系数,见图4。
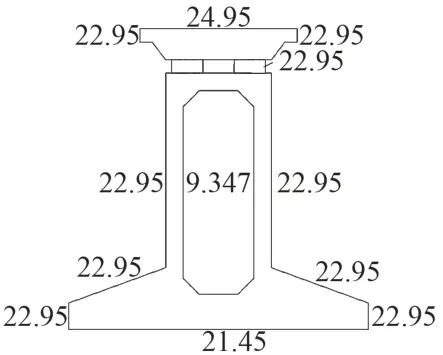
图4 组合式梁各表面综合换热系数
3 组合式梁计算结果分析
3.1 不同时刻组合式梁温度场云图
利用ANSYS对组合式梁进行三维瞬态热分析,得到其一天之内的温度分布变化情况,如图5 所示。可知,随着太阳入射角的变化,组合式梁各个部位的温度开始发生变化。右腹板温度率先升高,带动箱梁内部温度增加,随后左腹板温度升高,右腹板的温度逐渐降低。受太阳直射的表面温度上升较快,温度较高;没有太阳直射后,温度迅速下降。梁体内部的温度变化则较为缓慢,存在一定的滞后性。
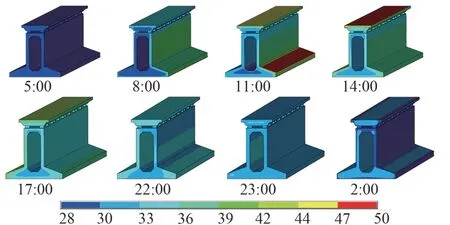
图5 组合式梁温度场分布(单位:℃)
3.2 组合式梁变截面节点温度对比
为探求组合式梁的温度场特性,在适当位置选取轨道板横向节点(N1—N5)、右腹板竖向节点(N6—N11)以及承重梁底板横向节点(N12—N17)(图6),绘制温度时程曲线(图7)。其中,N1—N5 节点距轨道板左侧分别为0,0.45,0.89,1.34,1.78 m;N12—N16 节点距底板左翼缘分别为0,0.85,1.70,2.55,3.40 m。
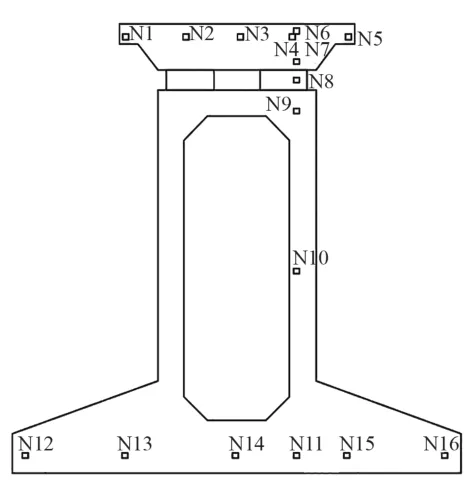
图6 截面节点布置情况
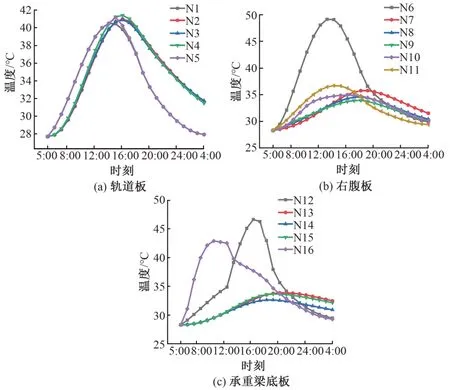
图7 轨道板、右腹板及承重梁底板温度时程曲线
由图7(a)可知,N1,N5 节点温度上升和下降都快于内部各节点。原因是轨道板两侧直接与空气接触,受空气温度影响较大;内部混凝土温度上升后,散热较慢,15:00 后温度大于轨道板两侧温度,出现外冷内热的情况,最大温差也出现在此时段。
由图7(b)可知:N6 节点温度上升较为迅速,且变化较大,差值达到了20 ℃;N11 节点受地面反射和太阳散射的影响,温度也较高;由于轨道板厚度较小,N7节点的温度大于其余右腹板内部节点温度;其他节点温度变化较为平缓,且存在一定的滞后性。
由图7(c)可知:N16 节点受阳光照射温度迅速上升,随后照射角度变小温度趋于稳定,下午开始下降;在下午太阳照射后N12 节点温度迅速升高;中间位置的节点温度变化较为缓慢。
对比图7(a)与图7(c)可知,轨道板内部与表面温度差别不大,而承重梁底板内部温度则显著低于其表面温度。原因是轨道板内部受上下2个方向热传导的影响,温度传递速度高于承重梁底板内部,使得其温度变化、极值均大于承重梁底板内部。
选取梁跨中位置附近有连接构件的截面1和无连接构件的截面2,根据温差最大值所在时刻分别提取22:00,16:00 时的数据绘制轨道板及承重梁底板横向温度变化曲线,见图8。可知,2 个截面的温度变化曲线大致相同,说明连接构件存在与否对梁横向温度分布没有影响。
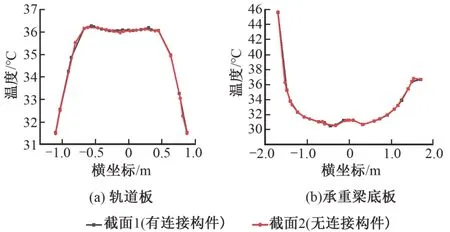
图8 轨道板及承重梁底板横向温度变化曲线
14:00 右腹板竖向温度变化曲线见图9。可知,2个截面的右腹板随温度的变化基本一致,在轨道板的上部以及承重梁下部的大部分区域内温度变化完全一致,而在连接构件附近温度分布不同,截面1 与截面2最大温度差达到了1.2 ℃。由于承重梁下部混凝土较厚,距底面0.25 m处的混凝土温度远低于其他部位。
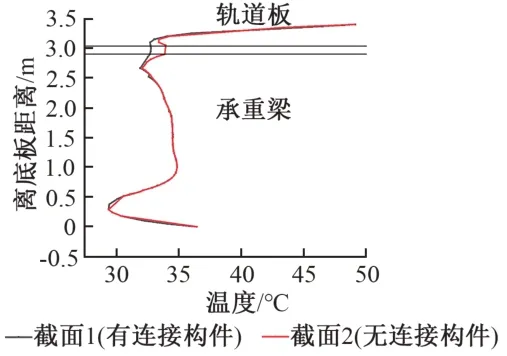
图9 右腹板竖向温度变化曲线
4 连接构件对组合式梁温度变形的影响
4.1 连接构件的形式
建立2个梁模型研究连接构件所处的间隔段对组合式梁温度场及温度变形的影响:①假设连接构件填满了间隔,形成整梁(图10(a));②取消连接构件形成无连接构件梁,即连接构件刚度为0(图10(b))。在相同的日照环境下研究连接构件对温度场的影响。

图10 整梁及无连接梁模型
由于承重梁底板离连接构件较远,因此选取轨道板横向节点及右腹板竖向节点对比组合式梁、整梁及无连接梁的温度场。22:00 时轨道板横向温度变化见图11(a),14:00时右腹板竖向温度变化见图11(b)。

图11 轨道板及右腹板温度变化曲线
由图11(a)可知,整梁截面中间节点的温度显著低于其他截面,原因是轨道板可以从2 个方向与外界迅速进行热交换,使其内部温度大于整梁的内部温度。
由图 11(b)可知,3 类梁所选4 种截面的温度曲线较为相似,而在连接构件间隔处温度稍有差异。截面2和无连接构件梁在连接构件处温度最大,截面1次之,整梁连接构件处温度最低。整梁比组合式梁在连接构件处的温度低约3 ℃,截面变化对连接构件处的温度场影响较大,对于无连接梁截面的影响较小。
组合式梁和整梁在14:00时的竖向最不利温度变形云图和16:00时的横向最不利温度变形云图分别见图12和图13。可知,组合式和整梁的竖向最不利温度变形均出现在梁中间位置,而横向最不利温度变形则出现在梁端位置。
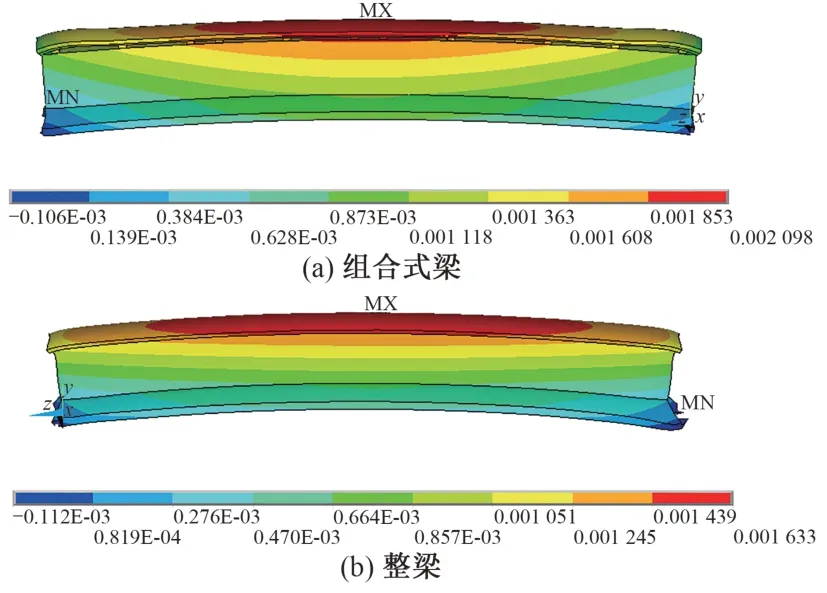
图12 竖向最不利温度变形云图(单位:mm)
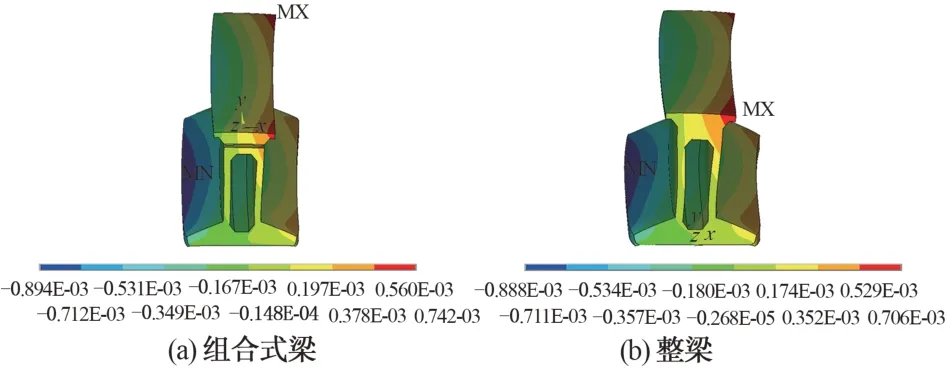
图13 横向最不利温度变形云图(单位:mm)
根据《高速磁浮交通设计规范》(征求意见稿)可知,单跨简支磁浮梁在日照条件下引起的竖向变形应小于L/6 500,引起的横向变形应小于L/5 800,其中,L为梁跨。对于本文组合式梁,竖向和横向温度变形限值分别为3.84,4.31 mm。组合式梁与整梁的最不利温度变形对比见表2。
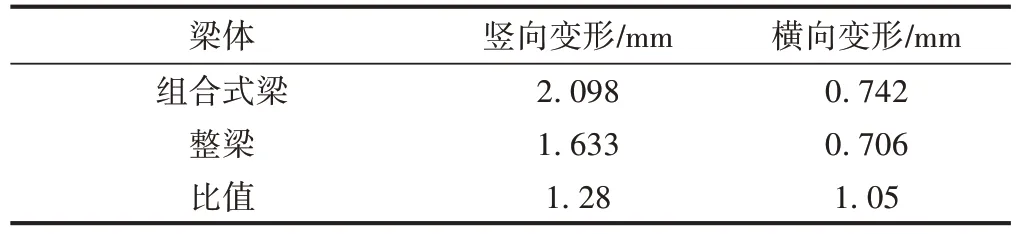
表2 组合式梁与整梁最不利温度变形对比
由表2 可知,组合式梁与整梁的竖向及横向变形均符合规范要求,组合式梁的竖向温度变形明显大于整梁,横向温度变形虽大于整梁但幅度小。这说明在温度场作用下,组合式梁截面变化对竖向变形的影响大于横向变形。
4.2 连接构件的高度
轨道板与承重梁之间的连接构件会影响组合式梁的温度场与刚度,进而影响组合式梁的温度变形。保持连接构件与轨道板及承重梁的接触面积不变,研究连接构件高度H不同时梁体的最不利温度变形,见表3。可知:当H=0,即梁为整梁时,竖向变形与横向变形较小;当梁为组合式梁时,随着连接构件高度的增加,竖向和横向变形变化不显著;H= 150 mm 的组合式梁与整梁相比,竖向变形增加了约16%,横向变形增加了约7%。这说明连接构件的高度对竖向和横向最不利温度变形影响较小。
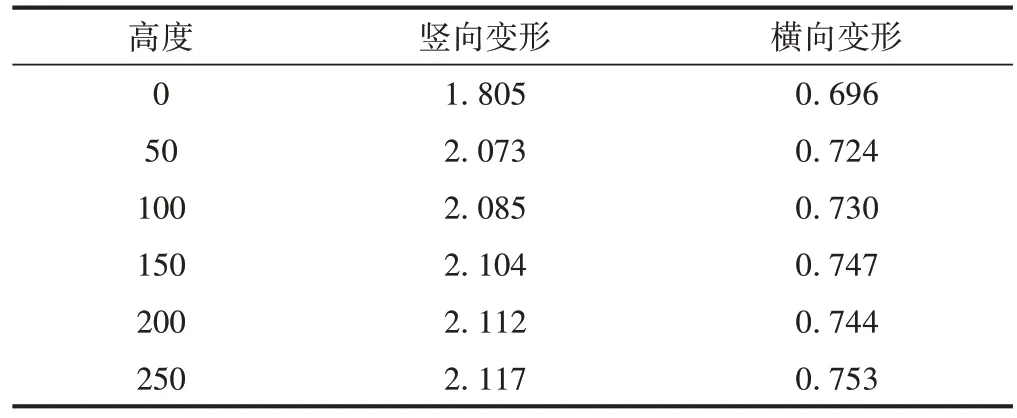
表3 连接构件高度不同时梁体的最不利温度变形 mm
5 结论
1)组合式轨道梁的轨道板与承重梁通过二次浇筑的连接构件进行连接,不同截面的温度场不同。
2)轨道板及承重梁中部到底部的竖向温度分布较为一致,受截面变化影响较小。
3)有连接构件的截面温度场受截面变化影响,与相同尺寸整梁的温度场不同。截面变化对轨道板及连接构件梁的温度场影响较大,对无连接构件梁的温度场影响较小。
4)在日照温差作用下,组合式梁截面变化对竖向变形的影响较大,对横向变形影响较小。连接构件的高度对竖向和横向最不利温度变形影响较小。

