基于可靠度的桥梁全寿命设计方法

王崇交 李亚东

（西南交通大学土木工程学院，成都 610031）

传统的桥梁设计方法仅考虑桥梁的初期性能和初始建造成本，采用定值设计方法来满足设计规范条件下的参数最低要求，常常发生严重的桥梁使用问题并造成巨大的经济损失。根据美国联邦高速公路管理局统计，美国高速公路桥梁由于耐久性不足，2002年直接运营成本超过83 亿美元，由此产生的交通延误、生产力损失等间接成本可达其10 倍［1］。因此，为了提高公共安全与交通舒适度，降低使用期内的运营养修成本，采用考虑桥梁长期使用性能的全寿命设计方法至关重要。既往研究中常采用单目标优化的形式，通过最小化各种失效概率或最小化确定性约束条件下的预期总成本来对桥梁设计方案进行优化，由于可参与优化的设计目标数量十分有限，无法有效满足各方面的工程要求。因此，需要研究与规范结合且涵盖多个设计目标的桥梁全寿命设计方法。

国内外学者针对桥梁结构全寿命设计已开展了一些研究。文献［2］对全寿命设计方法的基本思路、理论方法、设计过程进行了研究，认为全寿命设计方法具有均衡结构耐久能力、延长使用寿命、减小全寿命成本的优点，可在结构设计的初步设计阶段发挥作用。文献［3］提出了一种基于可靠度的多目标设计优化方案，用于考虑腐蚀影响的钢筋混凝土桥梁全寿命设计。文献［4］以可持续发展为目标提出了结构综合全寿命设计法，旨在优化人类生存状态、减小工程的经济成本和环境影响。文献［5］将桥梁全寿命期内不同时期发生的费用折算为现值并加以比较，提出了净现值计算模型，直观反映分析期内建设、维修、更换等各项费用的影响程度。文献［6］将桥梁对环境造成的当前影响和未来影响分别进行了评估，按各影响类别对整体环境效应的相对重要性加权，计算加权平均影响评分作为全寿命环境评估的依据。

现有的桥梁全寿命优化设计方法仍存在以下不足之处：①使用确定性方法时主要依赖桥梁所在区域的统计资料和工程师的经验，未考虑使用过程中的不确定性，从而影响方案比选的准确性和经济性。②通常涉及多个函数的计算，且计算参数多为随机变量，计算量大，计算结果的精度难以保证。③全寿命优化过程中各个优化目标之间界限模糊，优化设计内容存在重复或遗漏。④无法体现桥梁在自然因素作用下的持续劣化，特别是人为因素影响下桥梁性能上升下降的动态变化过程。

本文提出了一种基于可靠度的桥梁全寿命设计方法，旨在通过考虑桥梁从建设到拆除的整个使用周期内荷载、环境和各类灾害的作用以及工程活动对桥梁周围的自然环境、社会经济造成的影响，制定出合理的设计方案、养修管理方案、灾害应对方案，使桥梁结构在全寿命周期内性能均能满足预期目标且具有良好的经济效益。其基本思路是：采用时变可靠度的方法分析结构性能的动态变化，利用桥梁结构时变可靠指标和时变状态指标结合成本效益最优目标，将桥梁全寿命设计与规范规定的设计目标、建设者期望的经济效益目标相结合。

1 桥梁全寿命可靠度设计

桥梁的可靠性指结构在设计使用寿命内达到预定使用要求的概率，用可靠度β和失效概率Pf来度量，一般采用功能函数的形式进行计算，即

式中：Z为极限状态功能函数；R为广义结构抗力；S为广义结构效应。

结构可靠度β和失效概率Pf分别表示为

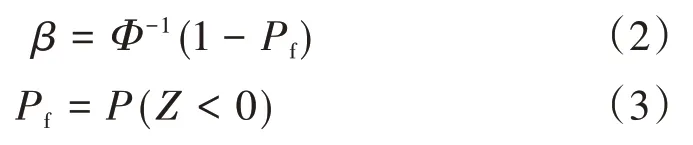
1.1 桥梁安全性设计目标

桥梁的安全性包括桥梁使用者的生命财产安全和结构自身在使用过程中的安全，对应承载能力极限状态，如结构或构件失去平衡、发生断裂等。能够安全地承受各项设计荷载是对桥梁结构的基本要求。对于承受循环荷载的结构，需要考虑构件的疲劳寿命和疲劳极限，对损伤后需要快速修复的重要桥梁结构，可恢复性也是一项重要的安全性指标［7］。根据中外桥梁实际使用寿命和桥梁事故的统计结果［8］，按我国现有标准设计的桥梁结构在到达设计使用寿命之前，其承载能力通常已低于规范要求，结构的使用寿命往往达不到设计要求。全寿命设计中使用的承载能力可靠度应随时间变化，且要求桥梁的承载能力在整个寿命期内均能满足规范要求。

在使用过程中，桥梁性能会受到诸多因素的共同影响，且劣化后结构性能表现出非线性化，因此需要更合理的劣化模型。本文采用彭建新［9］提出的非线性劣化的指数模型表征全寿命周期内承载能力极限状态的可靠度βB（t），即

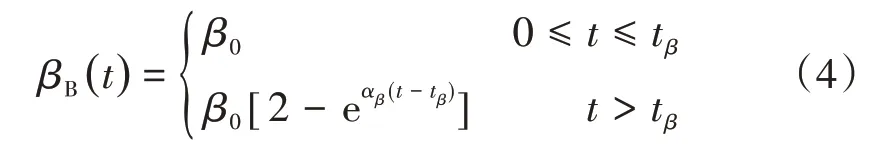
式中：t为结构实际使用年限；β0为结构初始可靠度；tβ为结构开始劣化时间；αβ为可靠指标劣化率。

总体上，桥梁结构安全性设计要求保证结构在全寿命周期内承载能力极限状态的可靠度βB（t）大于规范规定的目标可靠度βT，即βB（t）＞βT。

各国规范对桥梁结构的目标可靠度要求不同。针对承载能力极限状态，欧洲规范BS EN 1990 将桥梁结构划分为3个安全等级，并根据不同的设计基准期规定了不同的目标可靠度，见表1。美国规范AASHTO LRFDUS—2017依据桥梁结构的重要性给出了建议的目标可靠度，见表2。我国规范GB/T 50289—1999《公路工程结构可靠度设计统一标准》根据结构重要性和破坏形式规定了不同的目标可靠度，见表3。

表1 桥梁结构承载能力极限状态的目标可靠度（欧洲规范）

表2 桥梁结构承载能力极限状态的目标可靠度（美国规范）

表3 桥梁结构承载能力极限状态的目标可靠度（中国规范）

桥梁结构目标可靠度的最优化设计与当地的经济、技术实力有关。将表1—表3中不同设计基准期下的目标可靠度换算到相同设计基准期下，发现我国规范的目标可靠度显著高于欧美规范。这是由于我国正处于经济的快速增长期，社会发展日新月异，需要在工程设计时对未来可能面临的荷载快速增长留有更多的富余度。

1.2 桥梁适用性设计目标

桥梁的适用性对应的是结构或构件可能在满足承载能力的情况下出现不适合使用的情形，如出现使行人感到不舒适或限制结构功能有效性的变形或震动，产生影响外观、耐久性或结构功能的损坏等。通常在结构安全性设计的基础上，通过设定正常使用极限进行结构适用性设计。文献［10］用线性模型描述了这种使用过程中逐渐产生的变化。

为反映结构在使用过程中复杂的适用性变化，参考承载能力极限状态劣化模型，建立非线性模型表征全寿命周期内正常使用极限状态的可靠度βC（t），即

式中：C0为结构初始状态指标；tC为结构开始劣化时间；αC为状态指标劣化率。

总体上，桥梁结构适用性设计要求保证结构在全寿命周期内正常使用极限状态的可靠度βC（t）大于规范规定的目标可靠度βT，即βC（t）＞βT。

承载能力极限状态的可靠度βB（t）与正常使用极限状态的可靠度βC（t）之间既有联系又存在不同。在没有对桥梁进行养修时，二者相互独立。当考虑桥梁养修时，有的养修活动先对βC（t）产生影响，进而对βB（t）起作用，如裂缝灌浆改善了结构外观，延缓了结构开裂并降低了结构性能的退化速率；有的养修活动（如更换翻新）对βC（t）和βB（t）同时起作用。

各国规范对桥梁正常使用极限状态下的目标可靠度指标的规定都较为粗略。我国GB/T 50289—1999中只给出了正常使用极限状态目标可靠度的推荐值为0.5 ～1.5。欧洲规范BS EN 1990规定，设计基准期为1 年和50 年的正常使用（不可逆）极限状态的目标可靠度分别为2.9，1.5；设计基准期为50 年的疲劳极限状态的目标可靠度为1.5 ～3.8。显然，正常使用极限状态的目标可靠度要远低于承载能力极限状态的目标可靠度，这是为了在不涉及结构安全的领域给予设计师更多的发挥空间。

1.3 桥梁耐久性设计目标

为了更好地描述桥梁在全寿命周期内耐久性的变化，从实用性角度提出了与结构耐久性相关的2 阶段极限状态，并结合ISO 13823：2008 中关于结构耐久性设计的一般原则提出桥梁全寿命耐久性指标。

第1阶段耐久性极限状态描述结构开始劣化的耐久性初始极限状态，是针对结构使用过中表观状态的定义。如钢筋混凝土结构在碳化或氯离子扩散的影响下钢筋锈蚀并开始出现裂缝，或钢结构、木结构的表面防腐涂层失效导致其开始腐蚀，即认为其达到了耐久性初始极限状态，需要对桥梁进行修复。耐久性初始极限状态用公式表达为

式中：SE，lim为环境作用效应的临界值；SE为结构在环境作用下的响应；TS为结构实际使用寿命；Tstart为结构劣化起始时间。

第2阶段耐久性极限状态描述桥梁结构实际使用性能的耐久性最终极限状态，是基于结构使用功能的定义。如钢筋混凝土结构由于钢筋锈蚀产生的裂缝宽度过大或保护层剥落导致钢筋外露，钢结构由于锈蚀而呈现令使用者难以接受的外观，即认为其达到了耐久性最终极限状态，需要进行构件更换或结构大修。耐久性最终极限状态用公式表达为

式中：ZD为耐久性极限状态功能函数；TD为结构设计使用期。

现行各国规范对桥梁耐久性极限状态的目标可靠度指标尚无明确规定。ISO 13823：2008 提出，结构耐久性极限状态的可靠度应基于结构和构件的设计使用寿命、结构的养修难度和养修成本、结构的失效后果等因素确定，并且酌情考虑专家意见和客户需求［11］。在全寿命耐久性设计中，还应考虑桥梁抗力和效应的时变特性。参考正常使用极限状态的设计方法，将全寿命耐久性设计的功能函数、失效概率、可靠度表达为

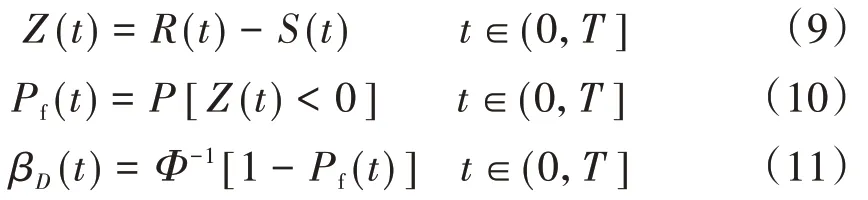
式中：Z（t）为结构在某一时刻的耐久性功能函数；R（t）为t时刻的广义抗力；S（t）为t时刻的广义作用效应；Pf（t）为t时刻结构失效概率；βD（t）为t时刻结构耐久性可靠度。

桥梁结构寿命周期各类耐久性指标的变化如图1所示，该图直观反映了各类指标之间的关系。其中Pt为结构目标失效概率，Pt=Pf（TD）。

图1 桥梁结构寿命周期耐久性指标的变化

2 桥梁全寿命经济性设计

全寿命经济性设计考虑桥梁从设计到拆除整个寿命周期的各项直接和间接成本，得出不同的桥梁设计方案在整个寿命周期的综合经济效益。

2.1 直接成本计算方法

直接成本指参与桥梁建造各方所投入的建设资金，可以分为桥梁建成前的建设成本C前和建成后的检测、维修、更换等后期运营需要的成本C后。

桥梁建成前的建设成本可表示为

式中：CD为设计成本；CC为初始建造成本。

CD为确定性成本，一般为初始建造成本的d%，即CD=CC·d%，在优化分析中可以忽略。CC由建设单位提供。

桥梁建成后的运营成本可表示为

式中：T为桥梁全寿命周期；Cins为检测成本；Crep为一般维修成本；Cm为大修或更换成本；Cr为拆除回收成本。

桥梁需要在一定的时间间隔内进行检测，以确保其实际性能满足使用要求。秦权［12］提出了与时间相关的计算方法，检测成本Cins的计算公式为

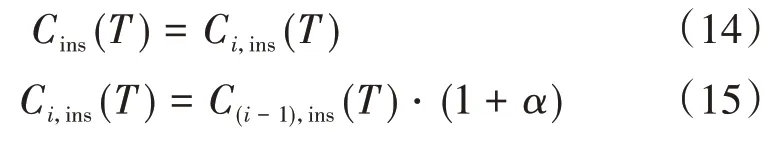
式中：K为全寿命周期检测总次数；Ci，ins（T）为第i次检测时的费用，本文假设桥梁每次检测费用与桥梁状态相关，检测费用逐次增加；α为比例常数，由桥梁的劣化状态确定。

对于相对复杂的维修成本计算，本文提出了基于耐久性极限状态的维修方式和成本计算方法。引用Bocchini 等［13］对维修活动的发生时间和时间间隔2 项设计参数的计算方法，将维修成本分为一般维修成本Crep和大修或更换成本Cm，计算公式为

式中：Crep，i为桥梁全寿命周期内的第i次一般维修成本；Pd1，i为桥梁第i次耐久性初始极限状态下的失效概率；Cm，j为桥梁全寿命周期内第j次大修或更换成本；Pd2，j为桥梁第j次耐久性最终极限状态下的失效概率；tPI，tP分别为初始维修时间和维修使用时间间隔。

Crep，i，Pd1，i，Cm，j，Pd2，j均为设计变量的隐函数，取决于桥梁建造时的设计与施工，如混凝土保护层厚度、钢结构涂装体系等。

2.2 间接成本计算方法

桥梁在全寿命周期的建造、维修等工程活动不仅需要资金投入，还消耗大量资源，造成环境污染及生态破坏，并且可能影响桥梁正常发挥运输功能，对桥梁所在地的区域交通造成不良影响。这类损失的货币价值称为间接成本。本文重点考虑桥梁全寿命期对周围环境及社会造成的影响。

2.2.1 社会成本

社会成本主要来源于桥梁养修时由于交通堵塞、延迟、线路改道等造成行车时间损失以及路况不佳可能引发的交通事故。桥梁交通状况的模拟较为复杂，美国联邦公路局（Federal Highway Administration，FHWA）开发的交通仿真软件TSIS 可对桥梁维修时的交通流情况进行模拟，确定维修过程中的交通耽搁时间、交通堵塞程度、车速等，进而计算出由于养修活动造成的社会成本。

桥梁维修造成的行车时间损失成本期望值CDDC的计算公式为

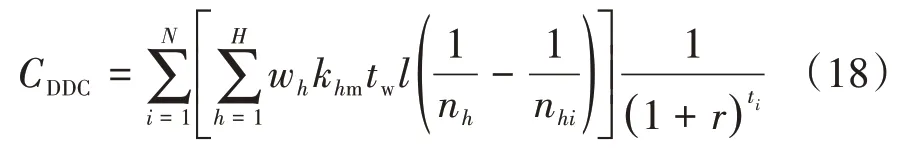
式中：N为维修总次数；H为车型种类（如货车、公交车、私家车等）的数量；wh为某一种车型的驾驶员时间成本；khm为某一类型车的交通量；tw为维修时交通延误时间；l为维修施工影响长度；nh为不维修时的正常运行车速；nhi为维修时某一种车型的车速；r为累积成本折现率；ti为第i次维修的发生时间。

桥梁维修时可能引发的交通事故损失成本期望值CACC的计算公式为

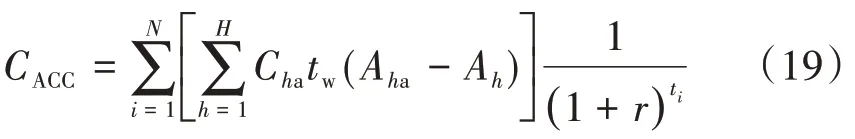
式中：Cha为某一车型发生事故的成本损失；Aha为某一车型在维修时的事故率；Ah为正常行驶的事故率。

2.2.2 环境成本

桥梁工程活动对环境的影响通常需要经历长时间的累积才得以体现，而生态环境在全寿命这个较长的时间跨度内也是一个易变的系统，因此桥梁的环境影响大多难以直接界定和量化。文献［14］提出了环境影响计算方法，主要考虑了全球变暖、水污染、空气污染3 种环境影响因素。每种影响因素对应1 个潜在影响指数，这些指数是由工程中各种物资的使用量（如混凝土用量、钢筋用量等）对环境影响的相对贡献加权得出的。各因素的潜在影响指数IAequ，jk的计算公式为

式中：IAj为不同类型的物资使用量；IVjk为不同类型物资的排放量；IVwjk为不同类型物资排放的权重；Nk为影响量的标准规格化值。

环境治理成本Cequ的计算公式为

式中：p为所考虑的环境影响物资类别数；IApoc为影响指数对应的污染治理成本。

对于计算中需要的污染治理成本等数据，美国环境保护局研究与发展办公室（US EPA Office of Research and Development）发布了环境影响标准化参数［15］。将每类环境影响除以固定的影响规模和治理成本，产生某一个影响类别的标准化参数，再将该参数置于所有促成该影响的工程活动中进行加权，得到环境影响标准化参数。

综上，全寿命期内发生的综合成本LCC（T）的表达式为

3 与既有桥梁全寿命设计方法的对比

3.1 体系组成

既有桥梁全寿命设计方法（简称既有方法）普遍存在设计概念模糊、设计指标重复或缺失等问题，缺少与现行规范的联系，在全寿命成本计算方面也缺少完整的计算体系。

本文提出的桥梁全寿命设计方法（简称本文方法）将设计目标明确分为基于可靠度的结构自身性能设计、基于成本形式的结构全寿命经济性设计。结构自身性能设计包括安全性、适用性、耐久性3 方面内容，均采用极限状态的形式来表达并与现行规范相结合。结构全寿命经济性设计包括桥梁从建设到拆除整个过程的资金投入、桥梁工程活动对环境和社会的相关影响，并在结构的设计和优化过程中转化为统一的成本形式来计算。

3.2 设计理念

既有方法按照传统土木工程的设计理念来划分设计目标和设计层次［16］，设计过程中普遍存在主观性，并且难以体现设计参数在寿命周期中随时间变化的特点。

本文方法关注了桥梁在全寿命过程中的长期性能，同时将结构成本、社会成本、环境成本组合成统一的动态成本计算形式，以方便桥梁结构全寿命的优化、设计和管理。

3.3 结构自身性能设计内容

既有方法采用固定不变的可靠度指标。本文方法将时间因素融入到全寿命设计方法的可靠度指标设计体系中，解决了既有方法中相关指标约定不明且与规范脱节的问题。

本文方法以时变可靠度理论为基础，采用极限状态设计方法来保证桥梁在全寿命期内的各项指标均能满足使用要求，以实现结构性能的动态设计。

本文方法将耐久性融入到全寿命设计中，基于工程实践提出了2 阶段耐久性极限状态，并采用时变可靠度来表达，突破了传统桥梁设计在耐久性部分的静态设计方法，反映了桥梁在长期使用过程性能的动态变化以及人为因素对其造成的影响。

3.4 经济性设计内容

既有方法在社会影响方面缺乏明确的计算方法，在环境影响方面仅停留在定义和评估层面，未完全确定相关环境影响指标。

新体系中基于交通仿真软件TSIS 和环境影响标准化参数的影响成本计算方法，将全寿命经济性设计进行了更详细的划分，为定性评价和定量分析提供了更完善的方法，使经济性计算结果更为全面可靠。

4 结语

本文提出的基于可靠度的桥梁全寿命设计方法更为直观地反映了结构性能与成本投入的对立统一关系，丰富了桥梁全寿命设计的内涵，使其更具有普适性，促进其在实际工程中的应用。

桥梁全寿命设计理念在实际桥梁工程中的应用并不算多，这是由于其较为繁琐的设计和计算过程，特别是对于桥梁结构的运营情况和性能状况需要采集大量的信息，这都要求较大的人力投入，目前还难以实现。随着信息技术革命以及5G 时代的到来，已经出现了诸如智慧城市、智慧园区等智能管理模式，智能化将是人类未来的发展趋势。笔者相信在不久的将来也会出现第一座“智慧桥梁”，而桥梁全寿命设计理念会成为她的灵魂。