动态异面压缩下铝蜂窝平均坍塌应力分析与试验验证

朱宇博,荣吉利,宋乾强,张 涛,吴志培

(1.北京理工大学宇航学院,北京 100081；2.北京宇航系统工程研究所,北京 100076；3.中国运载火箭技术研究院,北京 100076)

0 引 言

铝蜂窝材料具有相对密度低、质量轻、比刚度比强度高、缓冲吸能性能好、耐腐蚀耐老化、制造工艺成熟等特点[1-3]，常作为一种缓冲器材及防撞结构应用在航天器上吸收着陆冲击能量[4-7]。铝蜂窝优越的缓冲性能主要归功于其良好的异面压缩性能。

如图1所示，当沿着z轴方向压缩铝蜂窝时，称之为异面压缩；而在xy平面内压缩铝蜂窝时，称之为面内压缩。

图1 铝蜂窝异面示意图

在铝蜂窝异面压缩的理论研究方面，Wierzbicki[8]于1983年给出了单双壁规则(铝蜂窝单元的六个面中有四个面具有单倍壁厚、两个面具有双倍壁厚)，并提出了“超折叠单元理论”。Gibson等[9]在Wierzbicki的研究基础上，通过对六边形铝蜂窝的理论及试验研究后给出了六边形铝蜂窝受准静态异面压缩时的平均塑性坍塌应力计算公式

(1)

式中：σ0为铝蜂窝的屈服应力，t为铝蜂窝壁厚，l为铝蜂窝边长。式(1)为铝蜂窝异面压缩中平均塑性坍塌应力的经典计算公式，但是由于简化假设，使得理论应力值与实际应力值之间常常存在较大偏差(超过15%)。

荣吉利等[10]简化了超折叠单元理论，给出了两个准静态异面压缩下铝蜂窝平均塑性坍塌应力的理论计算公式，理论计算应力值与试验应力值相比误差较小(小于10%)。不过，由于在动态冲击中，材料具有应变率效应，荣吉利等的研究不适用于动态冲击工况。

而在铝蜂窝吸能装置的使用过程中，通常承受的是动态冲击载荷，所以研究动态冲击载荷下铝蜂窝的平均塑性坍塌应力具有很高的工程意义。罗昌杰等[11]基于蜂窝材料的对称性特点，根据能量守恒原理，推导了动态压缩下铝蜂窝的平均坍塌应力，不过与试验应力相对比，误差在-6.08%～12.04%之间，精度并不高。

本文在荣吉利等[10]研究的基础上，考虑铝蜂窝材料应变率效应对力学性能的影响，根据Cowper-Symonds模型，求取了应变率的表达式，推导了铝蜂窝动态平均塑性坍塌应力计算公式，并通过落锤冲击试验及仿真计算，验证了理论推导的正确性与有效性，本文提出的理论公式较前人研究成果具有更高的计算精度。

1 铝蜂窝异面压缩理论推导

铝蜂窝受异面载荷作用下典型的应力-应变曲线如图2所示，铝蜂窝变形依次经过弹性变形段、坍塌平台段以及密实段。铝蜂窝在坍塌平台段应变不断增加，而应力基本保持不变，形成平台应力，是能量吸收的主要部分，也是研究的重点，此阶段的平均应力就称为铝蜂窝的平均塑性坍塌应力[10]。

图2 铝蜂窝典型应力-应变曲线

1.1 准静态压缩下铝蜂窝平均塑性坍塌应力推导

图3所示为铝蜂窝基本折叠单元示意图。铝蜂窝在压缩过程中会形成重复性的折叠单元，一个基本折叠单元长度为2H(称为折叠波长)，一般以基本折叠单元为研究对象分析铝蜂窝的异面压缩性能。

图3 铝蜂窝基本折叠单元示意图

荣吉利等[10]以如图4所示的六边形铝蜂窝单元为研究对象，此单元包括4个双倍壁厚的面和8个单倍壁厚的面。

图4 单个完整铝蜂窝单元

根据能量守恒定律及能量最低原理，得到了Tresca屈服准则下的准静态平均塑性坍塌应力

(2)

以及Mises屈服准则下的准静态平均塑性坍塌应力

(3)

该模型只体现了铝蜂窝结构平均塑性坍塌应力与铝蜂窝材料屈服应力、铝蜂窝结构的胞壁厚度t和胞元边长l间的关系，只适用于准静态压缩工况，没有考虑动态压缩工况中材料应变率效应对铝蜂窝结构坍塌变形的影响。

1.2 动态压缩下铝蜂窝平均塑性坍塌应力推导

根据Cowper-Symonds模型[12-14]，考虑铝蜂窝材料应变率效应对力学性能的影响，其动态平均塑性坍塌应力

(4)

为了计算铝蜂窝单元的应变率，将一个正六边形单元等效为半径为R的薄壁圆筒来处理[11]。铝蜂窝的六边形单元(不含支线)包含2个双倍壁厚的面和4个单倍壁厚的面，所以根据周长相等原则，有

2πR=4l+2×2l=8l

(5)

可以求得等效圆的半径

(6)

基本折叠单元如图5所示。

图5 基本折叠单元

基本折叠单元上任意一点M(距离塑性铰距离为m)的应变为

(7)

一个基本折叠单元折叠完成后，α=π/2，所以，折叠单元的平均应变

(8)

由此可求得应变率

(9)

式中：T为压缩时间，vm为平均压缩速度，H为折叠半波长。

对于落锤冲击加载，初速为v0，由于压缩时间很短，可近似认为vm=v0/2，由此可得应变率

(10)

(11)

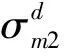
(12)

2 铝蜂窝异面压缩试验验证

2.1 铝蜂窝试验件相关参数

为了验证以上理论推导的正确性，本文以5052铝蜂窝为试验对象，做了若干准静态及动态压缩试验。5052铝蜂窝的材料参数如表1所示。

表1 5052铝蜂窝材料参数

5052铝蜂窝的物理参数如表2所示。

表2 5052铝蜂窝物理参数

正六边形铝蜂窝在加工成所需形状时，其横截面中每个六边形单元很难精确切割成完整的单元，针对图6中的铝蜂窝结构常采用图中虚线所示的分割方法将其分割成Y型单元来计算其横截面面积。

图6中Y型单元的面积SY

(13)

正六边形铝蜂窝在切割成正六边形形状时，其Y型单元的个数NY

NY=6n2+12n+6

(14)

式中：n=(N-1)/2，N为正六边形形状铝蜂窝最长边上完整的六边形单元个数(由于铝蜂窝切割成正六边形形状，故N为奇数，图6中N=3)。

图6 六边形铝蜂窝结构Y型单元划分

结合式(13)和式(14)可得正六边形铝蜂窝结构横截面积S,

(15)

本文采用的5052铝蜂窝试件，N=11，S= 4489.476 mm2。

2.2 铝蜂窝的准静态压缩试验

对铝蜂窝试件进行了3次准静态压缩，得到的力与位移曲线如图7所示，其中力是铝蜂窝受试验机压缩的力，位移是铝蜂窝顶端的位移也是铝蜂窝的压缩变形量。试验中压缩速度为2 mm/min。从图7可以看出,铝蜂窝在准静态压缩下力-位移曲线具有很好的一致性，塑性坍塌力约为3919 N。

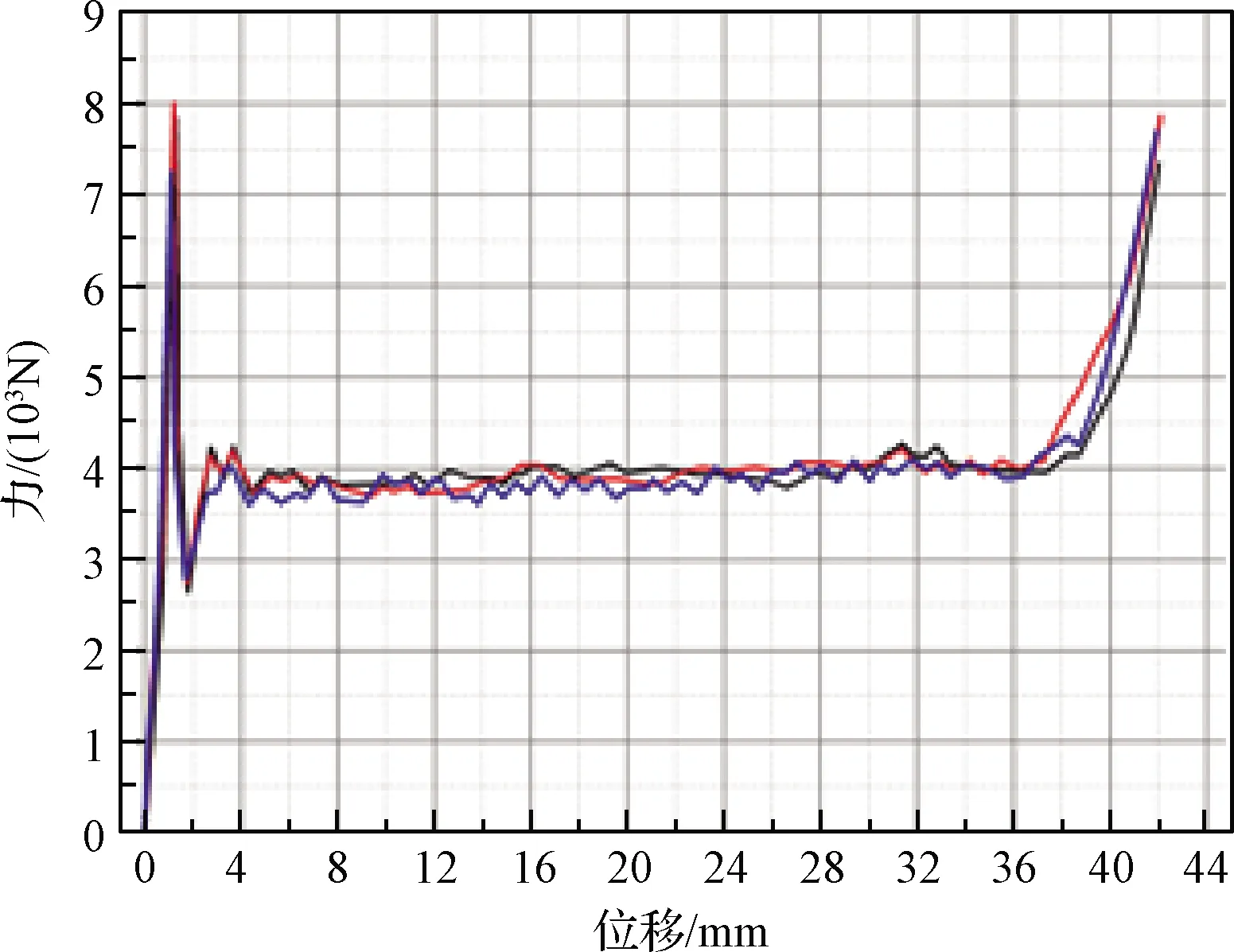
图7 5052铝蜂窝准静态压缩力-位移试验曲线

铝蜂窝的平均塑性坍塌应力的试验结果及理论值如表3所示，从表3可以看出：经典的半经验公式即式(1)相对于试验值偏小，误差为17.068%；式(3)的计算结果相对于试验值偏大，误差为-6.529%；式(2)的计算结果与试验结果高度吻合，误差仅为0.916%。

表3 5052铝蜂窝准静态压缩试验结果与理论计算对比

2.3 铝蜂窝动态异面压缩试验研究

2.3.1试验工装

采用WANCE落锤冲击试验机测量铝蜂窝动态压缩性能，试验工装如图8所示。

图8 铝蜂窝动态压缩试验工装

在中质锤体下落压缩铝蜂窝前一刻通过速度传感器测量中质锤体的压缩速度，试验的反作用力通过中质锤体中的力值传感器进行测量。为了防止损坏力值传感器，在中质锤体下面安装了缓冲器，中质锤体从一开始接触铝蜂窝到与缓冲器接触整个过程行程约为24 mm(即铝蜂窝的有效压缩长度)。

2.3.2动态压缩试验结果

对铝蜂窝试件进行了如表4所示的6种不同工况下的试验，试验中设定了锤体不同的压缩能量，并在试验中用测速传感器对锤体压缩铝蜂窝前一刻的压缩速度进行精确测量，不同工况下的压缩速度测量结果如表4所示。

表4 动态压缩试验工况

6种工况下5052铝蜂窝动态压缩力-位移曲线如图9所示。在工况1中，由于压缩能量较小，中质锤体没有与缓冲器接触，铝蜂窝并未到达密实阶段。在工况2～6中，由于压缩能量较大，中质锤体从刚接触铝蜂窝开始运动24 mm后即与缓冲器相接触，其后的测量值并不准确，即工况2～6中力-位移曲线在24 mm内有效。锤体与缓冲器接触后，部分力被缓冲器吸收，越往后压缩缓冲器吸收的能量越大，作用在铝蜂窝上的力越小，直到为零，故导致工况2～6中力-位移曲线在24 mm以后力值逐渐减小。

图9 铝蜂窝动态压缩力-位移试验曲线

3 铝蜂窝动态压缩的有限元仿真校验

3.1 有限元模型的建立

有限元仿真采用ANSYS/DYNA软件，使用全尺寸有限元模型对铝蜂窝试件进行有限元分析。如图10所示，铝蜂窝自由放置在刚性面上，上刚性面质量为中质锤体总质量8.8 kg，并施加不同工况下对应的初始速度。铝蜂窝采用Belytschko-Tsay型壳单元，材料模型采用与应变率相关的随动塑性材料模型，铝蜂窝之间采用单面接触，铝蜂窝的材料参数见表1及表2。

图10 铝蜂窝有限元模型

3.2 仿真计算结果

在工况1的压缩速度下，铝蜂窝在变形过程中的应力变化情况如图11所示。从图11(b)～(f)可以看出：铝蜂窝在压缩过程中顶部的应力值最大，底端其次，中间最小。铝蜂窝在很短的时间内(约0.05 ms)，上部应力达到最大值，此值对应铝蜂窝弹性变形阶段的峰值压力。在随后的压缩过程中铝蜂窝顶部、中部以及底部的应力值均减小并趋于平稳，图11(c)～(f)中上部的最大应力值对应铝蜂窝的塑性坍塌应力。铝蜂窝中部除了在其刚受到压缩的很短时间内应力较大外，其余时间均较小。图11中铝蜂窝的应力分布及变化情况与实际压缩过程中铝蜂窝的变形过程吻合。

图11 铝蜂窝变形过程

图12为铝蜂窝在工况1～工况6下的力-位移仿真曲线。值得说明的是在计算工况1和工况2时，由于初始速度较小，铝蜂窝压缩的时间较长，为了节约计算资源，并未计算铝蜂窝的整个压缩过程。

图12 铝蜂窝动态压缩力-位移仿真曲线

4 理论、试验及仿真结果讨论

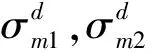
表5 各工况下试验应力、计算应力、仿真应力对比

图13 动态压缩下铝蜂窝应力-压缩速度曲线

5 结 论

本文所做工作可对动态压缩下铝蜂窝的异面压缩性能研究提供一定的工程借鉴，以便为铝蜂窝吸能装置的设计提供理论指导。