UltraFlex太阳电池阵的结构优化

吴志培，刘志超，宋逸博，荣吉利，辛鹏飞

(1.北京理工大学宇航学院，北京 100081；2.中国运载火箭技术研究院，北京100076；3.空间物理重点实验室，北京 100076；4.北京空间飞行器总体设计部，空间智能机器人系统技术与应用北京市重点实验室，北京 100094)

0 引 言

随着航天事业的发展，在航天器轻质化及大展收比的新需求下，薄膜结构因具有质量轻、面积大、高展收比等优点而越来越多地被应用到航天器上[1-3]。圆形太阳翼是一种典型的空间薄膜结构，在继承了薄膜结构优点的同时，由于柔性较强且展开面积较大，结构的展开过程稳定性及展开锁定后易受太空外在环境激励影响的性质，给圆形太阳翼的设计及应用提出了挑战。因此，针对圆形太阳翼进行结构优化，研究不同结构参数对展开过程稳定性及结构固有频率的影响，具有重要的实际工程价值和意义。

最早的圆形柔性太阳翼是20世纪90年代由美国ABLE公司(现为ATK公司)研发而出的UltraFlex太阳电池阵，是一种圆形柔性毯式太阳电池阵；该电池阵具有结构紧凑、质量轻、功率质量比高、转动惯量低、展开刚度高和扩展性好等特点[4]。此前，NASA已成功进行了UltraFlex柔性电池阵的地面展开试验及模态试验，并将其多次成功应用于航天器中[5-9]。由于电池阵地面试验模拟太空环境难度较大，耗时较长，实际设计过程中常使用数值分析的方法进行仿真计算，并指导设计工作。然而文献[5-9]并未展开圆形太阳翼结构参数对结构展开过程稳定性及模态的灵敏度研究分析，相关优化内容未见记载。

目前，国内对于圆形超柔太阳电池阵的研究和研制仍处于起步状态[10-11]。文献[12]针对UltraFlex超柔太阳电池阵，利用SAMCEF有限元软件对其展开过程进行动力学仿真分析，通过分析系统展开过程中能量变化曲线，研究了不同转角驱动函数对其展开过程稳定性的影响；文献[13]考虑结构的接触碰撞，基于绝对坐标方法建立了刚柔耦合的UltraFlex动力学模型，对系统的展开动力学进行了研究。虽然文献[12-13]开展了圆形太阳翼的展开驱动方式的研究，但尚未涉及不同结构参数对系统展开过程稳定性及模态的影响研究。

本文基于UltraFlex太阳电池阵，利用有限元软件SAMCEF Field建立全尺寸模型，采用膜单元模拟柔性翼面，在充分考虑展开过程中刚柔耦合因素以及薄膜自接触碰撞问题的情况下，通过分析电池阵展开过程中结构应力状态、结构能量变化曲线，以承重梁材料、斜梁开口高度、斜梁位置、梁截面高度及厚度5种结构参数为优化变量，研究不同结构参数的承重梁对太阳电池阵展开过程稳定性的影响；同时，通过模态仿真计算获得5种结构参数对结构模态的影响。最后给出了相应的结构优化指导意见。

1 动力学仿真

1.1 有限元模型

根据UltraFlex-175太阳电池阵几何尺寸使用SAMCEF Field进行建模。太阳电池阵结构主体由10片折叠梯形膜片和12根承重梁组成；承重梁由上方支撑梁和下方斜梁组成。支撑梁与膜片在共节点处绑定，折叠时支撑梁并排布置，其截面通常为矩形截面。薄厚度均为0.1 mm，支撑梁长度均为2750 mm，初始时相邻梁间距为6 mm。10片折叠的梯形膜片首尾相连，形成一个扇形的折叠结构，在中心电机的驱动下展开后呈正十边形，如图1所示。

UltraFlex太阳电池阵结构的主要承重构件和主要系统刚度组成成分是由支撑梁AB和斜梁CD组合而成的承重梁，如图2所示，支撑梁与斜梁在交汇点D处固支。

图2 承重梁示意图

研究结构参数对系统展开过程稳定性及模态的影响主要是探究不同结构参数承重梁的影响。在设计该承重梁时，许多参数同时对结构的稳定展开和模态产生影响，其中包括承重梁材料、斜梁位置(由AD表征，初始800 mm)、斜梁开口高度(由AC表征，初始200 mm)、梁截面高度和厚度(初始分别为20 mm和4 mm)。

1.2 支撑梁应力分析

UltraFlex太阳电池阵展开过程中，薄膜与支撑梁之间会发生拉扯行为。若展开速度过快导致运动幅度过大，会使得由胶结方式组成的碳纤维梁等承受剪切力发生结构破坏，进而导致展开失败。针对该现象，对太阳电池阵的展开过程中支撑梁的剪切应力进行分析；该算例从开始展开到完全展开共用时60 s，为了研究展开后的残余振动，在完全展开后保持锁定状态6 s。

图3给出了动能、外力做功、应变能随时间变化的曲线。由图可知，外部电机做功，将能量转化为动能和应变能。可以见到约在t=55 s之前，外力做功几乎全部转为动能，太阳翼的应变能近乎为0；之后急剧变大，原因是薄膜张紧产生了薄膜变形，此时支撑梁受到拉扯。图4是系统支撑梁最大及最小剪切应力随时间变化曲线，可发现在薄膜未发生变形之前，即约在t=55 s之前，支撑梁几乎不受剪切应力；而后从0.1 MPa急剧增大到0.82 GPa，并保持峰值不变，这与图3中的应变能变化趋势相吻合。由此可见，结构设计时，应考虑由胶结方式组成的碳纤维梁等的胶结方式及剪切强度极限，确保结构安全展开。

图3 太阳翼展开过程系统能量变化曲线

图4 支撑梁切应力变化曲线

2 展开过程稳定性分析与优化

本节对不同结构参数的模型逐一进行仿真，以结构展开动能变化作为参考变量进行数据分析，判定各相关变量对结构展开过程稳定性的影响，并获得变量可优化区间；最后综合各影响因素，进行交叉参数优化，获得使结构展开过程稳定性最好的变量参数。

2.1 支撑梁材料对展开过程稳定性影响

柔性太阳电池阵承重梁材料应用最广泛的是碳纤维和铝合金，两种材料的电池阵结构展开过程动能变化关系如图5所示。由图可知，铝合金支撑梁结构质量较大，因此整体动能大，加速阶段动能增长不平滑，减速阶段动能曲线相对平滑但变化相对急促，不利于结构的顺利展开，容易影响航天器的姿态；相比之下，碳纤维支撑梁，获得动能较小，减速阶段动能曲线比较平滑，展开锁定后，残余振动的幅值较小，因此碳纤维梁的太阳翼结构展开过程稳定性更好。

图5 承重梁材料不同时太阳电池阵动能变化曲线

2.2 斜梁位置对展开过程稳定性影响

图6为斜梁在不同位置工况下电池阵的动能变化曲线。由图6可知，综合考虑斜梁位置不同对系统展开过程稳定性的影响及展开锁定状态下对残余振动的抑制效果发现，斜梁位置为1000 mm时，结构展开过程中总动能较小，展开前、后期动能变化幅度较小，结构展开平稳，并且展开锁定状态下，对残余振动的抑制效果较好。而斜梁位置为1200 mm时，仿真结果与1000 mm较为相近。考虑该工况的斜梁长度较大使得质量增加影响了系统的动能，因此可对斜梁位置为1000～1200 mm范围内进行进一步优化分析。

图6 斜梁位置不同时太阳电池动能变化曲线

2.3 斜梁开口高度对展开过程稳定性影响

图7为斜梁开口高度不同时电池阵的动能变化曲线，由图可知，斜梁开口高度对太阳翼展开过程中动能的变化影响较小，曲线变化趋势及展开效果基本一致，都能使太阳电池阵平稳展开。

图7 斜梁开口高度不同时太阳电池阵动能变化曲线

2.4 承重梁截面参数对展开过程稳定性影响

现有的太阳电池阵，承重梁截面通常选为矩形截面，方便收拢并减小体积。因此，承重梁的截面参数考虑截面厚度与截面高度，图8与图9分别为不同截面厚度与不同截面高度时太阳电池阵动能变化的曲线。支撑梁厚度越大，太阳电池阵结构的质量越大，动能随之增大，这与图8所示曲线趋势基本吻合；且各个厚度参数下的动能变化趋势比较吻合，可发现承重梁截面厚度对展开过程稳定性影响较小。

图8 承重梁截面厚度不同时动能变化曲线

图9 承重梁截面高度不同时动能变化曲线

从图9中可发现，承重梁的截面高度越大，太阳电池阵的质量越大，因而动能越大。综合而言，高度在20 mm时，系统运动过程中的总动能较小，残余动能相较可接受。同时可发现，当高度变大，其后期的动能震荡幅度较小。考虑到25 mm的工况导致质量增加影响系统动能，因此可以将梁截面高度控制在20～25 mm之间进行进一步仿真分析，获得最优的太阳翼展开过程中动能及展开锁定状态下残余振动幅度。

2.5 参数交叉优化分析

通过以上分析可知，承重梁材料为碳纤维时，结构刚度较大，展开过程的稳定性较好，对残余振动的抑制效果较好。承重梁截面厚度与斜梁开口高度对电池阵展开过程稳定性影响较小；斜梁位置与承重梁截面高度对电池阵的展开过程稳定性影响较大，因此对这两组参数进行交叉优化分析。系统所获得的最大动能和残余振动的幅值是分析太阳翼展开过程稳定性及残余振动抑制效果的两个重要指标，表1为交叉优化参数表

表1 UltraFlex太阳电池阵承重梁交叉参数优化表

从太阳电池阵展开过程中获得的最大动能、展开锁定时刻的动能以及残余振动动能的幅值综合考虑可知，1号、3号、7号、11号、13号和16号相对于其他工况，展开锁定后的动能较小，残余动能的幅值较小，因此对这六种工况下太阳电池阵的展开过程稳定性进行进一步分析。

图10为六种工况下太阳电池阵展开过程中动能变化的曲线。这六种工况由于承重梁质量不同，因此展开过程中动能的大小不同，但动能的变化趋势相似。t=45 s之前，太阳翼展开过程平稳；t=45～60 s之间太阳翼动能上下起伏，变化较为剧烈，这是由于太阳翼展开处于减速状态，薄膜结构由于惯性处于不断的波动，但7号工况动能变化的幅值最小；t=60～66 s之间，太阳翼完全展开后锁定，太阳翼的残余振动到66 s时基本都缩减到零，其中1号和7号的残余振动降到了最低。进一步考虑7号工况相较1号工况本身质量较大，易于产生较大动能，这六种工况中7号工况即斜梁位置为1100 mm、梁截面高度为20 mm时动能总量较小，展开后期动能变化最平稳，并且对残余振动的抑制效果最优，展开过程最稳定。

图10 六种工况下太阳电池阵动能变化曲线

3 模态分析与优化

通常太阳翼的低阶模态固有频率较低，因为容易受到环境干扰，产生剧烈振动，轻则影响航天器姿态，重则造成结构破坏。承重梁是太阳翼结构中刚度较大的部件，探究承重梁的结构参数对模态的影响规律可科学合理地优化太阳翼的低阶模态固有频率，对于圆形薄膜太阳翼的设计具有重要的指导意义。参考承重梁对运动稳定性的影响，本节中以碳纤维为材料，研究承重梁的结构参数对模态的影响。

3.1 斜梁位置对模态的影响

斜梁位置不同时，太阳翼的前四阶固有频率如表2所示。可见，随斜梁位置的增大，太阳翼的固有频率逐渐提高，但对第一阶频率影响较小。考虑太阳翼的一阶振型为面内振动，可见斜梁位置主要影响太阳翼面外刚度，对面内刚度的影响较小。此外，当斜梁位置为900 mm或1100 mm时，相对于800 mm，固有频率增幅较大，由位置增加导致的质量稍微变大可以接受，因此该模型实际应用时可适当增加斜梁位置。

表2 斜梁位置不同时太阳翼的前四阶固有频率

3.2 斜梁开口高度对模态的影响

表3给出了斜梁的开口高度不同时，太阳翼的前四阶固有频率。观察数据发现，随开口高度的增加，太阳翼的固有频率具有增大的趋势，但总体来看变化不大，呈较稳定的状态；说明斜梁开口高度对模态的影响较小，可忽略不计。

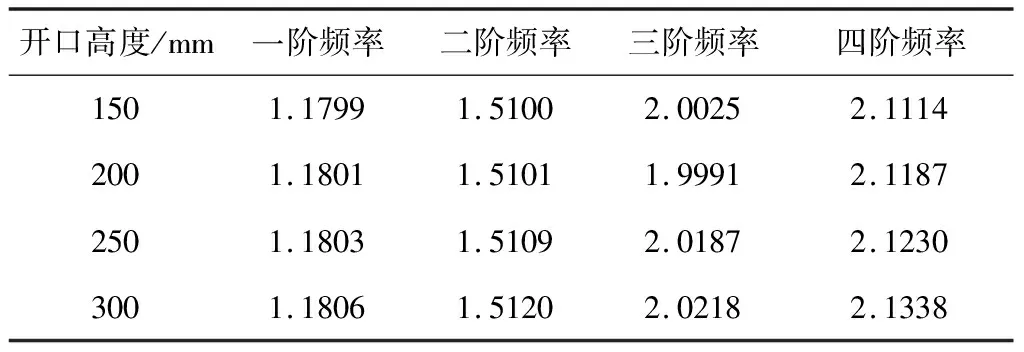
表3 斜梁开口高度不同时太阳翼的前四阶固有频率

3.3 承重梁截面参数对模态的影响

承重梁厚度不同时，太阳翼的前四阶模态如表4所示。可知，随梁厚度的改变，太阳翼的后三阶固有频率改变不大，总体上呈稳定趋势。而太阳翼的第一阶固有频率受梁厚度的影响较大，由于太阳翼的第一阶模态为面内振动，可见梁的厚度影响了太阳翼面内刚度。因此，要提高结构第一阶固有频率可适当增加承重梁截面厚度。

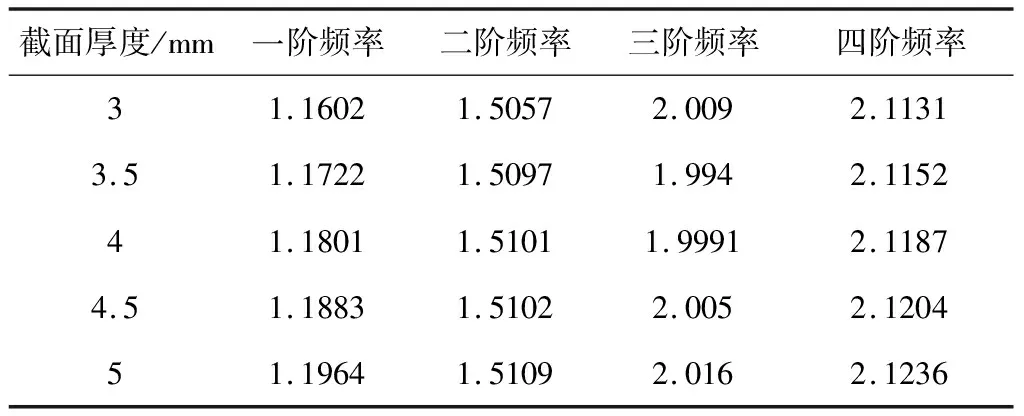
表4 承重梁厚度不同时太阳翼的前四阶固有频率

承重梁截面高度不同时，太阳翼的前四阶固有频率如表5所示。可以发现，太阳翼的固有频率总体随着梁截面高度的增加而增大，变化趋势较为平缓。当截面高度为15 mm时，太阳翼的第一阶频率大于截面高度为20 mm时，这是由于面内刚度增加对系统的影响小于质量增加带来的影响。参考后三阶频率的增加趋势，说明梁截面高度主要影响太阳翼的离面刚度，但影响不大。

表5 承重梁截面高度不同时太阳翼前四阶固有频率

4 结 论

本文采用有限元软件SAMCEF Filed对UltraFlex超柔太阳电池阵进行结构优化。以构件材料和开口高度、斜梁位置、承重梁截面高度及厚度5种参数为优化变量，对UltraFlex超柔太阳电池阵进行了多种工况的展开动力学仿真和模态计算，经过研究获得主要结论如下：

1)太阳电池阵在结构展开过程后期，太阳毯与支撑梁之间的拉扯会导致支撑梁的剪切应力在5 s内从0.1 MPa急剧增大到0.82 GPa，并保持峰值不变；因此，在进行结构设计时，应考虑材料的剪切强度极限，防止结构破坏；

2)5种结构参数中，承重梁材料、斜梁位置与承重梁截面高度对太阳电池阵的展开过程稳定性影响较大，斜梁开口高度和梁截面厚度影响相比之下可忽略不计；根据参数交叉优化结果，当承重梁材料为碳纤维，斜梁位置为1100 mm，梁截面高度为20 mm时，展开过程稳定性最好；

3)斜梁位置和承重梁截面高度主要影响系统的面外刚度，因此对系统一阶频率影响很小，对第二、三、四阶影响较大；承重梁截面厚度主要影响系统的面内刚度，因此主要影响系统一阶频率；而斜梁开口高度对系统模态影响可忽略不计。其中，斜梁位置为900 mm或1100 mm时，相对于800 mm，固有频率增幅较大；而承重梁截面厚度由3 mm到3.5 mm，一阶频率涨幅最大，之后以约7‰线性增长。考虑到几种参数的增加对系统质量增加的影响，综合考虑，在结构设计时可适当增加斜梁位置和承重梁截面厚度，同时避开承重梁截面高度增加导致第一阶固有频率减小的副作用。