Zygmund型空间上的加权微分复合算子

秦 春

（怀化学院初等教育部，湖南怀化 418008）

1 引言

设D为复平面C上的单位圆盘，H（D）表示D上的全纯函数全体，S（D）表示D上的全纯自映射全体.对任意的正实数α，定义

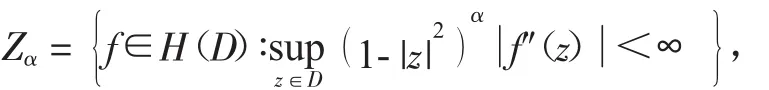
称为Zygmund-型空间.易知Zygmund-型空间在范数

下为Banach空间.当α=1时，Z1=Z称为经典的Zygmund空间.

令 φ∈S（D），u∈H（D），定义 H（D）上的加权微分复合算子为：

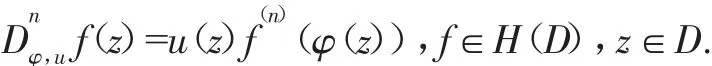
Cowen.C，Maccluer.B在文[1]中研究了解析函数空间上复合算子Cφ的相关内容.叶善力在文[2]中研究了经典的Zygmund空间上的微分复合算子DCφ的有界性.刘超、侯晓阳在文[3]中研究了经典的Besov空间到经典的Zygmund空间上的加权复合算子Cφ，u的有界性和紧性.陆恒与张太忠在文[4]中研究了α-Zygmund空间到β-Bloch空间上的加权复合算子Cφ，u的有界性和紧性.陈伟与许毅在文[5]中研究了经典的Besov空间到Zygmund-型空间上的加权微分复合算子的有界性和紧性.刘永民和于燕燕在文[6]中研究了经典的Hardy空间到Zygmund-型空间上的加权微分复合算子的有界性和紧性.更多不同空间上加权微分复合算子的相关结果见文[7-13].

2 主要结果

定理 1 令 0＜α，β＜∞，n∈N*，u∈H（D），φ∈S（D），则为有界算子的充分必要条件是

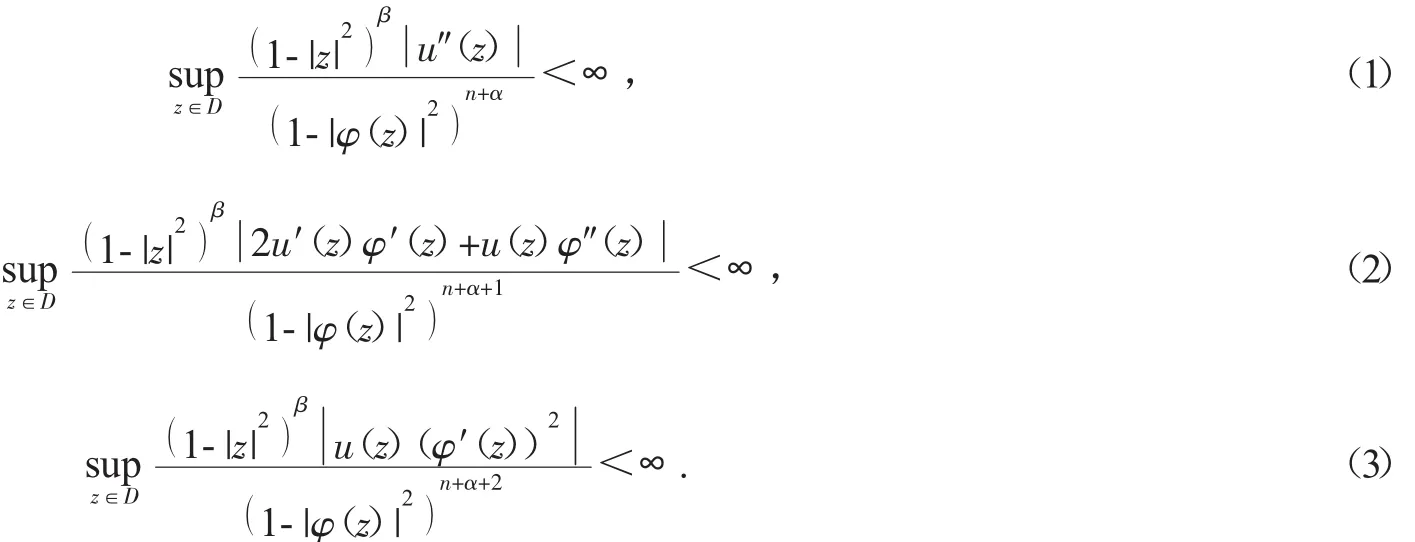
定理 2 令 0＜α，β＜∞，n∈N*，u∈H（D），φ∈S（D），则∶Zα→Zβ为紧算子的充分必要条件是为有界算子，并且

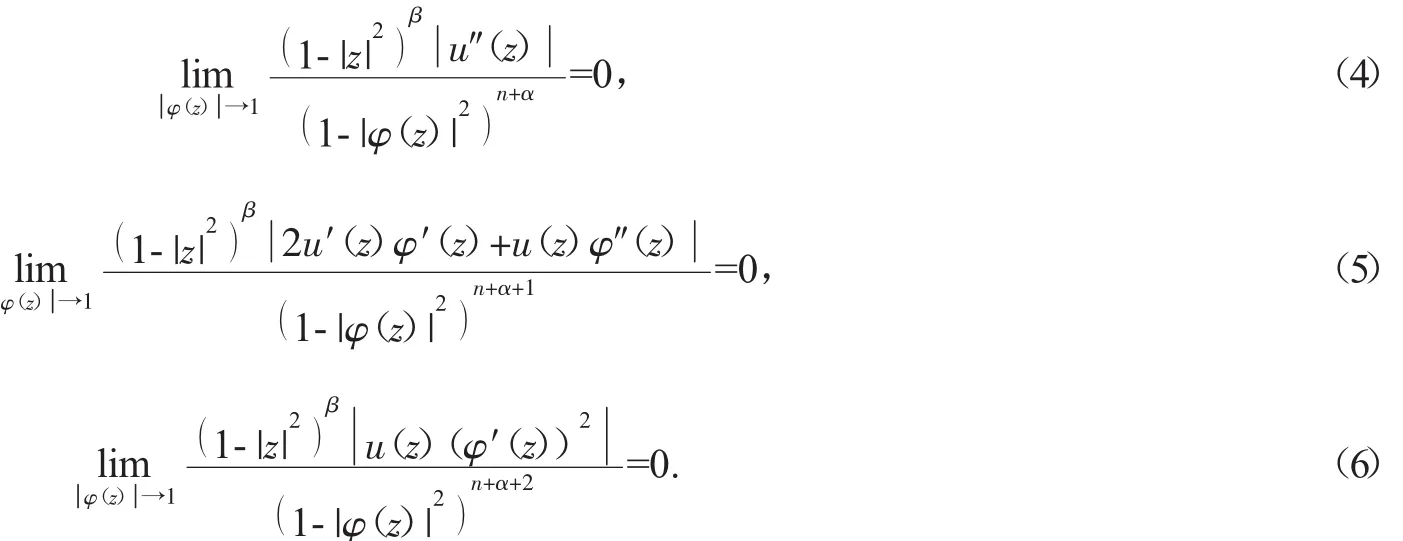
3 定理的证明

在证明之前，给出所需引理和相关推论.

引理 1[14]如果 f∈Bα，α＞0，那么

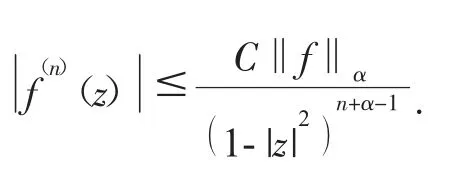
引理 2 如果 f∈Zα，那么 f′∈Bα.

推论 1 如果 f∈Zα，α＞0，那么

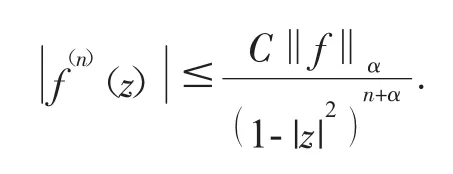
引理 3[15]设 α＞1，β＞1，u，φ∈H（D），且如果

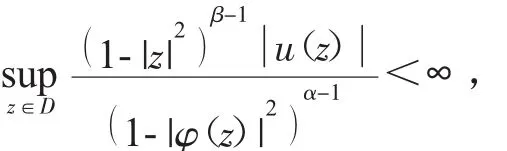
那么

定理2的论证：首先证明充分性.对Zα中任意有界序列｛fk｝，有fk在D的紧子集上一致收敛于0.由引理4可知，只23需证明‖Dnφ，ufk‖β→0，k→∞.下面不妨设‖fk‖α＜1.

由（4）式、（5）式及（6）式可知，∀ε＞0，∃δ∈（0，1），s.t.，当 0＜|φ（z）|＜1 时，有：

从而｛fk（z ｝）在D的紧子集上一致收敛于0.结合引理2与（17）式，得到：

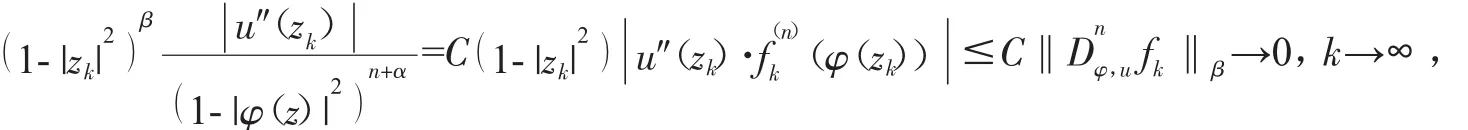
故

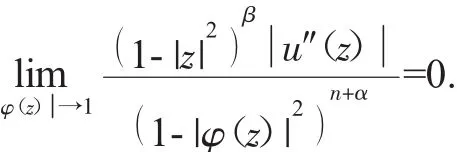
从而（4）式得证.对（5）式和（6）式，分别取（12）式和（13）式定义检测函数，采用同样的方法，可知结论成立.