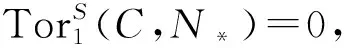相对余挠自由模和对偶Auslander转置的若干注记

何东林

(陇南师范高等专科学校 数信学院，甘肃 陇南 742500)

Auslander-Reiten理论在Artin代数和同调代数中扮演着重要的角色，Auslander转置是该理论的重要工具之一.利用Auslander转置，Auslander和Bridger[1]引入了n-挠自由模，并得到特定条件下有限生成模的一个逼近理论.Tang X和Huang Z[2]给出了Auslander转置的对偶概念，称之为对偶Auslander转置.半对偶模是相对同调代数中的重要模类之一，许多学者先后对其进行了研究，并得到了很好的结论[3-8].特别地，Holm和White[4]将半对偶模的概念推广到任意一对结合环R和S上，并利用这一工具研究了关于半对偶双模的Auslander类ΑC(S)和Bass类BC(R).Tang X和Huang Z[2]借助对偶Auslander转置，介绍了关于半对偶双模RCS的n-C-余挠自由模，并得到Bass类BC(R)的一个等价刻画.自然而然地，可考虑关于n-C-余挠自由模和对偶Auslander转置的更多问题，比如性质、刻画等等.基于以上研究背景，本文主要给出n-C-余挠自由模和对偶Auslander转置的若干性质和刻画，并研究短正合列0→L→M→N→0中各项的n-C-余挠自由性之间的关系.

1 定义与引理

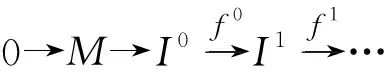
注1：① 对任意整数m≥n≥1，有m-C-余挠自由模一定是n-C-余挠自由模；②n-C-余挠自由模关于有限直和及直和因子封闭.

引理1[2]以下结论成立：

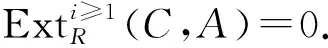
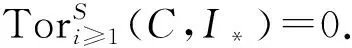
引理2[9]设图1为左R-模行正合交换图，

则 1) 有正合列Kerα→Kerβ→Kerγ→Cokerα→Cokerβ→Cokerγ.

2) 图1中当A→B为单同态时，1)中Kerα→Kerβ也为单同态；当B′→C′为满同态时，1)中Cokerβ→Cokerγ也为满同态.

引理3[2]设M是左R-模，则以下结论成立：

1)M是1-C-余挠自由的当且仅当M是C-余无挠的.

2)M是2-C-余挠自由的当且仅当M是C-余自反的.

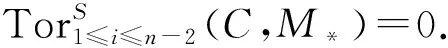
引理4[2]设M是左R-模，则存在正合列:

2 主要结论

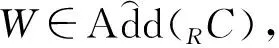
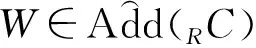
0→An*→…→A1*→A0*→W*→0，

考虑行正合交换图，如图2:

定理2 设M是左R-模且n≥1，则以下条件等价：

1)M是n-C-余挠自由模； 2) 存在HomR(C,-)下正合的正合列:

An-1→…→A1→A0→M→0，其中Ai∈Add(RC)(0≤i≤n-1)；

证明1)⟺2) 由文献[2]中命题3.6易证.

HomR(C,N)⊕HomR(C,N′)≅HomR(C,N⊕N′)=HomR(C,C(I))≅S(I)，

所以HomR(C,N)是投射左S-模.从而有Add(RC)⊆PC成立.

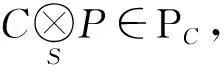
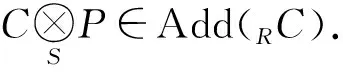
综上所述，PC=Add(RC).

命题1 设I是内射左R-模，则对任意整数n≥1，都有I是n-C-余挠自由模.

证明由引理1中结论2)及引理3易证.

命题2 设F是FP-内射左R-模，则对任意整数n≥1，都有F是n-C-余挠自由模.

证明由F是FP-内射左R-模及文献[10]中定理2.1中(2)知，F∈BC(R).根据文献[2]中定理3.8可得，对任意整数n≥1有F是n-C-余挠自由模.

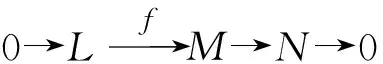
1) 如果L和M是n-C-余挠自由模，那么N是n-C-余挠自由模.

2) 如果L和N是n-C-余挠自由模，那么M是n-C-余挠自由模.

3) 如果M是n-C-余挠自由模且N是(n+1)-C-余挠自由模，那么L是n-C-余挠自由模.

由引理2可得正合列:

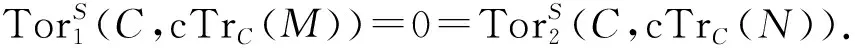
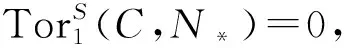
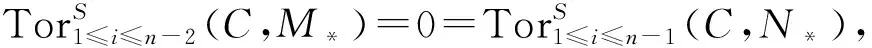
由引理3及定理3易得如下推论.

1) 如果L和M是C-余无挠模，那么N是C-余无挠模；2) 如果L和N是C-余无挠模，那么M是C-余无挠模；3) 如果M是是C-余无挠模且N是是C-余自反模，那么L是C-余无挠模.