混沌时变时滞系统的有限时间脉冲同步
陈亚英,姚凤麒
(安徽工业大学 电气与信息工程学院,安徽 马鞍山 243032)
目前关于系统同步的研究大多数都集中在渐近同步方面[1-5],即要求耦合系统的状态在无限时间内相同.与渐近同步不同,有限时间同步是指当系统的初始状态在某一范围内时,系统的状态在一定的时间内不超过某一预先给定的界限[6-11].在实际的工程应用中,人们除了关注耦合系统在无限时间内的渐近同步外,更感兴趣的是在给定时间内系统是否能够满足一定的暂态性能.近年来,有限时间同步吸引了大量的学者研究[6-13].例如,Ali M等[6]讨论了带Markovian复杂动态网络的有限时间同步问题;Mei J等[10]针对参数不匹配的复杂动态网络研究了有限时间同步问题;Wu K N等[12]针对脉冲随机反应扩散系统的有限时间同步问题展开研究;Bao H等[13]研究了两个不同时滞混沌系统的有限时间同步问题.
然而,对于混沌系统而言,即使两个混沌系统是相同的,只要初始条件有细微的差异,这两个系统就不会达到同步.在实际生活中,初始条件恰恰是不能完全确定的,这就使得混沌同步的研究变得极为重要.自从Pecora等[14-15]于20世纪90年代提出了驱动响应同步方法实现了两个混沌系统的同步,自此以后混沌同步成为工程应用领域的研究热点[13,16-20].随着对混沌系统控制的深入研究,脉冲控制同步法作为一种用来控制混沌的新方法,已经被很多学者证实是非常有效的.它相对于连续控制方法性能更好、成本更低且易于实施[1-2,6].在实际系统中,从脉冲对系统同步性能的影响来说,可以分为去同步脉冲和同步脉冲.在现有的研究文献中,大部分假设它们是分开发生的[4,12].由于在实际系统中,不同的时刻受到不同的脉冲扰动,可能导致它们同时存在.因此,同时考虑去同步脉冲和同步脉冲构成的混合脉冲具有重要研究意义[1,21-22].例如,Wong W K等[1]研究了具有混合脉冲复杂网络的同步问题.在复杂网络中同时考虑去同步脉冲和同步脉冲,建立了统一处理去同步脉冲和同步脉冲的框架.
基于以上讨论,受Wong W K等[1]研究的启发,拟针对参数一致的驱动响应混沌系统有限时间脉冲同步问题展开研究.与Wong W K等人的研究不同,本文设计了一种混合脉冲控制器包含线性反馈部分和脉冲控制部分,其中反馈控制增益可以抵消不利脉冲带来的影响;并且本文考虑的是混沌系统有限时间脉冲同步问题.首先,在系统模型中同时考虑了去同步脉冲和同步脉冲,设计了一种合适的混合脉冲控制器;其次,通过选择合适的Lyapunov函数,利用有限时稳定性理论、比较引理和平均脉冲区间法,给出了系统有限时间同步的充分条件;最后,给出一个数值算例表明了理论结果的有效性.
1 系统描述及准备
考虑如下具有时变时滞的驱动系统:
(1)
其中:x(t)∈n表示系统的状态变量;A,B,D∈n×n为已知常数矩阵;C=(cij)n×n1=(c1,c2,c3,…,cn1);cj(j=1,2,…,n1)是C的第j列;τ(t)为时变时滞,且满足0≤τ(t)≤τ;非线性函数n.
以式(1)为驱动系统,则相应的响应系统形式如下:
(2)
这里,y(t)∈n是系统的状态变量;u(t)是控制输入.
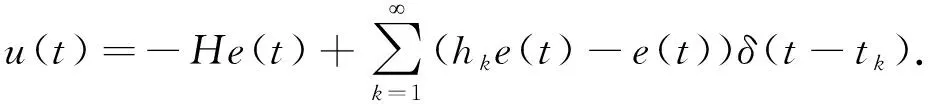
(3)
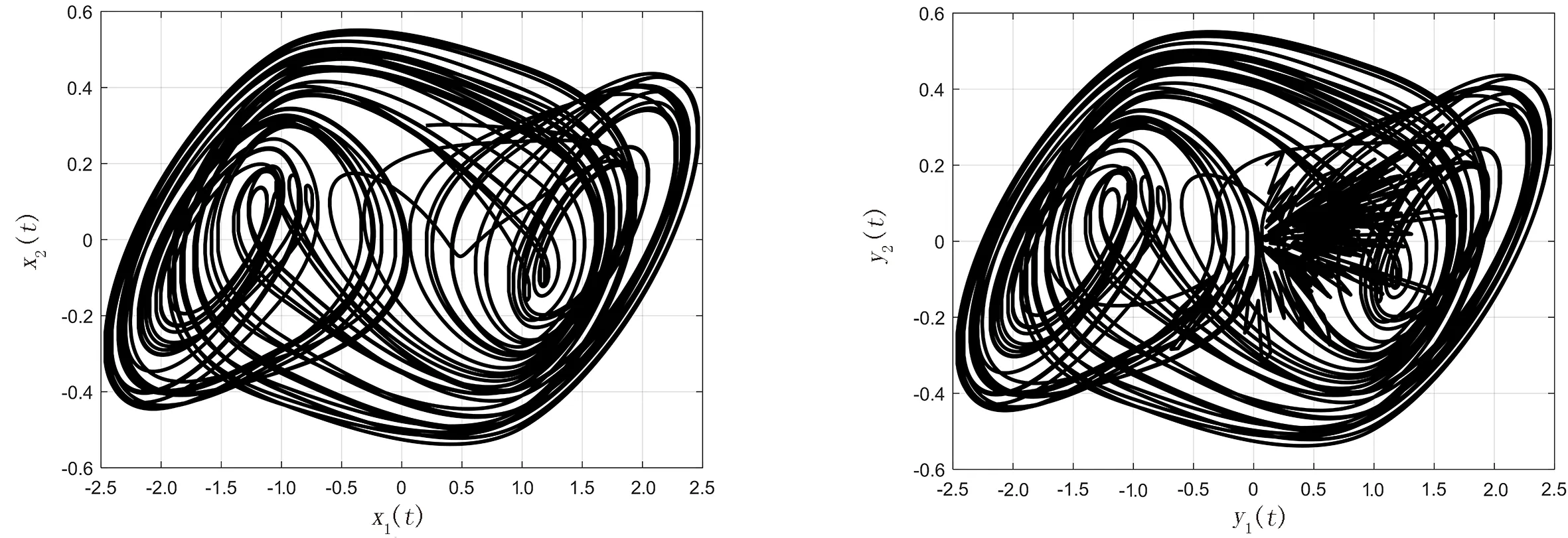
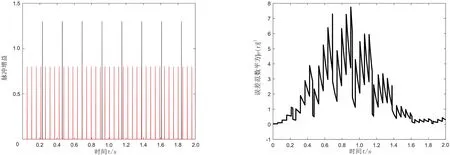
这里,脉冲序列{tk}(k∈)满足0 (4) 这里,g(CTe(t),x(t))=f(CTy(t))-f(CTx(t)),假设e(t)在t=tk处是左连续的.为了简化,认为e(t)在t0=0处是连续的. 注1 文献[23]通过设计混合脉冲控制器研究了神经网络指数同步问题,然而所考虑的脉冲增益在不同的时刻是不变的.本文所设计的控制器脉冲增益在不同的时刻是不同的.其中包括反馈控制部分和脉冲控制部分,可以通过调整反馈控制增益H的大小来使同步条件成立.因此,本文设计的混合脉冲控制器(3)更具有适用性. 注2 当脉冲强度hk>1时,脉冲效应是抑制同步的,即去同步脉冲;当脉冲强度hk<1时,脉冲效应是促进同步的,即同步脉冲.特别地,当hk=1时是非活动脉冲,非活动脉冲对系统的同步既无危害又无益处.因此本文主要研究去同步脉冲和同步脉冲对系统同步的影响. 误差系统(4)的初始条件定义为:e(s)=φ(s),-τ≤s≤0. (5) 这里,φ(·)∈C([-τ,0],n). 在介绍主要结果之前,先介绍如下主要假设、引理和定义. 假设1 假设fi(·)属于一个扇区[0,l],即fi(ξ)(fi(ξ)-lξ)≤0.则: 因此可以接着推出: (6) 假设2 假设去同步脉冲和同步脉冲的脉冲强度分别从有限集{μ1,μ2,…,μN}和{v1,v2,…,vM}中取值,满足μi>1,0 (7) 则脉冲强度为μi的去同步脉冲的平均脉冲区间不小于εi,脉冲强度为vj的同步脉冲的平均脉冲区间不大于ρj. 注3 在文献[4,12,24]中,研究者对去同步脉冲和同步脉冲是分开考虑的.本文同时考虑去同步脉冲和同步脉冲构成的混合脉冲.因此,本文所构建的系统模型更具有普遍性. 在本节中将推出驱动系统(1)和响应系统(2)有限时间脉冲同步的充分条件.利用Lyapunov函数法可建立如下定理. (8) |eaταR-a|T+eaταRτ≤lnm2-lnRm1. (9) 证明选择李雅普诺夫函数:V(t)=eT(t)e(t). 首先,当t∈(tk-1,tk](k=1,2,…)时,沿着误差系统(4)对V(t)求导: (10) 由引理2和式(6)可知,存在正数α,β使得: (11) (12) 将式(11)、(12)代入式(10),可得: (13) (14) 对于任意ε>0,令v(t)是如下脉冲时滞系统的唯一解: (15) 从引理1可知V(t)≤v(t),对∀t≥0.根据参数变易法,v(t)可以表示为: (16) (17) (18) 由定义1和式(18)可得: (19) 从式(16)和式(19),可以推出: (20) 令U(t)=eatv(t),则: (21) 令ε→0,由引理3可以推出: (22) 再由条件(9),立即可得:V(t)≤v(t)≤Rm1elnc2-lnRc1=m2,t∈[0,T]. (23) 即: ‖e(t)‖2≤m2,t∈[0,T]. (24) 即驱动系统(1)和响应系统(2)是关于(m1,m2,T)有限时间同步的. 证毕. 注4 当脉冲效应抑制同步时,为了保证同步,则要求脉冲之间的时间间隔不能太小.在以往的研究结果中,大多采用tk-tk-1≥ε,通过调整ε的值来保证去同步脉冲发生的不频繁.本文同时考虑去同步脉冲和同步脉冲,即使去同步脉冲频繁发生,可以增大ρj使同步脉冲频繁发生来抵消去同步脉冲的影响,驱动响应系统仍能同步. 注5 对于大多数的脉冲信号,脉冲发生的时间间隔不是相等的即它不是均匀分布的.倘若脉冲区间的上界比较大,下界比较小,在文献[3,12,16]中,作者采用脉冲间隔的上下界来表示脉冲发生的频率可能导致所得的结果具有一定的保守性. 当混合脉冲控制器考虑的是时不变脉冲时,即在不同的时刻脉冲强度是不变的.此时μi≡μ1,εi≡ε1,vj≡v1,ρj≡ρ1,其中i=1,2,…N,j=1,2,…M,满足μ1>1,0 (25) |eaταR-a|T+eaταRτ≤lnm2-lnRm1. (26) 对于本文研究的混沌系统有限时间脉冲同步问题,将用一个数值算例来验证理论结果的有效性. 考虑将如下蔡氏电路作为驱动系统[16]: (27) (28) (29) 将采用脉冲控制器(3)来实现驱动系统(28)和响应系统(29)的有限时间同步,定义e(t)=y(t)-x(t)为驱动响应系统的同步误差,得到如下误差系统: (30) 图1 驱动系统(28)图2 响应系统(29)Fig.1 Drive system(28) Fig.2 Response system(29) 图3 脉冲序列图4 误差系统轨迹(30) Fig.3 Impulse sequence Fig.4 The trajectory of error system(30) 图5 脉冲间隔为ρ1=0.2时的脉冲序列图6 脉冲间隔为ρ1=0.2时的误差系统轨迹(30) 通过设计混合脉冲控制器研究了混沌系统的有限时间脉冲同步问题.在系统模型中,同时考虑去同步脉冲和同步脉冲构成的混合脉冲,因此更具有普遍性.并且本文所设计混合脉冲控制器包括线性反馈部分和脉冲控制部分,可以通过调节反馈控制增益来使系统达到有限时间同步.最后通过一个数值算例验证了理论结果的有效性.本文考虑的是参数一致的混沌系统的有限时间脉冲同步问题.然而,在实际系统中很难做到参数完全一致.因此,在今后的研究中,将深入研究参数不匹配对混沌系统的影响.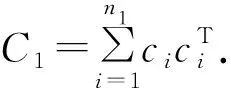
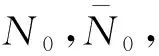
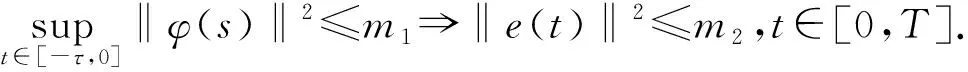
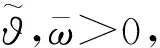
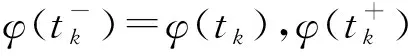
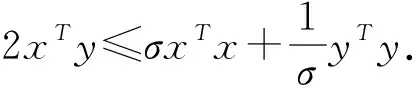
2 主要结果
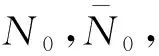
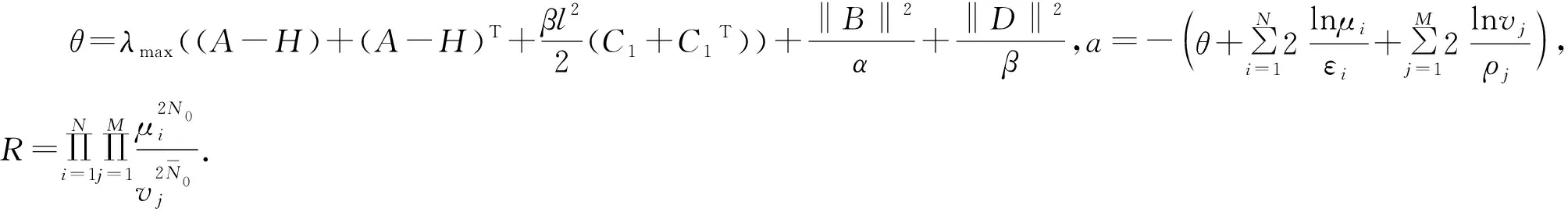
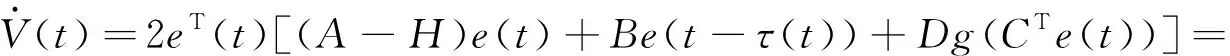
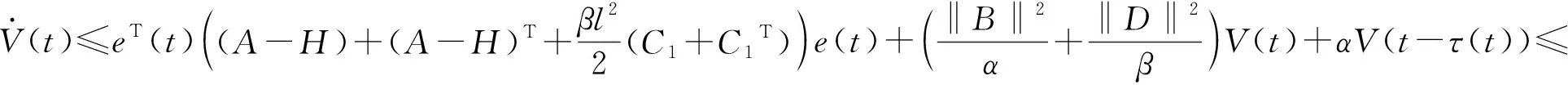
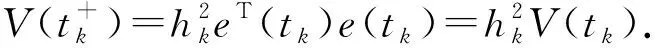


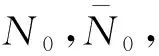
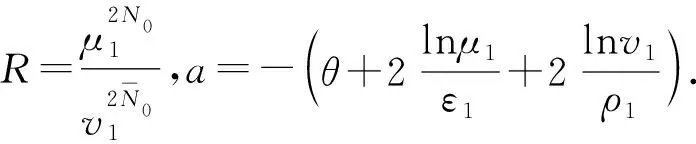
3 数值算例

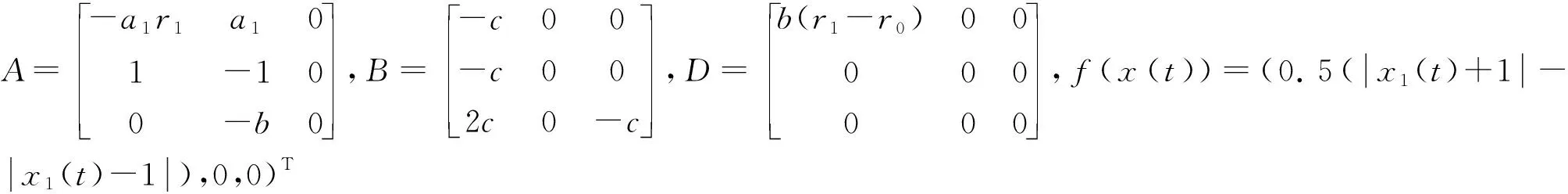
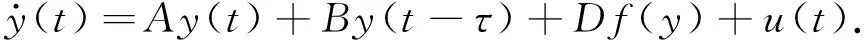
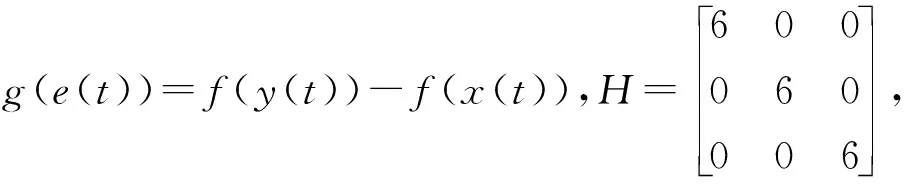

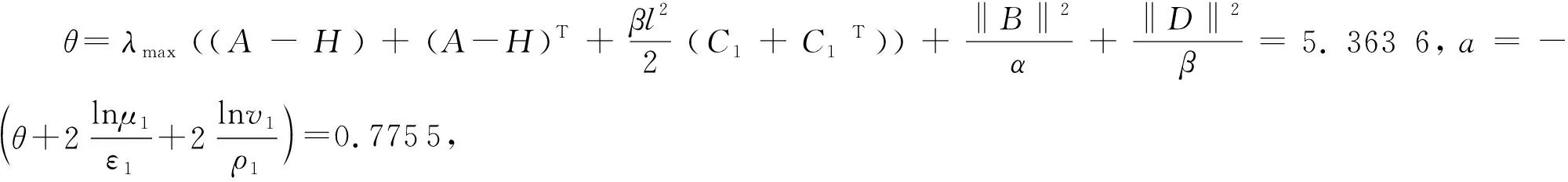
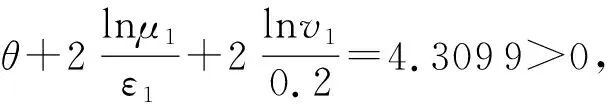
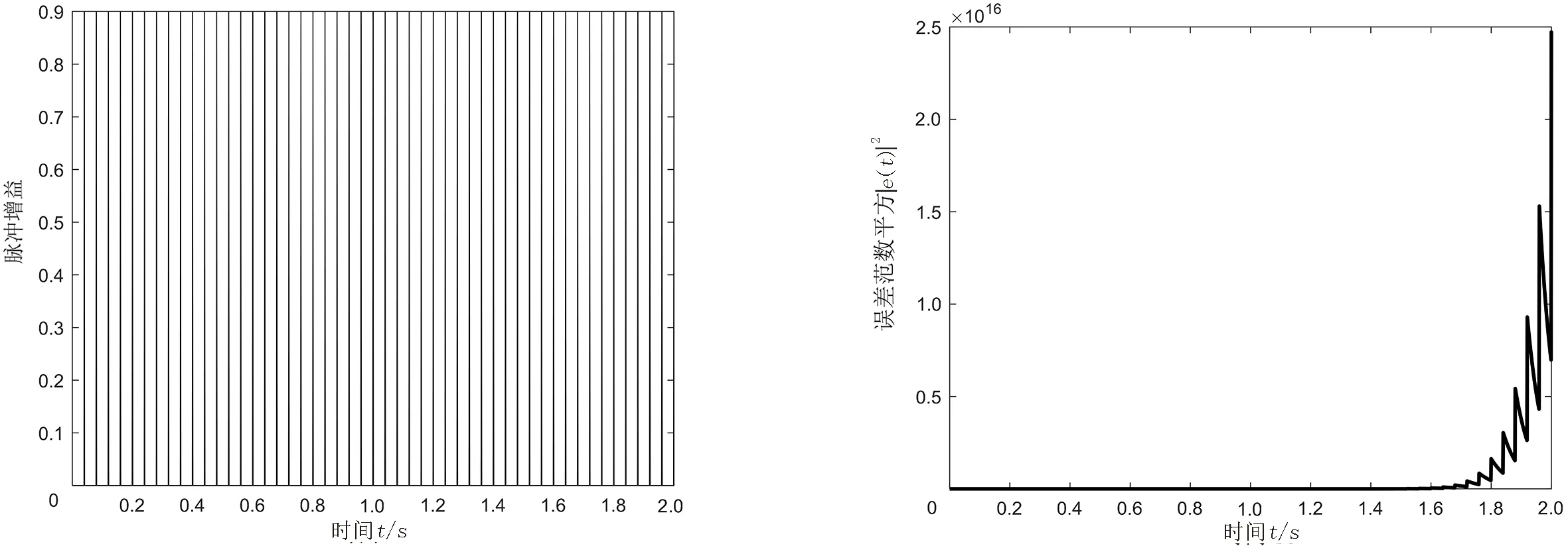
4 结论

