基于等效介质原理的宽角超材料吸波体设计*

吴雨明 王任 丁霄 王秉中

(电子科技大学， 应用物理研究所， 成都 611731)

超材料吸波体的吸波性能会受到电磁波入射角度的影响， 角度不敏感的吸波材料设计一直是吸波材料设计的难点之一. 本文基于等效介质原理设计了一种宽入射角超材料吸波体. 超材料吸波体单元由竖直放置在理想导体(PEC)上的双面开口谐振环组成， 谐振环开口处加载集总电阻R 和集总电容C， 其中电阻R 用于调控超材料的等效电磁参数， 电容C 用于调控超材料的谐振频率和实现单元小型化. 当TE 波(横电波， 电场方向与入射面垂直的平面电磁波)照射时， 电阻R = 4000 Ω， C = 1.5 pF， 在1.59 GHz 处， 本文设计的宽角超材料吸波体实现了70°内90%以上的吸波率， 当入射角度达到75°， 也仍然有85%以上的吸波率， 并且基于等效介质原理的理论分析结果和仿真结果及测量结果都基本符合； 当TM 波(横磁波， 磁场方向与入射面垂直的平面电磁波)照射时， 电阻R = 1200 Ω， C = 1.5 pF， 此时需将超材料单元旋转90°， 在1.59 GHz 处， 本文设计的宽角超材料吸波体实现了70°内90%以上的吸波率， 当入射角度达到75°， 也仍然有85%以上的吸波率.测试结果基本与仿真结果符合. 此外， 当电容C 发生改变而其余参数不改变时， 本文设计的超材料吸波体在新的谐振频率处仍然具有同样的宽角吸波性能， 具有宽频带的工作特性.

1 引 言

吸波材料指能够在一定程度上吸收自由空间中电磁波的自然材料或者由电磁结构构建的超材料吸波体. 传统的吸波材料是由自然界存在的铁氧体、碳粉等吸收剂混合一些热塑料、环氧树脂等非金属基体而成的一类涂覆于目标表面的吸波材料.其往往有着吸收频带窄、吸收角度小、质量重、剖面高等缺点. 自2008 年Landy 等[1]提出超材料吸波体的概念后， 超材料因其自身的强大可塑性， 历经10 多年的发展， 许多研究者在带宽、剖面、极化敏感度等方面取得了很多的研究成果[2-13]. 与传统吸波材料相比， 超材料吸波体在很多性能方面有着明显的优势. 目前大多数电磁超材料吸波结构主要关注点仍然在带宽方面， 对吸波材料吸收来波的角度研究较少. 实际上， 自由空间中电磁波的入射角度和极化是难以预知的， 因此需要吸波材料具有很宽的吸收角度和极化不敏感度才能有效地吸收电磁波. 部分学者通过构建角度不敏感的结构来实现宽角吸波[14-25]. 尽管已找到一些合适的单元结构来实现宽角度吸波， 但是一直没有统一的设计理论和设计方法. 文献[26-28]通过理论推导带有金属地板的单层介质的电场和磁场， 并结合边界条件，建立了TM 波照射下反射系数和等效电磁参数的关系， 其中文献[26]采用双面螺旋环的结构验证了理论的可行性. 文献[29]在文献[26]的基础上补充了TE 波照射时的理论推导并分析了实现宽角吸波效果所需的等效电磁参数[29]， 但并没有给出实际案例. 在传统的人工介质研究中， 一般通过调整单元尺寸和相关材料参数来控制超材料的等效电磁参数. 但该种方式不够灵活， 能够调节的自由度低， 在要求超材料小型化、低剖面等特殊场景下其能够调节的自由度又会大大下降， 难以精确调控到所需的等效电磁参数. 因此， 需引入更多的易于调节的自由度来精确控制等效电磁参数以满足设计的要求. 在本文研究内容中， 通过引入集总电阻调控等效电磁参数并利用S 参数反演技术提取等效电磁参数[30]， 此外还引入电容， 一方面为了调控超材料的谐振频率， 另一方面为了实现单元小型化， 最终完成宽角度吸波材料的设计.

文献[29]的宽角理论分析指出， 影响TE 波和TM 波照射时吸波材料的宽角吸波效果的关键因素分别由µr1x，h和µr1y，h决定， 其中µr1x指的是TE 波照射下提取的x方向等效磁导率，µr1y指的是TM 波照射下提取的y方向等效磁导率，h指的是等效介质的厚度. 基于此， 本文设计了一种宽角度超材料吸波体. 超材料单元由竖直放置在PEC上的两面均有开口谐振环结构的介质组成， 在环开口处加载集总电阻和集总电容控制超材料的等效磁导率和谐振频率. 该结构单元周期P为4.5 mm ×4.5 mm， 高度h为2.8 mm. 在谐振环开口处加载4000 Ω 电阻和1.5 pF 的电容， 提取TE 波照射下未加载金属反射板的等效磁导率， 在1.59 GHz 处，µr1x=3.19−j15.3， 此时厚度为0.0148λ， 单元周期为0.024λ× 0.024λ. 根据文献[29]的理论公式，计算在该条件下的吸波效率与入射角度的关系曲线， 理论分析结果与仿真结果及实测结果基本符合. 在谐振环开口处加载1200 Ω 电阻和1.5 pF 的电容， 提取TM 波照射下未加载金属反射板的等效磁导率， 在1.59 GHz 处，µr1y=1.07−j5.14 ， 在该条件下， 同样计算在该条件下的吸波效率与入射角度的关系曲线， 理论分析结果与仿真结果及实测结果基本符合. 仿真和测试结果显示： TE 波照射时， 在1.58 GHz 附近实现70°内90%以上的吸波率； TM 波照射时， 在1.6 GHz 处实现70°内90%以上的吸波率. 由于加工的误差， 实测结果相比仿真结果有细微的频率偏移， 但基本满足设计要求.此外， 本文设计的超材料吸波结构虽然需更换电阻R才能在TE 波和TM 波分别照射时使吸波材料都达到宽角吸波的目的， 但是并不需要重新调整单元结构的尺寸及介质等相关参数. 传统的吸波材料随着入射角度的增大， 其谐振频率会发生严重的频率偏移现象， 但本文中设计的超材料吸波体谐振频率随着入射角度的变化非常微小， 几乎可以忽略不计， 具有较好的频率稳定性. 此外， 当加载的电容C发生变化而其他参数不变化时， 超材料吸波体在新的谐振频率处仍然具有同样的宽角吸波效果， 具有宽频带工作的特性.

2 宽角超材料吸波体设计

2.1 超材料吸波体仿真结果及理论结果分析

本文设计的宽角超材料吸波体模型如图1(a)所示， 由竖直放置在PEC 地板上的双面开口谐振环组成， 两面谐振环具有180°的旋转对称性， 开口处都加载有集总电阻R和集总电容C， 目的是为了有效调节超材料的谐振频率以及等效磁导率.介质板材采用KB-6150 FR4 型号的板材， 介电常数4.4， 损耗角正切0.02， 厚度t= 0.8 mm， 高度h= 2.8 mm， 谐振环开口间距s= 0.8 mm， 环的宽度d= 0.4 mm， 环的长度L= 4 mm， 环的外宽度W= 2.2 mm， 单元的周期P= 4.5 mm.

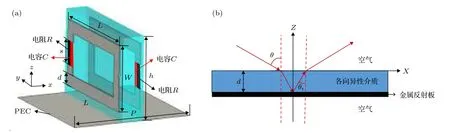
图1 单元模型和理论模型 (a)宽角超材料吸波体单元模型； (b)理论分析模型Fig. 1. Unit cell and theoretical model： (a) Wide-angle metamaterial absorber unit cell； (b) theoretical model.

超材料吸波体的吸波率用A(ω) 表 示，A(ω) 由以下公式计算得到：

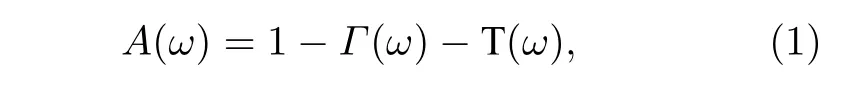
其中，Γ(ω) 表 示吸波材料的反射系数， T (ω) 表示吸波材料的透射系数. 当吸波材料的反射系数和透射系数都很小时， 超材料吸波体就能够获得很高的吸波率. 在本文的超材料吸波体模型中， 超材料下方放置有PEC 地板， 使其透射系数为0， 此时影响其吸波率的因素只有反射系数一项， 只需尽可能地降低其反射系数就能获得高的吸波率. 在文献[29]中， 推导出了TE 波和TM 波分别照射时单层带反射地板的吸波材料的反射系数表达式， 理论模型如图1(b)所示， 反射系数由(2) 式计算.

根据(2)式，θ表示电磁波入射角度， TE 波和TM波照射时吸波材料的宽角吸波效果分别由µr1x，h和µr1y，h决定. 实际上当吸波材料的厚度确定时，µr1x和µr1y成为制约宽角度吸波效果的最关键因素. 传统超材料往往通过调整单元结构的尺寸和形状来调控其等效电磁参数， 但此种方法对等效电磁参数的调控自由度较低， 对等效电磁参数的调控精确度也较低.

本文通过引入集总电阻来增加等效磁导率的调节自由度， 另外还引入集总电容来调节超材料的谐振频率， 电阻和电容都加载在谐振环的开口处，如图1(a)所示. 图2(a)给出了TE 波照射时超材料吸波体的谐振频率随电容C的变化， 此时开口处加载的电阻R为4000 Ω， 当TM 波照射时， 将超材料单元绕Z轴旋转90°， 此时开口处加载的电阻R为1200 Ω， 图2(b)给出了TM 波照射时超材料吸波体的谐振频率随电容C的变化. 从两幅图可以看出， 随着电容值的升高， 超材料吸波体的谐振频率随之下降. 加载的电容可以有效地调节超材料的谐振频率， 并不需要通过调整单元的结构尺寸， 实现了小型化的目的.

从(2)式可以看出， 实现宽角吸波效果的关键是能够精确调控超材料的等效磁导率， 使其反射系数在宽角度的范围内都能保持很小的数值. 因此，文中引入了集总电阻来增加等效磁导率的调控自由度. 本文采用CST 软件进行全波仿真， 利用S 参数反演计算等效磁导率. 根据理论模型， 本文反演计算的等效磁导率是等效介质的本构参数， 并不包含地板， 因此在提取超材料的等效磁导率时，首先把PEC 去除， 仿真得到的S 参数再进行参数反演. 图3(a)和图3(b)给出了TE 波垂直照射时，等效磁导率实部和虚部随电阻R的变化， 图3(c)和图3(d)给出了TM 波垂直照射时， 等效磁导率实部和虚部随电阻R的变化. 从图3(c)和图3(d)可以看出， 当超材料的其他尺寸参数不发生变化时， 电阻R能够较为精确地控制实部和虚部的数值， 有利于后续宽角度吸波体的设计. 为了反映实际超材料吸波体的吸波效果随R的变化， 在超材料单元下方加载PEC， 仿真得到的吸波体反射系数如图3(e)和图3(f)所示

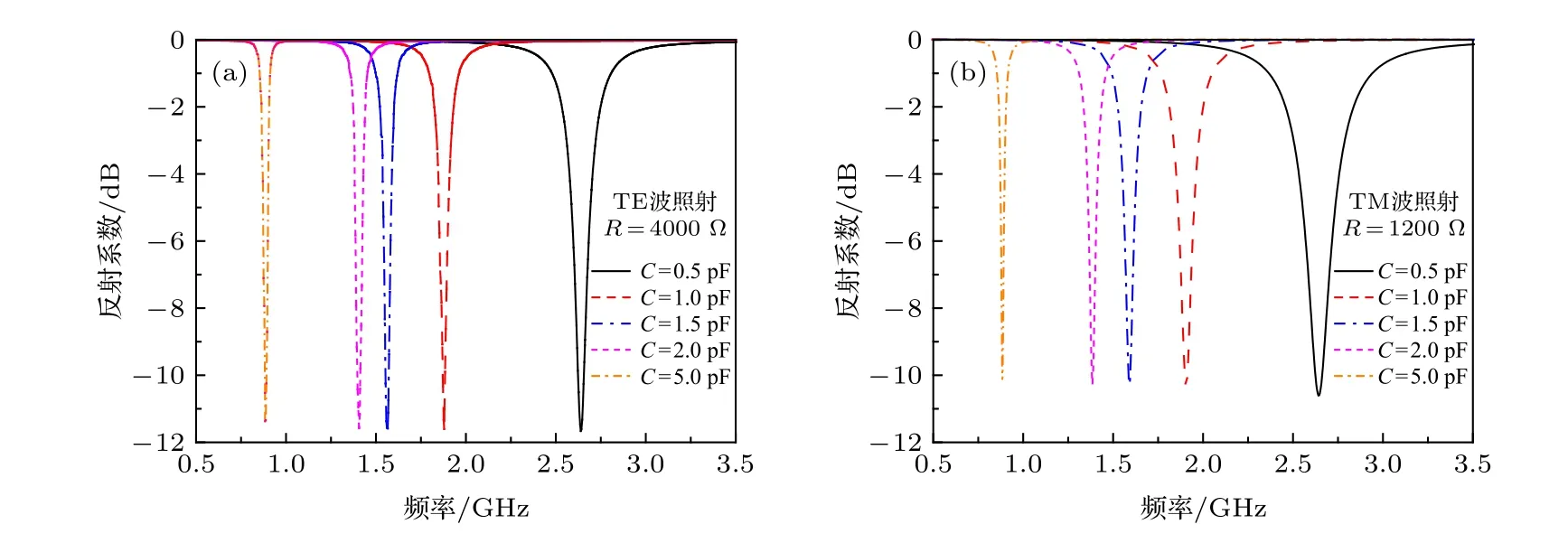
图2 超材料吸波体的谐振频率随电容的变化 (a) TE 波照射； (b) TM 波照射Fig. 2. Resonant frequency of metamaterial absorber varies with capacitance： (a) TE wave； (b) TM wave.

图3 超材料的等效磁导率虚部和实部以及超材料吸波体反射系数随电阻R 的变化 (a) TE 波照射时磁导率实部； (b) TE 波照射时磁导率虚部； (c) TM 波照射时磁导率实部； (d) TM 波照射时虚部； (e) TE 波照射超材料吸波体反射系数随电阻R 的变化；(f) TM 波照射超材料吸波体反射系数随电阻R 的变化Fig. 3. The imaginary parts and real parts of the equivalent permeability of the metamaterial and the reflection coefficient of the absorber varies with the resistor： (a) Real parts of the equivalent permeability under TE wave； (b) imaginary parts of the equivalent permeability under TE wave； (c) real parts of the equivalent permeability under TM wave； (d) imaginary parts of the equivalent permeability under TM wave； (e) the reflection coefficient of the absorber varies with the resistor under TE wave； (f) the reflection coefficient of the absorber varies with the resistor under TM wave.

图2 和图3 可以说明在谐振环开口处加载电阻和电容可以分别调控超材料的等效磁导率和谐振频率. 图2 和图3(e)及图3(f)给出的均为垂直入射下得到的反射系数， 并没有考虑斜入射时的反射系数， 但提取的等效磁导率代入(2)式中可以计算出反射系数与入射角度的关系. 为了获得宽角度的吸波效果， 需要选择能够使反射系数在宽角度时仍然较低的电阻阻值. 当TE 波入射时， 选择电阻R为4000 Ω， 电容C为1.5 pF， 提取的等效磁导率如图4(a)所示， 在谐振频点1.59 GHz 处，µr1x=3.19−j15.3，h约为0.0148λ. 当TM 波入射时， 选择电阻R为1200 Ω， 电容C为1.5 pF， 此时需将单元绕Z轴旋转90°， 提取的等效磁导率如图4(b)所示， 在谐振频点1.59 GHz 处，µr1y=1.07−j5.14 . 将提取的等效磁导率µr1x和µr1y分别代入(2)式中， 理论上计算出超材料反射系数随角度的变化. 图5 展示了上述条件下， TE 波和TM 波分别照射时加载PEC 地板的两种状态下的超材料吸波体的反射系数， 仿真结果显示： 入射角度在70°范围内， 在1.59 GHz 附近， 两种状态下的超材料吸波体在TE 波和TM 波分别照射时， 其吸收率都在90%以上； 当入射角度达到75°时， 超材料吸波体的吸波率都在85%以上. 将1.59 GHz 处的理论吸波结果与设计的超材料吸波体仿真结果对比， 结果如图6 所示. 当TE 波入射时， 在50°入射角以内， 理论结果比仿真结果低2dB 左右， 随着入射角度增大， 仿真的反射系数开始低于理论反射系数，当超过50°时， 仿真结果比理论结果低2dB 左右，虽然理论结果和仿真结果并没有完全符合， 但大体上理论结果和仿真结果是符合的； 当TM 波入射时， 在60°入射角范围内， 仿真的反射系数比理论结果低2dB 左右， 当超过60°入射角， 则理论的反射系数比仿真的反射系数低1dB 左右， 仿真结果和理论结果也基本符合.

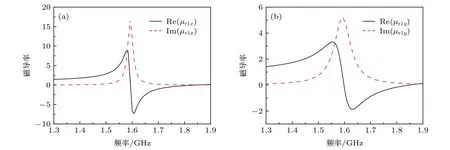
图4 等效磁导率 (a) TE 波照射； (b) TM 波照射Fig. 4. The equivalent permeability (a) TE wave； (b) TM wave.

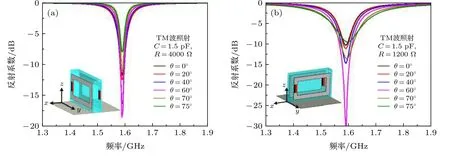
图5 超材料吸波体反射系数随角度的变化 (a) TE 波照射； (b) TM 波照射Fig. 5. The reflection coefficient of the absorber varies with incidence angle (a) TE wave； (b) TM wave.

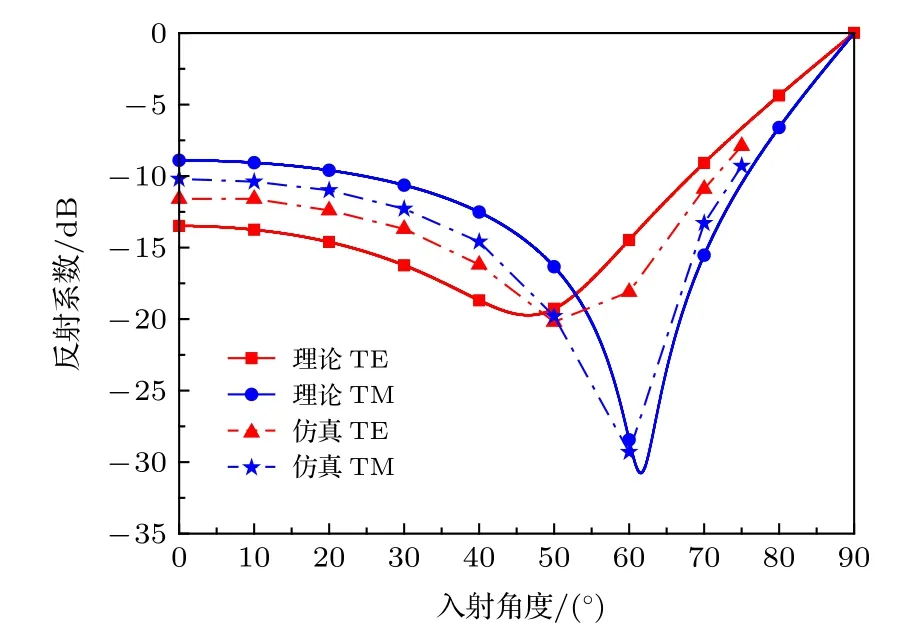
图6 理论计算结果与TE 波照射下R = 4000 Ω， C =1.5 pF 和TM 波照射下R = 1200 Ω， C = 1.5 pF 的仿真结果对比Fig. 6. Comparison of theoretical results and simulation results when R = 4000 Ω， C = 1.5 pF under TE wave and R =1200 Ω， C = 1.5 pF under TM wave.

2.2 实验系统及测量结果

超材料吸波体的测量方式通常都采用弓形法，测试系统如图7 所示. 测试环境在微波暗室中进行， 实物如图8(a)所示， 集总电阻元件型号是0201 型号的贴片电阻， 集总电容采用的是0603 型号NPO 材质的贴片电容， 板材金属表面工艺采用的镀锡， 电阻和电容贴片均采用的是SMT 贴片工艺， 样品尺寸是352 mm × 342 mm， 共74 × 72 个单元. 实测场景如图8(b)所示. 测试结果如图9 所示， 当TE 波照射时， 测试样品加载的电阻是4000 Ω，电容是1.5 pF， 该超材料吸波体在1.58 GHz 附近实现了70°内90%以上的吸收率； 而当TM 波照射时， 测试样品加载的电阻是1200 Ω， 电容同样是1.5 pF， 该超材料吸波体在1.6 GHz 附近实现了70°内90%以上的吸收率. 由于加工的误差， 实测中心频率相比仿真结果有略微的频偏， 但基本实现了本文的设计要求. 该超材料吸波结构具有宽角度的吸收特性.

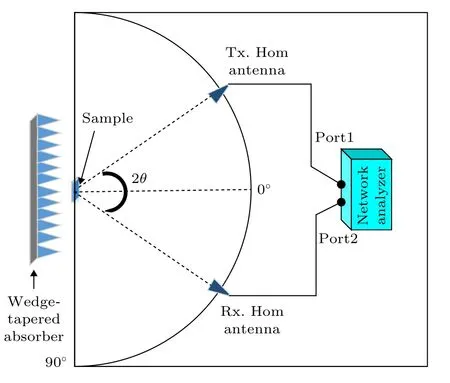
图7 测量系统Fig. 7. Measurement system.

图8 实物和实测场景 (a)样品； (b)测试场景Fig. 8. Sample and Measurement scene： (a) Sample； (b)measurement scene.

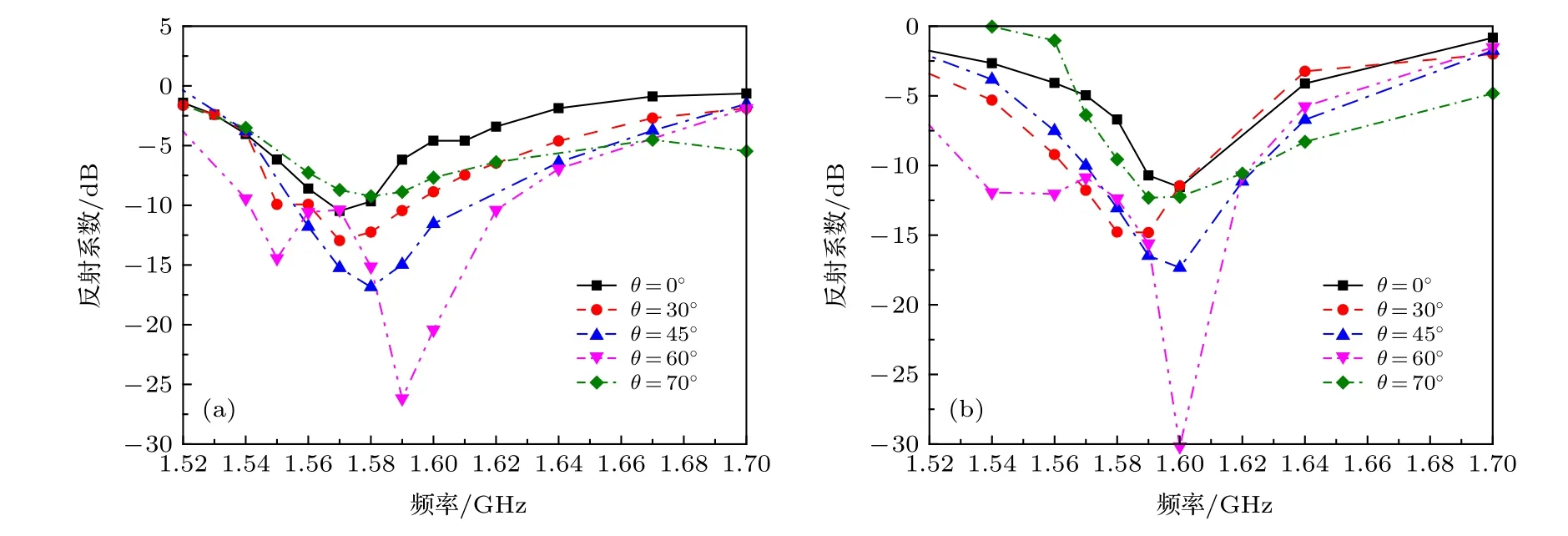
图9 测量结果 (a) TE 波照射； (b) TM 波照射Fig. 9. Measurement results： (a) TE wave； (b) TM wave.

3 讨论部分

角度不敏感超材料吸波体的设计往往面临两个难点： 一是随着入射角度的增加， 中心频率会往高频处偏移， 这是因为在一般情况下， 斜入射下的超材料单元的有效工作尺寸发生了改变； 二是随着入射角度的增加， 吸波效果会迅速恶化， 这是随着角度变化所引起的阻抗失配. 本文的超材料吸波体通过加载电容来控制其谐振频率， 当超材料不加载电容时， 本文中的结构会谐振在较高频段. 谐振频率的主要影响因素从结构转移到集总电容， 可以减小因为斜入射尺寸的变化所带来的频率偏移. 本文中电阻R的阻值并没有选择垂直入射时反射系数最小对应的电阻而是选择了中间值. 从阻抗匹配角度来看， 本文设计的宽角超材料吸波体其实是降低了小角度入射时的阻抗匹配度， 而使其在大角度入射时具有较高的阻抗匹配度. 因此， 能够在宽角度范围内实现高效吸波， 但是低角度吸波率会牺牲一部分. 表1 给出了本文工作与前人工作的性能对比， 本文设计的超材料吸波体在单元尺寸、剖面高度和吸收角度上都展现了较好的性能.

本文中， 电容C用以调节超材料吸波体的谐振频率. 从图2 可以看出， 当仅有电容C发生变化时， 其垂直入射时的反射系数值近乎保持不变. 在斜入射时如果也能保持同样的特性， 那么该结构具有宽频带的工作特性. 图10 展示了C= 0.5 pF和C= 5 pF 时宽角吸波数据， 从图中可以看出，不论C取何值， 超材料吸波体在新的谐振频率处仍然具有与加载1.5 pF 电容时同样的宽角吸波效果. 本文设计的超材料吸波结构在仅改变电容C的情况下能够在宽频带范围内实现宽角吸波效果.

表1 文献工作性能比较Table 1. Performance comparison among this work and other literatures.

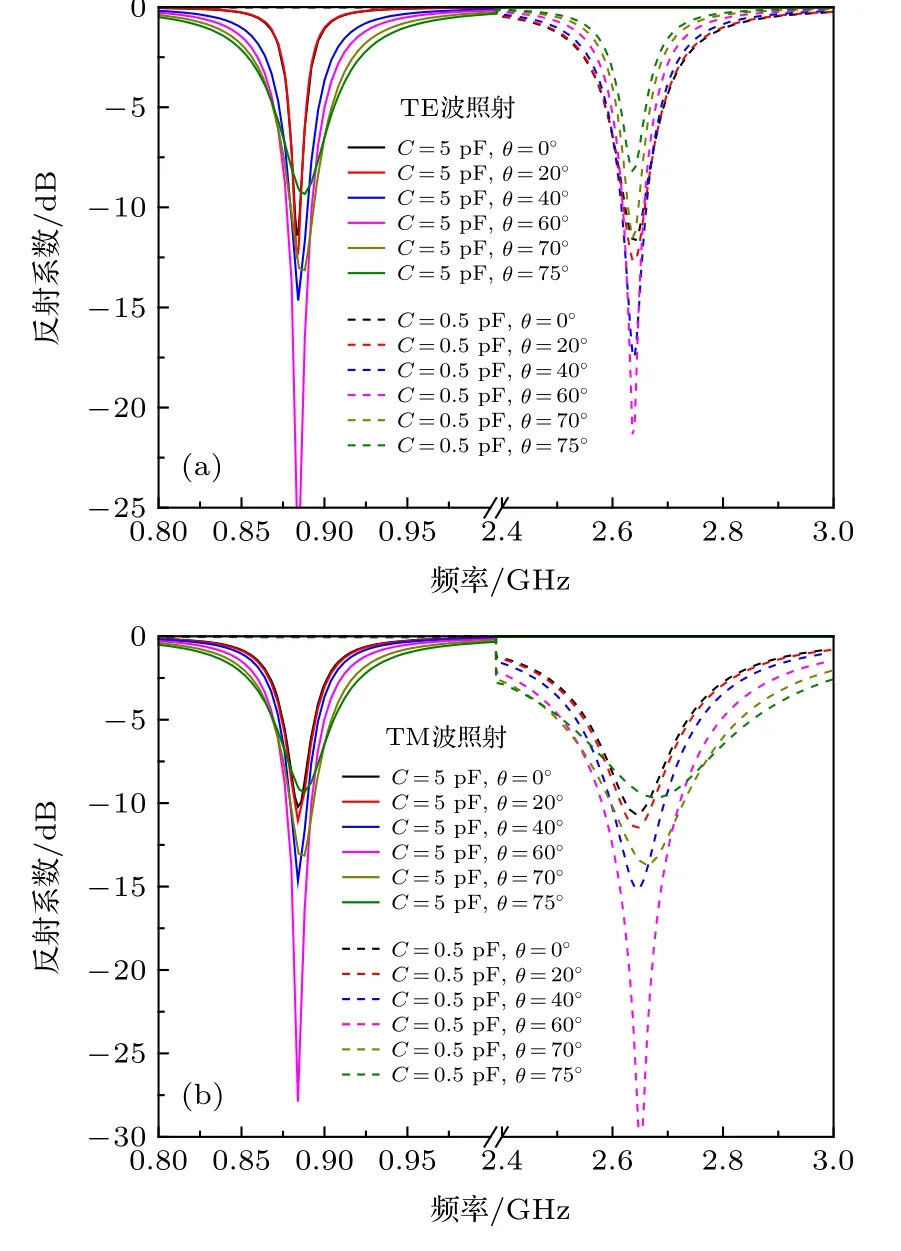
图10 不同容值下的宽角吸波效果 (a) TE 波照射； (b)TM 波照射Fig. 10. Performance of wide-angle absorber with different capacitance： (a) TE wave； (b) TM wave.

在实际应用中如能实现电容的连续调控， 超材料吸波结构便能够在宽频带范围内工作， 更具有实际应用价值. 本文设计的超材料结构在制备过程中是无法进行连续调节的， 单元结构是单开口谐振环， 开口上下电压始终是等压的， 无法为可变电容或可变电阻提供进行连续调节的偏置电压. 如果要对电容进行连续调控， 则需为其提供可用的偏置电压. 本文做了如下探索， 在开口环的另一端相应进行了开口设置， 并加载与左边同样的定值电阻和可变电容， 并设计了相应的直流偏置馈线， 如图11所示， 修改后的超材料吸波体仿真结果如图12 所示， 从仿真结果中可以看出， 尽管结构发生了一些变化， 但同样展现了宽角度吸波特性. 实际制备过程中直流偏置线一端直接接在地板上， 另一端则需要单独接到每个单元的另一条直流偏置馈线上， 以实现对每个单元可变电容的调控. 但这样做会增加结构复杂度和控制复杂度. 因为本文的目的是验证方法的效果， 所以只使用了最简单的固定电容进行验证. 在应用需要时， 可以通过上述方法实现连续可调.

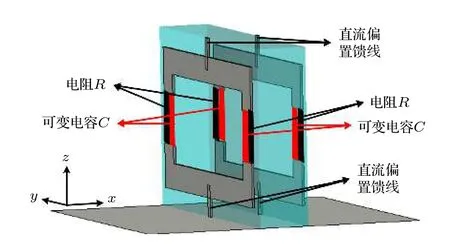
图11 频率可调超材料吸波结构Fig. 11. Frequency-tunable metamaterial absorber.

图12 频率可调超材料吸波结构不同电容值下的反射系数 (a) TE 波； (b) TM 波Fig. 12. Reflection coefficient of frequency-tunable metamaterial absorber with different capacitance capacitors： (a) TE wave； (b) TM wave.

4 结 论

本文基于等效介质原理， 设计了一种双面开口谐振环结构的宽角度超材料吸波体， 引入集总电阻R调控等效磁导率， 引入集总电容C调控谐振频率， 电容和电阻则均加载在开口谐振环的开口处. 仿真和实测结果显示当TE 波照射时， 电阻R=4000 Ω，C= 1.5 pF， 在1.59 GHz 处实现了70°内90%以上的吸波率以及75°内85%以上的吸波率， 当TM 波照射时电阻R= 1200 Ω，C= 1.5 pF，在1.59 GHz 处同样实现了70°内90%以上的吸波率以及75°内85%以上的吸波率， 并且与基于等效介质原理的理论分析结果基本符合. 尽管由于加工的误差出现了细微的频偏， 但测试结果基本与仿真结果符合， 样品仍然具有宽角度的吸收特性. 本文设计的超材料吸波体还具有中心频率稳定性， 随着入射角度的增加， 其中心工作频率几乎不发生偏移. 此外， 当加载的电容C发生变化而结构的其他参数和电阻R不发生变化时， 超材料吸波体在新的吸收频率处仍然有同样的宽角度吸波效果， 具有宽频带的工作特性.