基于时间序列分析的滑坡位移预测
——以尖山营古滑坡复活为例
邱 茂,董建辉,赵建军,谢飞鸿,朱要强,邹银先
(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059;2.成都大学建筑与土木工程学院,成都 610106;3.四川大学水利水电学院,成都 610065;4.贵州省地质环境监测院,贵阳 550000)
滑坡变形的预测预报一直以来都是研究的重难点。为攻克这一难题,自20世纪60年代以来,学者们相继提出了各种预测预报方法。许强等[1-2]通过大量的研究,将这些方法分为定性、定量及两者结合的预测预报方法;徐峰等[3]利用灰色模型与自回归模型组合,对八字门滑坡位移进行了预测;陈亮青等[4]以结合平均影响值法与广义回归神经网络建立组合模型,预测了树坪滑坡位移,准确度较高;杨背背等[5]建立了一种长短时记忆网络预测模型,与支持向量机预测结果进行了对比,分析得出其精确度高于支持向量机模型;黄赠等[6]在地理信息系统的基础上,结合神经网络算法,对地震滑坡易发性进行了预测;张鹏等[7]通过小波变换修正了自回归滑动平均(ARMA)模型误差,预测了某堤坝水平位移;雷德鑫等[8]使用整合滑动平均自回归(ARIMA)模型预测了王家坡滑坡位移。孙光林[9]使用ARMA模型对南芬露天铁矿一滑坡动力变化进行了预测,取得了较好的效果;邓洪高等[10]利用马尔科夫链对灰色模型进行了改进,在对滑坡位移预测中误差比原灰色模型明显减小;Miao等[11]利用支持向量回归机(SVR)模型对阶跃型滑坡位移进行了预测;Tan等[12]利用灰色理论方法,分析了滑坡在各个变形阶段的主要影响因素。
滑坡位移的时间序列模型由趋势项、周期项、季节项、随机项组成,对各位移分量进行预测,叠加得到总位移。滑坡位移的预测模型众多,然而,每一种预测模型针对不同情况皆存在一定的缺陷,模型的复杂性实际并不决定其预测准确性,需要结合具体的工程情况选择适宜的模型才能得到更好的预测效果。陈明东等[13]最早在新滩滑坡位移预测验证上采用了灰色(1,1)模型[GM(1,1)];夏元友[14]使用改进的灰色GM(1,N)模型对滑坡位移进行预测,研究证明了其模型具备较高的可信度;李秀珍等[15-16]也使用灰色GM(1,1)模型进行滑坡预测,取得了较好的效果。可见灰色GM模型在滑坡预测方面是具备较强的适用性的。
当前对于古滑坡位移预测的研究较少。为此,基于时间序列分析,在深入探究尖山营古滑坡复活位移特征及诱因的基础上,将滑坡地表位移分解为受自身地质条件演化控制的趋势项和外界降雨影响的周期项。使用等维新息灰色模型预测趋势项位移分量,再以自回归模型对周期项位移分量进行预测。将两项预测结果叠加以求得总位移预测值。
1 滑坡位移时间序列分析
1.1 时间序列的分解
尖山营古滑坡的位移产生,是由于其下部煤层开采后滑坡本身的演化规律和降雨共同作用所导致。对于滑坡位移的时间序列,可以分解为由滑坡自身演变控制的趋势项位移和降雨影响的周期项位移。根据现场调查情况以及监测资料,排除了监测位移值时间序列中的人类活动随机项和季节项,滑坡位移时间序列加法模型为
y(t)=T(t)+C(t)
(1)
式(1)中:y(t)为位移时间序列;T(t)为趋势项位移分量函数;C(t)为周期项位移分量函数。
1.2 滑坡位移预测模型
灰色模型理论的基本原理是利用系统已有的数据信息,建立白化方程,从而预测系统发展规律。GM(1,1)模型的累加灰生成及白化方程,决定了它无法分析原序列的周期性,但是能较好的描述原序列的趋势性。因此,对于滑坡位移的趋势项位移分量,利用等维新息GM(1,1)灰色模型进行预测。等维新息灰色模型,是在原GM(1,1)灰色模型的基础上,根据新信息优先原则,通过原数据序列预测得到下一个数据后,添加到原数据序列,并剔除原数据序列的第一个数据,使数据序列保持等维,再进行下一个数据预测。
在得到趋势项预测值后,用总位移值减去趋势项预测值,即可得到周期项位移分量。在滑坡周期项位移分量的处理上,使用ARIMA模型、ARMA模型或AR模型还需结合时序的自相关、偏自相关图像来决定。将趋势项位移预测值与周期项位移预测值相加即可得到总位移预测值。
2 尖山营古滑坡
2.1 滑坡概况
尖山营古滑坡位于贵州省六盘水市水城县内,滑坡区域自然坡度为25°~45°,后缘高程1 400 m,坡脚高程1 310 m。煤系地层出露标高900~1 300 m。滑坡平面呈簸箕状,纵长150 m,横宽 180 m,平均厚度18 m,主滑方向45°,面积2.7×104m2,总体积48.6×104m3,如图1所示。

图1 滑坡全貌图Fig.1 General view of landslide
尖山营古滑坡为土质滑坡。滑体可分为上下两层,上层为黄色崩坡积土,厚度较薄,约4 m;下层为紫红色残坡积土,厚14 m。下覆基岩为二叠系上统龙潭组粉砂质泥岩、三叠系下统飞仙关组粉砂岩,岩层产状180°∠15°,如图2所示。

图2 滑坡剖面图Fig.2 Landslide profile
根据现场地质调查资料分析,将监测点布置在古滑坡坡体中下部,其主要为监测地表位移变化情况,对GPS01的监`测数据进行重点分析和研究,如图3所示。

LF1~LF4为裂缝编号图3 滑坡工程地质平面图Fig.3 Engineering geology plan of landslide
2.2 监测数据分析
以尖山营古滑坡2019年4月10日—7月31日的每日位移量、位移速率及日降雨量监测数据进行分析。滑坡位移、位移速率与降雨量关系如图4、图5所示。
由图4、图5可知,尖山营古滑坡位移变形表现为初始变形、加速变形、减速变形3个阶段。2019年5月底尖山营地区进入雨季,雨量充沛,日降雨量峰值在5月24日达到38.7 mm;2019年7月累计降雨最高达到90 mm。短期内较大降雨均对滑坡位移产生了一定影响。2019年4月10日—7月31日滑坡累计位移达4 430.5 mm。
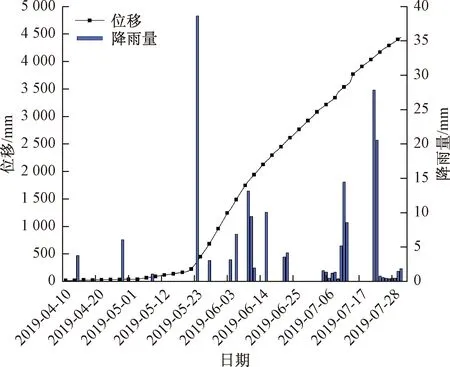
图4 滑坡累计位移量与降雨量关系Fig.4 Relationship between cumulative landslide displacement and rainfall
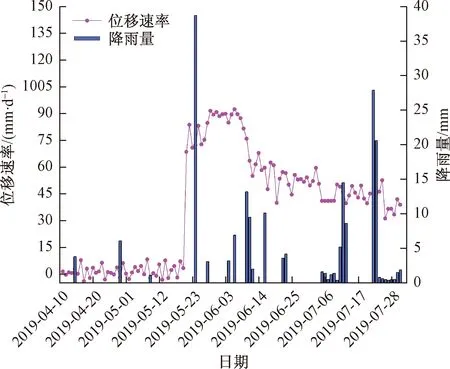
图5 滑坡位移速率与降雨量关系Fig.5 Relationship between landslide displacement rate and rainfall
2019年4月10日—5月20日尖山营古滑坡处于初始变形阶段,位移呈缓慢增长趋势,累计位移73.7 mm。位移速率较小,在10 mm/d以下周期性波动。此时尖山营古滑坡下部煤层采空后上覆岩层还具有一定的支护作用,岩土体中产生的裂隙还未完全发育,且所处地区尚未进入雨季,雨量较小,未对滑坡产生较大影响。因此,滑坡表面位移监测数据尚未有较大变化。
2019年5月20日—6月9日尖山营古滑坡处于加速变形阶段。由于采空区顶板塌落,上部覆岩移动变形,失去支护能力,导致滑坡位移速率发生较大的变化,位移陡增,6月9日达到1 747.8 mm。在5月21日位移发生阶跃后,从5月22日—5月27日监测数据来看,滑坡位移速率进入周期性上下波动的状态。5月24日降雨量达38.7 mm,滑坡受到下部煤层采动的影响,内部产生了大量裂隙,雨水经过一定时间由地表渗入坡体内部裂隙,加剧了滑坡变形,导致5月29日本处于周期性波动的滑坡位移速率再次陡增,达到91.4 mm/d。
滑坡及下部岩层在受到采动影响发生变形后,应力重分布,逐渐开始建立新的平衡。6月9日后滑坡进入减速变形阶段,滑坡的位移速率仍然呈周期性波动,整体上呈下降趋势。6月10日—6月12日、16日,7月5日—7月13日、7月22日—7月23日的降雨,都导致了滑坡位移速率明显增加,降雨对滑坡位移的影响表现出一定的滞后性。
综合以上对滑坡位移、位移速率及降雨量的分析,可知滑坡位移的主要是由煤层采动后引起的一系列地质条件演化及降雨的影响。其中煤层采动引起的滑坡自身地质条件的演化对滑坡位移具有明显的趋势性主导作用,而降雨则对滑坡位移速率的周期性变化有较大影响,两者的共同作用,导致了滑坡产生变形。
3 滑坡位移预测
尖山营古滑坡位移主要受自身地质状况的演变及降雨因素的综合影响,由趋势项与周期项组合相加形成总位移。现以尖山营古滑坡2019年4月10日—7月21日位移监测数据为原始序列,以7月22日—7月31日监测数据为预测检验样本进行预测。
3.1 趋势项预测分析
对于趋势项预测采用等维新息灰色模型进行预测,灰色GM(1,1)模型建立流程如图6所示。
等维新息灰色模型就是在得到一个预测值后,将预测值加入原序列,再去掉原序列第一个值,保持模型等维,进行下一次预测。等维新息GM(1,1)灰色模型趋势项预测曲线如图7所示。

a为灰发展系数;b为灰作用量图6 GM(1,1)模型建立流程Fig.6 GM (1,1) model establishment process

图7 趋势项预测值与实测值对比Fig.7 Comparison of predicted and measured trend values
由于等维新息灰色模型无法考虑原时间序列周期项,所以实际曲线与预测曲线存在一定误差。从图7可以看出,预测值在实测值上下呈周期性波动,通过式(2)计算相对误差:

(2)
式(2)中:δ为相对误差;d为绝对误差;M为实测值。
经计算,各点相对误差均在15%以内,平均相对误差为3.5%,误差来源主要表现在从5月底进入雨季后,降雨改变了滑坡原本位移的趋势,每次降雨导致位移速率抬升,降雨影响结束后位移速率再回归本身趋势,从而形成了预测曲线与实测曲线的周期性误差。
3.2 周期项预测分析
对周期项位移分量的分离,用总位移减去趋势项预测值,即可得到。对周期项位移分量,通过单位根检验后,判断周期项位移分量时序为平稳时序,即可进行建模。模型的选择以及定阶,由周期项位移分量时间序列的自相关图(ACF)和偏自相关图(PACF)的拖尾性、截尾性来判别。ACF和PACF分别如图8、图9所示。
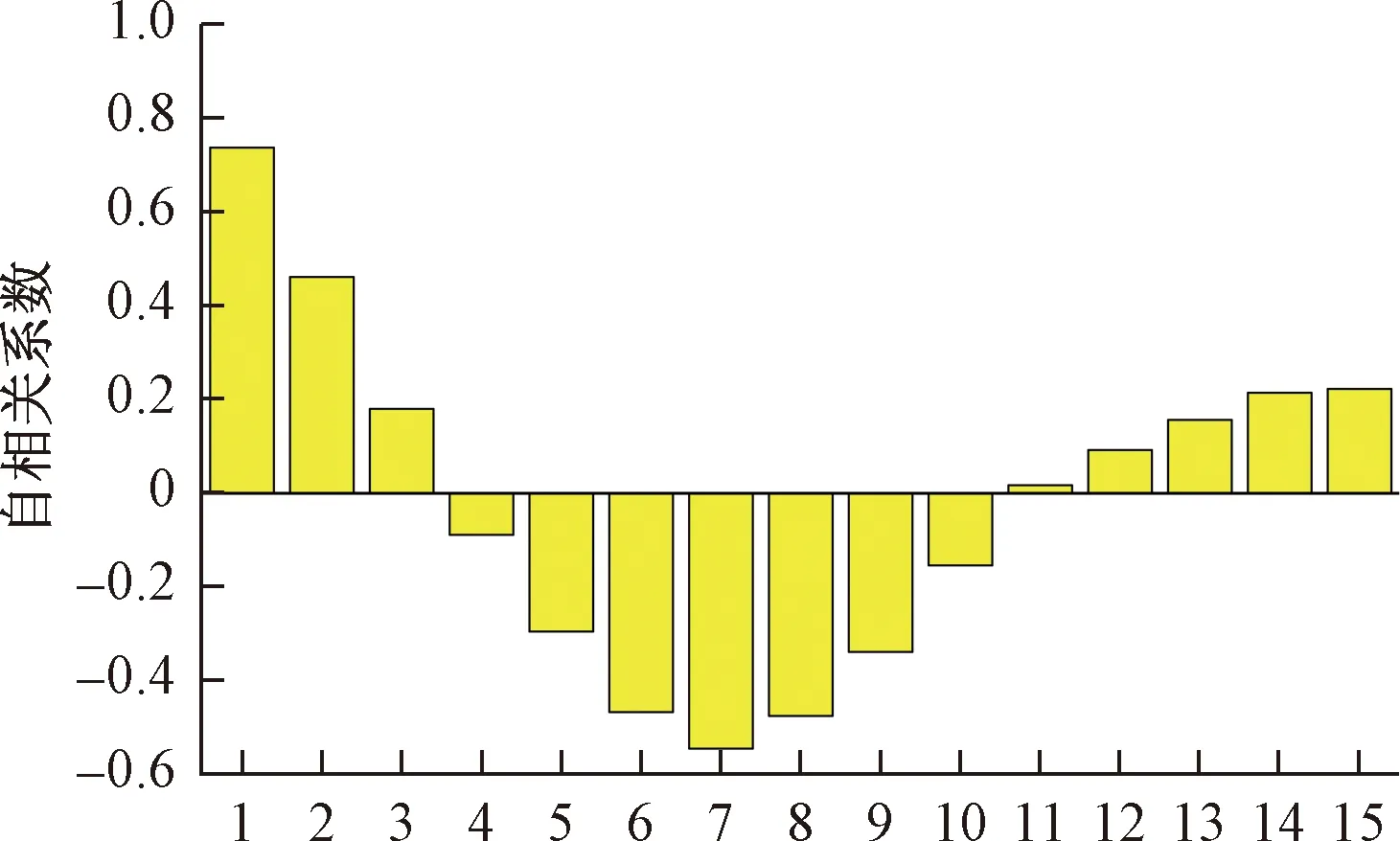
图8 周期项位移自相关性柱状图Fig.8 Histogram of periodic term displacement autocorrelation

图9 周期项位移偏自相关性柱状图Fig.9 Histogram of periodic term displacement partial autocorrelation
截尾性指自相关或偏自相关柱状图中的值自某阶后突变为0;拖尾性指自相关或偏自相关柱状图中的值自某阶后进入衰减趋势,但未直接衰减至0。由图8、图9可知,周期项位移时序自相关拖尾,偏自相关截尾,符合自回归(AR)模型建模条件。偏自相关柱状图1阶截尾,因此AR模型阶数为1阶。采用AR模型进行分析预测,AR模型表达式为
xt=φ1xt-1+φ2xt-2+…+φpxt-p+at
(3)
式(3)中:xt为预测值,φ1、φ2、φp为自回归系数;at为均值为0的白噪声序列。
将所提取的周期项位移分量代入计算,得到周期性位移分量预测值与提取值对比曲线,如图10所示。从图10中可以看出,AR模型对于滑坡位移的周期项提取序列具有较好的修正作用,周期残差有所降低。
3.3 总位移预测
将AR模型预测的周期项位移分量与GM(1,1)模型预测的趋势项位移分量叠加,即可得到总位移预测曲线,如图11所示。
从图11可以看出,经过AR模型修正周期项位移分量后,预测曲线与实测曲线更加吻合了。经计算,平均相对误差从3.5%降到3.2%。误差较大的四点对应日期为5月22日、6月2日、6月17日、7月16日。5月22日误差主要是由于滑坡刚进入加速变形阶段,其位移速率增量太大,预测模型难以拟合。6月2日、6月17日、7月16日的误差主要是由于降雨导致滑坡位移增加,并具有一定的滞后性。总的来说,模型精度较高,能满足实际应用。

图11 总位移实测值及预测值Fig.11 Measured and predicted total displacement
4 结论
使用GM(1,1)灰色模型、AR模型组合对尖山营古滑坡位移进行预测,得出如下结论。
(1)降雨强度与滑坡所处的地质状况演化是导致尖山营古滑坡位移增加的主要因素。在滑坡位移速率增加较慢或者处于减速状态时,降雨的作用会导致滑坡位移速率出现周期性波动。
(2)将滑坡位移分解成了趋势项和周期项,采用等维新息GM(1,1)灰色模型预测趋势项,自回归AR模型预测周期项。对于滑坡位移进行分解预测的效果较好。
(3)滑坡自身演化和降雨对滑坡位移的滞后性影响会导致预测结果出现误差,对于这种误差的消除还需要进一步的研究。
(4)尖山营古滑坡由煤层采动引发的复活,位移的变化与其下部岩层变形机制密切相关,表现出强烈的趋势性。研究分析方法对于该类古滑坡的复活位移预测具有一定参考价值。

