融通算术教学 发展代数思维

○夏小进

运算教学在小学数学教学中占有重要地位。运算遵循一定的法则，按照一定的步骤，经历较长时间的数量加工与操作求得答案，这个过程是程序性的，体现的是算术思维。而代数思维是由关系或结构来描述的，它的目的是发现（一般化的）关系，明确结构，并把它们连接起来，是表征和分析数量关系、解决问题、陈述和证明一般规律的有效途径。

尽管《义务教育数学课程标准（2011年版）》已将“数与代数”设置为独立的学习领域，并对小学代数课程内容进行了清晰的表述，但算术和代数之间的一致性和整体性仍未尽如人意。如何在算术教学中培养学生的代数思维，实现算术教学与代数教学的有效衔接与融通？这是小学数学教学必须正视、思考和解决的问题。我们可以从以下几个方面展开思考。

一、在观察中感悟代数思维的结构性

小学算术中蕴含着不少代数思维的素材，在低年级就可以适时向学生渗透一定形式和层次的代数思维。教师要引导学生用代数的眼光观察算术问题，关注算术中的结构，思考、识别、提取包含于其中的关系，感受其中结构的变换和表达。

例如下面这道题，在□里填上合适的数。

以第一个算式为例，有两种思考方法：第一种方法是先计算等号左边，再依据“除数=被除数÷商”算出右边方框里的数，体现了算术思维的程序性；第二种方法则从整体上观察分析，36缩小4倍后是9，要想得数相等，右边方框里的数应该是24缩小4倍后的结果，从而快速得出答案6，避免了繁琐的计算，体现了代数思维的结构性。

这道题根据“商不变”“和不变”“差不变”“积不变”规律，引导学生从对数量的加工与操作转向对算式结构的探讨，从算术练习转向了代数学习，提升了思维水平，并能有效推动后续学习，如分数的约分、比的化简等。

二、在探寻中体悟代数推理的实用性

代数推理要求较高的抽象思维能力和演绎论证能力，具有丰富的思维训练价值，有助于培养学生思维的严谨性，促进小学生从具体形象思维向抽象逻辑思维过渡。小学高年级算术教学可以提供适当的机会，引导学生用代数的思维思考算术问题，探寻蕴藏其中的代数关系和结构。

例如，在学习与倍数相关的内容时，呈现下列算式，要求学生先笔算。

教师可以设计如下的教学流程——

小结：学生算完后总结这些数都是4的倍数。

提问：仔细观察这些数，它们有什么共同之处？

预设：这些数的末两位都是4的倍数。

猜想：一个数的末两位是4的倍数，那这个数本身也一定是4的倍数。

启发：你能证明这一猜想吗？

验证：两位以上的自然数，我们都可以用（100x+ab）来表示，其中ab就是它的末两位，因为100是4的倍数，所以100x也一定是4的倍数，如果ab是4的倍数，那么它们的和（100x+ab）也一定是4的倍数。

这种规律的探寻过程既有合情推理，又有初步的演绎推理。学生在观察、猜想、归纳、证明的过程中不仅获得了数学知识，发展了代数推理能力，也培养了严谨的理性精神和科学态度。

三、在分析中领悟代数表达的多样性

代数知识可被展示为言语表征、直观表征（动作、实物和图画等）、符号表征等多种形式，每种表征都反映了某一方面的特征。借助多元表征有利于学生从多角度展开数学探索，既丰富了对数学的理解，又丰富了问题解决的策略。教师应创造机会引导学生用代数的语言从多角度表达算术问题，培养代数思维，发展学生的思维能力。

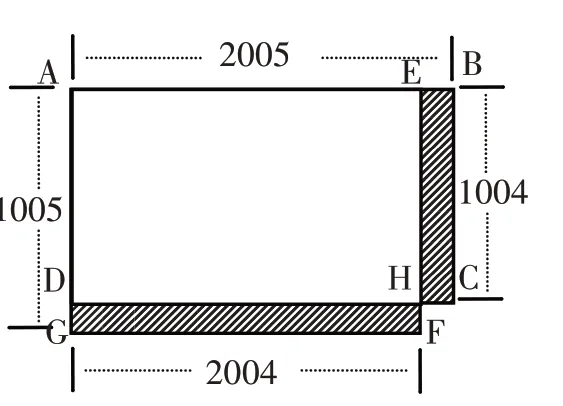
例如，计算：1005×2004-1004×2005。

由于直接计算特别繁琐，教师可以引导学生从整体上观察这个算式，尝试从多角度分析、表征算式的结构，发展代数思维，加强数学理解。

表征一：字母符号表征

表征二：图形表征

把1005×2004表征为长方形AEFG的面积，1004×2005表征为长方形ABCD的面积。于是原式就被表征为求长方形AEFG与长方形ABCD的面积之差，也就是求长方形DHFG与长方形EBCH的面积之差，容易看出长方形DHFG与长方形EBCH的 宽 都 是1，所以两者之差为：2004×1-1004×1=1000。

四、在对比中体会代数方法的优越性

算术方法是设法通过已知量求出未知量，在此过程中未知量被置于特殊地位，学生是逆向思维解题。如果题干中有多条信息且彼此存在复杂关系时，学生难免会产生一些困惑，从而产生解题障碍；而用代数方法解题属于顺向思维，先用字母代替未知数，等于增加了一项条件，未知量和已知量均参与运算，这就可以顺利建立等量关系。随着学习的深入，问题难度逐渐加深，代数方法的优势越发明显。教学中应加强学生对代数方法的学习、理解与运用，使学生意识到算术方法的局限性，从而自发产生代数学习的动力和兴趣。

例如，这道题：某工厂生产A、B两种商品，生产的A商品比B商品少12件。已知B商品全部合格，而A商品只有合格，两种商品合格的共有57件，两种商品各生产了多少件？

用算术方法解决这个问题需要较多的逆向思考和较复杂的解题技巧；而用代数方法（方程）可以根据题意正向建立等量关系式：合格的A商品数+合格的B商品数=57件。设生产A商品x件，则生产B商品（x+12）件，列方程为=57。从而简化解题过程，顺利解出答案。

综上，教师应引导学生意识到代数思维的优越性，让代数思维方式成为学生的内在需要，促进学生从算术思维向代数思维的跨越，为小学和初中数学学习内容的有效衔接搭建桥梁。