基于多智能体的图优化SLAM构建方法

宋燕燕，秦 军,2，邢艳芳，汪晨曦，周洪萍

(1.中国传媒大学南广学院，江苏 南京 211172； 2.南京邮电大学，江苏 南京 210003)

0 引 言

增强现实(augmented reality，AR)是一种结合虚拟化技术观察世界的方式，它利用计算机技术，将虚拟的物体实时地叠加到一个真实画面或空间，形成具有实时交互的三维图像画面，给用户带来更真实的体验与感受[1]。增强现实由于其在真实环境和虚拟环境中起到了一个连续体的作用，为相关的应用提供了一种新的人机交互方式，满足用户在现实世界中真实地感受虚拟空间中模拟的事物，增强使用的趣味性和互动性。近年来，随着同步定位与地图构建(SLAM)算法的不断更新，已经成为一个研究热点问题，定位(运动追踪)和建图(稀疏或者稠密地图)构成了SLAM的核心功能。因此，SLAM可以说是AR中最基础的模块，属于设备感知周边环境的范畴[2-4]。

在目前的研究中，SLAM一方面充分利用图像信息来提取图像特征，另一方面也通过融合深度相机、IMU等传感器满足视觉SLAM在困难条件时，仍然可以稳健定位建图的需要，在机器人自动化、智能化区域发挥着很重要的作用。在针对多机器人基于深度学习的SLAM算法中，国外学者提出了基于稀疏编码的迁移学习SLAM算法，这样就可以有效减小训练模型的数据量，并对模型的通用化进行了完善，使人们可以理解不同类型的数据，进而更好地对底层进行规划。在目前的研究中，对于避障问题，学者提出将导航策略转变为一个深度的神经网络，将障碍物信息设为输入量，速度控制信号设为输出量，通过大量数据训练模型，从而完成避障。异构多机器人搭载多种传感器相对于单一种类机器人具有更大的优势，基于多传感器数据融合SLAM的研究在搭载多机器人时可以更加有效地对复杂环境进行全面的地图构建[5-6]。

1 基于图优化的SLAM框架

视觉SLAM就是一个带有特定相机的承载主体，它可以在没有任何的提前探测的情况下，对自己接下来的路径进行规划。前端主要涉及到计算机视觉领域的问题，而后端主要与优化算法有关。

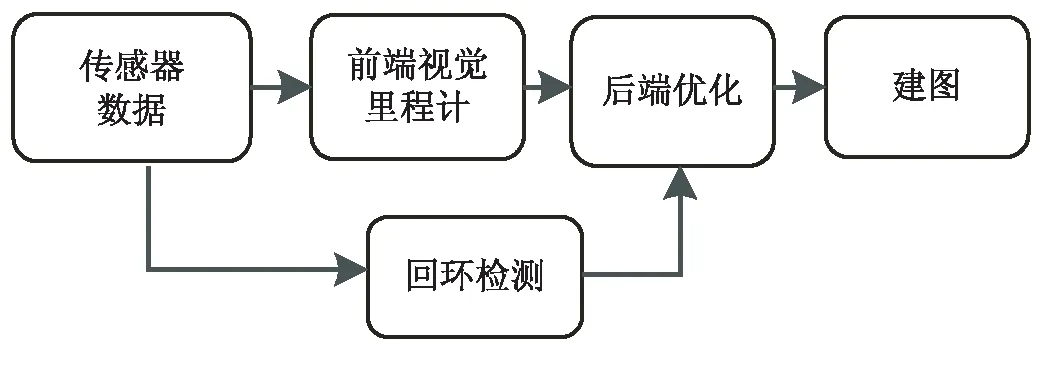
图1 整体视觉SLAM流程

整个视觉SLAM框架如图1所示，主要包含五个步骤：传感器信息读取、视觉里程计、后端优化、回环检测、建图。图优化是把常规的优化问题采用图的方式来表示，图优化中的图就是数据结构里的图，一个图由若干个顶点以及连接着这些顶点的边组成，如图2所示，可以更直观地看到其结构。

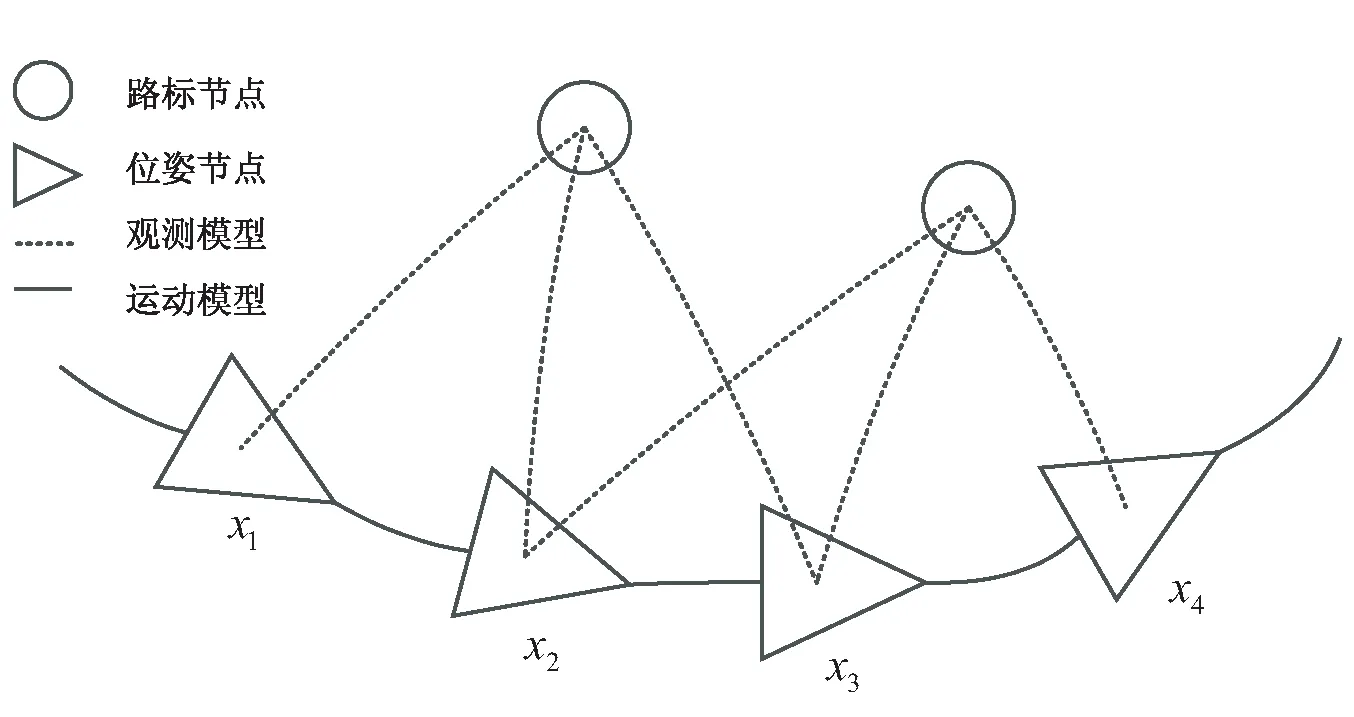
图2 图优化例子

图优化SLAM方法是先通过前端的图构建得到初始状态估计值，在前端得到初始地图[7-8]。但由于传感器的噪声等，使得最后所得到的结果具有较大的误差，需要通过后端对初始状态进行估计来进一步优化求解，使得地图的一致性和精度都得以提高。基于图优化的方法利用了这些信息来优化完整的地图路径，也称为全SLAM方法，如图3所示。

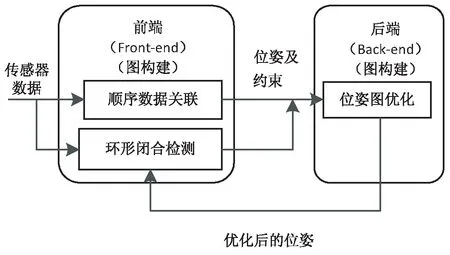
图3 基于图优化的SLAM框架

2 SLAM相机位姿的估计和优化

(1)

当对一个旋转矩阵R2(李代数为φ2)左乘一个微小旋转矩阵R1(李代数为φ1时，可以近似地看作在原有的李代数上加上了一项J1(φ2)-1φ1。在给近似添加了一个微小扰动的情况下,分成了左乘扰动和右乘扰动两种扰动方式。在使用时，须注意使用的是左乘模型还是右乘模型。

左乘BCH近似雅克比Jl为：

(2)

它的逆为：

(3)

而右乘雅克比只需要将右乘中的自变量取负号即可得到：

Jr(φ)=Jl(-φ)

(4)

为了讨论位姿的导数，会引入构建位姿函数调整当前的值，以调整整体的估计值，使用李代数表示位姿，来对其进行求导，再对左乘或者右乘进行扰动，最后对其求导。这时把结果称为左扰动和右扰动模型。

3 非线性优化SLAM问题

即使相机的运动方程可以很好地符合针孔模型，但由于噪声的存在，数据依旧会受到很大的影响，运动方程和观测方程会对测量结果有偏差。所以需要在有噪声的数据中进行准确的状态估计，从噪声数据中恢复出所需要的东西，优化处理噪声数据[11]。

3.1 状态估计问题

SLAM模型一般由两个方程——运动方程和观测方程组成：

(5)

观测方程在SLAM中具有特殊性，所以当在xk对yj进行观测，对应到图像中的像素位置zk,j,那么，便可得出观测方程：

szk,j=Kexp(ξ∧)yi

(6)

其中，s表示像素点之间的距离，k表示相机的内参。

在运动和观测设有的两个噪声项wk,vk,j满足以下条件：

wk～N(0,Rk),vk,j～N(0,Qk,j)

(7)

在噪声的干扰下，希望能够准确地计算出相机的位姿以及得到完整的地图(算出它们在有噪声的条件下的概率分布)。目前是采用非线性优化来解决这一状态估计问题，对每个时刻的数据中的噪点进行采集，然后对它进行状态估计。了解每个时刻中的误差点，这种方法已经成为了目前解决视觉SLAM中噪声问题的主要方法。在这里，把所有待估的变量放在一起：

x={x1,…,xn,y1,…,yn}

所以可得到x的条件概率分布：P(x|z,u)，在没有先验的情况下，没有告知刚体的运动方向，只有由像素点构成的图片时，就没有运动方程带来的具体数据，这样就只能依靠观测方程所产生的数据来判断，不必考虑在时间上的顺序。这时只能分析空间上物体的运动来得到三维结构信息，通过找到三维空物体图像的对应点(在图像中找到角点特征)，来恢复立体图像结构问题，这种方法被称为运动恢复结构SFM(structure from motion)。为了进一步了解此时的条件分布特征，利用贝叶斯法则，可以得到:

(8)

其中，P(x)为先验。很难找到后验分布，因此需要先求解该状态下的最优估计。使得在该状态下后验概率最大化(maximize a posterior，MAP)：

(9)

可以直接忽略贝叶斯法则的分母部分(与状态值x无关)。当无法判断刚体的位姿在什么地方时，就说明不能准确地得到先验概率。那么，此时可以求解x的最大似然估计:

(10)

似然是指在当前的情况下可能得到的数据，所以最大似然估计的直接意义就是“在什么样的状态下，最有可能产生的现在观测到的数据”。

观测方程中，只有在xi点可以看到yi时，才会产生观测数据。由于视觉SLAM的特征点非常多，所以在实际中观测方程的量会远大于运动方程。如果认定没有运动方程，整个优化问题就只能由多个观测方程得到，相当于通过一组图像来恢复运动的结构。这就比较类似于SFM，但SLAM中的图像有时间上的先后顺序，而SFM允许使用完全无关的图像。

3.2 非线性优化方案

非线性优化最常见的两种方案是高斯牛顿法和列文伯格—马夸尔特方法。由于目标函数复杂，对问题提供不同的初始值都容易陷入局部最小值，所以使用高斯牛顿法和列文伯格-马夸尔特法优化初始值。

3.2.1 高斯牛顿法

高斯牛顿法将f(x)进行一阶的泰勒展开：

f(x+Δx)≈f(x)+J(x)Δx

(J(x)为f(x)的导数)

(11)

它的目标是寻找下降矢量Δx,使得‖f(x+Δx)‖2达到最小，所以求解线性最小二乘：

(12)

将目标函数对Δx求导，并令导数为零，可得：

J(x)TJ(x)Δx=-J(x)Tf(x)

(13)

求解的变量为Δx，一般称为增量方程或者高斯牛顿方程(Gauss Newton equation)。将左边的系数项设为H，右边定义为g：

HΔx=g

(14)

将JTJ作为二阶Hessian矩阵的近似，省略掉了计算H的过程。所以可得高斯牛顿法的步骤为：

(1)给定初始值x0。

(2)对第k次迭代，求出当前的雅克比矩阵J(xk)和误差f(xk)。

(3)求解增量方程HΔx=g。

(4)直到Δxk足够小，则停止。否则，令xk+1=xk+Δxk，继续第二步。

从算法中可以看出，增量方程求解占据主要位置。它要求所用的近似H矩阵是可逆的(而且是正定的)。但是可能出现的JTJ却只有半正定性。在使用高斯牛顿法时，可能会出现JTJ为奇异矩阵或者病态的情况，导致算法不收敛。即使排除这一情况，在求步长Δx时，若它过大，也会使得局部近似不够准确，无法保证它的迭性收敛。

3.2.2 列文伯格-马夸尔特法

高斯牛顿法在运算时具有局限性，它只能展开附近较好的近似效果，因此需要给Δx添加信赖区域(trust region)来提高它的准确性。在非线性优化中，这类方法被称为信赖区域法(trust region method)。一般区域的大小与近似模型和实际函数的差异成反比，用ρ来代替两个函数的差异性:

(15)

其中，分子表示实际函数的下降值，分母表示近似模型的下降值。若ρ接近于1，则近似值是正好的；若ρ太小，则近似性比较差，需要缩小范围；反之，则说明实际下降范围比较大，这时，需要放大范围。

因此构建了一个改良的非线性优化框架，即：

(1)给定初始值x0以及优化半径μ。

(2)对于第k次迭代，可得：

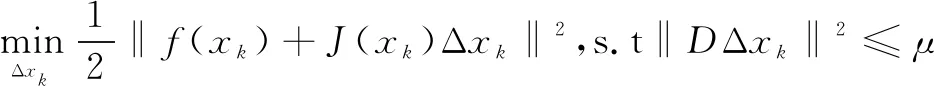
(3)计算ρ。

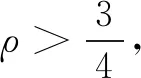
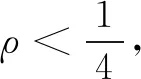
(6)ρ大于阈值，则认为近似可行，令xk+1=xk+Δxk。

(7)判断算法是否收敛，若不收敛，则继续第二步；否则结束。

马夸尔特提出将D取成非负数对角阵—通常用JTJ的对角元素平方根，这样使得在梯度维度上的约束范围会变得大一些。用拉格朗日乘子将它转化为一个无约束化问题：

(16)

可以发现计算增量的线性方程仍然是该问题的核心：

(H+λDTD)Δx=g(以下用I代替DTD)

(17)

在这个增量方程中，相比于高斯牛顿法，多了一项λI。当λ较小时，H占主要地位；另一个方面，当λ较大时，λI将占据主要地位。列文伯格—马夸尔特法为优化问题提供更稳定、准确的增量Δx，在一定程度上避免了方程组的非奇异性和病态问题。

4 多智能体与SLAM构建

多智能体技术可以为SLAM提供很好的稳定性和鲁棒性，使视觉SLAM得到更加有效可靠的特征。具有无监督学习机制的SLAM已经在现实应用中有很大的市场，将以上非线性优化方案结合多智能体技术使得实时追踪能够具有自身的协调能力，更好地应用于适应未来的市场发展机制[12-13]。视觉SLAM则是增强现实(AR)中一个很好的搭载辅助工具。它可以自主地识别空间中的墙壁，障碍物以及其他物品。当出现大规模的数据集时，基于数据的图优化SLAM能够自主提取特征，而非手动提取。但当出现大规模数据时，它的鲁棒性还需要进一步提升[14]。

基于深度学习图优化的SLAM也具有很强的灵活性，它不仅可以估计位置和构建三维点云地图，并且可以产生估计的不确定性，为后续的决策所服务[15]。但是它也存在误差很大，数据增长很快的情况。该文提供了一种解决方法：核函数。它能保证每条边的误差不会大到掩盖其他的边。把原先误差的二范数度量替换成一个增长没有那么快的函数，保证自己的光滑性质(否则无法求导)，使得整个优化过程更为稳健，所以又叫鲁棒核函数(robust kernel)。

鲁棒核函数最常用的Huber核为：

(18)

当误差e大于某个阈值δ时，函数增加由二次形式变成了一次形式，相当于限制了梯度的最大值。如图4所示，可见误差较大时Huber核函数增长明显低于二次函数。在生成场景语义图时，如何进一步提高改善定位性和鲁棒性还需不断探索，期待场景语义图可以帮助定位，并进一步减少数据存储量，从而有助于大规模大尺度环境构图。

图4 Huber核函数

通过该文构建的方法，将非线性优化方案结合多智能体进行SLAM构建，实现移动平台真实浏览虚拟样板间的可视化与交互，运动跟踪是通过识别和跟踪用户周围的可识别特征来完成的，然后利用这些点以及设备的朝向和加速度传感器来保持跟踪更新。如果没有这些信息，就无法实现准确跟踪。随后通过USB或远程将设备与开发机器相连，然后在设备上构建和运行应用程序。绘制点云数据需要花费一段时间。并且随着点的个数的增加，在一个方向保持设备的时间就越长。这些点表示用于跟踪和解释环境的可识别特征点。放置对象用光线投射技术，光线投射技术可在两个维度上获取触摸点，并向场景投射光线，然后该射线测试场景中产生碰撞的其他对象。检测到平面的效果如图5所示，图6为点击平面后叠加出现另一个虚拟样板间的效果。

图5 检测到平面

图6 点击平面并出现门

5 结束语

基于图优化SLAM算法与多智能体结合，提出一种构建方法，并对增强现实进行应用讨论。现在人工智能和增强现实技术在社会中的地位稳步上升，这些领域的核心关键技术在逐步实现突破，视觉识别技术也遥遥领先。图优化SLAM与多智能体的结合，给增强现实在构建完整地图提供了良好的开端，实现了SLAM与增强现实的结合。视觉SLAM系统在大尺度地图中的速度，优化算法能得到提升。在大环境下系统性将会变得脆弱，鲁棒性也随之降低。如果遇到特征点很少的场景、交叉的白平衡、图片失真等情况，这些给对特征检测增加很大的难题，数据会变大，导致无法很好地存储与处理地图。当将多智能体技术与其相结合，通过智能体之间的相互协调性提高算法的速度，通过智能体之间的相互通信实现对每一个零散的点进行整合，能得到一个更好的三维地图，在未来的自动驾驶等领域会得到良好的应用。