基于用户属性聚类与矩阵填充的景点推荐算法

刘荣权，袁仕芳，赵锦珍，杨伟杰

(五邑大学 数学与计算科学学院，广东 江门 529020)

0 引 言

在当今数据化时代，人们出行需要从海量景点信息中选取自己喜欢的景点，导致旅游用户出行前有选择困难。为了解决这个问题，许多旅游推荐系统会根据用户的行为特征，给用户推荐一些可能喜欢的景点，帮助用户做出选择。近几年来，基于用户的协同过滤算法和基于项目的协同过滤算法[1]在这方面起到了重要的作用。目前有很多学者不断改进传统的协同过滤算法，以提高旅游推荐的质量[2-4]。

传统协同过滤算法主要是根据评分矩阵计算推荐结果，评分矩阵的好坏直接影响推荐的质量。评分矩阵最大的不足是数据稀疏[5]，因为大部分用户去过的旅游景点数较少，只会对海量景点中的少数景点做出评分，从而做出的评分数量很少，使得评分矩阵出现大量的缺失值。

针对上述问题，该文尝试基于用户的属性对用户进行聚类，计算目标用户与同一类中的其他用户的相似度，这样不仅减少了计算量，而且使所得近邻用户集更准确。然后用奇异值分解算法填充评分矩阵，从而在计算预测评分时减少数据稀疏带来的影响，提高预测评分的准确性。

1 用户属性聚类

目前传统k-means算法[6]和二分k-means聚类算法[7]在用户属性聚类算法中有重要应用。传统k-means算法：随机选取初始簇心、无法确定类别个数造成聚类误差较大，文献[8]证明了二分k-means聚类减小初始随机选取簇心的影响,降低聚类误差。传统的推荐算法是在单一的评分矩阵中给目标用户推荐项目，如果数据过于稀疏，将导致目标用户的近邻用户集不准确。本节主要讨论将二分k-means聚类算法应用到用户属性聚类中，因为同一类用户的特征越相似，则它们的相似度越高，这使得目标用户的相近邻用户集越准确。

1.1 旅游用户属性预处理

用户属性是指用户的一些基本特征。在文献[9]中提到，影响用户出行的因素主要有职业、性别、年龄、出行时段、出游陪同、人均消费和出发天数。以文献[9]为基础，该文选取用户性别、注册年份、天数、出发时间、陪同、人均消费和玩法作为用户属性，构成数据集。对数据集进行量化，玩法量化主要计算每个用户的玩法的词频和与总玩法的词频和之比。量化如表1所示。

表1 用户属性量化

续表1

1.2 二分k-means聚类

定义用户集{xi|i=1,2,…,n}和用户属性集{aij|j=1,2,…,7}(例如用ai1可表示用户i的性别属性值，后面的以此类推)，对每一个用户属性集进行归一化处理，消除指标之间的量纲的影响，处理方法如下：

其中， max(aj)、min(aj)是用户属性j的最大值、最小值。

k-means聚类算法描述如下：

输入：用户属性集合，聚类数K。

输出：K个聚类结果。

(1)初始化K个聚类中心。在每个属性的范围内选择K个随机值，生成K个聚类中心，以保证每个聚类中心仍处于原数据集内。定义第i个聚类中心为：

ci={ci1,ci2,…,ci7},i∈{i|1≤i≤K,i∈N}

cij=[max(aj)-min(aj)]·rand+min(aj)

{j|1≤j≤7}

其中，rand是(0,1)之间的随机数，cij是聚类中心ci第j个用户属性的随机值。

(2)计算所有样本点到K个聚类中心的欧氏距离，并把样本点归类到距离最小的类中。计算公式如下：

d(xi,cj)=

其中，xi是第i个用户的用户属性向量，cj是第j类的聚类中心。

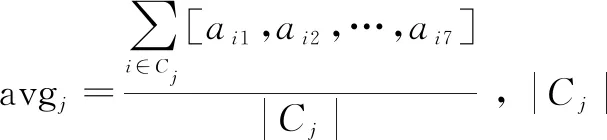
当聚类数K=2时，k-means算法变为二分k-means算法，它的主要聚类过程是k-means算法。算法一般采用误差平方和作为目标函数，不断迭代优化聚类结果，当目标函数收敛，迭代结束。目标函数如下：

其中，error为所有用户与对应聚类中心的误差平方和，ci为第i类的聚类中心，x为第i类的样本点。

二分k-means聚类算法描述如下：

输入：用户属性集合，聚类数K。

输出：K个聚类结果。

(1)初始时，建立类表(用于存储二分聚类结果)，将所有用户视为同一类c并存入类表。

(2)当类表中只有一类c时，将此类c中所有用户属性代入上述k-means聚类算法(K=2)，得到两个新类c1,c2，存入类表并取代c。

当类表中有两类及以上时，以聚类后所得误差平方和最小为目标，遍历当前类表中的所有类，执行上述k-means聚类算法；当遍历完毕时，若某类满足上述目标，使其成为目标类并执行二分聚类，将所得两个新类取代目标类。

(3)当K达到输入要求时，算法停止，否则继续执行步骤(2)。

2 景点推荐算法

上一节对用户属性进行二分k-means聚类，使同一类中的用户具有更高的相似度；在计算目标用户与同一类其他用户的相似度时，不仅减少了计算量，而且使所得近邻用户集更准确。但在实际中，用户之间共同评分的景点数较少，使评分矩阵稀疏程度偏大。本节采用文献[10]中的矩阵奇异值分解(SVD)对用户景点评分矩阵进行填补，并基于用户的协同过滤算法，预测目标用户景点评分。

2.1 传统的协同过滤算法

传统的协同过滤算法包括基于用户的协同过滤算法和基于项目的协同过滤算法[11]。由于大部分景点缺失描述信息，也没有相应描述标签，使景点之间的相似度不易计算。若采用基于项目的协同过滤算法进行推荐，则难以实施。因此该文采用基于用户的协同过滤算法。

它的主要内容如下：

(1)构建用户景点评分矩阵。

收集m个用户对n个景点的评分数据，定义用户集{x|x1,x2,…,xm}，景点集{y|y1,y2,…,yn}，构成大小m×n的评分矩阵，如图1所示。

图1 用户-景点评分矩阵

其中，S(xi,yj)为用户xi对景点yj的评分；规定用户未评价景点的评分为-1，依据用户对景点的喜爱程度，将评分设为五分制。

(2)用户相似度。

在推荐系统中，计算相似度的方法有Jaccard相关系数[12]、余弦相似度和Pearson相关系数等等[13]，其中Pearson相关系数应用较为广泛。该文使用Pearson相关系数计算用户相似度，公式如下：

(3)景点评分预测。

2.2 SVD算法填充矩阵

在推荐系统中，用户景点评分矩阵的数据稀疏性严重影响推荐算法的预测准确度。对于数据稀疏，文献[15]的解决办法有：简单的数据填补、对用户进行聚类和数据降维。

本节采用SVD算法[16]对原数据进行降维分解，最大程度地保留原数据的信息，填充原数据的缺失值，得到完整的评分矩阵。填充过程描述如下：

在Σm×n中，对角元素称为奇异值，它包含着R'中重要的信息，这也是数据降维的关键。

(2)规定阈值为95%。当前k个奇异值的累计贡献率达到95%，可认为这前k个奇异值保存足够的特征。

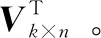
(5) 对缺失值进行预测。计算用户x在景点i缺失值的预测评分，可以通过下式求解：

2.3 总体的算法流程

算法实现流程如图2所示。

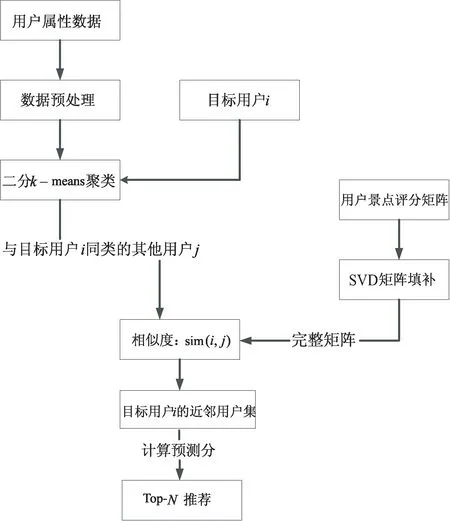
图2 算法实现流程

3 数据实验与分析

3.1 实验环境

实验环境为Windows7、64位操作系统，所用编程语言为Python。

3.2 实验数据

该研究在携程网站(www.ctrip.com)，以“深圳”为关键字，收集用户和评分数据。共获得1 551个用户数据以及用户对49个景点的评分数据。分析可知，评分矩阵的稀疏度为92.5%。随机选取80%的实验数据作为训练集，20%作为测试集。

3.3 评测指标

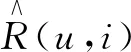
MAE的定义如下：

其中，|N|是未评分的景点数量。

3.4 实验结果与分析

初始时，二分k-means聚类数K是一个不确定值。以二分聚类结果的误差平方和最小为目标，循环运算二分k-means聚类算法得到最优的K值。从图3中可见，当聚类数为5时，误差平方和最小。综上该文选取聚类K=5。

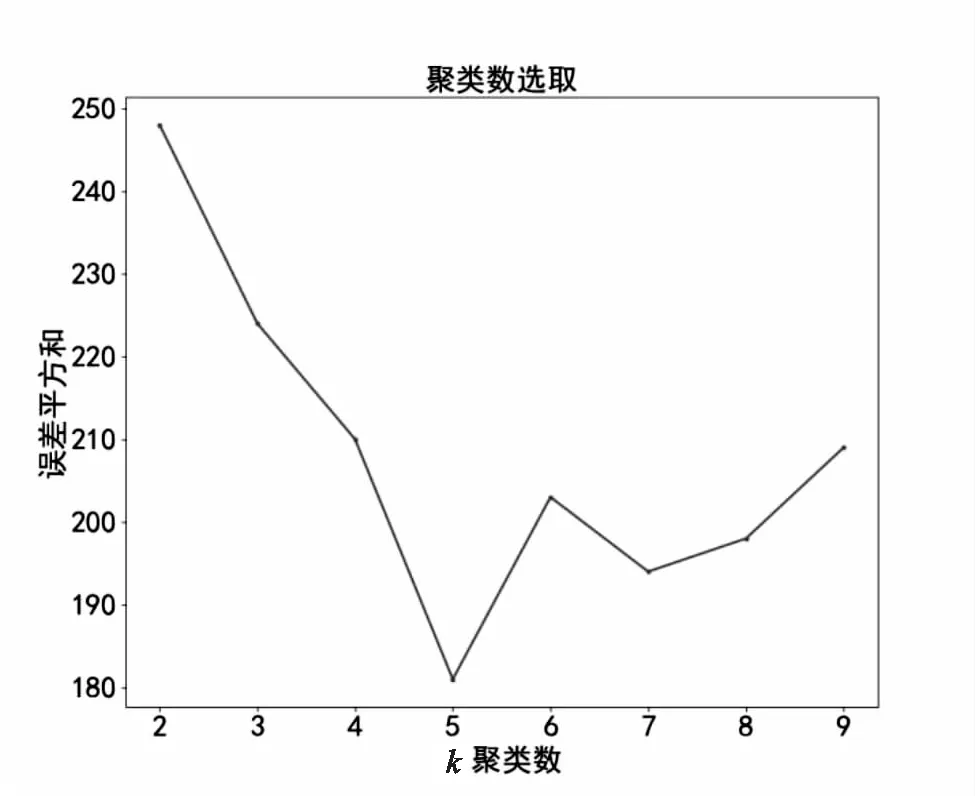
图3 最佳K聚类数

对于多维聚类，利用Python的TSNE进行数据可视化，将五维数据的聚类结果展示到二维空间，如图4所示。可见原数据聚类成五类，同一类中聚拢程度高，不同类间分界明显，聚类效果符合预期目标。

为了评测该算法的推荐质量，将基于用户的协同过滤算法、经聚类优化后的协同过滤算法与文中算法进行比较。三个算法在不同的近邻用户数量下，计算MAE并比较，结果如图5所示。

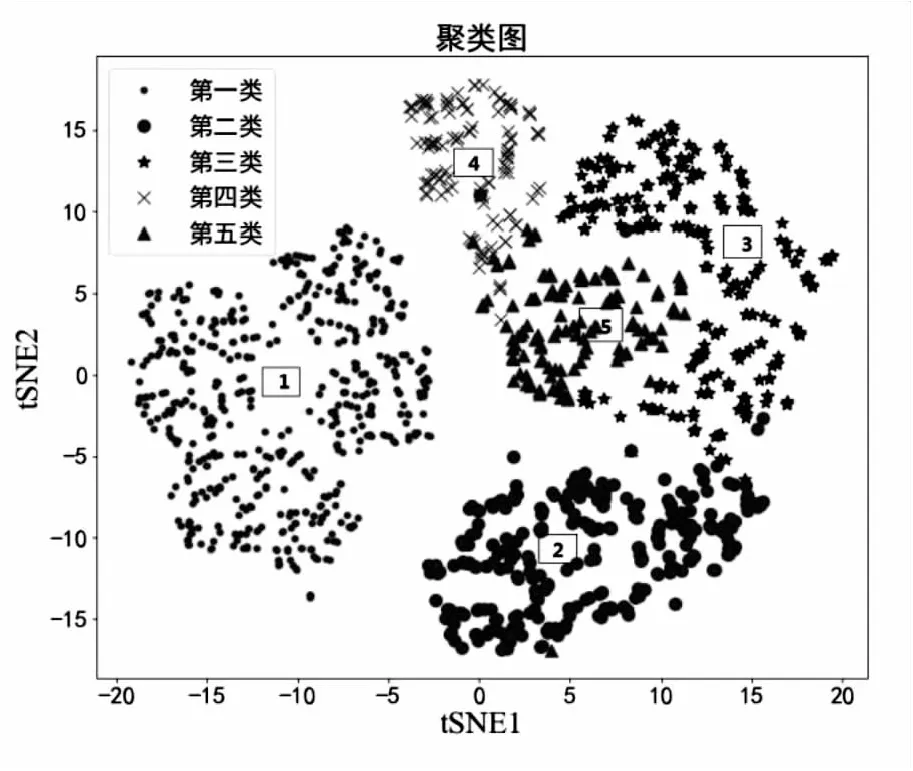
图4 聚类结果可视化

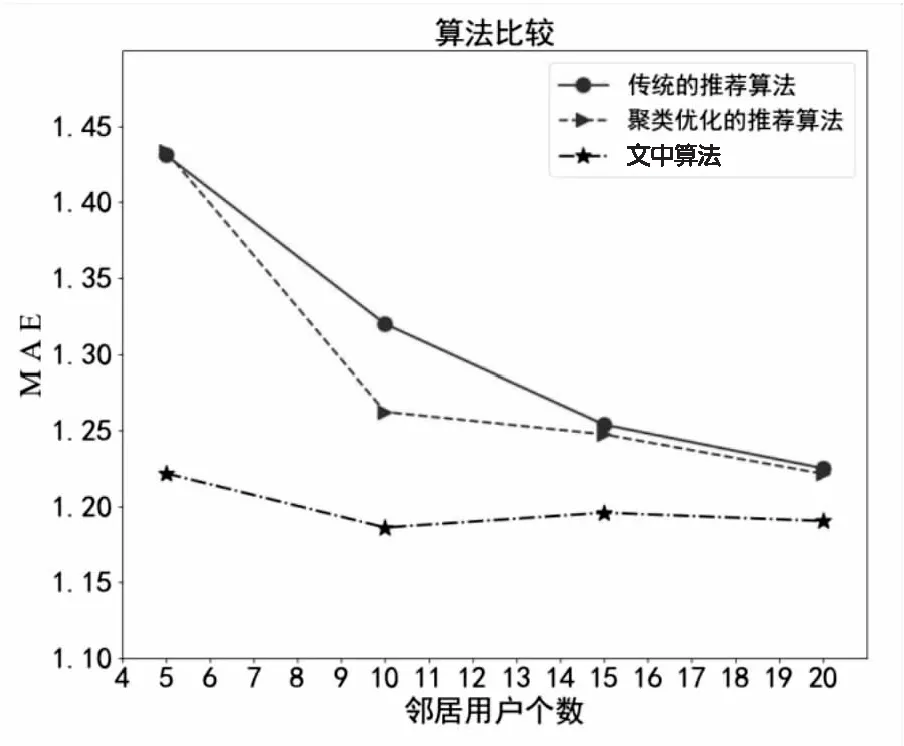
图5 不同算法比较

由图5可知，在不同的近邻用户数量下，文中算法所得MAE值均比基于用户的协同过滤算法、聚类后的协同过滤算法的小，说明文中算法的景点预测评分与真实评分之间误差最小，推荐质量最优。基于用户的协同过滤算法使用较稀疏的评分矩阵计算相似度，所得MAE值最大；对用户属性进行聚类的协同过滤算法在一定程度上使所得目标用户的近邻用户集更准确，所得MAE值较小；而该文对用户进行属性聚类并填充稀疏的评分矩阵，减小数据的稀疏度，所得MAE值在三者中最小。

4 结束语

针对旅游数据稀疏性偏大的问题，对用户属性进行二分k-means聚类，对评分矩阵进行填充，得到完整的用户评分矩阵；在目标用户所在的类别中，对目标用户计算Pearson相似度，找到目标用户的近邻用户集；计算目标用户对未游览景点的预测评分，构成Top-N推荐列表，向目标用户展示。实验表明，该算法的推荐质量优于传统推荐算法。