多项式零点的并行圆盘迭代法研究

努尔麦麦江·阿布都吾甫

(喀什大学 数学与统计学院，新疆 喀什 844000)

求解多项式零点问题是解决很多实际问题的过程中经常要遇到的数学问题之一，也引起了众多人的广泛关注[1]。多项式方程到了5次及其以上就没有公式解，因而对于多项式方程的求解，一般只能用迭代法得到近似解，研究其迭代法尤为必要。章迪平等人通过构建4阶并行迭代方法，实现了多项式重零点的求解，并通过收敛性定理的证明解释了多阶方程快速计算思路[2]。安静等人建立Jacobi多项式及其任意阶导数零点求解方法，通过数值实例证明该方法的实效性[3]。目前多项式方程的迭代法有很多，由于一般的迭代法，在得到近似值时，误差需另外估计。但区间和圆盘算法在得到近似值的同时还给出了误差估计。王秋华等人利用圆盘算法构建多项式并行Halley算法，收敛速度能够达到10阶，极大的拓宽了算法的应用范围[4]。因而本文主要集中讨论区间和圆盘算法，但是其算法对于多项式方程有重根的情形可能失效[5]。本文将在异步并行圆盘迭代法的基础上，对其进行了改进，使它既保留了原算法的优点，而且还是适用于有重根的多项式方程，使之在实际应用中更具有实效性。

1 并行算法基本概念及其分类

1.1 并行算法基本概念

并行算法是使用多个并行处理器实现大数据多次重复计算的手段，并且要求计算必须在一定的时间内同时完成。其相关的性能定义主要包括：

定义1 一个算法的并行度是算法中能用一个运算步并行完成的运算个数。假设算法运算个数为r，利用s个运算步完成，则r/s称为平均并行度。

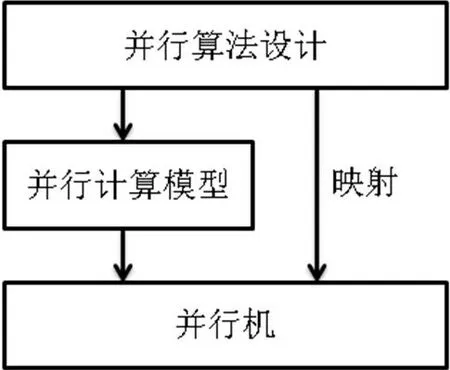
图1 并行计算模型

如图1所示，并行计算有别于串行算法，将并行算法的设计与计算模型映射到并行机上进行运算，大大提高了运算的速度与运算之间的并行度。此外，加速比与效率是对并行算法设计以及并行计算模型构建能效的重要影响因素，通过提升并行算法的加速比使其无限接近SP=P，即并行效率EP=1，从而提升并行机的运算速度。然而，由于并行度、系统负荷、同步时间延长迟等原因，往往无法实现理想状态(加速比SP=P)。因此，需要通过调整并行运算的计算模型结构与算法设计过程，最大限度的降低各种影响因素的负效应，例如异步算法的改进就是提升运算加速比的最直接有效的方法。

1.2 并行算法分类

并行算法的分类比较广泛，通用的分类是根据运算进程是否同步可以分为同步并行算法与异步并行算法[7]。其中，同步并行算法是指存在k个进程的算法同时进行，但是执行过程是按照一个一个进程有序的进行。因此会出现某些进程待机或者计算冗余的情况，而且只能在拥有k台并行机的SIMD系统或MIMD系统中进行运算。而异步并行算法则是需要拥有k台并行机的MIMD系统中进行运算，k个进程执行过程不需要同步，因此在算法上不存在重复运行的情况发生，大大提升了运算的加速比，但是却需要比较复杂的控制指令。此外，异步并行算法在执行k个进程过程中存在转折区间，即当通信变量信息出现问题或者存在冲突的时候可以选择终止或者暂停，实现执行过程的转变以达到后验先趋的运算关系。所以，本文选择灵活性更强的异步并行算法作为研究对象，以满足多项式方程重根求解的需要。

2 多项式方程求根算法的改进

2.1 异步并行圆盘算法

多项式方程求根的算法有很多，包括Laguerre方法，圆盘Schroeder方法，Halley法等。这些算法不仅具有收敛速度快，还具有同时求解零点的特点。下面Halley异步并行算法作简单介绍。

记f(x)=(x-ξi)g(x)，其中f(x)和g(x)均为包含ξi的某个区域上的解析函数，且g(ξi)≠0，记

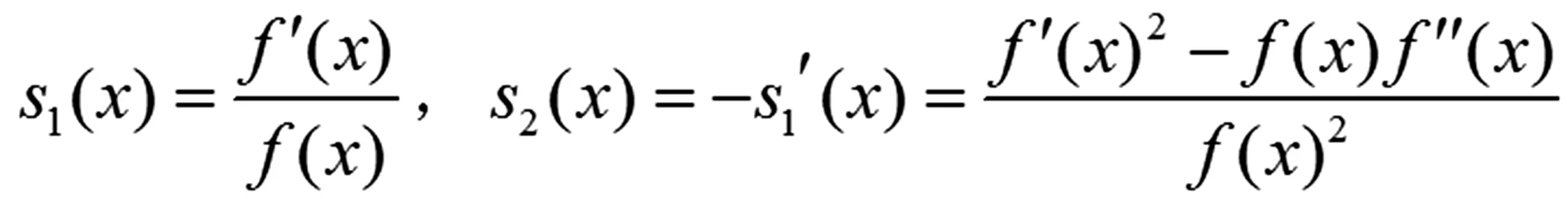
设f(x)是以ξ1,ξ2,…,ξn为全部零点的n次多项式，则

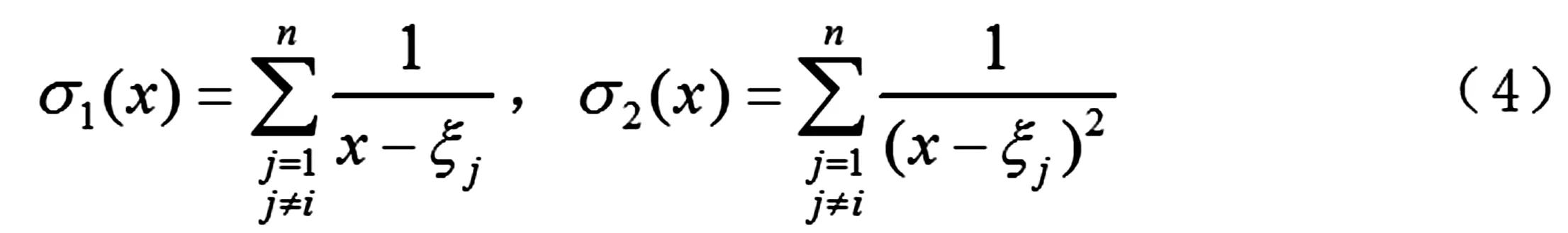
在具体计算时，用

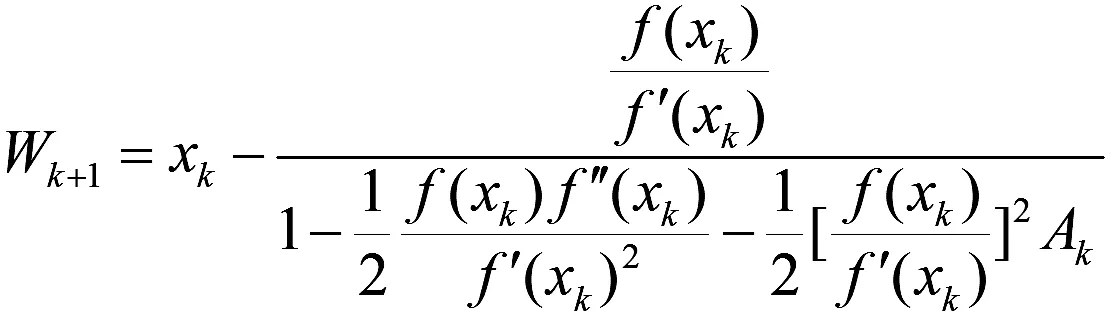
来计算Wk+1可能更方便。由圆盘的四则运算的包含单调性可知，在ξj∈Uk条件下，有ξi∈Wk+1。对于算法(5)，有如下收敛定理。

2.2 改进的圆盘迭代法

通过前文介绍了异步并行圆盘迭代法，它虽然既保持了Halley圆盘迭代法的优点，同时又是异步并行算法，但它并不适用于有重根的情形。因此，后续将对异步并行圆盘迭代法进行改进，在保留该法的原有优点前提下，而且适用于单根或重根的情形。

(6)

(7)

(8)

设f(x)是最高次项系数为1，且以ξm1,ξm2,…,ξml(ln)为全部零点的n次多项式，其中ξi≠ξj(i≠j)，ξi重数为mi(i=1,2,…,l)为正整数，则

(9)

Step1Wk=[xk;rk]；

Step2 若f(xk)=0，则转入Step5；

Step4 若rk+1>ε，则k=k+1，转入Step2，否则转入Step5；

Step5 结束。

在具体计算时，用

来计算Wk+1可能更方便。由圆盘的四则运算的包含单调性可知，在ξj∈Uk条件下，有ξi∈Wk+1。对于算法(10)，有如下收敛定理。

(11)

rk+1

(12)

证明：利用式(7)和式(10)得

(13)

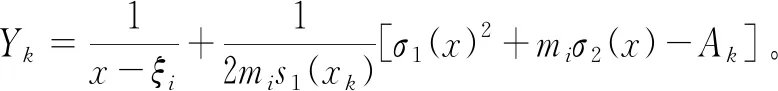
下面分情况证明：

(1)当f(x0)=0时，取x0=x1，r1=0；

(2)当f(x0)≠0时，根据圆盘运算的定义，由x0∉U0得

a0=0

(14)

(15)

则由式(6)，(9)，(14)，(15)得

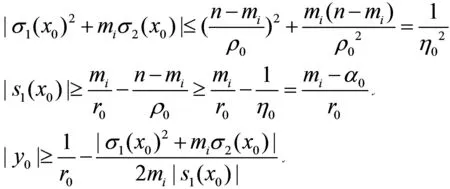
R0

(16)

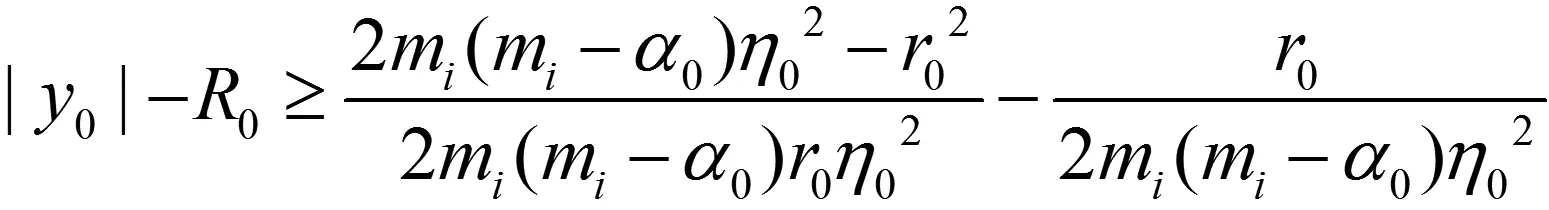
(17)

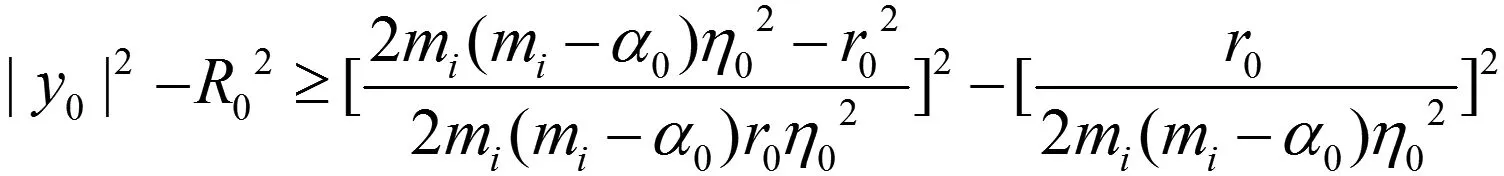
(18)

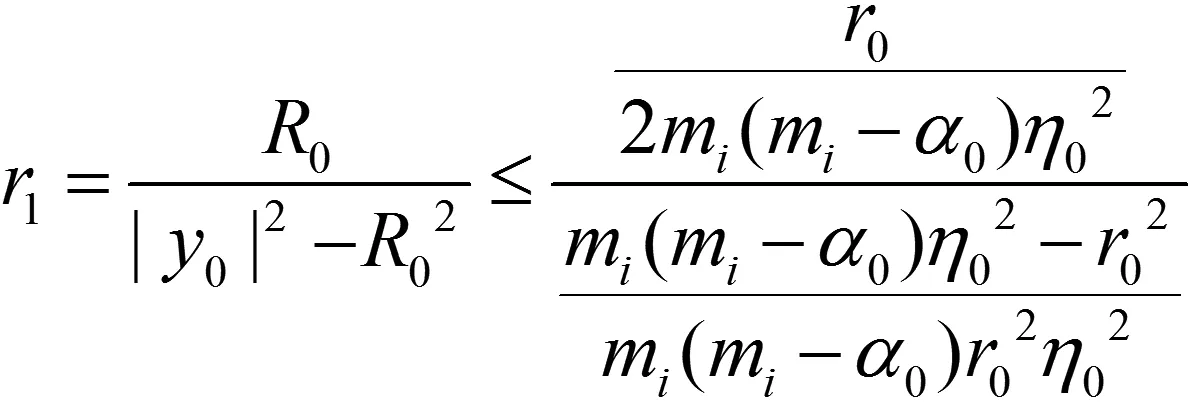
(19)

故有r1即无论f(x)=0还是f(x)≠0，都有

r1

成立。

由式(11)，(19)得

r1

(20)

如能证明ξj∈U1，α1成立，则式(12)对所有的k成立，下面分情况证明它。

(1)当f(x0)=0时，取x0=x1，r1=0，则有

1)由于|ξj-x1|=|ξj-x0|-|x0-x1|≥ρ0-|x0-x1|=ρ1，所以ξj∈U1；

(2)当f(x0)≠0时，证明如下：

由于|ξj-x1|≥|ξj-x0|-|x0-x1|≥ρ0-|x0-x1|=ρ1，所以ξj∈U1。

由式(11)，(13)，(17)得：

(21)

由式(20)，(21)得：

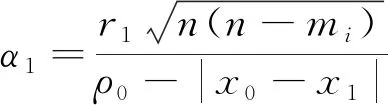
故无论f(x)=0还是f(x)≠0，都有ξj∈U1，α1成立。同时式(12)结果对任意k都成立，且rk+1当k→时，rk→0，而ξi∈Wk，所以定理证明完毕。综上所述，当W0中f(x)有且只有零点ξi，同时f(x)其余零点均在中，W0的半径满足(11)式，则由式(10)产生的圆盘序列至少以3阶的收敛速度收敛于ξi。

3 结论

本文主要针对多项式方程求根时有重根问题进行展开讨论，在现有的异步并行圆盘迭代法基础上，进行改进，构造一种新的圆盘迭代法，使得其算法不仅保持了原算法的优点，而且适用于多项式有重零点的情形，使之在实际应用中更具有实效性。最后讨论了它的收敛性，得出该算法的收敛定理。此外，改进后的迭代法能够适用于存在重根的多项式方程，对于零点的计算具有十分重要的应用意义。